Abstract
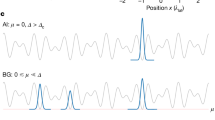
The disordered Bose–Hubbard model—a paradigm for strongly correlated and disordered bosonic systems1—is central to our understanding of quantum phase transitions2. Despite extensive theoretical work on the disordered Bose–Hubbard model, little is known about the impact of temperature, the dynamical behaviour of quantum phases, and how equilibrium is affected during quantum phase transitions. These issues are critically important to applications such as quantum annealing3,4,5,6,7 and electronics based on quantum phase transitions8. Here, we use a quantum quench of disorder in an ultracold lattice gas to dynamically probe the superfluid–Bose glass quantum phase transition at non-zero temperature ( Fig. 1). By measuring excitations generated during the quench, we provide evidence for superfluid puddles in the Bose glass phase and produce a superfluid–Bose glass phase diagram consistent with completely constrained, finite temperature, and equilibrium quantum Monte Carlo simulations. The residual energy from the quench, which is an efficacy measure for optimization through quantum annealing, is unchanged for quench times spanning nearly a hundred tunnelling times.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 12 print issues and online access
$259.00 per year
only $21.58 per issue
Buy this article
- Purchase on SpringerLink
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
References
Fisher, M. P., Weichman, P. B., Grinstein, G. & Fisher, D. S. Boson localization and the superfluid-insulator transition. Phys. Rev. B 40, 546–570 (1989).
Sachdev, S. Quantum Phase Transitions 2nd edn (Cambridge Univ. Press, 2011).
Santoro, G. E., Martonák, R., Tosatti, E. & Car, R. Theory of quantum annealing of an Ising spin glass. Science 295, 2427–2430 (2002).
Santoro, G. E. & Tosatti, E. Optimization using quantum mechanics: quantum annealing through adiabatic evolution. J. Phys. A 39, R393 (2006).
Bian, Z. et al. Discrete optimization using quantum annealing on sparse Ising models. Front. Phys. 2, 56 (2014).
Das, A. & Chakrabarti, B. K. Colloquium: quantum annealing and analog quantum computation. Rev. Mod. Phys. 80, 1061–1081 (2008).
Boixo, S. et al. Evidence for quantum annealing with more than one hundred qubits. Nature Phys. 10, 218–224 (2014).
Yang, Z., Ko, C. & Ramanathan, S. Oxide electronics utilizing ultrafast metal-insulator transitions. Annu. Rev. Mater. Res. 41, 337–367 (2011).
White, M. et al. Strongly interacting bosons in a disordered optical lattice. Phys. Rev. Lett. 102, 055301 (2009).
Pollet, L. A review of Monte Carlo simulations for the Bose–Hubbard model with diagonal disorder. C.R. Phys. 14, 712–724 (2013).
Yao, Z., da Costa, K. P. C., Kiselev, M. & Prokof’ev, N. Critical exponents of the superfluid–Bose-glass transition in three dimensions. Phys. Rev. Lett. 112, 225301 (2014).
Gadway, B., Pertot, D., Reeves, J., Vogt, M. & Schneble, D. Glassy behavior in a binary atomic mixture. Phys. Rev. Lett. 107, 145306 (2011).
Pasienski, M., McKay, D., White, M. & DeMarco, B. A disordered insulator in an optical lattice. Nature Phys. 6, 677–680 (2010).
Fallani, L., Lye, J. E., Guarrera, V., Fort, C. & Inguscio, M. Ultracold atoms in a disordered crystal of light: towards a Bose glass. Phys. Rev. Lett. 98, 130404 (2007).
D’Errico, C. et al. Observation of a disordered bosonic insulator from weak to strong interactions. Phys. Rev. Lett. 113, 095301 (2014).
Zhou, S. Q. & Ceperley, D. M. Construction of localized wave functions for a disordered optical lattice and analysis of the resulting Hubbard model parameters. Phys. Rev. A 81, 013402 (2010).
Chen, D., White, M., Borries, C. & DeMarco, B. Quantum quench of an atomic Mott insulator. Phys. Rev. Lett. 106, 235304 (2011).
Scherer, D. R., Weiler, C. N., Neely, T. W. & Anderson, B. P. Vortex formation by merging of multiple trapped Bose–Einstein condensates. Phys. Rev. Lett. 98, 110402 (2007).
Dziarmaga, J. Dynamics of a quantum phase transition and relaxation to a steady state. Adv. Phys. 59, 1063–1189 (2010).
Braun, S. et al. Emergence of coherence and the dynamics of quantum phase transitions. Proc. Natl Acad. Sci. USA 112, 3641–3646 (2015).
Dziarmaga, J. Dynamics of a quantum phase transition in the random Ising model: logarithmic dependence of the defect density on the transition rate. Phys. Rev. B 74, 064416 (2006).
Caneva, T., Fazio, R. & Santoro, G. E. Adiabatic quantum dynamics of a random Ising chain across its quantum critical point. Phys. Rev. B 76, 144427 (2007).
Brooke, J., Bitko, D., Rosenbaum, T. F. & Aeppli, G. Quantum annealing of a disordered magnet. Science 284, 779–781 (1999).
Pollet, L., Prokof’ev, N., Svistunov, B. & Troyer, M. Absence of a direct superfluid to Mott insulator transition in disordered Bose systems. Phys. Rev. Lett. 103, 140402 (2009).
Leggett, A. J. Quantum liquids: Bose Condensation and Cooper Pairing in Condensed-Matter Systems (Oxford Univ. Press, 2006).
Ray, U. & Ceperley, D. M. Revealing the condensate and noncondensate distributions in the inhomogeneous Bose–Hubbard model. Phys. Rev. A 87, 051603 (2013).
Bissbort, U., Thomale, R. & Hofstetter, W. Stochastic mean-field theory: method and application to the disordered Bose–Hubbard model at finite temperature and speckle disorder. Phys. Rev. A 81, 063643 (2010).
Lin, C.-H., Sensarma, R., Sengupta, K. & Das Sarma, S. Quantum dynamics of disordered bosons in an optical lattice. Phys. Rev. B 86, 214207 (2012).
Lucas, A. Ising formulations of many NP problems. Front. Phys. 2, 5 (2014).
Acknowledgements
The authors acknowledge funding from the National Science Foundation (grants PHY 12-05548 and PHY 15-05468) and the Army Research Office (grant W911NF-12-1-0462). Computation time was provided by XSEDE resources at TACC (Texas) and INCITE resources at Oak Ridge National Laboratory.
Author information
Authors and Affiliations
Contributions
B.D., C.M., U.R. and D.M.C. conceived the research. C.M. and U.R. contributed equally to this work: C.M. conducted and analysed the measurements, and U.R. performed and analysed the numerical simulations. P.R. and D.C. contributed to the measurements and data analysis. B.D. and D.M.C. supervised the experimental and theoretical work, respectively. B.D., U.R. and C.M. wrote the manuscript, which was discussed by and commented on by all authors.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary information
Supplementary information (PDF 1011 kb)
Rights and permissions
About this article
Cite this article
Meldgin, C., Ray, U., Russ, P. et al. Probing the Bose glass–superfluid transition using quantum quenches of disorder. Nature Phys 12, 646–649 (2016). https://doi.org/10.1038/nphys3695
Received:
Accepted:
Published:
Issue date:
DOI: https://doi.org/10.1038/nphys3695
This article is cited by
-
Probing the Possibilities of Ergodicity in the 1D Spin-1/2 XY Chain with Quench Dynamics
Scientific Reports (2020)
-
Localisation of weakly interacting bosons in two dimensions: disorder vs lattice geometry effects
Scientific Reports (2019)
-
Coherent inflationary dynamics for Bose–Einstein condensates crossing a quantum critical point
Nature Physics (2018)
-
Disordered Supersolids in the Extended Bose-Hubbard Model
Scientific Reports (2017)