Abstract
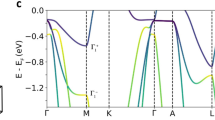
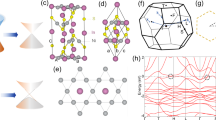
In topological quantum materials1,2,3 the conduction and valence bands are connected at points or along lines in the momentum space. A number of studies have demonstrated that several materials are indeed Dirac/Weyl semimetals4,5,6,7,8. However, there is still no experimental confirmation of materials with line nodes, in which the Dirac nodes form closed loops in the momentum space2,3. Here we report the discovery of a novel topological structure—Dirac node arcs—in the ultrahigh magnetoresistive material PtSn4 using laser-based angle-resolved photoemission spectroscopy data and density functional theory calculations. Unlike the closed loops of line nodes, the Dirac node arc structure arises owing to the surface states and resembles the Dirac dispersion in graphene that is extended along a short line in the momentum space. We propose that this reported Dirac node arc structure is a novel topological state that provides an exciting platform for studying the exotic properties of Dirac fermions.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 12 print issues and online access
$259.00 per year
only $21.58 per issue
Buy this article
- Purchase on SpringerLink
- Instant access to the full article PDF.
USD 39.95
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
Change history
07 April 2016
In the version of this Letter originally published a note about colour figures was mistakenly included in all of the figure captions. These notes have now been removed in all versions of the Letter.
References
Hasan, M. Z. & Kane, C. L. Colloquium: topological insulators. Rev. Mod. Phys. 82, 3045–3067 (2010).
Burkov, A. A., Hook, M. D. & Balents, L. Topological nodal semimetals. Phys. Rev. B 84, 235126 (2011).
Heikkil, T. & Volovik, G. Dimensional crossover in topological matter: evolution of the multiple dirac point in the layered system to the flat band on the surface. JETP Lett. 93, 59–65 (2011).
Liu, Z. K. et al. Discovery of a three-dimensional topological Dirac semimetal, Na3Bi. Science 343, 864–867 (2014).
Neupane, M. et al. Observation of a three-dimensional topological Dirac semimetal phase in high-mobility Cd3As2 . Nature Commun. 5, 3786 (2014).
Xu, S.-Y. et al. Discovery of a Weyl fermion semimetal and topological Fermi arcs. Science 349, 613–617 (2015).
Xu, S. et al. Discovery of a Weyl fermion state with Fermi arcs in niobium arsenide. Nature Phys. 11, 748–754 (2015).
Xu, S.-Y. et al. Experimental discovery of a topological Weyl semimetal state in TaP. Sci. Adv. 1, e1501092 (2015).
Young, S. M. et al. Dirac semimetal in three dimensions. Phys. Rev. Lett. 108, 140405 (2012).
Wang, Z. et al. Dirac semimetal and topological phase transitions in A3Bi (A = Na, K, Rb). Phys. Rev. B 85, 195320 (2012).
Wang, Z., Weng, H., Wu, Q., Dai, X. & Fang, Z. Three-dimensional Dirac semimetal and quantum transport in Cd3As2 . Phys. Rev. B 88, 125427 (2013).
Liu, Z. K. et al. A stable three-dimensional topological Dirac semimetal Cd33As2 . Nature Mater. 13, 677–681 (2014).
Weyl, H. Elektron und gravitation. i. Z. Phys. 56, 330–352 (1929).
Huang, S. et al. A Weyl fermion semimetal with surface Fermi arcs in the transition metal monopnictide TaAs class. Nature Commun. 6, 7373 (2015).
Weng, H., Fang, C., Fang, Z., Bernevig, B. A. & Dai, X. Weyl semimetal phase in noncentrosymmetric transition-metal monophosphides. Phys. Rev. X 5, 011029 (2015).
Weng, H. et al. Topological node-line semimetal in three-dimensional graphene networks. Phys. Rev. B 92, 045108 (2015).
Zeng, M. et al. Topological semimetals and topological insulators in rare earth monopnictides. Preprint at http://arxiv.org/abs/1504.03492 (2015).
Yu, R., Weng, H., Fang, Z., Dai, X. & Hu, X. Topological node-line semimetal and Dirac semimetal state in antiperovskite Cu3PdN. Phys. Rev. Lett. 115, 036807 (2015).
Kim, Y., Wieder, B. J., Kane, C. L. & Rappe, A. M. Dirac line nodes in inversion-symmetric crystals. Phys. Rev. Lett. 115, 036806 (2015).
Fang, C., Chen, Y., Kee, H-Y. & Fu, L. Topological nodal line semimetals with and without spin-orbital coupling. Phys. Rev. B 92, 081201 (2015).
Bian, G. et al. Drumhead surface states and topological nodal-line fermions in TlTaSe2. Preprint at http://arxiv.org/abs/1508.07521 (2015).
Xie, L. S. et al. A new form of Ca3P2 with a ring of Dirac nodes. APL Mater. 3, 083602 (2015).
Yamakage, A., Yamakawa, Y., Tanaka, Y. & Okamoto, Y. Line-node Dirac semimetal and topological insulating phase in noncentrosymmetric pnictides CaAgX (X = P, As). J. Phys. Soc. Jpn 85, 013708 (2016).
Bian, G. et al. Topological nodal-line fermions in spin-orbit metal PbTaSe2 . Nature Commun. 7, 10556 (2016).
Schoop, L. M. et al. Dirac cone protected by non-symmorphic symmetry and 3D Dirac line node in ZrSiS. Preprint at http://arxiv.org/abs/1509.00861 (2015).
Liang, T. et al. Ultrahigh mobility and giant magnetoresistance in the Dirac semimetal Cd3As2 . Nature Mater. 14, 280–284 (2015).
Shekhar, C. et al. Extremely large magnetoresistance and ultrahigh mobility in the topological Weyl semimetal candidate NbP. Nature Phys. 11, 645–649 (2015).
Ali, M. N. et al. Large, non-saturating magnetoresistance in WTe2 . Nature 514, 205–208 (2014).
Mun, E. et al. Magnetic field effects on transport properties of PtSn4 . Phys. Rev. B 85, 035135 (2012).
Wu, Y. et al. Temperature-induced Lifshitz transition in WTe2 . Phys. Rev. Lett. 115, 166602 (2015).
Canfield, P. C. & Fisk, Z. Growth of single crystals from metallic fluxes. Philos. Mag. 65, 1117–1123 (1992).
Canfield, P. C., Kong, T., Kaluarachchi, U. S. & Jo, N. H. Use of frit-disc crucibles for routine and exploratory solution growth of single crystalline samples. Philos. Mag. 96, 84–92 (2016).
Jiang, R. et al. Tunable vacuum ultraviolet laser based spectrometer for angle resolved photoemission spectroscopy. Rev. Sci. Instrum. 85, 033902 (2014).
Hohenberg, P. & Kohn, W. Inhomogeneous electron gas. Phys. Rev. 136, B864–B871 (1964).
Kohn, W. & Sham, L. J. Self-consistent equations including exchange and correlation effects. Phys. Rev. 140, A1133–A1138 (1965).
Kresse, G. & Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 54, 11169–11186 (1996).
Kresse, G. & Furthmller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 6, 15–50 (1996).
Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865–3868 (1996).
Blöchl, P. E. Projector augmented-wave method. Phys. Rev. B 50, 17953–17979 (1994).
Monkhorst, H. J. & Pack, J. D. Special points for Brillouin-zone integrations. Phys. Rev. B 13, 5188–5192 (1976).
Knnen, B., Niepmann, D. & Jeitschko, W. Structure refinements and some properties of the transition metal stannides Os3Sn7, Ir5Sn7, Ni0.402(4)Pd0.598Sn4, α-PdSn2 and PtSn4 . J. Alloys Compd. 309, 1–9 (2000).
Acknowledgements
This work was supported by the US Department of Energy, Office of Science, Basic Energy Sciences, Materials Science and Engineering Division. Ames Laboratory is operated for the US Department of Energy by Iowa State University under contract No. DE-AC02-07CH11358.
Author information
Authors and Affiliations
Contributions
P.C.C. initiated the work by insisting that Y.W. and A.K. design and carry out the experiment. Y.W., D.M. and L.H. acquired and analysed ARPES data. L.-L.W., D.D.J. and Y.L. carried out the DFT calculations. E.M. grew the samples under the supervision of S.L.B. and P.C.C. The manuscript was drafted by Y.W. and A.K. All authors discussed and commented on the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
About this article
Cite this article
Wu, Y., Wang, LL., Mun, E. et al. Dirac node arcs in PtSn4. Nature Phys 12, 667–671 (2016). https://doi.org/10.1038/nphys3712
Received:
Accepted:
Published:
Issue date:
DOI: https://doi.org/10.1038/nphys3712
This article is cited by
-
Comprehensive investigation of quantum oscillations in semimetal using an ac composite magnetoelectric technique with ultrahigh sensitivity
npj Quantum Materials (2024)
-
Engineered interfaces for heterostructured intermetallic nanomaterials
Nature Synthesis (2023)
-
Robust negative longitudinal magnetoresistance and spin–orbit torque in sputtered Pt3Sn and Pt3SnxFe1-x topological semimetal
Nature Communications (2023)
-
Intrinsic surface p-wave superconductivity in layered AuSn4
Nature Communications (2023)
-
Thermodynamic Assessments of the Pd–Sn and Pt–Sn Systems With the Modified Quasi-chemical Model for Liquid
Metallurgical and Materials Transactions A (2022)