Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Letter
  • Published:

Valley-symmetry-preserved transport in ballistic graphene with gate-defined carrier guiding

Nature Physics volume 12, pages 1022–1026 (2016)Cite this article

Subjects

Abstract

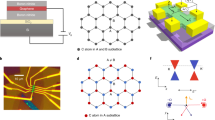
Ever since the discovery of graphene1, valley symmetry and its control2,3 in the material have been a focus of continued studies in relation to valleytronics4,5. Carrier-guiding quasi-one-dimensional (1D) graphene nanoribbons (GNRs)6,7,8,9,10,11,12 with quantized energy subbands preserving the intrinsic Dirac nature have provided an ideal system to that end. Here, by guiding carriers through dual-gate operation in high-mobility monolayer graphene, we report the realization of quantized conductance in steps of 4e2/h in zero magnetic field, which arises from the full symmetry conservation of quasi-1D ballistic GNRs with effective zigzag-edge conduction. A tight-binding model calculation confirms conductance quantization corresponding to zigzag-edge conduction even for arbitrary GNR orientation. Valley-symmetry conservation is further confirmed by intrinsic conductance interference with a preserved Berry phase of π in a graphene-based Aharonov–Bohm (AB) ring prepared by similar dual gating. This top-down approach for gate-defined carrier guiding in ballistic graphene is of particular relevance in the efforts towards efficient and promising valleytronic applications.

Access through your institution
Buy or subscribe

This is a preview of subscription content, access via your institution

Access options

Access through your institution

Buy this article

  • Purchase on SpringerLink
  • Instant access to full article PDF
Buy now

Prices may be subject to local taxes which are calculated during checkout

Figure 1: Gate-defined quasi-1D transport channel built on graphene.
Figure 2: Quantized conductance of a quasi-1D graphene channel in zero magnetic field.
Figure 3: Tight-binding calculations for GNRs with arbitrary axial direction.
Figure 4: Aharonov–Bohm interference in a ballistic graphene device.

Similar content being viewed by others

References

  1. Castro Neto, A. H., Guinea, F., Peres, N. M. R., Novoselov, K. S. & Geim, A. K. The electronic properties of graphene. Rev. Mod. Phys. 81, 109–162 (2009).

    Article  ADS  Google Scholar 

  2. McCann, E. et al. Weak-localization magnetoresistance and valley symmetry in graphene. Phys. Rev. Lett. 97, 146805 (2006).

    Article  ADS  Google Scholar 

  3. Trushin, M. & Schliemann, J. Pseudospin in optical and transport properties of graphene. Phys. Rev. Lett. 107, 156801 (2011).

    Article  ADS  Google Scholar 

  4. Rycerz, A., Tworzydlo, J. & Beenakker, C. W. J. Valley filter and valley valve in graphene. Nature Phys. 3, 172–175 (2007).

    Article  ADS  Google Scholar 

  5. Qiao, Z., Yang, S. A., Wang, B., Yao, Y. & Niu, Q. Spin-polarized and valley helical edge modes in graphene nanoribbons. Phys. Rev. B 84, 035431 (2011).

    Article  ADS  Google Scholar 

  6. Nakada, K., Fujita, M., Dresselhaus, G. & Dresselhaus, M. S. Edge state in graphene ribbons: nanometer size effect and edge shape dependence. Phys. Rev. B 54, 17954–17961 (1996).

    Article  ADS  Google Scholar 

  7. Brey, L. & Fertig, H. A. Electronic states of graphene nanoribbons studied with the Dirac equation. Phys. Rev. B 73, 235411 (2006).

    Article  ADS  Google Scholar 

  8. Peres, N. M. R., Castro Neto, A. H. & Guinea, F. Conductance quantization in mesoscopic graphene. Phys. Rev. B 73, 195411 (2006).

    Article  ADS  Google Scholar 

  9. Akhmerov, A. R. & Beenakker, C. W. J. Boundary conditions for Dirac fermions on a terminated honeycomb lattice. Phys. Rev. B 77, 085423 (2008).

    Article  ADS  Google Scholar 

  10. Li, T. C. & Lu, S.-P. Quantum conductance of graphene nanoribbons with edge defects. Phys. Rev. B 77, 085408 (2008).

    Article  ADS  Google Scholar 

  11. Wurm, J., Wimmer, M. & Richter, K. Symmetries and the conductance of graphene nanoribbons with long-range disorder. Phys. Rev. B 85, 245418 (2012).

    Article  ADS  Google Scholar 

  12. Orlof, A., Ruseckas, J. & Zozoulenko, I. V. Effect of zigzag and armchair edges on the electronic transport in single-layer and bilayer graphene nanoribbons with defects. Phys. Rev. B 88, 125409 (2013).

    Article  ADS  Google Scholar 

  13. Lin, Y.-M., Perebeinos, V., Chen, Z. & Avouris, P. Electrical observation of subband formation in graphene nanoribbons. Phys. Rev. B 78, 161409 (2008).

    Article  ADS  Google Scholar 

  14. Stampfer, C. et al. Energy gaps in etched graphene nanoribbons. Phys. Rev. Lett. 102, 056403 (2009).

    Article  ADS  Google Scholar 

  15. Lian, C. et al. Quantum transport in graphene nanoribbons patterned by metal masks. Appl. Phys. Lett. 96, 103109 (2010).

    Article  ADS  Google Scholar 

  16. Baringhaus, J. et al. Exceptional ballistic transport in epitaxial graphene nanoribbons. Nature 506, 349–354 (2014).

    Article  ADS  Google Scholar 

  17. Tombros, N. et al. Quantized conductance of a suspended graphene nanoconstriction. Nature Phys. 7, 697–700 (2011).

    Article  ADS  Google Scholar 

  18. Goossens, A. M. et al. Gate-defined confinement in bilayer graphene-hexagonal boron nitride hybrid devices. Nano Lett. 12, 4656–4660 (2012).

    Article  ADS  Google Scholar 

  19. Allen, M. T., Martin, J. & Yacoby, A. Gate-defined quantum confinement in suspended bilayer graphene. Nature Commun. 3, 934 (2012).

    Article  ADS  Google Scholar 

  20. Williams, J. R., Low, T., Lundstrom, M. S. & Marcus, C. M. Gate-controlled guiding of electrons in graphene. Nature Nanotech. 6, 222–225 (2011).

    Article  ADS  Google Scholar 

  21. Rickhaus, P. et al. Guiding of electrons in a few-mode ballistic graphene channel. Nano Lett. 15, 5819–5825 (2015).

    Article  ADS  Google Scholar 

  22. Ki, D.-K., Jeong, D., Choi, J.-H., Lee, H.-J. & Park, K.-S. Inelastic scattering in a monolayer graphene sheet: a weak-localization study. Phys. Rev. B 78, 125409 (2008).

    Article  ADS  Google Scholar 

  23. Tikhonenko, F. V., Kozikov, A. A., Savchenko, A. K. & Gorbachev, R. V. Transition between electron localization and antilocalization in graphene. Phys. Rev. Lett. 103, 226801 (2009).

    Article  ADS  Google Scholar 

  24. Wang, L. et al. One-dimensional electrical contact to a two-dimensional material. Science 342, 614–617 (2013).

    Article  ADS  Google Scholar 

  25. Russo, S. et al. Observation of Aharonov–Bohm conductance oscillations in a graphene ring. Phys. Rev. B 77, 085413 (2008).

    Article  ADS  Google Scholar 

  26. Magdalena, H. et al. The Aharonov–Bohm effect in a side-gated graphene ring. New J. Phys. 12, 043054 (2010).

    Article  Google Scholar 

  27. Kim, M. et al. Tuning locality of pair coherence in graphene-based Andreev interferometers. Sci. Rep. 5, 8715 (2015).

    Article  Google Scholar 

  28. van Wees, B. J. et al. Quantized conductance of point contacts in a two-dimensional electron gas. Phys. Rev. Lett. 60, 848–850 (1988).

    Article  ADS  Google Scholar 

  29. Li, T. et al. Effects of dangling ends on the conductance of side-contacted carbon nanotubes. Phys. Rev. B 72, 035422 (2005).

    Article  ADS  Google Scholar 

  30. Beenakker, C. W. J. & van Houten, H. Boundary scattering and weak localization of electrons in a magnetic field. Phys. Rev. B 38, 3232–3240 (1988).

    Article  ADS  Google Scholar 

  31. Liu, G., Velasco, J., Bao, W. & Lau, C. N. Fabrication of graphene p-n-p junctions with contactless top gates. Appl. Phys. Lett. 92, 203103 (2008).

    Article  ADS  Google Scholar 

  32. Giannozzi, P. et al. QUANTUM ESPRESSO: a modular and open-source software project for quantum simulations of materials. J. Phys. Condens. Matter 21, 395502 (2009).

    Article  Google Scholar 

  33. Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865–3868 (1996).

    Article  ADS  Google Scholar 

  34. Marzari, N. & Vanderbilt, D. Maximally localized generalized Wannier functions for composite energy bands. Phys. Rev. B 56, 12847–12865 (1997).

    Article  ADS  Google Scholar 

  35. Charlier, J.-C., Blase, X. & Roche, S. Electronic and transport properties of nanotubes. Rev. Mod. Phys. 79, 677–732 (2007).

    Article  ADS  Google Scholar 

  36. Sancho, M. L., Sancho, J. L. & Rubio, J. Highly convergent schemes for the calculation of bulk and surface Green functions. J. Phys. F 15, 851–858 (1985).

    Article  ADS  Google Scholar 

  37. Hancock, Y., Uppstu, A., Saloriutta, K., Harju, A. & Puska, M. Generalized tight-binding transport model for graphene nanoribbon-based systems. Phys. Rev. B 81, 245402 (2010).

    Article  ADS  Google Scholar 

Download references

Acknowledgements

We would like to thank G.-H. Lee, G.-H. Park, J.-H. Lee and J. Lee for useful discussions on the device fabrication. This work was supported by the National Research Foundation (NRF) through the SRC Center for Topological Matter (Grant No. 2011-0030046 for H.J.L. and Grant No. 2011-0030789 for S.H.J.) and the GFR Center for Advanced Soft Electronics (Grant No. 2014M3A6A5060956).

Author information

Authors and Affiliations

  1. Department of Physics, Pohang University of Science and Technology, Pohang 790-784, Republic of Korea

    Minsoo Kim, Ji-Hae Choi, Sang-Hoon Lee, Seung-Hoon Jhi & Hu-Jong Lee

  2. Advanced Materials Laboratory, National Institute for Materials Science, 1-1 Namiki, Tsukuba 305-0044, Japan

    Kenji Watanabe & Takashi Taniguchi

Authors
  1. Minsoo Kim
    View author publications

    Search author on:PubMed Google Scholar

  2. Ji-Hae Choi
    View author publications

    Search author on:PubMed Google Scholar

  3. Sang-Hoon Lee
    View author publications

    Search author on:PubMed Google Scholar

  4. Kenji Watanabe
    View author publications

    Search author on:PubMed Google Scholar

  5. Takashi Taniguchi
    View author publications

    Search author on:PubMed Google Scholar

  6. Seung-Hoon Jhi
    View author publications

    Search author on:PubMed Google Scholar

  7. Hu-Jong Lee
    View author publications

    Search author on:PubMed Google Scholar

Contributions

M.K. and H.-J.L. conceived the idea and designed the experiments. M.K. prepared the samples and performed measurements. M.K. and H.-J.L. analysed the data. J.-H.C., S.-H.L. and S.-H.J. provided the theoretical consultation and calculation. K.W. and T.T. supplied the high-quality hexagonal boron nitride. H.-J.L. supervised the study. M.K., J.-H.C., S.-H.L., S.-H.J. and H.-J.L. wrote the manuscript. All authors contributed to the discussion and reviewed the manuscript.

Corresponding author

Correspondence to Hu-Jong Lee.

Ethics declarations

Competing interests

The authors declare no competing financial interests.

Supplementary information

Supplementary information

Supplementary information (PDF 2324 kb)

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Kim, M., Choi, JH., Lee, SH. et al. Valley-symmetry-preserved transport in ballistic graphene with gate-defined carrier guiding. Nature Phys 12, 1022–1026 (2016). https://doi.org/10.1038/nphys3804

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue date:

  • DOI: https://doi.org/10.1038/nphys3804

This article is cited by

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing