Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Letter
  • Published:

Acoustic topological insulator and robust one-way sound transport

Nature Physics volume 12, pages 1124–1129 (2016)Cite this article

Subjects

Abstract

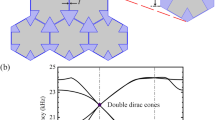
Topological design of materials enables topological symmetries and facilitates unique backscattering-immune wave transport1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26. In airborne acoustics, however, the intrinsic longitudinal nature of sound polarization makes the use of the conventional spin–orbital interaction mechanism impossible for achieving band inversion. The topological gauge flux is then typically introduced with a moving background in theoretical models19,20,21,22. Its practical implementation is a serious challenge, though, due to inherent dynamic instabilities and noise. Here we realize the inversion of acoustic energy bands at a double Dirac cone15,27,28 and provide an experimental demonstration of an acoustic topological insulator. By manipulating the hopping interaction of neighbouring ’atoms’ in this new topological material, we successfully demonstrate the acoustic quantum spin Hall effect, characterized by robust pseudospin-dependent one-way edge sound transport. Our results are promising for the exploration of new routes for experimentally studying topological phenomena and related applications, for example, sound-noise reduction.

Access through your institution
Buy or subscribe

This is a preview of subscription content, access via your institution

Access options

Access through your institution

Buy this article

  • Purchase on SpringerLink
  • Instant access to full article PDF
Buy now

Prices may be subject to local taxes which are calculated during checkout

Figure 1: Schematic of the acoustic insulator and band inversion process.
Figure 2: Acoustic one-way spin-dependent transport.
Figure 3: Robust one-way sound transport.

Similar content being viewed by others

References

  1. Klitzing, K. V., Dorda, G. & Pepper, M. New method for high-accuracy determination of the fine-structure constant based on quantized Hall resistance. Phys. Rev. Lett. 45, 494–497 (1980).

    Article  ADS  Google Scholar 

  2. Thouless, D. J., Kohmoto, M., Nightingale, M. P. & den Nijs, M. Quantized Hall conductance in a two-dimensional periodic potential. Phys. Rev. Lett. 49, 405–408 (1982).

    Article  ADS  Google Scholar 

  3. Hasan, M. Z. & Kane, C. L. Colloquium: topological insulators. Rev. Mod. Phys. 82, 3045–3067 (2010).

    Article  ADS  Google Scholar 

  4. Qi, X.-L. & Zhang, S.-C. Topological insulators and superconductors. Rev. Mod. Phys. 83, 1057–1110 (2011).

    Article  ADS  Google Scholar 

  5. Haldane, F. D. M. & Raghu, S. Possible realization of directional optical waveguides in photonic crystals with broken time-reversal symmetry. Phys. Rev. Lett. 100, 013904 (2008).

    Article  ADS  Google Scholar 

  6. Wang, Z., Chong, Y., Joannopoulos, J. D. & Soljacic, M. Observation of unidirectional backscattering-immune topological electromagnetic states. Nature 461, 772–775 (2009).

    Article  ADS  Google Scholar 

  7. Lu, L., Joannopoulos, J. D. & Soljacic, M. Topological photonics. Nat. Photon. 8, 821–829 (2014).

    Article  ADS  Google Scholar 

  8. Hafezi, M., Demler, E. A., Lukin, M. D. & Taylor, J. M. Robust optical delay lines with topological protection. Nat. Phys. 7, 907–912 (2011).

    Article  Google Scholar 

  9. Hafezi, M., Mittal, S., Fan, J., Migdall, A. & Taylor, J. M. Imaging topological edge states in silicon photonics. Nat. Photon. 7, 1001–1005 (2013).

    Article  ADS  Google Scholar 

  10. Rechtsman, M. C. et al. Photonic floquet topological insulators. Nature 496, 196–200 (2013).

    Article  ADS  Google Scholar 

  11. Khanikaev, A. B. et al. Photonic topological insulators. Nat. Mater. 12, 233–239 (2013).

    Article  ADS  Google Scholar 

  12. Chen, W.-J. et al. Experimental realization of photonic topological insulator in a uniaxial metacrystal waveguide. Nat. Commun. 5, 5782 (2014).

    Article  ADS  Google Scholar 

  13. Lu, L. et al. Experimental observation of Weyl points. Science 349, 622–624 (2015).

    Article  ADS  MathSciNet  Google Scholar 

  14. Bliokh, K. Y., Smirnova, D. & Nori, F. Quantum spin Hall effect of light. Science 348, 1448–1451 (2015).

    Article  ADS  MathSciNet  Google Scholar 

  15. Wu, L.-H. & Hu, X. Scheme for achieving a topological photonic crystal by using dielectric material. Phys. Rev. Lett. 114, 223901 (2015).

    Article  ADS  Google Scholar 

  16. Süsstrunk, R. & Huber, S. D. Observation of phononic helical edge states in a mechanical topological insulator. Science 349, 47–50 (2015).

    Article  ADS  Google Scholar 

  17. Wang, P., Lu, L. & Bertoldi, K. Topological phononic crystals with one-way elastic edge waves. Phys. Rev. Lett. 115, 104302 (2015).

    Article  ADS  Google Scholar 

  18. Mousavi, S. H., Khanikaev, A. B. & Wang, Z. Topologically protected elastic waves in phononic metamaterials. Nat. Commun. 6, 8682 (2015).

    Article  ADS  Google Scholar 

  19. Yang, Z. et al. Topological acoustics. Phys. Rev. Lett. 114, 114301 (2015).

    Article  ADS  Google Scholar 

  20. Ni, X. et al. Topologically protected one-way edge mode in networks of acoustic resonators with circulating air flow. New J. Phys. 17, 053016 (2015).

    Article  ADS  Google Scholar 

  21. Khanikaev, A. B., Fleury, R., Mousavi, S. H. & Alu, A. Topologically robust sound propagation in an angular-momentum-biased graphene-like resonator lattice. Nat. Commun. 6, 8260 (2015).

    Article  ADS  Google Scholar 

  22. Fleury, R., Sounas, D. L., Sieck, C. F., Haberman, M. R. & Alù, A. Sound isolation and giant linear nonreciprocity in a compact acoustic circulator. Science 343, 516–519 (2014).

    Article  ADS  Google Scholar 

  23. Zhu, X.-F. et al. Topologically protected acoustic helical edge states and interface states in strongly coupled metamaterial ring lattices. Preprint at http://arXiv.org/abs/1508.06243 (2015).

  24. Fleury, R., Khanikaev, A. & Alu, A. Floquet topological insulators for sound. Nat. Commun. 7, 11744 (2016).

    Article  ADS  Google Scholar 

  25. Xiao, M. et al. Geometric phase and band inversion in periodic acoustic systems. Nat. Phys. 11, 240–244 (2015).

    Article  Google Scholar 

  26. Xiao, M., Chen, W.-J., He, W.-Y. & Chan, C. T. Synthetic gauge flux and Weyl points in acoustic systems. Nat. Phys. 11, 920–924 (2015).

    Article  Google Scholar 

  27. Chen, Z.-G. et al. Accidental degeneracy of double Dirac cones in a phononic crystal. Sci. Rep. 4, 4613 (2014).

    Article  Google Scholar 

  28. Li, Y., Wu, Y. & Mei, J. Double Dirac cones in phononic crystals. Appl. Phys. Lett. 105, 014107 (2014).

    Article  ADS  Google Scholar 

  29. Ma, T., Khanikaev, A. B., Mousavi, S. H. & Shvets, G. Guiding electromagnetic waves around sharp corners: topologically protected photonic transport in metawaveguides. Phys. Rev. Lett. 114, 127401 (2015).

    Article  ADS  Google Scholar 

  30. He, C. et al. Photonic topological insulator with broken time-reversal symmetry. Proc. Natl Acad. Sci. USA 113, 4924–4928 (2016).

    Article  ADS  Google Scholar 

  31. Sakoda, K. Double Dirac cones in triangular-lattice metamaterials. Opt. Express 20, 9925–9939 (2012).

    Article  ADS  Google Scholar 

  32. Li, Y. & Mei, J. Double Dirac cones in two-dimensional dielectric photonic crystals. Opt. Express 23, 12089–12099 (2015).

    Article  ADS  Google Scholar 

  33. He, C. et al. Tunable one-way cross-waveguide splitter based on gyromagnetic photonic crystal. Appl. Phys. Lett. 96, 111111 (2010).

    Article  ADS  Google Scholar 

  34. Fu, L. Topological crystalline insulators. Phys. Rev. Lett. 106, 106802 (2011).

    Article  ADS  Google Scholar 

  35. He, C., Lu, M.-H., Wan, W.-W., Li, X.-F. & Chen, Y.-F. Influence of boundary conditions on the one-way edge modes in two-dimensional magneto-optical photonic crystals. Solid State Commun. 150, 1976–1979 (2010).

    Article  ADS  Google Scholar 

Download references

Acknowledgements

The work was jointly supported by the National Basic Research Program of China (Grant No. 2012CB921503, 2013CB632904 and 2013CB632702) and the National Nature Science Foundation of China (Grant No. 11134006, No. 11474158, and No. 11404164). M.-H.L. also acknowledges the support of the Natural Science Foundation of Jiangsu Province (BK20140019) and the support from the Academic Program Development of Jiangsu Higher Education (PAPD).

Author information

Authors and Affiliations

  1. National Laboratory of Solid State Microstructures & Department of Materials Science and Engineering, Nanjing University, Nanjing, Jiangsu 210093, China

    Cheng He, Xu Ni, Hao Ge, Xiao-Chen Sun, Yan-Bin Chen, Ming-Hui Lu, Xiao-Ping Liu & Yan-Feng Chen

  2. Collaborative Innovation Center of Advanced Microstructures, Nanjing University, Nanjing, Jiangsu 210093, China

    Cheng He, Ming-Hui Lu, Xiao-Ping Liu & Yan-Feng Chen

Authors
  1. Cheng He
    View author publications

    Search author on:PubMed Google Scholar

  2. Xu Ni
    View author publications

    Search author on:PubMed Google Scholar

  3. Hao Ge
    View author publications

    Search author on:PubMed Google Scholar

  4. Xiao-Chen Sun
    View author publications

    Search author on:PubMed Google Scholar

  5. Yan-Bin Chen
    View author publications

    Search author on:PubMed Google Scholar

  6. Ming-Hui Lu
    View author publications

    Search author on:PubMed Google Scholar

  7. Xiao-Ping Liu
    View author publications

    Search author on:PubMed Google Scholar

  8. Yan-Feng Chen
    View author publications

    Search author on:PubMed Google Scholar

Contributions

C.H., M.-H.L. and X.-P.L. conceived the idea. C.H. performed the numerical simulation and fabricated the samples. C.H., X.N. and H.G. carried out the experimental measurements. All the authors contributed to discussion of the results and manuscript preparation. M.-H.L., X.-P.L. and Y.-F.C. supervised all aspects of this work and managed this project.

Corresponding authors

Correspondence to Ming-Hui Lu, Xiao-Ping Liu or Yan-Feng Chen.

Ethics declarations

Competing interests

The authors declare no competing financial interests.

Supplementary information

Supplementary information

Supplementary information (PDF 2544 kb)

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

He, C., Ni, X., Ge, H. et al. Acoustic topological insulator and robust one-way sound transport. Nature Phys 12, 1124–1129 (2016). https://doi.org/10.1038/nphys3867

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue date:

  • DOI: https://doi.org/10.1038/nphys3867

This article is cited by

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing