Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Letter
  • Published:

Distortion and destruction of colloidal flocks in disordered environments

Nature Physics volume 13, pages 63–67 (2017)Cite this article

Subjects

Abstract

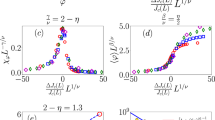
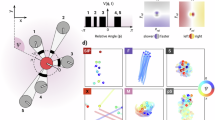
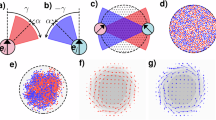
How do flocks, herds and swarms move through disordered environments? The answer to this question is crucial not only to animal groups in the wild, but also to effectively all applications of collective robotics and active materials composed of synthetic motile units1,2,3,4,5,6,7,8,9,10,11,12,13,14. In stark contrast, aside from rare exceptions15,16,17, our physical understanding of flocking has so far been limited to homogeneous media18,19,20. Here we explain how collective motion survives in geometrical disorder. To do so, we combine experiments and analytical theory to examine motile colloids cruising between randomly positioned microfabricated obstacles. We elucidate how disorder and bending elasticity compete to channel the flow of polar flocks along sparse river networks akin those found beyond plastic depinning in driven condensed matter21. Further increasing the disorder, we demonstrate that collective motion is suppressed in the form of a first-order phase transition generic to all polar active materials.

Access through your institution
Buy or subscribe

This is a preview of subscription content, access via your institution

Access options

Access through your institution

Buy this article

  • Purchase on SpringerLink
  • Instant access to full article PDF
Buy now

Prices may be subject to local taxes which are calculated during checkout

Figure 1: Emergence and suppression of collective motion.
Figure 2: Flock morphology.
Figure 3: Flocking through river networks.
Figure 4: Roller–obstacle scattering.

Similar content being viewed by others

References

  1. Kernbach, S. Handbook of Collective Robotics - Fundamentals and Challenges (Pan Stanford Edition, 2013).

    Book  Google Scholar 

  2. Werfel, J., Petersen, K. & Nagpal, R. Designing collective behavior in a termite-inspired robot construction team. Science 343, 754–758 (2014).

    Article  ADS  Google Scholar 

  3. Berman, S., Radhika, N. & Halasz, A. Optimization of stochastic strategies for spatially inhomogeneous robot swarms: a case study in commercial pollination. Proceedings of IEEE/RSJ International Conference on IntelligentRobots and Systems (IROS’11) 3923–3930 (IEEE Computer Society Press, 2011).

    Google Scholar 

  4. Shklarsh, A., Ariel, G., Schneidman, E. & Ben-Jacob, E. Smart swarms of bacteria-inspired agents with performance adaptable interactions. PLoS Comput. Biol. 7, e1002177 (2011).

    Article  ADS  MathSciNet  Google Scholar 

  5. Schaller, V., Weber, C., Semmrich, C., Frey, E. & Bausch, A. Polar patterns of driven filaments. Nature 467, 73–77 (2010).

    Article  ADS  Google Scholar 

  6. Deseigne, J., Dauchot, O. & Chaté, H. Collective motion of vibrated polar disks. Phys. Rev. Lett. 105, 098001 (2010).

    Article  ADS  Google Scholar 

  7. Thutupalli, S., Seemann, R. & Herminghaus, S. Swarming behavior of simple model squirmers. New J. Phys. 13, 073021 (2011).

    Article  ADS  Google Scholar 

  8. Sanchez, T., Chen, D. T. N., DeCamp, S., Heymann, M. & Dogic, Z. Spontaneous motion in hierarchically assembled active matter. Nature 491, 431–435 (2012).

    Article  ADS  Google Scholar 

  9. Theurkauff, I., Cottin-Bizonne, C., Palacci, J., Ybert, C. & Bocquet, L. Dynamic clustering in active colloidal suspensions with chemical signaling. Phys. Rev. Lett. 108, 268303 (2012).

    Article  ADS  Google Scholar 

  10. Bricard, A., Caussin, J.-B., Desreumaux, N., Dauchot, O. & Bartolo, D. Emergence of macroscopic directed motion in populations of motile colloids. Nature 503, 95–98 (2013).

    Article  ADS  Google Scholar 

  11. Palacci, J., Sacanna, S., Steinberg, A. P., Pine, D. J. & Chaikin, P. M. Living crystals of light-activated colloidal surfers. Science 339, 936–940 (2013).

    Article  ADS  Google Scholar 

  12. Buttinoni, I. et al. Dynamical clustering and phase separation in suspensions of self-propelled colloidal particles. Phys. Rev. Lett. 23, 238301 (2013).

    Article  ADS  Google Scholar 

  13. Lushi, E., Wioland, H. & Goldstein, R. E. Fluid flows created by swimming bacteria drive self-organization in confined suspensions. Proc. Natl Acad. Sci. USA 111, 9733–9738 (2014).

    Article  ADS  Google Scholar 

  14. Nishiguchi, D. & Sano, M. Mesoscopic turbulence and local order in Janus particles self-propelling under an ac electric field. Phys. Rev. E 92, 052309 (2015).

    Article  ADS  Google Scholar 

  15. Chepizhko, O., Altmann, E. G. & Peruani, F. Optimal noise maximizes collective motion in heterogeneous media. Phys. Rev. Lett. 110, 238101 (2013).

    Article  ADS  Google Scholar 

  16. Reichhardt, C. & Olson Reichhardt, C. J. Active matter transport and jamming on disordered landscapes. Phys. Rev. E 90, 012701 (2014).

    Article  ADS  Google Scholar 

  17. Quint, D. A. & Gopinathan, A. Topologically induced swarming phase transition on a 2D percolated lattice. Phys. Biol. 12, 046008 (2015).

    Article  ADS  Google Scholar 

  18. Marchetti, M. C. et al. Hydrodynamics of soft active matter. Rev. Mod. Phys. 85, 1143–1189 (2013).

    Article  ADS  Google Scholar 

  19. Vicsek, T. & Zafeiris, A. Collective motion. Phys. Rep. 517, 71–140 (2012).

    Article  ADS  Google Scholar 

  20. Cavagna, A. & Giardina, I. Bird flocks as condensed matter. Annu. Rev. Condens. Matter Phys. 5, 183–207 (2014).

    Article  ADS  Google Scholar 

  21. Reichhardt, C. & Olson, C. J. Depinning and nonequilibrium dynamic phases of particle assemblies driven over random and ordered substrates: a review. Preprint at http://arxiv.org/abs/1602.03798v1 (2016).

  22. Bricard, A. et al. Emergent vortices in populations of colloidal rollers. Nat. Commun. 6, 7470 (2015).

    Article  ADS  Google Scholar 

  23. Quincke, G. Über Rotationen im constanten electrischen Felde. Ann. Phys. 295, 417–486 (1896).

    Article  Google Scholar 

  24. Jensen, H. J., Brass, A. & Berlinsky, A. J. Lattice deformations and plastic flow through bottlenecks in a two-dimensional model for flux pinning in type-II superconductors. Phys. Rev. Lett. 60, 1676–1679 (1988).

    Article  ADS  Google Scholar 

  25. Grønbech-Jensen, N., Bishop, A. R. & Domínguez, D. Metastable filamentary vortex flow in thin film superconductors. Phys. Rev. Lett. 76, 2985–2988 (1996).

    Article  ADS  Google Scholar 

  26. Troyanovski, A. M., Aarts, J. & Kes, P. H. Collective and plastic vortex motion in superconductors at high flux densities. Nature 399, 665–668 (1999).

    Article  ADS  Google Scholar 

  27. Le Doussal, P. & Giamarchi, T. Moving glass theory of driven lattices with disorder. Phys. Rev. B 57, 11356–11403 (1998).

    Article  ADS  Google Scholar 

  28. Faleski, M. C., Marchetti, M. C. & Middleton, A. A. Vortex dynamics and defects in simulated flux flow. Phys. Rev. B 54, 12427–12436 (1996).

    Article  ADS  Google Scholar 

  29. Topinka, M. A. et al. Coherent branched flow in a two-dimensional electron gas. Nature 410, 183–186 (2001).

    Article  ADS  Google Scholar 

  30. Pertsinidis, A. & Ling, X. S. Statics and dynamics of 2D colloidal crystals in a random pinning potential. Phys. Rev. Lett. 100, 028303 (2008).

    Article  ADS  Google Scholar 

  31. Yan, L., Barizien, A. & Wyart, M. A model for the erosion onset of a granular bed sheared by a viscous fluid. Phys. Rev. E 93, 012903 (2015).

    Article  ADS  Google Scholar 

  32. Chepizhko, O. & Peruani, F. Diffusion, subdiffusion, and trapping of active particles in heterogeneous media. Phys. Rev. Lett. 111, 160604 (2013).

    Article  ADS  Google Scholar 

  33. Solon, A. P., Chaté, H. & Tailleur, J. From phase to microphase separation in flocking models: the essential role of nonequilibrium fluctuations. Phys. Rev. Lett. 114, 068101 (2015).

    Article  ADS  Google Scholar 

  34. Vicsek, T., Czirók, A., Ben-Jacob, E., Cohen, I. & Shochet, O. Novel type of phase transition in a system of self-driven particles. Phys. Rev. Lett. 75, 1226–1229 (1995).

    Article  ADS  MathSciNet  Google Scholar 

  35. Grégoire, G. & Chaté, H. Onset of collective and cohesive motion. Phys. Rev. Lett. 92, 025702 (2013).

    Article  ADS  Google Scholar 

  36. Kellerer, A. M. On the number of clumps resulting from the overlap of randomly placed figures in a plane. J. Appl. Probab. 20, 126–135 (1983).

    Article  MathSciNet  Google Scholar 

  37. Crocker, J. C. & Grier, G. Methods of digital video microscopy for colloidal studies. J. Colloid Interface Sci. 179, 298–310 (1996).

    Article  ADS  Google Scholar 

Download references

Acknowledgements

We acknowledge support from ANR program MiTra and Institut Universitaire de France. We thank F. Peruani, S. Santucci, M. C. Marchetti and D. Carpentier for valuable comments and suggestions. We also thank G. Fabre for help with the experiments.

Author information

Authors and Affiliations

  1. Univ. Lyon, Ens de Lyon, Univ. Claude Bernard, CNRS, Laboratoire de Physique, F-69342 Lyon, France

    Alexandre Morin, Nicolas Desreumaux, Jean-Baptiste Caussin & Denis Bartolo

Authors
  1. Alexandre Morin
    View author publications

    Search author on:PubMed Google Scholar

  2. Nicolas Desreumaux
    View author publications

    Search author on:PubMed Google Scholar

  3. Jean-Baptiste Caussin
    View author publications

    Search author on:PubMed Google Scholar

  4. Denis Bartolo
    View author publications

    Search author on:PubMed Google Scholar

Contributions

D.B. conceived the project. N.D., A.M. and D.B. designed the experiments. N.D. and A.M. performed the experiments. J.-B.C. and D.B. performed the theory. N.D., A.M., J.-B.C. and D.B. analysed and discussed results. D.B. and A.M. wrote the paper. N.D. and A.M. have equal contributions.

Corresponding author

Correspondence to Denis Bartolo.

Ethics declarations

Competing interests

The authors declare no competing financial interests.

Supplementary information

Supplementary information

Supplementary information (PDF 1650 kb)

Supplementary Movie 1

Supplementary Movie (MP4 20902 kb)

Supplementary Movie 2

Supplementary Movie (MP4 23891 kb)

Supplementary Movie 3

Supplementary Movie (MP4 20070 kb)

Supplementary Movie 4

Supplementary Movie (MP4 16992 kb)

Supplementary Movie 5

Supplementary Movie (MP4 16112 kb)

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Morin, A., Desreumaux, N., Caussin, JB. et al. Distortion and destruction of colloidal flocks in disordered environments. Nature Phys 13, 63–67 (2017). https://doi.org/10.1038/nphys3903

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue date:

  • DOI: https://doi.org/10.1038/nphys3903

This article is cited by

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing