Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Letter
  • Published:

Unstable fronts and motile structures formed by microrollers

Nature Physics volume 13, pages 375–379 (2017)Cite this article

Subjects

This article has been updated

Abstract

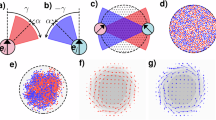
Condensation of objects into stable clusters occurs naturally in equilibrium1 and driven systems2,3,4,5. It is commonly held that potential interactions6, depletion forces7, or sensing8 are the only mechanisms which can create long-lived compact structures. Here we show that persistent motile structures can form spontaneously from hydrodynamic interactions alone, with no sensing or potential interactions. We study this structure formation in a system of colloidal rollers suspended and translating above a floor, using both experiments and large-scale three-dimensional simulations. In this system, clusters originate from a previously unreported fingering instability, where fingers pinch off from an unstable front to form autonomous ‘critters’, whose size is selected by the height of the particles above the floor. These critters are a stable state of the system, move much faster than individual particles, and quickly respond to a changing drive. With speed and direction set by a rotating magnetic field, these active structures offer interesting possibilities for guided transport, flow generation, and mixing at the microscale.

Access through your institution
Buy or subscribe

This is a preview of subscription content, access via your institution

Access options

Access through your institution

Buy this article

  • Purchase on SpringerLink
  • Instant access to full article PDF
Buy now

Prices may be subject to local taxes which are calculated during checkout

Figure 1: Strong velocity enhancement due to collective effects.
Figure 2: Fingering instability.
Figure 3: Self-sustained critters.
Figure 4: Instability and clustering controlled by hydrodynamics.

Similar content being viewed by others

Change history

  • 10 March 2017

    In the version of this Letter orignally published, the Acknowledgements was missing the following sentence: 'We gratefully acknowledge the support of the NVIDIA Corporation with the donation of GPU hardware for performing some of the simulations reported here'. This has been corrected in all versions of this Letter.

References

  1. Anderson, V. J. & Lekkerkerker, H. N. Insights into phase transition kinetics from colloid science. Nature 416, 811–815 (2002).

    Article  ADS  Google Scholar 

  2. Aranson, I. S. & Tsimring, L. S. Patterns and collective behavior in granular media: theoretical concepts. Rev. Mod. Phys. 78, 641–692 (2006).

    Article  ADS  Google Scholar 

  3. Marchetti, M. et al. Hydrodynamics of soft active matter. Rev. Mod. Phys. 85, 1143–1189 (2013).

    Article  ADS  Google Scholar 

  4. Palacci, J., Sacanna, S., Steinberg, A. P., Pine, D. J. & Chaikin, P. M. Living crystals of light-activated colloidal surfers. Science 339, 936–940 (2013).

    Article  ADS  Google Scholar 

  5. Bialké, J., Speck, T. & Löwen, H. Active colloidal suspensions: clustering and phase behavior. J. Non-Cryst. Solids 407, 367–375 (2015).

    Article  ADS  Google Scholar 

  6. Lu, P. J. & Weitz, D. A. Colloidal particles: crystals, glasses, and gels. Annu. Rev. Condens. Matter Phys. 4, 217–233 (2013).

    Article  ADS  Google Scholar 

  7. Schwarz-Linek, J. et al. Phase separation and rotor self-assembly in active particle suspensions. Proc. Natl Acad. Sci. USA 109, 4052–4057 (2012).

    Article  ADS  Google Scholar 

  8. Vicsek, T. & Zafeiris, A. Collective motion. Phys. Rep. 517, 71–140 (2012).

    Article  ADS  Google Scholar 

  9. Blake, J. & Chwang, A. Fundamental singularities of viscous flow. J. Eng. Math. 8, 23–29 (1974).

    Article  Google Scholar 

  10. Lee, S. & Leal, L. Motion of a sphere in the presence of a plane interface. Part 2. an exact solution in bipolar co-ordinates. J. Fluid Mech. 98, 193–224 (1980).

    Article  ADS  Google Scholar 

  11. Huppert, H. E. Flow and instability of a viscous current down a slope. Nature 300, 427–429 (1982).

    Article  ADS  Google Scholar 

  12. Chandrasekhar, S. Hydrodynamic and Hydromagnetic Stability (Oxford, 1961).

    MATH  Google Scholar 

  13. Sacanna, S., Rossi, L. & Pine, D. J. Magnetic click colloidal assembly. J. Am. Chem. Soc. 134, 6112–6115 (2012).

    Article  Google Scholar 

  14. Bricard, A., Caussin, J.-B., Desreumaux, N., Dauchot, O. & Bartolo, D. Emergence of macroscopic directed motion in populations of motile colloids. Nature 503, 95–98 (2013).

    Article  ADS  Google Scholar 

  15. Sing, C. E., Schmid, L., Schneider, M. F., Franke, T. & Alexander-Katz, A. Controlled surface-induced flows from the motion of self-assembled colloidal walkers. Proc. Natl Acad. Sci. USA 107, 535–540 (2010).

    Article  ADS  Google Scholar 

  16. Martinez-Pedrero, F., Ortiz-Ambriz, A., Pagonabarraga, I. & Tierno, P. Colloidal microworms propelling via a cooperative hydrodynamic conveyor belt. Phys. Rev. Lett. 115, 138301 (2015).

    Article  ADS  Google Scholar 

  17. Grzybowski, B. A., Stone, H. A. & Whitesides, G. M. Dynamic self-assembly of magnetized, millimetre-sized objects rotating at a liquid–air interface. Nature 405, 1033–1036 (2000).

    Article  ADS  Google Scholar 

  18. Snezhko, A. Complex collective dynamics of active torque-driven colloids at interfaces. Curr. Opin. Colloid Interface Sci. 21, 65–75 (2016).

    Article  Google Scholar 

  19. Swan, J. W. & Brady, J. F. Simulation of hydrodynamically interacting particles near a no-slip boundary. Phys. Fluids 19, 113306 (2007).

    Article  ADS  Google Scholar 

  20. Usabiaga, F. B. et al. Hydrodynamics of suspensions of passive and active rigid particles: a rigid multiblob approach. Preprint at http://arxiv.org/abs/1602.02170 (2016).

  21. Burgers, J. The Nonlinear Diffusion Equation: Asymptotic Solutions and Statistical Problems. Lecture series (Springer, 1974).

    Book  Google Scholar 

  22. Beatus, T., Tlusty, T. & Bar-Ziv, R. Burgers shock waves and sound in a 2D microfluidic droplets ensemble. Phys. Rev. Lett. 103, 114502 (2009).

    Article  ADS  Google Scholar 

  23. Desreumaux, N., Caussin, J.-B., Jeanneret, R., Lauga, E. & Bartolo, D. Hydrodynamic fluctuations in confined particle-laden fluids. Phys. Rev. Lett. 111, 118301 (2013).

    Article  ADS  Google Scholar 

  24. Goodman, J. & Miller, J. R. Long-time behavior of scalar viscous shock fronts in two dimensions. J. Dyn. Differ. Equ. 11, 255–277 (1999).

    Article  MathSciNet  Google Scholar 

  25. Pouliquen, O., Delour, J. & Savage, S. Fingering in granular flows. Nature 386, 816–817 (1997).

    Article  ADS  Google Scholar 

  26. Pan, T., Joseph, D. & Glowinski, R. Modelling Rayleigh–Taylor instability of a sedimenting suspension of several thousand circular particles in a direct numerical simulation. J. Fluid Mech. 434, 23–37 (2001).

    Article  ADS  Google Scholar 

  27. Lin, T., Rubinstein, S. M., Korchev, A. & Weitz, D. A. Pattern formation of charged particles in an electric field. Langmuir 30, 12119–12123 (2014).

    Article  Google Scholar 

  28. Wysocki, A. et al. Direct observation of hydrodynamic instabilities in a driven non-uniform colloidal dispersion. Soft Matter 5, 1340–1344 (2009).

    Article  ADS  Google Scholar 

  29. Metzger, B., Nicolas, M. & Guazzelli, E. Falling clouds of particles in viscous fluids. J. Fluid Mech. 580, 283–301 (2007).

    Article  ADS  Google Scholar 

  30. Löwen, H. Particle-resolved instabilities in colloidal dispersions. Soft Matter 6, 3133–3142 (2010).

    Article  ADS  Google Scholar 

  31. Guazzelli, E. & Hinch, J. Fluctuations and instability in sedimentation. Annu. Rev. Fluid Mech. 43, 97–116 (2011).

    Article  ADS  MathSciNet  Google Scholar 

  32. Allan, D., Caswell, T., Keim, N. & van der Wel, C. trackpy: Trackpy v0.3.2 [Data set]. Zenodo. https://doi.org/10.5281/zenodo.60550 (2016).

Download references

Acknowledgements

This work was supported primarily by the Gordon and Betty Moore Foundation through Grant GBMF3849 and the Materials Research Science and Engineering Center (MRSEC) program of the National Science Foundation under Award Number DMR-1420073. A. Donev and B. Delmotte were supported in part by the National Science Foundation under award DMS-1418706. P. Chaikin was partially supported by NASA under Grant Number NNX13AR67G. We gratefully acknowledge the support of the NVIDIA Corporation with the donation of GPU hardware for performing some of the simulations reported here.

Author information

Author notes

  1. Michelle Driscoll and Blaise Delmotte: These authors contributed equally to this work.

Authors and Affiliations

  1. Department of Physics, New York University, New York, New York 10003, USA

    Michelle Driscoll & Paul Chaikin

  2. Courant Institute of Mathematical Sciences, New York University, New York, New York 10012, USA

    Blaise Delmotte & Aleksandar Donev

  3. Department of Chemistry, New York University, New York, New York 10003, USA

    Mena Youssef & Stefano Sacanna

Authors
  1. Michelle Driscoll
    View author publications

    Search author on:PubMed Google Scholar

  2. Blaise Delmotte
    View author publications

    Search author on:PubMed Google Scholar

  3. Mena Youssef
    View author publications

    Search author on:PubMed Google Scholar

  4. Stefano Sacanna
    View author publications

    Search author on:PubMed Google Scholar

  5. Aleksandar Donev
    View author publications

    Search author on:PubMed Google Scholar

  6. Paul Chaikin
    View author publications

    Search author on:PubMed Google Scholar

Contributions

M.D. performed the experiments. B.D. performed the simulations. M.Y. and S.S. synthesized the colloidal particles. M.D., B.D., A.D. and P.C. conceived the project, analysed the results and wrote the paper.

Corresponding authors

Correspondence to Michelle Driscoll or Blaise Delmotte.

Ethics declarations

Competing interests

The authors declare no competing financial interests.

Supplementary information

Supplementary information

Supplementary information (PDF 1332 kb)

Supplementary Movie 1

Supplementary Movie (AVI 4730 kb)

Supplementary Movie 2

Supplementary Movie (AVI 4299 kb)

Supplementary Movie 3

Supplementary Movie (AVI 4778 kb)

Supplementary Movie 4

Supplementary Movie (AVI 4449 kb)

Supplementary Movie 5

Supplementary Movie (AVI 3385 kb)

Supplementary Movie 6

Supplementary Movie (AVI 4873 kb)

Supplementary Movie 7

Supplementary Movie (AVI 4638 kb)

Supplementary Movie 8

Supplementary Movie (AVI 4765 kb)

Supplementary Movie 9

Supplementary Movie (AVI 4686 kb)

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Driscoll, M., Delmotte, B., Youssef, M. et al. Unstable fronts and motile structures formed by microrollers. Nature Phys 13, 375–379 (2017). https://doi.org/10.1038/nphys3970

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue date:

  • DOI: https://doi.org/10.1038/nphys3970

This article is cited by

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing