Quantum tricritical points in NbFe₂

Abstract

Quantum critical points (QCPs) emerge when a second-order phase transition is suppressed to zero temperature. In metals the quantum fluctuations at such a QCP can give rise to new phases, including unconventional superconductivity. Whereas antiferromagnetic QCPs have been studied in considerable detail, ferromagnetic (FM) QCPs are much harder to access. In almost all metals FM QCPs are avoided through either a change to first-order transitions or through an intervening spin-density-wave (SDW) phase. Here, we study the prototype of the second case, NbFe₂. We demonstrate that the phase diagram can be modelled using a two-order-parameter theory in which the putative FM QCP is buried within a SDW phase. We establish the presence of quantum tricritical points (QTCPs) at which both the uniform and finite wavevector susceptibility diverge. The universal nature of our model suggests that such QTCPs arise naturally from the interplay between SDW and FM order and exist generically near a buried FM QCP of this type. Our results promote NbFe₂ as the first example of a QTCP, which has been proposed as a key concept in a range of narrow-band metals, including the prominent heavy-fermion compound YbRh₂Si₂.

Main

Transition metal compounds with low-temperature magnetic order offer attractive departure points in the study of correlated electron materials. Key materials such as MnSi, ZrZn₂ or Ni₃Al have been investigated for many years; high-quality and well-characterized single crystals are widely available, their magnetic states have been studied in detail, and their magnetic excitation spectrum and electronic structure are often known from neutron scattering and quantum oscillation measurements. A semi-quantitative understanding of key properties such as the size of the ordered moment, the ordering temperature and the low-temperature heat capacity is achieved within spin-fluctuation theory^1,2. Close to the border of magnetism, however, the predictions of conventional spin-fluctuation theory no longer apply, providing a long-standing fundamental challenge to our understanding of correlated electron systems^3,4. Key discrepancies concern firstly, the low-temperature form of the electrical resistivity ρ(T), which follows a still insufficiently understood T^3/2 power-law temperature dependence on the paramagnetic side of the ferromagnetic (FM) quantum phase transition^5,6,7,8, and secondly, the fate of FM order itself: rather than being continuously suppressed towards a FM quantum critical point (QCP), the FM QCP is avoided in clean metals.

One scenario for the avoidance, by which the FM transition becomes first order near the putative QCP, is well understood by theory and experimentally well established^9,10,11,12. The alternative scenario, namely that the FM QCP is masked—or buried—by emergent modulated magnetic order, has been discussed theoretically^13,14,15,16, but with the exception of early work on NbFe₂ (refs 8,17) and recent studies on LaCrGe₃ (ref. 18), as well as local moment systems PrPtAl (ref. 19), CeRuPO (ref. 20), CeFePO (ref. 21), and YbRh₂Si₂ (ref. 22), this second scenario has so far been little explored experimentally. Many of these materials bear the complication of additional energy scales from interactions between conduction electrons, localized f-electrons, crystal field levels, and complex magnetic order. The transition metal itinerant magnet NbFe₂ avoids these complications and has a simple crystal and magnetic structure.

NbFe₂ can be tuned across a FM quantum phase transition by slight changes in the composition that preserve good crystal quality, as documented by the residual resistivity ratios of our samples. These range between 6 and 15 (see Fig. 1c), close to the clean limit as detailed in Supplementary Information I. The effect of slight Nb or Fe excess at the levels employed is restricted to anti-site substitution, with negligible interstitial defects or vacancies. The good quality of samples across the interesting substitution range enables multi-probe studies of quantum phase transitions without the complications of high pressure⁸. Whereas Nb_1−yFe_2+y orders ferromagnetically at low temperature for modest levels of iron excess y > 0.01, stoichiometric or Nb-rich Nb_1−yFe_2+y has long been known to exhibit signatures of a further magnetic phase transition^17,23,24,25, which has recently been proven by microscopic probes to tip the system into incommensurate long-wavelength spin-density-wave (SDW) order with finite wavevector Q oriented along the crystallographic c direction throughout the SDW phase^26,27. The SDW transition temperature extrapolates smoothly to zero for y ≃ −0.015, and near this SDW QCP, the heat capacity Sommerfeld coefficient exhibits a logarithmic temperature dependence, whereas ρ(T) follows a T^3/2 power-law form⁸. These prior findings strongly support the long-standing proposal¹⁷ that a FM QCP is indeed buried within an emergent SDW phase in NbFe₂, and motivate a closer investigation. Here, we present detailed magnetic, electric transport and thermal expansion data collected in newly available high-quality single crystals of the Nb_1−yFe_2+y system at key compositions in the phase diagram. We show that our data are consistent with a two-order-parameter Landau theory²⁸, which provides a novel and convenient framework for extracting three robust findings, namely that the avoided FM QCP can be located accurately inside the emergent SDW dome, that the presence of SDW order causes the FM transition to become first order, and that quantum tricritical points (QTCPs) emerge at finite field. Both SDW and FM fluctuations associated with the FM QTCPs will contribute to the excitation spectrum near the SDW QCP, which may explain the seemingly contradictory temperature dependencies of the heat capacity and resistivity in NbFe₂ mentioned above. Thus, our results provide new routes towards understanding the enigmatic physics of materials at the border of ferromagnetism.

Figure 1: Magnetic transitions in Nb_1−yFe_2+y in zero magnetic field.

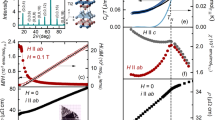
a–c, Temperature dependence of the real part of the c -axis a.c. magnetic susceptibility χ′ (T) (a), the c-axis linear thermal expansion d(ΔL/L₀)/dT (b), and of the electrical resistivity ρ(T) (c) and its temperature derivative dρ/dT (inset in c) for Nb_1−yFe_2+y with y = 0.015 and y = 0. Vertical black arrows indicate the transitions at T_c and T_N. Red and blue arrows in a indicate the measurements taken on warming and cooling, respectively. a.u., arbitrary units.

Results

Our high-quality single crystals show the previously established variation of the FM and SDW phases in a set of zero-field measurements (Fig. 1). In iron-rich Nb_0.985Fe_2.015 signatures of both FM and SDW transitions are seen at T_c ≃ 24 K and T_N ≃ 32 K, respectively as anomalies in the temperature-dependent a.c. magnetic susceptibility χ(T), linear thermal expansion d(ΔL/L₀)/dT and electrical resistivity ρ(T). These signatures are consistent with first- and second-order transitions at T_c and T_N, respectively: the peak in χ(T) shows hysteresis at T_c only, the thermal expansion shows a peak at T_c and a kink at T_N, and the resistivity has a distinct kink at T_c with hysteresis (Supplementary Fig. 2), but only a much weaker anomaly is present in the derivative dρ/dT at T_N. The FM state is unambiguously identified by remanent magnetization (see below).

Stoichiometric NbFe₂ displays a single transition at T_N = 12 K with the characteristics of SDW order: a peak in χ(T) without hysteresis, a kink in d(ΔL/L₀)/dT, and a weak enhancement in dρ/dT above the linear background from higher temperatures (Fig. 1). Similarly, for niobium-rich Nb_1.01Fe_1.99, a single transition consistent with SDW order at T_N = 3 K can be inferred from the peak in χ(T) in Fig. 1a.

The H–T phase diagram is mapped for field parallel to the magnetic axis (H ∥ c) using magnetic susceptibility χ(T, H) measurements for a series of Nb_1−yFe_2+y samples spanning the range from the FM ground state via samples with the SDW ground state to those in ultimate proximity to the SDW QCP (Fig. 2). In iron-rich Nb_0.985Fe_2.015 the maxima in χ(T) signalling the first-order (T_c) and second-order (T_N) transition shift to higher and lower temperature, respectively, for increasing magnetic field. The two signatures approach each other and eventually merge at a critical field μ₀H^⋆ ≃ 0.06 T and a critical temperature T^⋆ ≃ 28 K. Only weak maxima reminiscent of crossovers are observed in χ(T) for fields above H^⋆. Thus, the two lines of anomalies enclose the SDW phase which exists in the small parameter space between T_N and T_c and for fields H ≤ H^⋆ only. At the critical point (H^⋆, T^⋆), the susceptibility reaches peak values comparable to those observed in band ferromagnets with a second-order transition near the Curie temperature, such as ZrZn₂, if slight inhomogeneity and demagnetizing fields are present. We will later see that this enhanced susceptibility is expected within our model of competing order parameters and marks the tricritical point at the transition from first order to second order at T^⋆ (ref. 29). The first- and second-order nature of the low-temperature and high-temperature boundary of the SDW phase can be inferred from the presence and absence of hysteresis in the a.c. susceptibility and electrical resistivity as detailed in Supplementary Information II.

Figure 2: Temperature–magnetic field phase diagrams for the composition series Nb_1−yFe_2+y.

a–c, Colour representation of the real part of the a.c. magnetic susceptibility χ′(H, T) as a function of magnetic field and temperature for iron-rich Nb_0.985 Fe_2.015 (a), stoichiometric NbFe₂ (b) and niobium-rich Nb_1.01Fe_1.99 (c). Points represent positions of the χ′(T) maxima with hysteresis (closed triangles) and without hysteresis (open squares) associated with T_N as well as of the maximum in zero field (open circle) associated with T_c (see text). d, The transition in NbFe₂ at 3 K is identified as first order through the large imaginary part of the susceptibility χ′′(H, T). Solid line in d marks the same phase boundary as in b.

In stoichiometric NbFe₂ the second-order transition can similarly be followed through the H–T phase diagram: the maximum in χ(T) associated with T_N is shifted to lower temperatures upon increasing the magnetic field up to a critical field of 0.45 T. The line of anomalies separates out the low-temperature, low-field part of the H–T phase diagram and suggests that in this region NbFe₂ forms a distinct broken-symmetry state. This ‘cap’ for the SDW phase is reminiscent of the upper part of the SDW phase in iron-rich Nb_0.985Fe_2.015. In fact, we show below that the same competing order parameter model applies to both compositions and the phase diagram of stoichiometric NbFe₂ resembles that of iron-rich Nb_0.985Fe_2.015 with the temperature axis shifted down by approximately 20 K.

Whilst the SDW transition remains second order in NbFe₂ for most of the phase boundary, we find signatures of a tricritical point at (H^⋆ = 0.44 T, T^⋆ = 3 K). Here, the susceptibility is strongly enhanced (Fig. 2b and Supplementary Fig. 3) and a strong signal in the imaginary part χ′′(H^⋆, T^⋆) is observed (Fig. 2d) like in iron-rich Nb_0.985Fe_2.015 at the tricritical point (see Supplementary Information II).

Discussion

Identifying the lines of anomalies for T < T^∗ as phase boundaries is uncontroversial, because they are associated with hysteresis. The case for a second-order ‘cap’ linking the tricritical points at (±H^⋆, T^⋆), however, needs to be examined carefully and resembles the situation in Sr₃Ru₂O₇ at high magnetic field. There, proof of a broken-symmetry state (as opposed to metamagnetic transition lines ending in critical endpoints) came from thermal expansion and thermodynamic data³⁰. In NbFe₂, further to earlier heat capacity measurements on polycrystals¹⁷, strong support for the interpretation of the anomalies at T_N as phase transition anomalies is provided by the thermal expansion measurements (Fig. 1b) and by the recent direct observation of the SDW order in neutron scattering²⁷, as well as indirect evidence from electron spin resonance and muon spin rotation²⁶.

Having established the presence of both the SDW and FM phase transitions we seek a consistent description of the low-temperature phase diagram of Nb_1−yFe_2+y taking into account the proximity to both orders. At the most elementary level, this is done by postulating a Landau expansion of the free energy in terms of two order parameters²⁸:

Here, M denotes the uniform magnetization, which couples linearly to the applied magnetic field, whereas P denotes a general further order parameter, which does not couple directly to the applied field but has a biquadratic coupling to the uniform magnetization. We associate the further order parameter P with the SDW phase. The phenomenological parameters a and b can be extracted directly from magnetization measurements, for example a = χ⁻¹ for M = 0, but the remaining parameters α, β and η are more difficult to obtain. The theory can be formulated in terms of scalar order parameters in isotropic materials, because the more complicated coupling terms in a vector theory will constrain M and P either to point in the same direction or at right angles to each other²⁸. In anisotropic materials, the situation is more complicated, but as long as the field points along the easy axis, as is the case for our studies of Nb_1−yFe_2+y here, the scalar description remains adequate.

In zero field the global free energy minima will correspond to either a paramagnetic state M = P = 0, or one of the possible magnetic states M = 0, P ≠ 0, M ≠ 0, P = 0 or M ≠ 0, P ≠ 0, depending on the parameters {a, b, α, β, η}. All prior observations in polycrystalline NbFe₂, as well as our data on single crystals suggest that for H = 0 the mixed phase M ≠ 0, P ≠ 0 does not occur in NbFe₂, and that on cooling the system will always first develop the SDW order parameter (P ≠ 0), before that is replaced by a uniform magnetization. This constrains α(T) to go through zero at a higher temperature than a(T). The expected phase diagram for this case is illustrated in Fig. 3.

Figure 3: Schematic phase diagram based on the model free energy in equation (1), as applied to Nb_1−yFe_2+y.

Solid blue and red lines indicate the first-order phase boundaries of the SDW and FM phase. Dashed red lines indicate the second-order phase boundary of the SDW phase at high temperatures. Orange circles mark the tricritical points. Horizontal grey dashed lines indicate zero temperature assigned to the different samples of the composition series Nb_1−y Fe_2+y.

We start by comparing the theoretical phase diagram with the observed behaviour in zero field: for H = 0 and within the P ≠ 0 state the free energy has its global minimum at F_P = −α²/(4β) for P² = −α/β. However, if the system were to order uniformly, that is, M ≠ 0, the free energy would have a minimum of F_M = −a²/(4b) at M² = −a/b, and so a first-order transition from the M = 0, P ≠ 0 into the M ≠ 0, P = 0 state will occur at a temperature T_c, below which a²/b > α²/β. This sequence of a second-order transition into the SDW state followed by a first-order transition into the FM state exactly matches our observations in iron-rich Nb_0.985Fe_2.015.

We now turn to the behaviour at finite field. This is conveniently analysed by comparing theoretical and experimental Arrott plots of M² versus H/M. Outside the SDW phase we have

allowing us to extract a(T) as well as b(T) as the intercept and slope, respectively. Inside the SDW phase, that is, for P ≠ 0, the equation of state becomes H = (a + ηP²)M + bM³, while at the same time minimizing the free energy with respect to P gives P² = −(α/β) − (η/β)M². Substituting this into the equation of state results in a modified expression for the Arrott plot within the SDW phase.

Thus, we expect a different slope and intercept in the SDW phase, with a^⋆(T) bifurcating from a(T) and b^⋆(T) changing discontinuously at T_N.

In Fig. 4b, f, and Supplementary Fig. 4 we analyse the high- and low-field parts of the Arrott plots for NbFe₂ and Nb_0.985Fe_2.015 according to equations (2) and (3). Indeed, the slope b^⋆(T) extracted from the low-field part of the Arrott plot changes discontinuously from a positive value b^⋆ = b outside the SDW phase to a negative value b^⋆ ≠ b inside the SDW phase (see Supplementary Information III for more details). The temperature dependence of the extracted parameters in Fig. 4c, d, g, h agrees with the expectations for a Landau theory for NbFe₂, Nb_0.985Fe_2.015, and Nb_1.01Fe_1.99 (not shown): b remains positive at all temperatures, a has a strong temperature dependence, a and a^⋆ bifurcate at T_N, and b^⋆ changes discontinuously at T_N.

Figure 4: Two-order-parameter analysis of the magnetization in Nb_1−yFe_2+y.

a–h, Magnetization isotherms in iron-rich Nb_0.985 Fe_2.015 (a) and stoichiometric NbFe₂ (e) for fields along the crystallographic c-direction. High- and low-field straight-line fits to the Arrott plots of H/M versus M² (b,f) give intercepts a, a^⋆ and slopes b, b^⋆ for Nb_0.985Fe_2.015 (c,d) and NbFe₂ (g,h), enabling a direct comparison with a two-order-parameter Landau theory (see text).

The high-field Arrott-plot intercept a(T) (Fig. 4c, g) crosses through zero at an intermediate temperature T₀ < T_N, which indicates the underlying ferromagnetic instability. Ferromagnetism does not set in at T₀, because it has been preempted by SDW order at T_N, but instead a first-order ferromagnetic transition occurs at a lower temperature T_c < T₀.

Considering next the shape of M(H) isotherms on crossing the SDW phase boundary at constant T yields two regimes within the two-order-parameter model (equations (2) and (3)) (ref. 28). At low temperatures M(H) is predicted to evolve discontinuously through the phase boundary whereas at high temperatures M(H) is expected to evolve continuously. This implies that the phase boundary between the SDW state and the finite field paramagnetic state is expected to be first order and second order at low and high temperatures, respectively, with the two regimes separated by a tricritical point of divergent uniform susceptibility at the maximum critical field of the SDW phase (see Fig. 3). This separation into a first- and second-order regime of the SDW phase boundary entirely matches our observations in iron-rich Nb_0.985Fe_2.015 including the presence of a tricritical point with strongly enhanced susceptibility as discussed above (Fig. 2). Neutron scattering results²⁷ are consistent with this picture. Moreover, they show that the ordering wavevector Q depends only weakly on temperature throughout the SDW phase, and thus make scenarios extremely unlikely by which Q goes continuously to zero at the SDW phase boundary.

Depending on composition, different parts of the schematic phase diagram (Fig. 3) are accessible: in Nb_1.01Fe_1.99, only the top part of the SDW phase is observed, whereas in NbFe₂ the tricritical point is exposed, with a cut-off just below T^⋆. The Clausius–Clapeyron equation dictates that the first-order phase lines intersect the temperature axis with infinite slope in this case. Finally, all aspects of the schematic phase diagram are realized in Fe-rich Nb_0.985Fe_2.015.

Our findings are summarized in the global H–T–y phase diagram in Fig. 5, which illustrates that the accessible part of the schematic phase diagram (Fig. 3) shrinks with increasing Nb content. The global phase diagram also shows the decrease of T₀ as the composition is varied from Fe-rich towards Nb-rich, and that T₀ extrapolates to zero temperature at y ≈ −0.004 and H = 0. This marks the avoided FM QCP buried inside a dome formed by the SDW phase. The intrinsic tendency of clean metallic systems to avoid a FM QCP either by changing the nature of the phase transition from second order to first order or by developing competing SDW magnetic order has long been noted^4,13,15,31. Our observation of emergent SDW order enveloping the preempted FM QCP represents the first example of the latter scenario among itinerant magnets, complementing the recent report of emergent helical order in the local moment system PrPtAl¹⁹.

Figure 5: Overall composition–magnetic field–temperature phase diagram for the Nb_1−yFe_2+y system.

The underlying ferromagnetic transition temperature T₀ is extracted from a(T₀) = 0 (see Fig. 4c, g). The phase boundaries of the SDW and FM phase are obtained from the magnetization and susceptibility measurements as shown in Figs 1–4. The position of the avoided ferromagnetic QCP (blue ball) and the QTCPs (orange ball) are highlighted.

In addition to the buried FM QCP, the global phase diagram (Fig. 5) reveals another important insight, the presence of quantum tricritical points (QTCPs): finite-temperature tricritical points have been located for iron-rich Nb_0.985Fe_2.015 at T^⋆ ≈ 28 K and for stoichiometric NbFe₂ at T^⋆ ≈ 3 K. This demonstrates that the tricritical points can be suppressed to zero temperature, leading to QTCPs. Based on a smooth extrapolation we estimate the location of the QTCPs at (y ≃ −0.003, ±μ₀H ≃ 0.5 T, T = 0).

A divergent uniform susceptibility is not only expected within the two-order-parameter description above²⁸ but also within a self-consistent spin-fluctuation theory for antiferromagnetic order in itinerant systems³². In either case the divergent uniform susceptibility near the QTCP causes strong FM fluctuations. Our preliminary analysis of the uniform susceptibility in Supplementary Information IV does indeed find a divergence χ ∝ Tⁿ with an exponent different from the classical Curie form. Rather the observedexponent of n = 0.79(3) is close to the exponent n = 3/4 expected from spin-fluctuation theory³². The strong FM fluctuations associated with the QTCP may also contribute to the logarithmic divergence of the specific heat observed near the zero-field SDW QCP at (y ≃ −0.01, H = 0, T = 0) (ref. 8). Indeed, recent theoretical work suggests that the finite-temperature behaviour at an SDW QCP may be dominated by FM fluctuations of a nearby FM QCP above a crossover temperature that is different for different physical quantities³³. In NbFe₂, we have a QTCP with FM fluctuations. At the nearby SDW QCP these FM fluctuations can produce C/T ∝ log(T) above a low-lying crossover temperature specific to the heat capacity, whereas the corresponding crossover for resistivity may be higher, such that the signatures of the SDW QCP are retained in ρ(T) at low T.

Analysing our experimental results in newly available single crystals of the band magnet NbFe₂ and its iron-rich composition series in terms of a simple but powerful two-order-parameter Landau theory has brought to light a new generic phase diagram for the vicinity of the FM QCP in clean metallic systems: the FM QCP is enveloped by a dome of emergent SDW order, divergent uniform susceptibility is shifted to tricritical points at finite field, and the line of tricritical points terminates at finite field at zero temperature, generating a QTCP. The coincidence of multiple phase boundaries and critical points may underlie the experimental observation that C/T follows the log(T) behaviour characteristic of a FM QCP, whereas ρ(T) displays the T^3/2 power law expected near an SDW QCP⁸.

The identification of generic QTCPs in NbFe₂ opens up the new phenomenon of quantum tricriticality for experimental studies in a whole class of systems with buried or avoided FM QCP. This provides a fresh perspective on other materials with the same universality, including prototypical heavy-fermion materials^32,34, in which multiple and competing low-energy scales have in the past prevented the detection of a QTCP and obscured the investigation of its consequences.

Methods

Samples from the composition series Nb_1−yFe_2+y with −0.005 < y < 0.015 were grown in an adapted, ultrahigh-vacuum-compatible mirror furnace from polycrystalline ingots prepared by radiofrequency induction melting, as described previously³⁵. The Nb_1.01Fe_1.99 crystal is the same as in ref. 8. Single-crystal grains were selected and oriented by X-ray and neutron diffraction. Magnetic and resistivity measurements were carried out on a Quantum Design PPMS. Thermal expansion measurements made use of a custom-designed dilatometry insert for the PPMS³⁶.

Data availability.

All data needed to evaluate the conclusions in the paper are present in the paper, the Supplementary Methods and the Data repository at the University of Cambridge and can be downloaded from https://dx.doi.org/10.17863/CAM.12354. Additional data related to this paper may be requested from the authors.