Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Letter
  • Published:

Efficient tomography of a quantum many-body system

Nature Physics volume 13, pages 1158–1162 (2017)Cite this article

Subjects

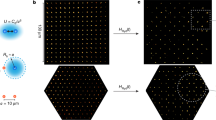
Abstract

Quantum state tomography is the standard technique for estimating the quantum state of small systems1. But its application to larger systems soon becomes impractical as the required resources scale exponentially with the size. Therefore, considerable effort is dedicated to the development of new characterization tools for quantum many-body states2,3,4,5,6,7,8,9,10,11. Here we demonstrate matrix product state tomography2, which is theoretically proven to allow for the efficient and accurate estimation of a broad class of quantum states. We use this technique to reconstruct the dynamical state of a trapped-ion quantum simulator comprising up to 14 entangled and individually controlled spins: a size far beyond the practical limits of quantum state tomography. Our results reveal the dynamical growth of entanglement and describe its complexity as correlations spread out during a quench: a necessary condition for future demonstrations of better-than-classical performance. Matrix product state tomography should therefore find widespread use in the study of large quantum many-body systems and the benchmarking and verification of quantum simulators and computers.

Access through your institution
Buy or subscribe

This is a preview of subscription content, access via your institution

Access options

Access through your institution

Buy this article

  • Purchase on SpringerLink
  • Instant access to full article PDF
Buy now

Prices may be subject to local taxes which are calculated during checkout

Figure 1: Generation and efficient characterization of locally correlated quantum states.
Figure 2: Local measurement results for an 8-spin system quench.
Figure 3: MPS tomography results for an 8-spin quench.
Figure 4: MPS tomography results for a 14-spin quench.

Similar content being viewed by others

References

  1. Vogel, K. & Risken, H. Determination of quasiprobability distributions in terms of probability distributions for the rotated quadrature phase. Phys. Rev. A 40, 2847–2849 (1989).

    Article  ADS  Google Scholar 

  2. Cramer, M. et al. Efficient quantum state tomography. Nat. Commun. 1, 149 (2010).

    Article  ADS  Google Scholar 

  3. Gross, D., Liu, Y.-K., Flammia, S. T., Becker, S. & Eisert, J. Quantum state tomography via compressed sensing. Phys. Rev. Lett. 105, 150401 (2010).

    Article  ADS  Google Scholar 

  4. Flammia, S. T. & Liu, Y.-K. Direct fidelity estimation from few Pauli measurements. Phys. Rev. Lett. 106, 230501 (2011).

    Article  ADS  Google Scholar 

  5. da Silva, M. P., Landon-Cardinal, O. & Poulin, D. Practical characterization of quantum devices without tomography. Phys. Rev. Lett. 107, 210404 (2011).

    Article  ADS  Google Scholar 

  6. Baumgratz, T., Gross, D., Cramer, M. & Plenio, M. B. Scalable reconstruction of density matrices. Phys. Rev. Lett. 111, 020401 (2013).

    Article  ADS  Google Scholar 

  7. Baumgratz, T., Nüßeler, A., Cramer, M. & Plenio, M. B. A scalable maximum likelihood method for quantum state tomography. New J. Phys. 15, 125004 (2013).

    Article  ADS  Google Scholar 

  8. Tóth, G. et al. Permutationally invariant quantum tomography. Phys. Rev. Lett. 105, 250403 (2010).

    Article  ADS  Google Scholar 

  9. Cramer, M. et al. Spatial entanglement of bosons in optical lattices. Nat. Commun. 4, 2161 (2013).

    Article  ADS  Google Scholar 

  10. Shabani, A. et al. Efficient measurement of quantum dynamics via compressive sensing. Phys. Rev. Lett. 106, 100401 (2011).

    Article  ADS  Google Scholar 

  11. Steffens, A. et al. Towards experimental quantum-field tomography with ultracold atoms. Nat. Commun. 6, 7663 (2015).

    Article  ADS  Google Scholar 

  12. Schollwöck, U. The density-matrix renormalization group in the age of matrix product states. Ann. Phys. 326, 96–192 (2011).

    Article  ADS  MathSciNet  Google Scholar 

  13. Fannes, M., Nachtergaele, B. & Werner, R. F. Finitely correlated states on quantum spin chains. Commun. Math. Phys. 144, 443–490 (1992).

    Article  ADS  MathSciNet  Google Scholar 

  14. Hastings, M. B. Solving gapped Hamiltonians locally. Phys. Rev. B 73, 085115 (2006).

    Article  ADS  Google Scholar 

  15. Brandao, F. G. S. L. & Horodecki, M. An area law for entanglement from exponential decay of correlations. Nat. Phys. 9, 721–726 (2013).

    Article  Google Scholar 

  16. Lieb, E. & Robinson, D. The finite group velocity of quantum spin systems. Commun. Math. Phys. 28, 251–257 (1972).

    Article  ADS  MathSciNet  Google Scholar 

  17. Nachtergaele, B. & Sims, R. Much ado about something: why Lieb–Robinson bounds are useful. IAMP News Bull. 4, 22–29 (2010).

    Google Scholar 

  18. Cheneau, M. et al. Light-cone-like spreading of correlations in a quantum many-body system. Nature 481, 484–487 (2012).

    Article  ADS  Google Scholar 

  19. Brandão, F. G. S. L. & Horodecki, M. Exponential decay of correlations implies area law. Commun. Math. Phys. 333, 761–798 (2015).

    Article  ADS  MathSciNet  Google Scholar 

  20. Kim, I. H. On the informational completeness of local observables. Preprint at http://arXiv.org/abs/1405.0137v1 (2014).

  21. Eisert, J. & Osborne, T. J. General entanglement scaling laws from time evolution. Phys. Rev. Lett. 97, 150404 (2006).

    Article  ADS  MathSciNet  Google Scholar 

  22. Bravyi, S., Hastings, M. B. & Verstraete, F. Lieb–Robinson bounds and the generation of correlations and topological quantum order. Phys. Rev. Lett. 97, 050401 (2006).

    Article  ADS  Google Scholar 

  23. Jurcevic, P. et al. Quasiparticle engineering and entanglement propagation in a quantum many-body system. Nature 511, 202–205 (2014).

    Article  ADS  Google Scholar 

  24. Jurcevic, P. et al. Spectroscopy of interacting quasiparticles in trapped ions. Phys. Rev. Lett. 115, 100501 (2015).

    Article  ADS  Google Scholar 

  25. Hauke, P. & Tagliacozzo, L. Spread of correlations in long-range interacting quantum systems. Phys. Rev. Lett. 111, 207202 (2013).

    Article  ADS  Google Scholar 

  26. Haffner, H. et al. Scalable multiparticle entanglement of trapped ions. Nature 438, 643–646 (2005).

    Article  ADS  Google Scholar 

  27. Schachenmayer, J., Lanyon, B. P., Roos, C. F. & Daley, A. J. Entanglement growth in quench dynamics with variable range interactions. Phys. Rev. X 3, 031015 (2013).

    Google Scholar 

  28. Richerme, P. et al. Non-local propagation of correlations in quantum systems with long-range interactions. Nature 511, 198–201 (2014).

    Article  ADS  Google Scholar 

  29. Schindler, P. et al. A quantum information processor with trapped ions. New J. Phys. 15, 123012 (2013).

    Article  ADS  Google Scholar 

  30. Sidje, R. B. A software package for computing matrix exponentials. ACM Trans. Math. Softw. 24, 130–156 (1998).

    Article  Google Scholar 

  31. Jones, E., Oliphant, T. & Peterson, P. et al. SciPy: Open Source Scientific tools for Python (2001); http://www.scipy.org

  32. Ježek, M., Fiurášek, J. & Hradil, Z. Quantum inference of states and processes. Phys. Rev. A 68, 012305 (2003).

    Article  ADS  MathSciNet  Google Scholar 

  33. Plenio, M. B. Logarithmic negativity: a full entanglement monotone that is not convex. Phys. Rev. Lett. 95, 090503 (2005).

    Article  ADS  Google Scholar 

  34. Sabín, C. & García-Alcaine, G. A classification of entanglement in three-qubit systems. Eur. Phys. J. D 48, 435–442 (2008).

    Article  ADS  MathSciNet  Google Scholar 

  35. Perez-Garcia, D., Verstraete, F., Wolf, M. M. & Cirac, J. I. Matrix product state representations. Quantum Inf. Comput. 7, 401–430 (2007).

    MathSciNet  MATH  Google Scholar 

  36. Baumgratz, T. Efficient System Identification and Characterization for Quantum Many-body Systems PhD thesis, Ulm University (2014).

  37. Nielsen, M. A. & Chuang, I. L. Quantum Computation and Quantum Information 9th edn (Cambridge Univ. Press, 2007).

    MATH  Google Scholar 

  38. Osborne, T. J. Efficient approximation of the dynamics of one-dimensional quantum spin systems. Phys. Rev. Lett. 97, 157202 (2006).

    Article  ADS  Google Scholar 

Download references

Acknowledgements

Work in Innsbruck was supported by the Austrian Science Fund (FWF) under the grant number P25354-N20, by the European Commission via the integrated project SIQS, by the Institut für Quanteninformation GmbH and by the US Army Research Office through grant W911NF-14-1-0103. All statements of fact, opinion or conclusions contained herein are those of the authors and should not be construed as representing the official views or policies of ARO, the ODNI, or the US Government. We thank H. Shen and T. Brydges for experimental support in the final stage of the experiment. Work in Ulm was supported by an Alexander von Humboldt Professorship, the ERC Synergy grant BioQ, the EU projects QUCHIP and EQUAM, the US Army Research Office Grant No. W91-1NF-14-1-0133 and the BMBF Verbundproject QuOReP. Numerical computations have been supported by the state of Baden-Württemberg through bwHPC and the German Research Foundation (DFG) through grant no INST 40/467-1 FUGG. I.D. acknowledges support from the Alexander von Humboldt Foundation. M.H. acknowledges contributions from D. Suess to jointly developed code used for data analysis. Work at Strathclyde is supported by the European Union Horizon 2020 collaborative project QuProCS (grant agreement 641277), and by AFOSR grant FA9550-12-1-0057. M.C. acknowledges the ERC grant QFTCMPS and SIQS, the cluster of excellence EXC201 Quantum Engineering and Space-Time Research, and the DFG SFB 1227 (DQ-mat). T.B. acknowledges EPSRC (EP/K04057X/2) and the UK National Quantum Technologies Programme (EP/M01326X/1). B.P.L. acknowledges support by the START prize of the Austrian FWF project Y 849-N20.

Author information

Author notes

  1. B. P. Lanyon and C. Maier: These authors contributed equally to this work.

Authors and Affiliations

  1. Institut für Quantenoptik und Quanteninformation, Österreichische Akademie der Wissenschaften, Technikerstr. 21A, 6020 Innsbruck, Austria

    B. P. Lanyon, C. Maier, P. Jurcevic, R. Blatt & C. F. Roos

  2. Institut für Experimentalphysik, Universität Innsbruck, Technikerstr. 25, 6020 Innsbruck, Austria

    B. P. Lanyon, C. Maier, C. Hempel, P. Jurcevic, R. Blatt & C. F. Roos

  3. Institut für Theoretische Physik and IQST, Albert-Einstein-Allee 11, Universität Ulm, 89069 Ulm, Germany

    M. Holzäpfel, T. Baumgratz, I. Dhand, M. Cramer & M. B. Plenio

  4. Department of Physics, Clarendon Laboratory, University of Oxford, Oxford OX1 3PU, UK

    T. Baumgratz

  5. Department of Physics, University of Warwick, Coventry CV4 7AL, UK

    T. Baumgratz

  6. ARC Centre for Engineered Quantum Systems, School of Physics, The University of Sydney, Sydney, New South Wales, 2006, Australia

    C. Hempel

  7. Department of Physics and SUPA, University of Strathclyde, Glasgow G4 0NG, UK

    A. S. Buyskikh & A. J. Daley

  8. Institut für Theoretische Physik, Leibniz Universität Hannover, 30167 Hannover, Germany

    M. Cramer

Authors
  1. B. P. Lanyon
    View author publications

    Search author on:PubMed Google Scholar

  2. C. Maier
    View author publications

    Search author on:PubMed Google Scholar

  3. M. Holzäpfel
    View author publications

    Search author on:PubMed Google Scholar

  4. T. Baumgratz
    View author publications

    Search author on:PubMed Google Scholar

  5. C. Hempel
    View author publications

    Search author on:PubMed Google Scholar

  6. P. Jurcevic
    View author publications

    Search author on:PubMed Google Scholar

  7. I. Dhand
    View author publications

    Search author on:PubMed Google Scholar

  8. A. S. Buyskikh
    View author publications

    Search author on:PubMed Google Scholar

  9. A. J. Daley
    View author publications

    Search author on:PubMed Google Scholar

  10. M. Cramer
    View author publications

    Search author on:PubMed Google Scholar

  11. M. B. Plenio
    View author publications

    Search author on:PubMed Google Scholar

  12. R. Blatt
    View author publications

    Search author on:PubMed Google Scholar

  13. C. F. Roos
    View author publications

    Search author on:PubMed Google Scholar

Contributions

B.P.L., C.F.R., M.B.P. and M.C. developed and supervised the project; C.M., C.H., B.P.L., P.J., R.B. and C.F.R. performed and contributed to the experiments; B.P.L., M.H., T.B., C.M., C.F.R., I.D., A.S.B. and A.J.D. performed data analysis and modelling; B.P.L. wrote the manuscript, with contributions from all authors.

Corresponding authors

Correspondence to B. P. Lanyon, M. B. Plenio or C. F. Roos.

Ethics declarations

Competing interests

The authors declare no competing financial interests.

Supplementary information

Supplementary information

Supplementary information (PDF 997 kb)

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Lanyon, B., Maier, C., Holzäpfel, M. et al. Efficient tomography of a quantum many-body system. Nature Phys 13, 1158–1162 (2017). https://doi.org/10.1038/nphys4244

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue date:

  • DOI: https://doi.org/10.1038/nphys4244

This article is cited by

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing