Tunable refraction and reflection of self-confined light beams

Abstract

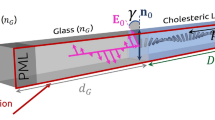
Light filaments or optical spatial solitons are self-confined (non-spreading) beams that originate from the balance between diffraction and self-focusing in nonlinear optical media (those with a response dependent on the level of excitation)^1,2,3. Owing to their ability to self-trap as well as to guide weaker signals (even if differing in colour or modulation format) within the waveguides or ‘light-pipes’ they induce, optical spatial solitons could form the basis of future all-optical processing networks^4,5. One of the most interesting challenges in soliton propagation and engineering concerns light filaments incident on linear/nonlinear or nonlinear/nonlinear interfaces. Here we report the robust propagation, refraction and reflection of optical spatial solitons at the interface between two regions of a nematic liquid crystal. The ability to independently tune the optical properties of each region enables us to steer the beams by refraction and total internal reflection by as much as −18 and +22 degrees, respectively. Moreover, the extended (nonlocal) and anisotropic response of our system supports polarization healing of the solitons across the interface as well as non-specular filament reflection. Finally, exploiting the inherent and all-optically tunable birefringence, we demonstrate unprecedented nonlinear Goos–Hänchen lateral shifts in excess of 0.5 mm.