Abstract
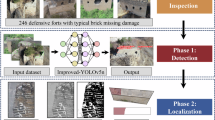
In this paper, a deep learning-based method is proposed for the fast and high-precision detection and digital reconstruction of damaged areas in grotto murals. First, the YOLO Mural breakage detection algorithm is presented, which is based on the YOLOv10 algorithm. The algorithm enhances the backbone network structure through the incorporation of a Star Block module and the parameter-free attention mechanism, SimAM. This modification aims to improve the capture of subtle mural damage features, thereby enhancing the detection precision. In addition, an Efficient-RepGFPN feature fusion network is implemented. The fusion of low-level features with high-level semantic information enabled the model to extract richer feature information. Additionally, the loss function is optimized through the adoption of Inner-SIoU, which allows the model to focus more on locating damaged areas to enhance precision. The AOT-GAN generative adversarial network is utilized to digitally reconstruct the damaged sections of the grotto murals. The experimental results show that the YOLO Mural model has a detection precision of 72.7%, a recall rate of 60.1%, mAP@0.5 of 63.7%, a harmonic mean of 66%, and a real-time detection speed of 289.32 frames per second. Compared to YOLOv10, the YOLO Mural model exhibited a precision increase of 4.15 percentage points and a recall increase of 10.68 percentage points. In comparison with RT-DETR, YOLO v9, YOLO v8, and YOLO v7 models, the YOLO Mural model has the fewest number of parameters, only 2.65 million. When applied to grotto mural restoration, the AOT-GAN model exhibited a PSNR and SSIM of 34.842 and 0.9832, respectively, providing an important reference for subsequent restoration work and potentially saving a significant amount of labor costs.
Similar content being viewed by others
Introduction
As precious parts of the global cultural heritage, grotto murals are treasures of Chinese ancient civilization and art in China. However, owing to complex changes in the natural environment and damage caused by human factors, murals in grottoes generally suffer from degrees of cracks, scratches, peeling, and other forms of degradation in varying degrees1. The development of technology tools that support the damage detection, protection, and restoration of grotto murals is an important aspect of cultural relic protection2,3.
Grotto murals exhibit a variety of damage patterns, ranging from tiny cracks to large areas of detachment, with a wide range of damage types and degrees. This diversity places high demands on the generalization ability of detection algorithms4. Second, the environment in which the murals are located is complex, and variable factors, such as lighting conditions, reflections, and shadows on the surface of the murals, affect the quality of the images obtained and the precision of detection algorithms. In addition, the damaged areas of grotto murals often do not differ significantly from the surrounding intact areas in terms of texture and color, which makes it difficult for models to distinguish between damaged and undamaged areas. Moreover, owing to the fact that the murals may have been created over the span of several centuries, there may be multiple materials and pigment layers on their surfaces, all of which can interfere with damage detection and repair5,6.
With the continuous development of intelligent detection and restoration technologies, non-contact nondestructive analysis of cultural relics using computer vision technology7 has gradually become a focus of current research. In terms of grotto mural damage detection, classical target detection models such as Faster R-CNN8, SSD9, RT-DETR10, and YOLO11,12,13,14,15 have been widely used in the field of cultural heritage protection. Wu16 proposed a lightweight neural network and a multiple attention mechanism method to detect minor cracks, peeling, and other damage effectively. However, the detection speed of the algorithm was only 97.56 fps. Gao17 improved the YOLOv8 algorithm by adding a diverse branch block to improve the detection results for different sizes of Jiangnan private garden’s mural targets. The mAP0.5 reaches 57.1%, but its algorithm suffers from serious leakage of detection for small targets. Wu et al.18 targeted small cracks and defects in grotto murals, proposing an improved loss function based on the one from the YOLOv5 algorithm to accelerate convergence during training. Damage detection precision was improved by 1.29%.
Similarly, cutting-edge research in mural restoration, digitization of artifacts, and computer vision technologies is being conducted in several countries. Spanish frescoes19 were restored through reversibility testing. The frescoes were reintegrated into the irregular surface of the vaults of the Church of San Juan in Valencia (Spain) through 3D digital technology20. Original decoration of the entrance space of a residential building in eastern Galicia during the half-leaf21. With the rapid development of deep learning methods, the shortcomings of traditional methods for image restoration of cave frescoes have been compensated by data-driven approaches22. In order to overcome the difficulties of digital reconstruction of ancient frescoes due to aging, wear, and retouching over time, Merizzi23 used a deep image prior (DIP) restoration method, which computes appropriate reconstructions by relying on the incremental updating of an untrained convolutional neural network, enabling the restoration of highly damaged digital images of medieval paintings in several churches situated in the Mediterranean Alpine Arc. restoration. Chen Yong24 used multilevel feature fusion and hypergraphia convolution for reconstruction, and achieved a clearer and more natural digital reconstruction effect in the Dunhuang grotto murals using antagonistic generation with the SN-PatchGAN discriminator. Aswath et al. 25. proposed CharGAN, an unconditional single image generation model for mural text images. In the proposed system, augmented images are generated from single images using generative adversarial networks while maintaining their structure. Specifically, external enhancement inducers are used to create higher-level enhancements in the generated images.
It can be seen that the effect of damage detection and digital reconstruction of grotto murals through computer vision is remarkable, but there is generally model redundancy, low precision, large computational loads, and the high cost of manual restoration of the existing grotto murals, the complexity of the framework, arithmetic power, while the recreation of the colors is often not sufficiently accurate, resulting in low-quality results. To solve these problems, an efficient method for damage detection and digital reconstruction of grotto murals is proposed. The innovative points are as follows:
First, the SimAM module is integrated into a state-of-the-art convolutional neural network to improve the efficacy of algorithmic detection without introducing additional parameters.
Second, the Efficient-RepGFPN feature fusion network is adopted to enable improved feature focus for grotto mural breakage detection.
Third, the loss function adopts Inner-SIoU, which favors comprehensive performance in the detection algorithms.
Fourth, the AOT-GAN is used to ensure the rationality of the reconstructed image and to improve the filling quality for large missing parts.
Methods
YOLO Mural: grotto mural damage detection algorithm
Currently, the YOLO family of algorithms has become the main approach in the field of single-stage real-time target detection, as they achieve a balance between the computational cost and detection performance. YOLOv10 is the latest version of YOLO algorithms, which is based on the previous generations of YOLO algorithms. YOLOv10 proposes novel multilabel assignment strategies to eliminate NMS operations, improve detection speed, and reduce hyperparameter effects. Some comprehensive and efficient strategies have been designed to improve the precision and real-time performance of the model, including the design of lightweight classification heads and spatial channel separation downsampling. Therefore, in this study, YOLOv10 is selected as the basic algorithm model for grotto mural damage detection.
StarBlock-SimAM module
Star Net26 fuses different subspace features through element-level multiplication, achieving excellent performance and low latency using a compact network structure and a reduced computational load. Star Net contains the StarBlock module, which maps inputs to a high-dimensional nonlinear feature space through star operations; the latter is similar to polynomial kernel functions, where each layer leads to an exponential increase in implicit dimensional complexity. If applied using several layers, star operations can reach nearly infinite dimensions in a compact feature space. Star Net’s simple structure and excellent performance show that its strong representational power stems from the leveraging of the implicit high-dimensional space. This method eliminates the need for deeper networks and wider networks and can play a key role in spatial feature extraction through its improved utilization of computational resources to reduce overhead and improve performance.
Meanwhile, SimAM27 is a lightweight attention mechanism. Compared to existing channel modules and spatial attention modules, the SimAM module does not need to add parameters to the original network but rather infers 3D weights in the feature map. In this study, the SimAM attention mechanism is integrated with StarBlock to generate the Star Block-SimAM module, the schematic of which is shown in Fig. 1.
As shown in Fig. 1, since all neurons in each channel follow the same distribution law, the mean and variance can be calculated first based on the input features in the H and W dimensions. A linear layer, rather than a dot product, is used to calculate the attention weights. The SimAM module automatically assigns different attention levels to the target spatial and channel features without increasing the number of parameters. This suppresses the background features effectively, improving the model’s robustness to interference and enhancing its detection precision. The energy function of the SimAM attention module for evaluating the importance of different neurons is expressed in Eq. (1). In addition, when the energy value of neurons is low, the difference between neurons is greater and more important.
where t denotes the target neuron; μ is the mean of all neurons except t; a is the variance of all neurons except t; λ is a hyperparameter; et denotes the sum of the energy function e across all channels, and spatial dimensions; and X and x are the features after enhancement and before input, respectively. To address the problem of lack of information and similar structures of small targets in grotto mural damage detection, SimAM, which is a 3D parameter-free attention module, is integrated with StarBlock, as it not only reduces the number of network parameters but also enhances its ability to focus on smaller targets.
Efficient-RepGFPN feature fusion network
Conventional FPNs fuse multi-scale features through a top-down path but at a high computational cost. On the other hand, the GFPN achieves better performance by fully exchanging high-level semantic and low-level spatial information. However, GFPN features of different scales share a unified channel and introduce numerous additional up- and down-sampling operations. The Efficient-RepGFPN variant28 is shown in Fig. 2. It adopts different scale feature maps for feature fusion, and different channel dimensions are set to constrain the computational cost and capture image features at different scales efficiently. In addition, to ensure real-time detection, the additional up-sampling operation is removed for more efficient feature fusion and processing.
As shown in Fig. 2, the Fusion Block is the main feature fusion module of the Efficient-RepGFPN network. In the first step, a conventional concatenation operation is performed on the input feature map, and then channel dimensionality reduction is realized using 1 × 1 convolution. Subsequently, multiple Rep 3 × 3 are applied, while 3 × 3 convolutions are also used to perform feature transformations at the output of multiple layers. Feature fusion is eventually accomplished through a concatenation operation. After the feature map output from the backbone network is fed into the Efficient-RepGFPN for fusion, more flexibility and nonlinear expressiveness can be introduced to improve the network’s recognition of the broken elements of the grotto murals, which in turn improves the recognition precision of the model.
Inner-SIoU loss function optimization
The existing loss functions accelerate convergence by adding new loss terms and do not overcome the limitations of the loU itself. Inner-SIoU (linear spatial intersection over union)29 calculates the IoU using an auxiliary bounding box to enhance the network’s generalization ability, as shown in Eq. (3), and uses the scale factor ratio to control the size of the auxiliary bounding box30.
Here, bgt and b are the ground truth and anchor frames, respectively; xc and yc denote the x and y coordinate values of the center point of the frame, respectively; and w and h denote the height and width values of the frame, respectively. ratio corresponds to the scale factor, which is usually within the range of [0.5, 1.5].
The inner SIoU is defined as shown in Eq. (6). The corner vertices of the auxiliary detection frame can be obtained through the application of a transformation to the center point of the detection frame, and the corresponding transformations are applied to both the predicted and real frames of the model output.
When the ratio is one, the auxiliary bezel size is equal to the actual bezel size. The value range of the Inner SIoU loss is [0, 1]. The auxiliary and actual bezels differ only in scale, and the loss function is calculated in the same way. Compared with IoU loss, when the ratio is smaller than 1, the auxiliary border size is smaller than the actual border, so the effective range of regression is smaller than the IoU loss. However, the absolute value of its gradient is larger than the gradient obtained from the IoU loss, which can accelerate the convergence for samples with high IoU. When the ratio is larger than 1, the auxiliary border of the larger scale enlarges the effective range of regression, which is beneficial for the regression of samples with a low IoU.
As shown in Fig. 3, Inner-SIoU calculates the margins between the auxiliary borders and the actual borders. When the auxiliary borders are smaller than the actual borders, the effective range of the regression is smaller than the border loss. However, the absolute value of the gradient is larger than that obtained from the leakage loss, which accelerates the convergence of high-leakage samples. If the auxiliary borders are larger than the actual borders, expanding the effective range of the regression is beneficial for low-leakage cases. Optimizing the loss function in the field of target detection has a relatively small impact on model precision but can improve the recall rate of the detected target effectively; therefore, appropriate tuning of the loss function is beneficial for improving the comprehensive performance of the model.
YOLO Mural: an algorithm for detecting damage to grotto murals
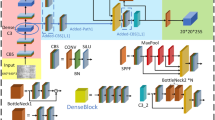
The YOLOv10 model has shown impressive performance when it comes to grotto mural damage detection tasks26, but there is still room for improvement. The structure of the proposed YOLO Mural model is illustrated in Fig. 4.
CBS is convolution + normalization + activation function, StarBlock-SimAM module is an innovative residual module, SCDown is spatial channel decoupling downsampling module, SPPF is a module for feature extraction, and PSA is a large kernel convolution and partial self-attention module. UPSample is an up-sampling module, Concat is a feature connection module, and Efficient RepGFPN is the feature fusion module.
Based on the YOLOv8 algorithm, the model’s innovative features include the spatial channel decoupled down-sampling module (SCDown) and the large kernel convolution and partial self-attention module PSA (Position-wise Spatial Attention) in the feature-extraction stage. However, when dealing with complex textures and breakage patterns of grotto murals, this module may miss key information owing to factors such as occlusion and uneven illumination. Therefore, a StarBlock-SimAM module incorporating the SimAM attention mechanism is incorporated into the feature extraction network to enhance the model’s ability to capture details.
Image input after multiple convolution and batch normalization of SiLU activation functions. When fusing multi-scale feature information, the CIBC2f (Conditional Identity Block) module that introduces the compact inverted block structure is foregone, and the Efficient-RepGFPN feature fusion network is used to compensate for the loss of information after strengthening the multi-layer convolution. This results in a richer gradient information flow and improves the model’s generalization ability. Finally, the results are output at large, medium and small scales. In addition, considering the diversity and irregularity of the broken regions of the mural, the loss function is optimized to reduce edge losses and prediction errors.
Repair of damage to grotto murals
The reconstruction of images of archeological and historical relics refers to filling the missing or damaged parts of the images with realistic content. Currently, generative adversarial networks (GANs) have made great progress in efforts to reconstruct images of broken grotto murals. However, when the missing regions are large, the localized nature of the convolution operation, which does not take into account global or distant structural information but only expands the local receptive field, leads to the distorted structures and blurred textures commonly encountered when most existing restoration methods are applied.
Generative adversarial network
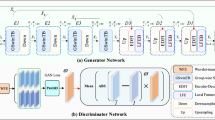
To overcome the above problems, the Aggregated Contextual-Transformation GAN (AOT-GAN)31 has been proposed, which leverages long-range information effectively to enhance the realism of the restored image and improve the quality of the large missing part fillings.
The AOT-GAN’s adversarial network uses aggregated context-feature transformations mainly designed to aggregate multi-scale contextual features to enhance the capture of long-range features and rich structural details. Furthermore, tailored mask prediction is used to enhance the discriminator’s ability to distinguish the generated part from the original image part. The introduction of these design features results in a significant improvement in the quality of restored images. The structure of the AOT-GAN model is shown in Fig. 5.
The AOT-GAN model comprises a discriminator and a generator. The discriminator consists of a 5-layer stack of 2D convolutional layers progressively down-sampled through convolutional stir steps and padding using spectral normalization to stabilize parameter updates. The head and tail of the generator are three-layer encoder and decoder structures, respectively, and the feature extraction module in the middle layer consists of eight layers stacked with an AOT Block. The input consists of the training set images mined for information, which are complemented with a layer of masked images, which ultimately enables progressive pixel-level restoration. The encoder contains convolutional and pooling layers to extract high-level feature representations of the input image. The decoder contains an inverse convolutional layer and an up-sampling layer used to restore the feature representations extracted by the encoder to the original image size and complete the image reconstruction task. The AOT-GAN model is used to match the coded information inside and outside the missing region, and the pixel information is generated using copy-and-paste. The learning of the local features and global context information of the image in depth allows for a finer reconstruction of the missing regions, thereby improving the quality of the results.
Loss function
To ensure that the reconstructed images of the grotto murals have more realistic textures, more realistic content, and superior quality, the proposed GAN is trained using a joint loss function consisting of style, adversarial, and perceptual losses. The adversarial loss consists of the adversarial loss \({L}_{{\rm{adv}}}^{D}\) and \({L}_{{\rm{adv}}}^{G}\) for the discriminator and the generator, as shown in Eqs. (13–14), respectively:
where E denotes the expectation function; D and G denote the discriminative and generative networks, respectively; z denotes noisy data; x denotes the input features; m is an input binary mask, with 1 representing the missing region pixels, and 0 representing the known region pixels; Gaussian denotes the composite function of the Gaussian filter; ⊙ denotes the pixel-by-pixel multiplication process. In this process, only the prediction map of the masked region is optimized to improve the generator. The discriminator is optimized to counter and strengthen the generator, making the generated results more refined and realistic.
The Lrec loss function is used to guarantee the reconstruction precision at the pixel level.
Style loss is calculated using the L1 distance between the deep feature Gram matrix of the generated image and the real image, which helps improve the precision of the perceptual reconstruction process. The style loss, Lsty, is defined as
The role of perceptual loss is to minimize the L1 distance between the generated activation map and the real image during the reconstruction process. ϕ is the activation map obtained from the pre-trained network, and N denotes the number of elements in ϕ.
The perceptual loss, Lper, is defined as
The final overall loss function L is obtained as a combination of the individual losses. The weights λ are set artificially during the training process as λadv = 0.01, λ1 = 1, λper = 0.1, λsty = 250. A more realistic restoration result when the individual loss functions are weighted and co-optimized during model training.
Experiments and analysis of results
Overview of the study area
The Yungang Grottoes, located in Datong City, Shanxi Province, is one of the largest ancient grotto complexes in China, with high esthetic value and historical research significance. In recent times, murals of the Yungang Grottoes have been damaged to different degrees due to natural or man-made wear. Compared with traditional methods, repair methods based on digital imaging for mural damage detection not only reduce the difficulty of repair but also simplify the repair process and reduce the chances of damaging the grotto murals. They also have the advantages of high precision, rich content processing capability, and high flexibility, which makes them the preferred choice for mural damage detection prior to repair. In order to advance the damage detection and digital reconstruction of the murals in the grottoes, data collection during this study focused on Datong City (39° 54′–40° 44′ N, 112° 06–114° 33′ E), Shanxi Province, China. The location schematic is shown in Fig. 6. Through field visits to the Yungang Grottoes murals and photographing data at the Yungang Grottoes and Huayan Temple, it was possible to assess the damage to the murals more accurately and explore effective detection and restoration strategies.
Mural data preparation
The Yungang Grottoes’ mural images were captured using a high-definition Cannon EOS 6D digital single-lens reflex camera, with a resolution size of 5472 × 3648 pixels. Owing to the scarcity of the mural dataset, 276 images of grotto murals were collected in the experimental field. By filtering and organizing the 260 frescoes, a dataset of 1000 usable images was created through splicing, cropping, rotating, and segmenting operations. The selected 1000 images were divided into training, validation, and test sets at a ratio of 8:1:1.
As shown in Fig. 7, the LabelImg image annotation software was used to manually annotate the original mural dataset with the target bounding frames. Depending on the damage type, the frames were labeled as either Crack or Falloff, and the annotation information was saved in plain text format. The data were then organized in the necessary format to train the YOLO network.
The experiments were conducted under Windows 10 operating system; the CPU used was Intel Core i9-10900k at 3.7 GHz, and the GPU was NVIDIA GeForce RTX 4090 with 24,564MiB of video memory. The PyTorch 2.0.1 deep learning framework was used for this experiment; Python version 3.9, OpenCV2 library, and PyCharm were used as the development environment, and the GPU was accelerated using CUDA 11.8.
The optimal hyperparameter settings for grotto mural damage detection were obtained after several training and parameter tuning steps as follows: the initial learning rate was set to 0.1, the cosine annealing hyperparameter was set to 0.1, the weight decay coefficient was 0.0005, and the gradient descent momentum was 0.937. The number of iterations of the training process was set to 500, the batch size was set to 16, and the early stopping stochastic gradient descent strategy was used for training optimization. For the grotto mural digital reconstruction task, random mask images from an open-source set created by Liu et al.32 were used as the masking dataset, and the test set was used for the masking operation. For the training process, the batch size was set to 6, and the number of iterations was 30.
To comprehensively evaluate the performance of the YOLO Mural algorithm for grotto mural damage detection, special attention was paid to the computational efficiency, precision, and real-time detection performance of the model. The efficiency was evaluated through the number of parameters, floating-point operations (FLOPs), number of network layers, model storage size, and training time. In terms of precision, Precision (P), Recall (R), mean average precision (mAP), and reconciled mean (F1) were used as key evaluation criteria. The real-time detection performance of the algorithm was measured via the number of images or video frames per second (FPS), which can be processed to ensure that the response speed of the detection system meets the requirements of practical applications. In breakage reconstruction experiments, the results were analyzed quantitatively using the peak signal-to-noise ratio (PSNR), structural similarity (SSIM), mean square error (MSE), and mean absolute error (MAE).
In addition, mAP@0.5 was used to assess performance at the IoU threshold of 0.5, which refers to the overlap area of the predicted frame and the real frame being at least 50% of the total area of the two frames. For this operation, the average precision of the two damage classes was calculated, and then the average of the average accuracies was taken. For mAP@0.5:0.95, the IoU thresholds were divided into 10 equal parts in the interval from 0.5 to 0.95, and the average precision mean value was calculated for each threshold. The mean average precision evaluates the performance of the model under different IoU thresholds, which enables a more detailed assessment of the model’s ability to recognize prediction frames with different levels of overlap, thus providing richer information for model optimization.
Grotto mural damage detection experimental analysis
Comparative experiment
To validate the model performance of YOLO Mural, the model was compared to the YOLO series of models (YOLOv3, YOLOv5, YOLOv6, YOLOv7, YOLOv8, YOLOv9, and YOLOv10), as well as the RT-DETR models on the same test platform, using the same parameters and dataset. The test results are presented in Table 1.
As shown in Table 1, the YOLO Mural model has the fewest parameters and FLOPs and the smallest model size, which was 202.3MB less than that of the next-largest YOLOv3 algorithm. The YOLOv7 model was computationally intensive and its real-time was weak because it expands the high-efficiency layer aggregation network and the reparameterized network; this performance makes it difficult to deploy on mobile devices. In contrast, the number of parameters of YOLO Mural was only 7.12% that of YOLOv7, and the YOLO Mural algorithm required only 0.743 h to train, which was a reduction of 14.288 h compared to the RT-DETR model. YOLO Mural achieved a real-time detection speed of up to 289.32 fps. The lightweight YOLO Mural model lays the foundation for later deployment in hardware devices with limited computational resources.
Grotto murals exhibit a variety of damage patterns, ranging from tiny cracks to large areas of detachment. The types and degrees of damage may vary widely, which places extreme demands on the generalization ability of damage detection algorithms, leading to difficulties in breaking the 70% Precision mark. The proposed YOLO Mural algorithm achieved a precision of 72.7%, which was 56.68, 17.25, 9.32, 4.30, and 4.15 percentage points (pp) higher than that of YOLOv7, RT-DETR, YOLOv9, and YOLOv10, respectively. The YOLO Mural algorithm improved Recall by approximately 12.12 pp and mAP@0.5 by approximately 10.22 pp compared to YOLOv9, with a reconciled mean of 66%.
In addition, to better validate the performance of the algorithms, the customized YOLOv5s33, customized YOLOv7n34 GhostSECABI YOLOv5m16, and Ghost-C3SE YOLOv5m18 algorithm are reproduced, and comparative experiments are performed. The YOLO Mural algorithm is effectively lightweight compared to the algorithms in the literature33,34,16,18. Although literature33 only consumes 0.602 h, its model volume is still three times of YOLO Mural algorithm. Meanwhile, literature34 achieves a P of 67.3%. However, its real-time detection performance is only 114.7fps. Compared with the algorithm of literature16. YOLO Mural algorithm F1 value is improved by 13.7%. Meanwhile, the algorithm in literature18 for grotto mural detection has the lowest P of 56.7%. In summary, the YOLO Mural algorithm achieved an optimal balance of computational efficiency, detection speed, and precision in the task of grotto mural damage detection.
Ablation experiments
To verify the optimization effect of each module in terms of the grotto mural damage detection performance, a series of ablation experiments based on the YOLOv10 model was conducted. Three key modules are defined: module A referred to the StarBlock-SimAM technique for feature extraction enhancement; Module B referred to the integration of Efficient-RepGFPN to optimize the feature fusion process; and Module C referred to the introduction of the Inner-SIoU mechanism to improve the detection precision.
As shown in Table 2, compared with the baseline algorithm, the addition of the StarBlock-SimAM module in Model A improved the detection precision effectively, and its Precision and Recall were increased by 1.57 and 7.36 pp, respectively. The real-time detection speed of Model B, which adopted the Efficient-RepGFPN module for feature fusion, was 287.12fps, which proves that its feature fusion mechanism can better realize the information fusion of the high-level semantic features of the mural damage and the shallow delicate features. The precision of Model C with the replacement loss function of Inner-SIoU was 71.3%, which is a significant improvement at the expense of real-time detection. Models AB, AC, and BC were different combinations of the three modules. The precision of the proposed YOLO Mural algorithm was improved by 0.88, 1.53, and 1.11 pp compared to Models AB, AC, and BC, respectively.
Analysis of results
During the training process of the grotto mural damage detection model, the model calculates the loss function for the predicted results, which includes the bounding box, category, and confidence loss functions. The loss function is a measure of the model error between the predicted and real values, and provides feedback on the classification effect of the model, helping the neural network to adjust its weights adaptively and make the classification result more accurate. The bounding box, category, and confidence loss function of the damage detection process of the grotto murals are shown in Fig. 8a, b, and c, respectively.
The results indicate that the YOLOv10 and YOLO Mural algorithms exhibit similar convergence trends and final convergence values. However, in the early stages of model training, the YOLOv10 algorithm exhibited poor learning, generating individual fluctuation points that led to large fluctuations in the convergence of the loss function. By contrast, the YOLO Mural algorithm’s generalization of the detection effect was enhanced through the introduction of the loss function combining the Inner-SIoU, the internal scale intersection, and the ratio loss function. This made the model convergence process smoother and allowed the model to show stronger feature extraction and information fusion abilities, thus realizing an ideal damage detection effect.
mAP@0.5 is a comprehensive metric for evaluating model performance. Figure 9 shows the mean average precision curves of the YOLOv10 and YOLO Mural models. During the training process of the grotto mural damage detection model, the proposed YOLO Mural algorithm exhibited a faster precision improvement and a smaller fluctuation range than the original YOLOv10 algorithm. Moreover, the mAP@0.5 of the YOLO Mural and YOLOv10 algorithms were 64.73% and 59.28%, respectively, which constituted an improvement of 5.45 pp. However, the advantage bestowed by the lightweight nature of this algorithm is clear, as it can achieve a better balance between precision and speed as well as lower hardware requirements and consumption, thereby generating a smaller model size requiring shorter training times.
The P-R curves were obtained as the IoU threshold varied from 0 to 1. The R-P curves were formed by connecting the P and R values corresponding to each threshold point using the recall rate R as the horizontal coordinate and the precision rate P as the vertical coordinate. When precision and recall are combined through the P-R curve, the model’s reliability can be assessed in a quantitative manner. Larger areas under the curve, correspond to a better average model performance under different thresholds, which also indicates a higher reliability of the model.
The P-R curves are shown in Fig. 10, where it is evident that the area under the curve of the YOLO Mural algorithm is much larger than that of the baseline model. This result indicates that the improved model not only achieves significantly improved detection precision but also excels in maintaining high recall, thus significantly reducing false and missed detections.
In this study, the best model derived from the training process was used for the test trials, and 20 images from the test set were selected for a visual comparison of the real-time detection speed. A comparison of the real-time detection speeds of the YOLOv9, YOLOv10, and YOLO Mural algorithm models is shown in Fig. 11.
From Fig. 11, it can be seen that YOLOv9 required 7.5–9 ms to process each frame, with 9 images being processed in 8 ms each. The YOLOv10 algorithm required 4.5–6 ms to process each image, with 13 images being processed in 5 ms each. In contrast, the YOLO Mural processed each frame in 3–4 ms, with the detection time for 13 images remaining at 3 ms each. In contrast, YOLO Mural processed each frame in about 3 ms to 4 ms, and the detection time for 13 images was 3 ms. It can be seen that the proposed algorithm had a lower inference time and a relatively stable real-time detection speed. The YOLO Mural model improves detection precision while remaining lightweight, making it suitable for field deployment in support of cultural relic conservation tasks aided through digital means.
Visualization of test results
To visually compare the performance of the different algorithms in the detection and classification of grotto mural damage, the results of the YOLOv8, YOLOv9, YOLOv10, and YOLO Mural algorithms were compared, as shown in Fig. 12. It can be observed that the detection results of the proposed YOLO Mural algorithm are significantly better than those of the other algorithms.
As shown in Fig. 12a, the bounding box location of the YOLOv8, YOLOv9, and YOLOv10 models was not sufficiently precise when detecting a single grotto mural crack that was similar to the background, whereas the YOLO Mural algorithm could determine and place the bounding box more accurately, demonstrating better recognition and location performance. Meanwhile, Fig. 12b, c shows that the YOLO Mural demonstrated a higher confidence level than the other algorithms.
This indicates that it is possible to distinguish more subtle crack damage from similar backgrounds more effectively through the introduction of the attention mechanism. Figure 12d, e, are examples where the YOLOv8, YOLOv9, and YOLOv10 models exhibited unsatisfactory detection effects, with simultaneous false negatives and generally low confidence in the detection results. After the introduction of the Efficient-RepGFPN feature fusion network, the information fusion ability was improved, solving the problem of subtle crack detection effectively and accurately recognizing the damaged regions of the mural with a higher confidence level.
The misdetections of the YOLOv8 and YOLOv10 algorithms are compared in Fig. 12f. The algorithm proposed in this work was very sensitive to crack damage and could accurately distinguish between cracks and grotto murals curves in the grotto murals examined. It could also detect small areas of detachment accurately, which demonstrates a superior detection effect.
In addition, the heat map visualization results of the algorithmic model were developed by the Grad-CAM method. The heat map visualization results are shown in Fig. 13. A heat map visualization was used to gain insight into the impact on classification judgments and target localization in the images. The recognition results in Fig. 13 show that the network improvements are effective in improving the recognition performance of the models. Specifically, each model focuses on different regions of focus in detection with different focusing capabilities. The original YOLOv5 model fails to focus on the broken region in the center of the image. the YOLOv5 model can only focus on a small number of regions, and other algorithmic models focusing on the breakage are prone to miss the cracks more. The YOLO Mural model proposed is able to focus on more key features in the broken region.
In general, when it comes to damage detection in grotto murals, the practicality and potential of digital cultural relic analysis using deep learning algorithms are remarkable. The experimental results of the novel YOLO Mural algorithm, which is based on YOLOv10, show that its detection effect was better than that of the original algorithm and that it could detect damages in grotto frescoes through computer vision.
In general, when it comes to damage detection in grotto murals, the practicality and potential of digital cultural relic analysis using deep learning algorithms is remarkable. The experimental results of the novel YOLO Mural algorithm, which is based on YOLOv10, show that its detection effect was better than that of the original algorithm and that it could detect damages in grotto frescoes through computer vision.
Grotto mural restoration experimental analysis
Comparison of repair results
In order to test the method in a more practical way, actual damaged murals are used as objects. In this study, Patch-GAN35, StyleGAN236, and DIGAN37 algorithms are chosen to verify the effectiveness of the proposed method. For the 26 images restored by different algorithms, and the mean values of the corresponding evaluation metrics are calculated. The PSNR, SSIMMSE, and MAE metrics are chosen to evaluate the resultant images, and the experimental results are shown in Table 3.
It can be seen that the PSNR of StyleGAN2 algorithm is 32.85 dB, which indicates that the quality of the restored image is good. However, it is still inferior to the AOT-GAN algorithm.Patch-GAN and StyleGAN2 algorithms have the same SSIM value of 0.95, which indicates that the structure of the image is well maintained and the similarity is high. DIGAN algorithm has the worst restoration effect.AOT-GAN algorithm has the best performance in the four indexes, especially the PSNR and SSIM are the highest, and the MSE and MAE are the the smallest, indicating that the model is able to retain the quality and details of the image well in the restoration of cave murals.
Visualization of digital reconstruction results
The results of the digitally reconstructions of the broken grotto murals are shown in Fig. 14. As shown in Fig. 14, Fig. 14a is the original image of the real broken mural, Fig. 14b is the corresponding mask image of the broken region, Fig. 14c is the corresponding broken region detected by the YOLO Mural target detection algorithm proposed, and Fig. 14d is the result of the restoration of the AOT-GAN algorithm.
From the restoration results of the first mural, it can be seen that the AOT-GAN algorithm corresponds to the three rectangular boxes in the restoration results of texture consistency, line continuity, and the overall color coordination and naturalness, the visual feeling is better. For the second mural, there is only one broken rectangular box, cracks in the case of better repair, but there are still small areas of broken unfinished and the existence of residual traces. As seen in the third mural, the AOT-GAN algorithm can fit the contours of the hand and the vase better, and the repair is more complete. Color splicing is more complex in the fourth mural of small areas of damage, there is no boundary information has a little missing and fuzzy and other problems, can be seen in the AOT-GAN algorithm in the structure of the continuity and color consistency have been improved. For the repair of large damaged areas in the fifth and sixth murals, the AOT-GAN algorithm repair results are more complete. Even in the face of large damage areas, realistic texture content and color were created, and no blurriness artifacts were observed. It can be observed from the comparison that the digital reconstruction of the damaged mural images was effective, both in color and texture repairs, and the results were realistic (Fig. 14).
a is the original image of the real broken mural, b is the corresponding mask image of the broken region, c is the corresponding broken region detected by the YOLO Mural target detection algorithm proposed, and d is the result of the restoration of the AOT-GAN algorithm. The AOT-GAN algorithm is trained under the homemade Yungang Grottoes mural dataset used in this paper, and the experimental results are obtained by restoration using the test set within the dataset plus a random mask32.
On the other hand, the PSNR, SSIM, MSE, and MAE of the AOT-GAN restoration model were 34.842, 0.9832, 30.459, and 0.0027, respectively, and the performance of the AOT-GAN restoration model in the restoration of grotto murals was excellent in terms of both the subjective evaluation and objective criteria.
Conclusion
In this paper, a dataset with photographic images of the Yungang Grotto murals was created, which included different viewpoints and lighting conditions. The dataset aims to provide rich resources for the digital protection of cultural heritage, academic research, and technological developments.
In addition, an algorithm was proposed to detect damages in grotto murals. The algorithm, which is based on YOLOv10, combines an attention mechanism, which is used to create a new lightweight residual module, with the introduction of a new feature fusion network. These modules remove redundant feature information effectively, and increase the accuracy and depth of the feature extraction process, which results in an improved precision and detection speed of the model. To support the training process accordingly, the loss function was optimized to improve the location performance of the damage detection effectively.
Following damage detection, a generative adversarial network was employed to digitally reconstruct the broken areas of the grotto murals. The network could effectively infer realistic content suitable for filling the damaged areas of the grotto murals and compensated effectively for the color and quality defects of the images, thus providing support for the applicability of natural image reconstruction models in grotto mural restoration applications. The network structure is simple and does not require substantial computational resources.
Future research will prioritize the expansion of high-quality mural damage datasets, with a particular focus on diversifying annotations for rare damage types to enhance the learning capabilities of models for both damage detection and image restoration. The combination of deep learning and reinforcement learning will also be investigated to enable adaptive learning capabilities, supporting further optimization of both detection and restoration accuracy alongside real-time performance. These advancements are intended to drive the development of efficient digital technologies for cultural heritage conservation, combining automated damage assessment with accurate image reconstruction. Continuous optimization in these areas is expected to significantly enhance the practical application and scientific impact of the proposed approach, providing robust and reliable technical solutions for preserving and restoring cultural heritage.
Data availability
No datasets were generated or analyzed during the current study.
References
Zhao, H. R., Yu, Y., Zhao, N. & Wang, Q. Detection of damaged areas in ancient murals based on multi-scale dual channel attention U-Net. 2024 4th International Conference on Neural Networks, Information and Communication Engineering (NNICE) 1069–1074 (Guangzhou, China, IEEE 2024).
Tint, K. K. W. & Tin M. M. Digital restoration of ancient murals: assessing the efficacy of coherent transport inpainting with damage ratio analysis. IEEE Conference on Computer Applications (ICCA) 1–8. (IEEE, Yangon, Myanmar, 2024).
Du, P. A comprehensive automatic labeling and repair strategy for cracks and peeling conditions of literary murals in ancient buildings. J. Intell. Fuzzy Syst. 46, 3557–3568 (2024).
Mishra, M. & Lourenço, P. B. Artificial intelligence-assisted visual inspection for cultural heritage: State-of-the-art review. J. Cult. Herit. 66, 536–550 (2024).
Qiao, K. Z., Hou, M. L., Lyu, S. Q. & Li, L. H. Extraction and restoration of scratched murals based on hyperspectral imaging—a case study of murals in the East Wall of the sixth grotto of Yungang Grottoes, Datong, China. Herit. Sci. 12, 123 (2024).
Yu, K. et al. Automatic labeling framework for paint loss disease of ancient murals based on hyperspectral image classification and segmentation. Herit. Sci. 12, 192 (2024).
Tang, H. D. et al. Application of object detection algorithm for efficient damages identification of the conservation of heritage buildings. Archaeol. Prospect. 31, 233–247 (2024).
Zhang, W. Z., Sun, Z. Z., Mei, J. & Xu, B. S. Intelligent recognition and parameter acquisition of blastholes in rock tunnel based on improved Faster R-CNN. Tunn. Undergr. Space Technol. 149, 105790 (2024).
Ren, H., Sun, K., Zhao, F. H. & Zhu, X. Dunhuang murals image restoration method based on generative adversarial network. Herit. Sci. 12, 39 (2024).
Li, X. X. et al. An efficient transformer network for detecting multi-scale chicken in complex free-range farming environments via improved RT-DETR. Comput. Electron. Agri. 224, 109160 (2024).
Wu, L. G., Zhang, L., Chen, L., Shi, J. H. & Wan, J. F. A lightweight and multisource information fusion method for real-time monitoring of lump coal on mining conveyor belts. Int. J. Intell. Syst. 2023, 5327122 (2023).
Wu, L. G., Chen, L., Zhou, Q., Shi, J. H. & Ma, Y. B. A maturity detection method for Hemerocallis Citrina Baroni based on lightweight and efficient layer aggregation network. Trans. Chin. Soc. Agric. Mach. 55, 268–277 (2024).
Wu, L. G., Chen, L., Liu, Z. P., Ma, Y. B. & Wu, Y. Q. YOLOv8-ABW based method for detecting Hemerocallis citrina Baroni maturity. Trans. Chin. Soc. Agric. Eng. 40, 262–272 (2024).
Wu, L. G., Chen, L., Zhang, L. & Shi, J. H. A lump coal detection method fusion of lightweight and attention mechanism. IEEE J. Emerg. Sel. Top. Ind. Electron. 5, 763–771 (2024).
Wu, L. G., Chen, L., Shi, J. H. & Wan, J. F. SNW YOLOv8: improving the YOLOv8 network for real-time monitoring of lump coal. Meas. Sci. Technol. 35, 105406 (2024).
Wu, L. G. & Zhang, L. Damage detection method for grotto murals based on lightweight neural network. Inf. Control 53, 108–119 (2024).
Gao, C. et al. Applying optimized YOLOv8 for heritage conservation: enhanced object detection in Jiangnan traditional private gardens. Herit. Sci. 12, 31 (2024).
Wu, L. G., Zhang, L., Zhang, Y. & Wan, J. F. Damage detection of grotto murals based on lightweight neural network. Comput. Electr. Eng. 102, 108237 (2022).
Marín-Marín, S. C., López-Martínez, T. & Medina-Flórez, V. J. Aadhesion systems in new supports for mural paintings: reversibility tests. Stud. Conserv. 5, 1–16 (2024).
Priego, E., Herráez, J., Denia, J. L. & Porres, M. J. Pictorical reintegration of mural paintings to the irregular surface of the vault of the church of Santos Juanes in Valencia (Spain) through 3D digital techniques. Digit. Appl. Archaeol. Cult. Heritage 34, e00361 (2024).
Shcheviova, U., Karol, W. & Aleksander, S. Preserving authentic decoration in the entrance spaces of residential buildings in eastern galicia from the late 19th to the first third of the 20th century: restoration experience. Int. J. Conserv. Sci. 15, 993–1008 (2024).
Merizzi, F. et al. Deep image prior inpainting of ancient frescoes in the Mediterranean Alpine arc. Herit. Sci. 12, 41 (2024).
Ugail, H., Stork, D. G., Edwards, H., Seward, S. C. & Brooke, C. Deep transfer learning for visual analysis and attribution of paintings by Raphael. Herit. Sci. 11, 268 (2023).
Chen, Y., Tao, M. F. & Zhao, M. X. Generative adversarial network for mural inpainting based on multi-level feature fusion and hypergraph convolution. Adv. Eng. Sci. 56, 208–218 (2024).
Aswathy, A. & Maheswari, P. U. Generative innovations for paleography: enhancing character image synthesis through unconditional single image models. Herit. Sci. 12, 258 (2024).
Ma X., Dai X. Y., Bai Y., Wang Y. Z. & Fu Y. Rewrite the stars. In: Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. 5694–5703 (IEEE, 2024).
Han, G. G., Huang, S. L., Zhao, F. & Tang, J. L. SIAM: a parameter-free, spatial intersection attention module. Pattern Recognit. 153, 110509 (2024).
Zhou, Y. A YOLO-NL object detector for real-time detection. Expert Syst. Appl. 238, 122256 (2024).
Zhang, H., Cong, X. & Zhang, S. J. Inner-IoU: more effective intersection over union loss with auxiliary bounding box. (2023). https://arxiv.org/abs/2311.02877
Wang, A. et al. Yolov10: Real-time end-to-end object detection. (2024). https://arxiv.org/abs/2405.14458
Zeng, Y. H., Fu, J. L., Chao, H. Y. & Guo, B. N. Aggregated contextual transformations for high-resolution image inpainting. IEEE Trans. Vis. Comput. Graph. 29, 3266–3280 (2022).
Liu, G. L. et al. Image inpainting for irregular holes using partial convolutions. Proceedings of the European Conference on Computer Vision (ECCV), Vol. 11215, 85–100 (Springer, Cham, 2018).
Karimi, N., Mayank, M. & Paulo, B. L. Deep learning-based automated tile defect detection system for Portuguese cultural heritage buildings. J. Cult. Herit. 68, 86–98 (2024).
Mishra, M. & Barman, T. & Ramana, G. V. Artificial intelligence-based visual inspection system for structural health monitoring of cultural heritage. J. Civ. Struct. Health Monit. 14, 103–120 (2024).
Chen, G., Zhang, G. P., Yang, Z. G. & Liu, W. Y. Multi-scale patch-GAN with edge detection for image inpainting. Appl. Intell. 53, 3917–3932 (2024).
Viazovetskyi, Y., Ivashkin, V. & Kashin, E. StyleGAN2 distillation for feed-forward image manipulation. Computer Vision ECCV 2020. Lecture Notes in Computer Science. Vol 12367 (Springer, Cham, 2020).
Yan, L. Q. et al. DIGAN: distillation model for generating 3D-aware Terracotta Warrior faces. Herit. Sci. 12, 317 (2024).
Acknowledgements
This work was supported by the Shanxi Province Basic Research Program (202303021211330), the Datong Municipal Science and Technology Program (2023015), and the Basic Research Fund of Datong University, Shanxi (2022K1). The Shanxi Province Basic Research Program (202303021211330), Datong Municipal Science and Technology Program (2023015), Basic Research Fund of Datong University, Shanxi (2022K1), and Guangzhou Science and Technology Plan Project (2024B03J1297).
Author information
Authors and Affiliations
Contributions
W.L.G. designed the idea and led the writing of the article, C.L. and W.J.F. conducted the experiment and collected the data. C.L. conducted the analysis and supervised the whole process. All authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Chen, L., Wu, L. & Wan, J. Damage detection and digital reconstruction method for grotto murals based on YOLOv10. npj Herit. Sci. 13, 91 (2025). https://doi.org/10.1038/s40494-025-01607-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s40494-025-01607-z