Multiscale hierarchy denoising method for heritage building point cloud model noise removal

Abstract

In recent years, interest in the three-dimensional (3D) data documentation of heritage buildings has been growing. The collection of detailed and accurate 3D point-cloud information by acquiring heritage-building data has facilitated various applications. These applications encompass historical architectural information retrieval, preservation and monitoring, augmented reality, virtual reality, and the generation of heritage building information models. Point clouds originate from 3D scanners, human–computer interactions, and other devices exposed to unnecessary environments. In this context, point clouds are inevitably affected by noise and outliers. Factors contributing to noise include the limitations of sensors, device defects, and the illumination or reflection characteristics of the studied objects. Thus, addressing noise and outliers presents a challenge when storing point cloud data. Denoising is a critical step in data processing for point clouds when applied to heritage architecture. The accuracy of the point cloud model in heritage architecture is highly dependent on noise and outliers. This study proposes a multiscale hierarchy denoising method, the process of which is as follows. First, we divided the point cloud model of heritage architecture according to the architectural structure. The density-based spatial clustering of applications with noise algorithm was then used to perform large-scale point cloud denoising. For small-scale noise, denoising is achieved on a macroscopic basis by systematically removing noise and outliers from the heritage architectural point cloud model using statistical and bilateral filtering techniques. This process improves the quality and accuracy of point cloud data related to heritage buildings.

Introduction

Architectural heritage is a vital conduit for regional cultural identity, representing historical material legacies and cultural assets vital to a region’s continued growth¹. Natural changes and the cultural evolution of society have caused significant harm to many historic architectural buildings, and their loss is a real possibility. In particular, the devastation caused by major disasters has highlighted the importance of risk prevention and heritage protection. The emergence of three-dimensional (3D) laser scanners has garnered considerable attention and has been widely applied in various domains². The rapid evolution of 3D laser-scanning technology has facilitated the acquisition of precise point clouds that represent ground targets, making point-cloud processing techniques a focal point in the realm of visual processing. The application of laser scanning in heritage architecture has attracted attention because of its capacity to generate high-precision data³. In most scenarios, the entire required site can be comprehensively scanned. Researchers can obtain comprehensive information about large heritage buildings through point cloud data, thereby offering promising technological potential for large-scale applications such as the conservation of cultural heritage buildings⁴ (Fig. 1).

Fig. 1

3D laser-scanning process for heritage buildings.

In the processing of heritage architecture data, denoising is a crucial step for acquiring high-precision point cloud models. Point clouds, composed of numerous discrete points, form a 3D dataset that captures the surface shape and structural information of buildings using techniques such as laser scanning⁵. However, owing to limitations in device precision, the influence of lighting and material reflection characteristics, and environmental conditions during scanning, the obtained data often introduces noise points and outliers, significantly compromising the accuracy and quality of point cloud models and, in some cases, altering the topology of the model⁶. Point cloud data frequently incorporate noise, representing inaccurate or unnecessary points that may impact research, analysis, and applications related to heritage architecture.

An effective method for noise elimination is filtering, which is an indispensable pre-processing stage. This stage is necessary to obtain precise point clouds suitable for further processing, such as modelling and reconstruction⁷. Various methods exist for point cloud denoising, including statistical and segmentation-based denoising. However, for structurally complex large-scale heritage buildings, most denoising methods can only reduce the noise and fail to eliminate redundant components. A singular denoising approach often lacks precision in removing noise points and outliers.

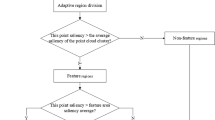
Building on prior research, this study introduces a hierarchy denoising method tailored to point cloud models of structurally complex individual heritage buildings. First, based on the hierarchical structure of heritage architecture point clouds, segmentation is performed primarily by employing cloth simulation filtering (CSF), slope, and pass-through filtering. This segmentation divides the point cloud model into ground, walls, corridors, interiors, and roofs, with further subdivisions into detailed architectural decorative component point cloud models based on fundamental building structures. Second, the DBSCAN algorithm was employed to analyse the clustering of the heritage architectural structural point cloud models. Finally, statistical filtering was used to remove larger-scale outliers, and bilateral filtering was applied to eliminate small-scale noise in the heritage architectural decorative structures. In this study, the hierarchy denoising method, which addresses complex heritage architecture point cloud models, comprehensively removes noise and outliers based on a structural hierarchy. It effectively eliminates noise points in both the platform areas and complex structural regions.

This study used Great Achievement Palace in the old city of Yuci, Shanxi, China, as an example to illustrate the denoising of point cloud data with the aim of obtaining a high-precision quality point cloud model. The ‘Temple of Literature’, a specific label for Chinese civilisation, is a shrine building commemorating and worshipping Confucius, a great Chinese thinker, statesman, and educator. The Temple of Literature in Yuci Old Town, on the north side of Longwangmiao Street in Yuci City—with a floor area of 6000 square metres—is the most ancient existing building in Yuci, which was built by the county magistrate, Gong Fu, in the second year of Xianping of the Northern Song Dynasty (999 AD), and is a key cultural relics protection unit in Yuci.

Great Achievement Palace, the central building of the Yuci Old City Confucian Temple, is a place of worship dedicated to Confucius. It was renamed the Great Achievement Palace in the third year of the Chongning era of the Song Dynasty (1104 AD)⁸. The building covers an area of 877 square metres, with a width of nine bays, depth of five bays, and height of over 18 m. It is a Song-style building with a single-layered, double-eaved, Xieshan-style roof. Surrounded by 28 coiled dragon stone pillars, this structure exudes a majestic and solemn demeanour. The Great Achievement Palace of Wenmiao (Confucian Temple) in Yuci Old Town holds a significant position in the history of world architecture. Its architectural style and layout reflect the characteristics of Song Dynasty architectural art, with exquisite wood carvings and stone sculptures serving as important tangible materials for studying ancient buildings and craftsmanship.

The most recent major renovation of Great Achievement Palace occurred in 2004; since then, heritage departments have organised multiple maintenance efforts for the building. Processing denoised point cloud data for heritage buildings is important for the study and conservation of Great Achievement Palace. Historical restoration has relied on two-dimensional drawings, photographic documentation, and historical records. The 3D point cloud model, obtained through laser scanning or other measurement technologies, provides a 3D plan for heritage building restoration. Point cloud denoising is a crucial step in the conservation and restoration of heritage buildings. Raw 3D data may contain noise, such as erroneous points or non-building elements, and the denoising process significantly improves data accuracy, resulting in a more realistic and precise final 3D model⁹. Denoised point cloud data are more suitable for structural analysis, deformation monitoring, and stress analysis, offering architects and engineers more accurate references for designing restoration plans that better reflect the actual conditions of Great Achievement Palace. Additionally, high-quality point cloud data help create detailed digital archives, documenting the building’s current state and historical changes, which are crucial for the conservation, restoration, and future research of Great Achievement Palace.

Literature review and theoretical discussion

Point cloud denoising can aid in eliminating noise and unnecessary details, thereby improving the accuracy of heritage-building point cloud models. The current state of heritage buildings can be recorded more accurately using high-precision point cloud models. This is crucial for the long-term preservation of cultural heritage because the recording provides detailed information that is helpful in making restoration and conservation plans. Without proper processing, point cloud data may cause the algorithm to fail and produce adverse results in the estimation of geometric primitives and, in turn, affect the semantic interpretation of the scene and 3D modelling. For instance, the extraction of geometric primitives, which is vital to segmentation algorithms or surface fitting, is affected by noise in the features¹⁰. To illustrate this, Cui et al. described how line-based 3D reconstruction methods are affected by excessive false details owing to noise responses, thereby affecting the quality of the constructed model¹¹.

Segmentation denoising filtering algorithm

Filtering is a fundamental prerequisite before the data can be used in various aspects of point cloud processing¹². Point cloud filtering methods are frequently used to remove noise and outliers. The filters used for segmentation, such as CSF, slope, and pass-through filtering, employ these methods to eliminate noise points and segment outliers.

CSF is an algorithm based on the assumption of a physical concept. Its core idea involves simulating a piece of ‘cloth’ made of virtual particles. Because of gravity and internal forces, it naturally falls onto the ground surface. At this point, the ‘cloth’ approximates the actual surface of the earth, with ground points and feature points separated by a height threshold. This method focuses on extracting ground points¹³.

The algorithm for slope filtering was initially introduced by Vosselman¹⁴ and was initially used for terrain elevation in digital elevation models (DEMs). Its concept is based on distinguishing ground points from non-ground points based on differences in slope. Wan et al. proposed a multiscale adaptive point cloud slope filtering algorithm that combined k-means clustering and normal distribution to adaptively determine thresholds and address adaptive issues in slope filtering. Slope-based ground-filtering algorithms calculate the height difference and slope between points within a certain range by setting thresholds based on the inconsistent slopes between ground points and objects¹⁵. It is suitable for flat areas but is less effective in areas with dramatic terrain changes. Furthermore, objects close to the ground are often incorrectly classified as ground points¹³.

Pass-through filtering is effective for point clouds with significant spatial distribution differences between the valid and elimination points. The pass-through filtering algorithm works by filtering out points not within a given threshold range in a specified dimensional direction and filtering out points whose values in the specified dimension are not within the domain¹⁰.

Battini et al. proposed a methodology for classifying and segmenting heritage-building vaults. Building on fundamental geometric rules and shape grammar, they employed software and additional tools to isolate and partition architectural vaults with the primary goal of achieving comprehensive classification and capturing intricate geometric details¹⁶. Zaragoza et al. ensured the integrity and accuracy of point cloud data through noise removal, outlier detection, and registration. They then applied feature extraction and segmentation algorithms such as random sample consensus (RANSAC) and region growing to identify the key architectural elements and decorative details¹⁷. Caciora et al. utilised k-means clustering, RANSAC, and facets methodology to classify and segment regional structures. In addition, the use of combined indices encompassing multiple geometric features of a scene contributes to obtaining detailed results and enhances the accuracy of the assessment¹⁸. Wang et al. proposed a hierarchical denoising strategy based on spherical space finite measurable segmentation. However, this method may result in the removal of certain intricate architectural decorative elements during the segmentation process, particularly in complex heritage buildings¹⁹. Ismail et al. proposed a subgrouping based on surface and unstructured points. All defective noise points were grouped into an unstructured set, and elements such as building facades and streets were categorised accordingly. Unstructured groups can be retained as points for visualisation or used for further classification to identify smaller objects, trees, and noise²⁰.

Large-scale noise denoising methods

Researchers have proposed various methods for large-scale noise reduction in point clouds of heritage buildings. Di Filippo et al. used Poppaei Villa at the Oplontis site in Pompeii as a case study to demonstrate a filtering method that removed and reduced noise while preserving the original surface details of an object²¹. However, the descriptions of these technical aspects are relatively sparse.

Cluster analysis is an unsupervised machine-learning technique. Two common types of clustering-based filtering algorithms are known: distance-based and density-based spatial clustering algorithms²². Because of the susceptibility of distance-based clustering algorithm to noise, the density-based spatial clustering algorithm is often used to denoise 3D point cloud data. Density-based spatial clustering of applications with noise (DBSCAN) is a widely used clustering technique that is highly effective in removing noisy points. DBSCAN is a popular density-based clustering algorithm, and it introduces a model using a simple minimum density level estimation, based on a threshold of a neighbouring quantity minPts within radius ε. Objects (including the query point) within this radius with more than minPts of neighbouring objects are considered core points. All neighbours within the ε radius of a core point are deemed part of the same cluster (directly density-reachable). If any of these neighbours become core points, their neighbourhoods are passed on inclusively (density-reachable). Non-core points in the set are called border points, and all points in the same set have a density connectivity. Points that are not density-reachable from any core point are considered noise and do not belong to a cluster. Ni et al. proposed a point cloud filtering algorithm that combines clustering and iterative graph cutting, categorising, and processing point cloud data acquired by LiDAR.

Small-scale noise denoising methods

To date, numerous point cloud filtering algorithms have been developed. Carrilho et al. introduced a statistical outlier removal (SOR) filter as an outlier removal strategy. This filter distinguishes between outliers and noise by calculating the average distance between each point and its nearest K neighbours²³. Wolff et al. validated their denoising and outlier removal algorithms using several multi-view datasets²⁴. Čvorović et al. applied statistical filtering to sculptures, finding that the model quality has improved through index analysis after data processing²⁵.

The SOR filter identifies point cloud outliers located in areas where the data density is below the threshold. Therefore, the algorithm calculates the average distance between points in a 3D point cloud²⁵. In this step, the algorithm uses the k-nearest neighbours to compute the average distance. The overall mean and standard deviation were calculated. Finally, the threshold is calculated as n × standard deviation, where n is a user-defined input value²⁶. The average distance between each point and all its neighbours was determined by computing the distribution of the distances between the query points and neighbouring points in the input data. Points with average distances exceeding the standard range were defined as outliers and removed from the data²⁷.

Si et al. proposed a bilateral filter as a fast, lightweight, and effective denoising tool. Zhang et al. optimised the denoising process using bilateral filtering. They used a normal-based point cloud bilateral filter as a platform and introduced a new normal preservation concept that significantly improved the overall performance of the denoising process¹. Jin et al. employed a combination of statistical and bilateral filtering for point cloud processing²⁷. They used statistical filtering to remove a large amount of noise from laser point clouds, and under bilateral filtering, the laser point clouds were smoothened and denoised while preserving their characteristics of the point clouds. A large amount of point cloud voxel grid filtering maintains point cloud volume conciseness while accelerating the point cloud filtering speed and improving the efficiency of laser point cloud data processing. Bilateral filtering smoothed out noise points. Ren et al. used 3D point cloud data bilateral filtering to remove small-scale noise points from rocky surface mutation areas¹³. Zheng et al. proposed methods to remove large-scale noise using an improved bilateral filtering algorithm and a weighted average filtering algorithm based on grey relational analysis for filtering feature-rich and flat areas, respectively²⁸. Yin et al. applied a bilateral filtering algorithm to denoise point cloud data collected from the ancient Yiyuan architecture. The maximum error in the two-dimensional model generated from point cloud data was only 0.007 m, and the error in the 3D model was controlled within 9 mm²⁹. Lin et al. addressed the denoising problem of 3D point-cloud colour data by proposing two specialised denoising algorithms based on the noise characteristics in different spatial domains. In the denoising process, the RGB colour space is first converted into the YUV colour space for further denoising operations. Surface smoothing is achieved using a median or bilateral filter³⁰. Wang et al. proposed a smoothing and denoising process for ancient tower point cloud models. This method achieves denoising by calculating the distance from each point to a local fitting surface and excluding the outlier points³¹.

Denoising methods in complicated situations

Li et al. proposed a denoising method that can be applied in complicated situations. Initially, this means classifying object extraction and clustering roughly, and separating the entire data into target points. Subsequently, based on the different point distributions for each category, corresponding denoising strategies were designed to eliminate outliers. By applying a two-stage method, they obtained a point cloud with fewer outliers³². Ren et al. developed an innovative overall filtering algorithm that combines statistical filtering in flat areas and bilateral filtering in mutated areas. It removes large- and small-scale noise close to the rock surface, thus completing a multiscale noise removal process for point clouds¹³. Lin et al. obtained low-redundancy, high-fidelity point cloud data from the Great Wild Goose Pagoda using multiple filtering and point cloud segmentation techniques³³.

The research of the aforementioned authors also provided insights into denoising point cloud models of heritage buildings. In this context, an attempt was made to remove noise and outliers from complex heritage building point cloud models using structural hierarchical denoising.

The requirements for denoising point clouds of heritage buildings

The requirements for denoising point clouds of heritage buildings primarily focus on preserving the structural features, intricate details, and historical value of the buildings while eliminating erroneous points or stray data caused by noise, interference, or improper scanning during data acquisition.

These requirements are explicitly outlined in several technical standards and specifications. According to the Technical Specification of Three-Dimensional Information Acquisition of Heritage Buildings (DB11/T 1796-2020), the denoising requirements are outlined as follows: In Section 8.3.1.8, point 3, it is specified that the denoising process must not affect the extraction and recognition of feature points. In Section 8.3.2.4, it is required to remove isolated noise points and filter noise points on the surface of the point cloud. Additionally, section 8.3.2.4 specifies the need to remove free-floating noise points and filter out noise on the surface of the point cloud.

In the Technical Specifications for Terrestrial Three-Dimensional Laser Scanning (CH/Z 3017-2015), the denoising of point clouds for heritage buildings should comply with the following regulations: when abnormal or isolated points detached from the scanned target object are present in the point cloud data, filtering or human-machine interaction should be used for denoising. Similarly, in the Regulations for 3D Laser Scanning and Digital Acquisition of Cave Temple Cultural Relics (DB 14/T 1926-2019), it is stipulated that when abnormal or isolated points detached from the scanned target object are present in the point cloud data, denoising should be performed using filtering methods or manual intervention, depending on the number of points.

From these technical standards, it is evident that the quality requirements for denoising point clouds of heritage buildings involve not only the removal of free-floating noise, abnormal points, and surface noise but also mandate the preservation of the building’s structural features and intricate details.

In this study, Gaussian distribution graphs and visualisations of the model were employed to illustrate the experimental variations in denoising and the resulting denoising quality with the aim of comparing the advantages and disadvantages of different denoising methods.

Methods

This study investigates the application of various methods (e.g. slope filtering, pass-through filtering, DBSCAN clustering, statistical outlier removal filtering, and bilateral filtering) for denoising point clouds of heritage buildings and proposes a different denoising approach based on the structure. The feasibility of these methods was also assessed.

Given the complex structure of heritage building point cloud models, eliminating noise and outliers is necessary by using different denoising approaches based on the structure. In this study, point cloud denoising and outlier removal methods were improved. Initially, the point clouds of the heritage buildings were filtered through the structural layers. Using CSF, slope filtering, and pass-through filtering, the point cloud model of the heritage building was segmented into different regions. Subsequently, large-scale point cloud model denoising was performed. Although the DBSCAN algorithm is based on density, it analyses whether sparse point clouds are noisy points or outliers. Small-scale point cloud model denoising was then performed by removing low-density area noise points using the SOR method. Finally, the surface point clouds of the buildings were smoothed through bilateral and smoothing filtering, preserving their structural contours.

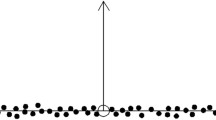
Point cloud noise can be classified into large- and small-scale noise²⁸. Large-scale noise is significantly distant from the normal feature points, whereas small-scale noise is intermixed with the normal feature points. In this study, large-scale noise refers to the sparse partitions that can be observed as substantial anomalies. Small-scale noise refers to indistinct points that are easily confused with point cloud models of building components and are challenging to denoise through segmentation (Fig. 2).

Fig. 2

Heritage building point cloud denoise framework.

Results and discussion

Heritage building point cloud component feature hierarchical segmentation

The feature segmentation and denoising of heritage architectural components in point cloud data processing are typically combined and both work collaboratively to enhance the quality of the final results. Therefore, in this study, a structural hierarchical approach is proposed, starting with segmentation based on the structure of the heritage architectural point cloud model. Pass-through and slope filtering were applied to segment the heritage architectural point cloud model. Pass-through filtering categorises heritage architectural point clouds based on architectural structures, such as walls, floors, roofs, and interiors. Large-scale outliers were removed during this process.

Owing to the significant proportion of ground points in heritage building point cloud models and considering that real-world ground surfaces are often uneven, it is important to account for changes in ground slope and noise during ground segmentation. The principle of slope filtering involves determining whether a point belongs to the ground using filtering based on the slope. Large height differences between two adjacent points are less likely to be caused by steep topographical terrain. Instead, it is more likely that a higher point is not a ground point. For certain height differences, the probability that the higher point is a ground point decreases if the distance between two points decreases.

The CSF ground point-filtering algorithm employs principles derived from cloth simulations to emulate the characteristics of ground point clouds. This algorithm effectively eliminated ground points by juxtaposing actual point cloud data with a simulated cloth model. As illustrated in Fig. 3, the utilisation of the CSF algorithm within the CloudCompare software facilitates the segregation of ground point clouds.

Fig. 3

Ground segmentation using the cloth simulation filter (CSF) on the floor of the Great Achievement Palace.

The principle of pass-through filtering is relatively straightforward, making it a fundamental noise-reduction technique. Pass-through filtering operates by setting a channel based on a point cloud spatial coordinate system. It then eliminates points outside the channel range, thereby preserving the point clouds within the range. In the context of official Chinese architecture, architectural standards such as size, height, and decorative components vary across different periods but adhere to specific dimensions. Consequently, using pass-through filtering to divide the point-cloud model according to the architectural form and size results in a more accurate segmentation outcome (Figs. 4 and 5).

Fig. 4

Hierarchical structure by pass-through filtering.

Fig. 5

Segmentation based on architectural structure.

Slope filtering facilitates the partitioning and filtering of points on inclined surfaces, based on varying slope values. In the case of point cloud models of heritage buildings, intricate decorative structures, such as roofs with different slopes, can be regionally segmented using slope filtering. For items such as furnishings and door and window components, pass-through filtering can be applied for secondary segmentation (Fig. 6).

Fig. 6

Segmentation of architectural decorative components.

Heritage building point cloud large-scale denoising

The DBSCAN algorithm was applied to the density-based clustering of 3D point clouds. The specific methodology involves identifying clusters based on the density within spatial data. This approach classifies the data points into core, border, and noise points according to their density. Clusters are formed by connecting core points with sufficient density. A noteworthy feature of this algorithm is that it does not require pre-specification of the number of clusters. It is applicable to clusters of various shapes and sizes and is particularly effective in datasets with significant variations in density.

Noise can be identified by calculating the point cloud count in each cluster and comparing it with a threshold. Clusters with point cloud counts below the threshold were recognised as heritage architectural information clusters; otherwise, they were labelled as noise clusters (Fig. 7).

Fig. 7

The principle of denoising using the DBSCAN algorithm.

In this study, the DBSCAN algorithm was applied to distinguish the clustering patterns in heritage architectural point clouds. The specific applications of the algorithm are as follows: DBSCAN clustering was implemented in the Visual Studio software, and the code involved three header files: DBSCAN kdtree.h, DBSCAN precomp.h, and DBSCAN simple.h, and one source file: pcl cluster.cpp. In the design of the DBSCAN algorithm project, a Kd-tree was used to accelerate the testing of DBSCAN, and clustering extraction was performed using the Euclidean distance.

In this experiment, the following parameters were set. We set the cluster tolerance, minimum cluster size, and maximum cluster size.

Applying the DBSCAN algorithm to both individual heritage buildings and their interior furniture sections can effectively distinguish sparse point clouds, thereby contributing to further segmentation and denoising (Fig. 8).

Fig. 8

Performing DBSCAN algorithm for noise segmentation using visual studio software.

Point cloud density clustering based on CloudCompare software can also be used to analyse the density characteristics of point cloud data. Through clustering methods, points in the point cloud data can be grouped according to density differences, enabling the identification of regions with varying densities. By analysing the density-based groupings, abnormal points and isolated point cloud data can be identified, facilitating more efficient processing of large-scale point cloud datasets and improving data quality (Fig. 9).

Fig. 9

Intensity (left) and surface density (right) visual representation.

Heritage building point cloud small-scale denoising

Statistical filtering for denoising

The statistical analysis method employed here is the SOR filter, which is an effective method to address noise situations outside complex and concave-convex structures. An SOR filter is primarily used to remove outliers by identifying and filtering outliers that deviate from the overall data distribution.

The SOR filter typically relies on statistical measures such as the mean and standard deviation to identify and remove data points that deviate significantly from the average level. This is applicable in scenarios where noise or outliers must be eliminated but thresholds or rules must be predefined to determine what an outlier is. CloudCompare uses a point-cloud library (PCL) to eliminate SOR. This method assumes that the distance between a given point and its neighbouring points follows a normal distribution²³.

The denoising process using statistical filtering is as follows: The point cloud, which required denoising, was input into the statistical filter. The neighbourhood search points, K, were set for statistical filtering. The average distance from each query point to its K neighbouring points was calculated for denoising. The standard deviation of multiple standards was set. The average and standard deviation of the average distances were calculated for all the data points. The filtering range for outlier points was determined based on the average and standard deviation, providing the conditions for outlier point filtering. The outlier points were filtered, and the denoised point cloud and noise points were saved. A visualisation module was used to observe the denoising effect. If the denoising effect was unsatisfactory, the parameters were adjusted, and the statistical filtering operation was repeated (Figs. 10 and 11).

Fig. 10

Applying the SOR algorithm for denoising the arch (before and after denoising).

Fig. 11

Comparison of surface density Gaussian distribution histograms.

Using CloudCompare software, the ‘Number of points to use for mean distance estimation’ was set to 6, and the ‘Standard deviation multiplier threshold (nSigma)’ was set to 1. The formula for calculating the maximum distance is Max distance = average distance + nSigma × standard deviation.

From the analysis of the histogram and table, it is evident that the number of points within the range of 0–50,000 decreases after denoising with the SOR, indicating the removal of noise from the sparse point clouds (Table 1).

Table 1 Surface density Gaussian distribution analysis

Using the SOR algorithm for calculation, the ‘Number of points to use for mean distance estimation’ was set to 6 and the ‘Standard deviation multiplier threshold (nSigma)’ was set to 3, and the experimental result was B. Using the SOR algorithm for calculation, the ‘Number of points to use for mean distance estimation’ was set to 6 and ‘Standard deviation multiplier threshold (nSigma)’ was set to 2, and the experimental result was C (Fig. 12).

Fig. 12

Denoising using the SOR algorithm.

Before applying the SOR operation, the point counts for the platform were 6,609,706, for B it was 6,507,447, and for C it was 6,287,515. According to the histogram, a variation in the point count between B and C was observed in sparse areas, whereas the number of points in high-density regions remained relatively unchanged. From the experimental results, it can be concluded that the SOR algorithm is effective in denoising the overall sparse point clouds and marking data points that deviate significantly from the average distance as outliers. However, it may not be suitable for larger scenes because the results may inadvertently remove point clouds from other structures.

From the experimental before-and-after comparison, it is evident that points with sparse density and large interpoint distances were removed by SOR filtering. This method was particularly useful for point cloud models uniformly acquired through laser scanning. However, parts of the model where the laser scanning was uneven were prone to algorithmically removing points that were not outliers. The standard deviation and class values in the surface density gaussian distribution can be compared through SOR experiments B and C, as detailed in Table 2.

Table 2 Surface density Gaussian distribution

The above tests show that directly applying the SOR method does not effectively remove noise points from large-scale heritage building point clouds. It is necessary to segment the heritage building point cloud model using the method in Step 1. Then, noise point analysis should be performed as outlined in Step 2, followed by applying the SOR algorithm to denoise the square in front of the main hall (Fig. 13).

Fig. 13

Multiscale hierarchy denoising method.

For denoising small architectural component point cloud models, the SOR algorithm can effectively separate discrete points. For instance, in the point cloud model of the table inside the great achievement palace, discrete points are present around the table’s decorations and along the sides of the table. The desk at the great achievement palace was chosen for the before-and-after denoising comparison. The ‘Number of points to use for mean distance estimation’ was set to 6 and the ‘Standard deviation multiplier threshold (nSigma)’ was set to 3. The intensity value changes before and after the SOR denoising were analysed (Fig. 14).

Fig. 14

Visualisation comparison of point cloud intensity before and after SOR filtering for the desk.

Through SOR algorithm calculations, the noise on and around the desks in The Great Achievement Palace was effectively removed. For uniformly dense point cloud models or small-volume point cloud models, the SOR algorithm performed well at removing noise and outliers (Fig. 15).

Fig. 15

Intensity value histogram before and after SOR filtering.

The surface density was calculated using the same parameters. Visualisations and Gaussian distribution histogram changes were analysed before and after denoising the table (Figs. 16 and 17).

Fig. 16

Visualisation of point cloud surface density before and after SOR filtering for the desk.

Fig. 17

Histogram of point cloud surface density before and after SOR filtering for the desk.

Bilateral filtering denoising

Bilateral filtering and its variants apply the same parameters to all points in the heritage architectural point cloud. This leads to the insufficient or excessive smoothing of data with rich geometric structures (corners, smooth features, and sharp edges) and various noise intensities. Therefore, using the same parameters to process all the points in a noisy point cloud was inappropriate (Figs. 18 and 19).

Fig. 18

Intensity visualisation of denoising using bilateral filtering on the arch structure.

Fig. 19

Histograms of intensity changes and intensity Gaussian distribution before and after bilateral filtering.

In bilateral filtering, two main parameters must be configured: Spatial sigma, which is the variance of the normal distribution for the spatial part of the filter, and scalar sigma, which is the variance of the normal distribution for the scalar part of the filter. Setting spatial sigma to 0.03 and scalar sigma to 0.25 results in A. Setting spatial sigma to 0.03 and scalar sigma to 0.5 results in B. From the analysis of the charts, it can be observed that bilateral filtering has a visual impact on complex heritage architectural point cloud models (Table 3).

Table 3 Intensity Gaussian distribution analysis

When the parameters are set to (0.01, 80,000), the result is C; when they are set to (0.03, 80,000), the result is D.

Visualisation inspection and histogram analysis show that bilateral filtering, when applied to complex architectural heritage structures such as arches, has no effect on sparse point clouds. The point count remains unchanged before and after bilateral filtering, and the surface density remains constant. However, the smoothness of the model surface was altered, with higher values for bilateral filtering, resulting in increased smoothness (Figs. 20 and 21).

Fig. 20

Surface density visualisation.

Fig. 21

Surface density histogram using bilateral filtering.

Utilising bilateral filtering for point cloud denoising can maintain the sharpness of the edge contours³⁴ These sections can be denoised effectively through the bilateral filtering of flat areas such as walls and floors (Table 4).

Table 4 Surface density histogram analysis

Results

In this study, the point cloud model denoising the representative Great Achievement Palace of ancient Chinese official architecture was conducted. The multiscale hierarchy denoising method was applied to improve the quality of heritage building point clouds (HBPC) and was implemented in three distinct phases. The first phase involved hierarchical segmentation of the heritage building point cloud based on its structural features. Three key algorithms were used: the cloth simulation filter (CSF), Pass-through filter, and Slope filter. The CSF method effectively distinguished ground points from non-ground points, especially in complex terrains such as steep slopes and flat areas, providing a clearer dataset for further processing. The pass-through filter was applied to remove unnecessary points based on specific size thresholds, which is suitable for segmenting point cloud models of ancient Chinese official architectural structures, such as foundations, columns, and bracket sets. Additionally, the Slope filter algorithm was employed to identify and remove noise points from inclined surfaces by analysing the point cloud slope, such as the roof or ground of heritage buildings.

The second phase involves large-scale denoising, where the density-based spatial clustering of applications with noise (DBSCAN) algorithm was used to identify clusters in the point cloud and distinguish noise from structural elements. This method has proven effective for large or structurally complex heritage buildings, allowing for the separation of architectural details from noise. The DBSCAN algorithm is fine-tuned by adjusting parameters such as Cluster Tolerance, Min Cluster Size, and Max Cluster Size, depending on the size and density of the point cloud. Additionally, the built-in density clustering method of CloudCompare was employed, utilising parameters, such as surface density and local neighbourhood radius to further optimise clustering and remove noise from regions with inconsistent density.

The third phase, small-scale denoising, applied the statistical outlier removal (SOR) filter to eliminate sparse outliers based on statistical analysis of mean distance and standard deviation. This has been proven effective for preserving fine details of small architectural structures. As shown in Fig. 13, after Feature Structural Hierarchical Segmentation and Large-scale denoising of the Great Achievement Palace platform point cloud model, small-scale point cloud outliers were denoised using the SOR method. Finally, a bilateral filter was applied to smooth the point cloud while preserving edge details, which is crucial for maintaining the integrity of heritage buildings.

Table 5 summarises the multiscale hierarchy denoising method, including the denoising techniques and their corresponding algorithm characteristics, the applicable range for buildings and components, and the parameter settings. This provides a reference for denoising point cloud models of ancient Chinese official architecture.

Table 5 Summary of the multiscale hierarchy denoising method

Conclusion

This study explored the concept of structural denoising while investigating a technique for denoising point cloud models with complicated historic architectures, which improves the quality of the collected data. The evaluation analysis revealed that a single algorithm could not effectively remove noise points of various scales generated during the data acquisition process of point clouds, especially in the case of point cloud models of complicated heritage architectures. Employing different denoising algorithms based on the structural area where the noise points are located can effectively eliminate noise, ensure the precision and quality of the heritage architecture point-cloud models, and restore the true geometric characteristics of the point-cloud data.

A structural hierarchical denoising approach was proposed as a foundation of this study. Initially, the point clouds of heritage buildings were categorised by structural layers. Methods such as CSF, slope filtering, and pass-through filtering were used to segment the heritage building point cloud models into different structural areas. Subsequently, large-scale point cloud model denoising was performed. Using the DBSCAN algorithm and cluster density conditions, we analysed whether sparse point clouds were noise points or outliers. Small-scale point cloud model denoising was then conducted by removing noise from low-density, small-volume point clouds using the SOR method. Finally, bilateral filtering was applied to smooth the surface point clouds of buildings and preserve the architectural structure contours. Experiments demonstrate the feasibility of this approach.

This method contributes to enhancing the precision and quality of heritage building point cloud models, allowing the highlighting of details and the acquisition of more consistent surface features. This facilitates subsequent data processing in modelling- and visualisation-related applications. Therefore, the hierarchy denoising method proposed in this study is of significant value for acquiring accurate point cloud information on heritage buildings. Although the new method has demonstrated good feasibility in experiments, it is recommended to further integrate it with more practical heritage preservation projects to validate its stability and applicability in complex environments.