Introduction

Painted pottery, as an ancient art form, embodies rich historical and cultural connotations as well as unique esthetic values. Painted pottery typically consists of a ceramic body and a painted layer. The pigments and binding materials forming the painted layer are prone to degradation due to complex chemical reactions and physical interactions, resulting in poor stability. The painted layer may suffer wear and tear from external friction, impact, and environmental contamination; pigment particles are susceptible to oxidation in humid conditions, leading to fading or discoloration. Additionally, the binding materials gradually decompose and fail due to the passage of time and the influence of water in burial environments, causing pigment detachment. The covering and penetration of soil from burial environments further obscure the painted layer. Such deterioration not only alters the appearance of pottery but also complicates the interpretation of patterns and symbols on its surface. Limited by image quality and other factors, these features may not be clearly visible, making accurate identification and extraction of information from the pottery surface challenging. Therefore, based on the concepts of cultural heritage conservation and restoration, it is imperative to develop efficient, nondestructive methods for extracting and enhancing key features in images, providing valuable references for subsequent restoration work1,2.

Spectroscopic analysis techniques are widely used in cultural heritage conservation to analyze material composition, identify pigment types, and study structural features. However, these techniques are constrained by sample size, surface flatness, and, in some cases, the need for sampling. Raman spectroscopy, for instance, provides highly detailed molecular structural information but is limited by its small spot size, making it unsuitable for large artifacts. Digital image analysis offers comprehensive spatial information but is restricted to the visible spectrum, significantly lacking in coverage of the near- and mid-infrared wavelengths3,4. Hyperspectral imaging (HSI) technology, through noninvasive methods, rapidly acquires detailed spectral information and spatial distribution of samples. It provides a comprehensive foundation for qualitative and quantitative analysis of materials, offering tremendous advantages and potential in the field of cultural heritage conservation5,6,7.

HSI has been applied in various cultural heritage studies. Alessia Candeo proposed a Fourier transform-based hyperspectral camera, demonstrating its robust field investigation capabilities for museum and archeological contexts by enhancing the dynamic range and illumination system8. The National Research Council of Italy—Institute of Optics developed a visible-near-infrared multispectral scanner prototype to analyze Manet’s painting Madonna of the Rabbit. By integrating X-ray fluorescence imaging, the study characterized pigment chemical and spatial properties. Spectral correlation mapping and artificial neural network algorithms were used to generate pigment distribution maps, enhancing the visibility of restoration marks and underdrawings9. At Tianjin University, Malina used HSI to capture information from painted patterns on the second bronze chariot unearthed from the Mausoleum of Qin Shihuang. By leveraging spectral and edge information from the near-infrared region, the team discovered and reconstructed the chariot’s surface patterns10. In China’s National Museum, Yang Qin and Ding Li used HSI to study the Yuan Dynasty painting Landscape in Misty Rain. By analyzing spectral features of seals and background elements, they proposed an index for enhancing blurred seal information and compared results using PCA and minimum noise fraction transformation methods11. Giovanna Vasco and Hélène Aureli introduced a simplified protocol combining HSI with PCA and classification methods for nondestructive analysis of cultural heritage paintings, integrating XRF, UVL, and IRR data to optimize large-scale collection characterization12.

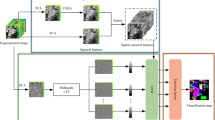
However, traditional methods like PCA13,14 and MNF15, as well as relying solely on true-color images, face challenges in comprehensively reflecting artifact details due to limited spectral bands, potentially leading to information loss. To address these challenges, we propose a novel method combining forward and inverse PCA transformations to obtain true-color images and leveraging SMACC16 to extract feature endmembers for generating enhanced images. PCA is used to reduce dimensionality, selecting principal components with the highest contribution rates. This step effectively retains key feature information while minimizing noise and redundant data. SMACC is then applied to extract endmembers from the PCA-processed images, exploiting its ability to capture intricate details, including subtle features that persist after PCA processing. By integrating PCA’s global feature extraction capabilities with SMACC’s local extraction strengths, this multilayered approach improves the accuracy and precision of feature extraction. Finally, enhanced and true-color images are fused in the HSV color space to optimize feature visualization. The specific flowchart is shown in Fig. 1.

Fig. 1
figure 1

Flowchart of the image enhancement process.

Full size image

Methods

Acquisition system

In this study, we utilized the iSpecHyper-VS1000 hyperspectral camera from Laisen Optics for data acquisition. The camera operates within a spectral range of 380–1020 nm, featuring 300 channels with a resolution better than 2.5 nm and a transverse scanning angle of less than 60°. The system is primarily composed of a halogen line light source (spectral range of 350–2500 nm, power of 300 W), a hyperspectral camera, an imaging lens (field of view angle of ±7°), and a personal computer integrated with acquisition control software. This setup is suitable for hyperspectral image acquisition of objects in a laboratory environment. After multiple trials, we set the parameters, including an integration time of 25 ms, resulting in clear and undistorted images. The acquisition system setup is illustrated in Fig. 2.

Fig. 2
figure 2

Experimental platform.

Full size image

The sample collected for this experiment is the lid of a Han Dynasty painted gray pottery pot with a ring handle, excavated from the Zhaojiaozui site in Yunyang. Upon observation, we noted that the painted pattern on the lid resembles a cloud motif. However, due to paint detachment and a substantial amount of soil on the surface, the pattern information has become very blurred, as shown in the sample pottery in Fig. 3. We selected a region with relatively distinct cloud motifs, region 1, as shown in Fig. 3b, for subsequent processing.

Fig. 3: Han dynasty painted gray pottery lid with selected cloud pattern area.
figure 3

a Han dynasty painted gray pottery lid with selected cloud pattern area. b Cloud-pattern region 1. c Cloud-pattern region 2.

Full size image

Data acquisition and preprocessing

Due to the indoor setting of this experiment, the influence of atmospheric radiation on the results can be considered negligible. However, the spectral curves captured by the hyperspectral camera reflect the light intensity values of each pixel, represented as DN. These DN values not only contain the information we need regarding the pottery samples but are also affected by instrument noise. Additionally, variations in the illumination angle can influence the collected DN values, thereby reducing the reliability and consistency of the data. To mitigate these effects, reflectance correction is necessary prior to data processing for the acquired hyperspectral images. The purpose of reflectance correction is to convert DN values into true spectral reflectance, eliminating interference from external lighting and instrument noise. The correction formula is as follows:

$$R{ef}=\frac{({R}_{D{ata}}-{R}_{B{lack}})}{{(R}_{{White}}-{R}_{{Black}})}$$
(1)

where Ref represents the corrected reflectance data, RData represents the raw collected data, RBlack represents the data collected under a black reference condition, and RWhite represents the data collected from a white reference. The spectral curves of the pottery lid before and after reflectance correction are shown in Fig. 4.

Fig. 4: Comparison of reflectance correction for the pottery lid.
figure 4

a Average spectra of various materials on the pottery lid before reflectance correction. b Average spectra of various materials on the pottery lid after reflectance correction.

Full size image

As shown in Fig. 4, after reflectance correction, the spectral curves of different pottery categories exhibit considerable noise at both ends of the spectral range (i.e., the beginning and the end), with limited usable information in these regions. This is primarily due to the low sensitivity of the hyperspectral camera in these bands. Therefore, to improve data quality, reduce errors caused by noise, and ensure the accuracy of subsequent analyses, we have decided to discard the first 40 and the last 40 bands, retaining only the effective data within the range of 440–960 nm.

PCA is first applied to reduce the dimensionality of hyperspectral data while preserving its major variance features. The process involves computing the covariance matrix of the spectral data, as shown in Eq. (2):

$$C=\frac{1}{n-1}{X}_{std}^{\top }{X}_{{std}}$$
(2)

An eigenvalue decomposition is then performed to select the principal eigenvectors (i.e., the principal components). The eigenvalues and corresponding eigenvectors of the covariance matrix are calculated as Eq. (3):

$$C{v}_{i}={\lambda }_{i}{v}_{i},i=1,2,\ldots ,d$$
(3)

Here, \({\lambda }_{i}\) represents the eigenvalues of the covariance matrix, arranged in descending order (\({\lambda }_{1}\ge {\lambda }_{2}\ge \ldots \ge {\lambda }_{d}\))and \({v}_{i}\) denotes the corresponding eigenvectors. The eigenvalues indicate the variance explained by each principal component, while the eigenvectors define the directions of the principal components in the original feature space. The decomposition of eigenvalues and eigenvectors reveals the principal directions of the data, i.e., the principal components. Based on the magnitude of the eigenvalues, the top \(k\) eigenvectors corresponding to the largest eigenvalues are selected to form the new principal component matrix \({V}_{k}\in {{\mathbb{R}}}^{d\times k}\) which is then used to reconstruct the image. This approach proves particularly effective for hyperspectral images characterized by high redundancy and noise. By calculating the contribution rate of each principal component, it becomes possible to identify the components most significant in representing the overall characteristics of the data. This further enables dimensionality reduction and optimization of subsequent analysis. The contribution rate of each principal component is calculated as shown in Eq. (4):

$$CR=\,\frac{{\lambda }_{i}}{{\sum }_{i=1}^{n}{\lambda }_{i}}$$
(4)

Where\(\,{\lambda }_{i}\) represents the eigenvalue of the ith principal component, CR represents the contribution rate of the principal component,\({\sum }_{i=1}^{n}{\lambda }_{i}\) represents the total sum of the eigenvalues of all principal components. The contribution rate of the principal components measures the extent to which each principal component contributes to the total variance, with higher values indicating a stronger ability of the component to explain the variability of the original variables.

However, manually annotating homogeneous regions is both challenging and prone to subjective errors. Therefore, this study adopts the SVM17 as the classification tool. The fundamental concept of SVM is based on the principle of structural risk minimization. By constructing an optimal separating hyperplane that maximizes the geometric margin between different sample data, SVM enhances the generalization capability and robustness of the classification model. Under ideal conditions, when the sample data are linearly separable, the decision boundary that maximizes the inter-class margin can be determined by solving the objective function, as shown in Eq. (5).

$$\mathop{\min }\limits_{\omega ,b,\xi }\frac{1}{2}{{||}\omega {||}}^{2}+C\mathop{\sum }\limits_{i=1}^{n}{\xi }_{{\rm{i}}}\,{\rm{s}}.{\rm{t}}.\,{y}_{i}\left({\omega }^{T}{x}_{i}+b\right)\ge 1-{\xi }_{i}\,,{\xi }_{i}\ge 0$$
(5)

Here, \(\omega\) denotes the weight vector, \(b\) is the bias term of the hyperplane, \({\xi }_{i}\) represents the slack variables that allow violations of the hard-margin constraint, and\(\,C\) is the regularization parameter.

In HSI, each pixel often contains a mixture of multiple materials due to the limited spatial resolution, resulting in the “mixed pixel” effect. To address this, we adopt the SMACC algorithm to extract spectrally pure endmembers from the data. SMACC iteratively constructs a convex cone in the spectral space using previously selected endmembers and identifies the next endmember by maximizing the angle between the candidate pixel and the existing convex cone. This process continues until a specified number of endmembers are extracted or the angular threshold is met. The extracted endmembers are used to characterize distinct pigment types on the pottery surface. These endmembers are further evaluated using Spectral Angle Distance (SAD) and Spectral Information Divergence (SID) to determine their similarity to known pigment spectra. The selected optimal endmember is then used to guide the enhancement of specific image regions. These methods form a complete pipeline for hyperspectral image processing and feature enhancement in this study.

Results

Feature extraction of the Han dynasty polychrome pottery lid

We preprocessed the spectral data of the hyperspectral images collected in the experiment by removing the first 40 and last 40 bands, which contained high noise and limited useful information, retaining spectral data in the range of 440–960 nm. The retained spectral data were subjected to PCA transformation18,19. PCA is a technique widely used for image enhancement, with applications in denoising, contrast enhancement, and color enhancement20,21. Its advantages lie in effectively reducing dimensionality, compressing images, removing noise, and extracting primary features for subsequent processing22.

We selected the cloud pattern area 1 of the Han Dynasty-painted gray pottery lid with a ring handle as the processing target. The results after PCA processing are shown in Table 1. By summing the variance contribution rates of the first five components, we found that the first five principal components explained 99.81% of the total variance of the original hyperspectral image, while the last two principal components accounted for only 0.0183%. Based on this assessment, we determined that the first five principal components contained the main information of the image. We then used these five principal components for inverse transformation to remove redundant information and enhance the quality of the original image. The images of the first five principal components are shown in Fig. 5.

Fig. 5: Principal component images of cloud pattern area 1.
figure 5

a Principal component 1. b Principal component 2. c Principal component 3. d Principal component 4. e Principal component 5.

Full size image
Table 1 Eigenvalues and information content of each principal component
Full size table

After converting the hyperspectral image into a true-color image, it is necessary to classify the image in order to extract the average spectral curves of each homogeneous region. To capture nonlinear decision boundaries, the Radial Basis Function kernel was selected, which is well-suited for handling complex, nonlinear data separation problems. Specifically, the kernel parameter \({\rm{\gamma }}\) was set to 0.005, and the penalty parameter \(C\) was set to 100. A lower\(\,{\rm{\gamma }}\) value implies that each training sample has a broader influence, resulting in smoother decision boundaries and better generalization. In contrast, a higher \(C\) value leads to a tighter fit on the training data with narrower margins. These parameter values were chosen to strike a balance between generalization and fitting accuracy, ultimately yielding a classifier that effectively distinguishes pigment types while maintaining robustness on unseen data. We selected the ROI, namely the cloud pattern area, for SVM classification. After removing noisy spectral bands, the resulting dataset had dimensions of 85 × 77 × 220. Each pixel was treated as an individual sample, yielding a total of 6545 samples. The dataset was divided into training and testing subsets at a ratio of 8:2, resulting in 5236 training samples and 1309 testing samples. In practical application, fivefold cross-validation was performed on the labeled samples to further optimize the parameters and ensure good model performance on unseen data.

Research conducted by museum staff on the Han dynasty-painted gray pottery vessel lid revealed the pigment distribution structure shown in Fig. 6. The Han dynasty-painted gray pottery vessel lid features a gray-black body, coated with a uniform layer of white pigment as the base color. Subsequently, black and red pigments were used to depict the cloud pattern areas. After SVM classification, we accurately delineated these regions of different pigments, obtained labeled data for each region, and calculated their average spectral curves, resulting in the labeled data processed by SVM as shown in Fig. 7.

Fig. 6
figure 6

Pigment distribution structure of the Han dynasty painted gray pottery lid.

Full size image
Fig. 7: SVM classification results for the cloud pattern region on the Han dynasty painted gray pottery lid.
figure 7

a Han dynasty painted gray pottery lid with selected cloud pattern area. b Cloud-pattern region 1. c SVM classification results.

Full size image

We applied S-G filtering23,24 to smooth the average raw spectral curves obtained after SVM processing, aiming to provide a more reliable and stable data foundation for subsequent analysis. Using the S-G filtering technique, we successfully removed noise and unnecessary fluctuations from the raw spectral curves. Figure 8a shows the spectral curves of five different substances, while Fig. 8b presents the smoothed spectral curves of these substances after S-G filtering. Figure 8c shows the reflectance curve of the 0.2 reflectance gray board under the same conditions.

Fig. 8: Comparison of spectral curves before and after S-G filtering.
figure 8

a Spectral curves of five types of materials. b Spectral curves of five types of materials after S-G filtering. c Reflectance curve of the 0.2 reflectance gray board.

Full size image

In HSI, due to the high spectral resolution, a single pixel (referred to as a pixel element) often consists of multiple components, a phenomenon known as the “mixed pixel” effect. The SMACC algorithm attempts to identify the pure endmembers that constitute the mixed pixels and their abundances25. After processing with SMACC, we compared the extracted spectral lines with the spectral data of the cloud pattern region classified by SVM, using SAD as in Eq. (6) and SID as in Eq. (7) to measure the similarity between two spectral vectors18,19,26. Smaller SAD and SID values indicate greater spectral similarity.

$${SAD}\left(u,v\right)=\arccos \left(\frac{\left(u\cdot v\right)}{\mathrm{||}u||\cdot ||v\mathrm{||}}\right)$$
(6)
$${SID}\left(u,v\right)=\sum _{i}\left({p}_{u}\left(i\right)\log \frac{{p}_{u}\left(i\right)}{{p}_{V}\left(i\right)}+{p}_{V}\left(i\right)\log \frac{{p}_{V}\left(i\right)}{{p}_{U}\left(i\right)}\right)$$
(7)

Where u and v are two spectral vectors, pu(i) and pv(i) are the normalized probability distributions of the spectral vectors u and v at the it band, respectively.

We selected endmembers with high similarity to each homogeneous region as the basis for feature extraction of each region, serving as the objects for subsequent processing to determine the spectral characteristics of different substances. The distance between endmembers reflects the differences between substances; the closer the endmembers, the higher the similarity to a particular substance, indicating that the endmember can effectively represent that substance. The abundance maps and endmember spectral curves obtained after SMACC processing are shown in Fig. 9.

Fig. 9: SMACC endmember extraction images and endmember spectral curves.
figure 9

a Abundance of telomere 1. b Abundance of telomere 2. c Abundance of telomere 3. d Abundance of telomere 4. e Abundance of telomere 5. f Endmember spectrum.

Full size image

We calculated the image evaluation indicators such as average gradient, information entropy, and spatial frequency for the feature endmember band images of the selected region27,28. The results are shown in Table 3.

According to the SAD and SID results in Table 2, it is evident that the spectral angle distance (0.0779) and spectral information divergence (0.065) between the red-painted curve of cloud pattern region 1 and endmember 5 are the smallest among the five endmembers. This indicates that the spectral vector of endmember 5 is most similar to the spectral data of the red painted region. Additionally, as seen from Table 3 and Fig. 9, the evaluation indicators of endmember 5 are significantly higher than those of endmember 4 and endmember 2. Given that endmember 2 has substantial image noise, endmember 5 was ultimately chosen as the optimal endmember for extracting the pottery line features.

Table 2 Similarity evaluation of red painted spectra and endmember spectral curves in cloud pattern area 1
Full size table
Table 3 Comparison of endmember image metrics
Full size table

To enhance the image features of the red regions, we first jointly processed the RGB true-color image obtained via inverse PCA transformation and the red feature mask extracted using the SMACC algorithm. The red feature mask was normalized to a range between 0 and 1. Subsequently, the RGB image was converted into the HSV color space, separating the hue (H), saturation (S), and value (V) channels. To prevent color distortion, the H channel was kept unchanged, while the S and V channels were enhanced by adding the normalized red feature mask. The enhanced HSV image was then converted back into the RGB color space, resulting in a pseudo-color image with significantly enhanced red regions, as shown in Fig. 10.

Fig. 10: Comparison of HSV feature-enhanced images.
figure 10

a Red feature extraction image. b PCA RGB image. c Feature enhanced image.

Full size image

Discussion

We first applied PCA to the original true-color image and selected the top five principal components with the highest contribution rates. These five components were then subjected to inverse PCA transformation to reconstruct the RGB format image, resulting in a PCA-enhanced image that preserves major feature information while reducing noise (as shown in Fig. 11c). Next, the SMACC algorithm was used to extract the red feature endmember from the PCA-enhanced image, generating a red feature mask (Fig. 11a). This mask was used to enhance the S and V channels of the HSV image, thereby increasing the saliency of red regions and producing an enhanced pseudo-color image (Fig. 11b). To further integrate the enhanced pseudo-color image with the true-color image obtained through inverse PCA, a multi-scale image fusion method based on the Laplacian pyramid was employed. Gaussian pyramids were first constructed for both input images, followed by computation of the corresponding Laplacian pyramids to obtain image detail layers at different scales. A weighted average fusion strategy was applied to each layer of the Laplacian images. In the red feature regions, the weights were set to 0.7 for the enhanced pseudo-color image and 0.3 for the true-color image. The fusion formula is as shown in Eq. (8):

$${L}_{{fused}}={\omega }_{1}\times {L}_{{en}h{anced}}+{\omega }_{2}\times {L}_{{PCA}{truecolr}}$$
(8)
Fig. 11: Comparison of feature-enhanced images.
figure 11

a Red feature extraction image. b Feature enhanced image. c PCA RGB image. d Fused image.

Full size image

Here, \({\omega }_{1}\) and \({\omega }_{2}\) represent the fusion weights for the enhanced pseudo-color image and the true-color image, respectively. Based on the fused Laplacian pyramid, the image was reconstructed from top to bottom, resulting in the final feature-fused image (as shown in Fig. 11d). The fused image exhibits overall improvements in color, brightness, and sharpness, with significantly enhanced features in the red regions.

Based on the data analysis results presented in Table 4, it is observed that the image processed with the feature enhancement algorithm shows significant improvements in key quality evaluation indicators—average gradient, spatial frequency components, and information entropy—compared to the true-color image enhanced solely by PCA. This distinction underscores the notable efficacy and potential of our method in enhancing the visual effect and information content of the images.

Table 4 Comparison of enhanced image metrics
Full size table

In this study, we successfully combined PCA and SMACC algorithms to enhance the visual representation capabilities of hyperspectral images and highlight obscure features on pottery. Preliminary results show that images processed with PCA exhibit more vivid colors and improved clarity in RGB conversion, while the SMACC algorithm effectively extracted endmember features from the PCA-enhanced image. When these endmember features were fused with the PCA true-color image in the HSV space, the resulting feature-enhanced image displayed better overall color brightness and clarity. Notably, the red region’s features were significantly enhanced. Compared to images obtained using PCA enhancement alone, the average gradient, spatial frequency, and information entropy of the feature-enhanced image increased by 22.23%, 30.46%, and 17.21%, respectively, which is crucial for cultural heritage preservation. Compared to previous research, this study not only theoretically broadens the application scope of HSI technology in cultural heritage conservation but also provides practical technical support for the restoration of ancient pottery.