Introduction

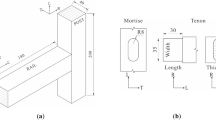
Historic buildings hold significant cultural, scientific, and aesthetic values, showcasing the achievements of past eras. China occupies a unique position in architectural history, boasting the world’s largest collection of preserved historic timber-framed buildings1. As a significant and iconic feature of classical Chinese architecture, the Tou-Kung joint interlocks layers of stacked wooden members into a cohesive structure using precise mortise-and-tenon joints2,3,4, as illustrated in Fig. 1. Historic wooden buildings often face fire risks due to their combustibility and high fire load5, presenting a significant challenge in heritage conservation6. Over time, weathering has caused considerable degradation of wood materials7, increasing the fire hazards of older wood-frame buildings. Despite the threat of fire, Tou-Kung joints are often capable of preserving the structural integrity of the main structure after a disaster, highlighting their structural toughness and significance. Protecting wooden Tou-Kung joints requires a combination of their constructional properties and their response to strong pressure8. Historical changes have led to variations in the construction forms of Tou-Kung joints across different eras, each characterized by its regulatory standards9. This variability makes it challenging to assess accurately and objectively assess the safety of Tou-Kung joints in historic wooden buildings. To begin with, it is essential to clarify the mechanisms underlying the crushing dynamics of wooden Tou-Kung joints.

Fig. 1: The description of a wooden historical building located in China.
figure 1

a Feiyun Pavilion; b The Tou-Kung of Dule Temple.

Full size image

The joints of Chinese wooden buildings, known as Tou-Kung, have been extensively studied in recent years. The existing studies primarily focus on several key areas: the investigation of basic mechanical properties10, the assessment of damage modes under loading11, the analysis of cooperative work mechanisms8,12,13, the examination of deformation and energy dissipation mechanisms14, and the enhancement and reinforcement of performance15,16. Additionally, these studies incorporate high-precision numerical simulations using the finite element analysis method17,18,19 and other related approaches. Preserving Tou-Kung joints is essential for maintaining the integrity of historic wood-frame buildings. As a significant part of China’s architectural heritage, the Tou-Kung has withstood the test of time and continues to serve its original purpose. Fire prevention in wood-framed historic buildings is crucial for preservation and has been extensively studied in recent years. Previous research examined the effects of laminating on the fire performance of wood samples20, the influence of hydrogen fluoride on wood surfaces21, and how traditional wood window air gap ratios affect vertical flame spread22. The main frame of an old wood-framed building can still be preserved and function after a fire. However, little is known about how different components in Tou-Kung joints affect safety and stability.

In the current work, loading tests under strong vertical pressure were carried out to clarify the performance of wooden Tou-Kung joints with different Ang members. Three samples of the Xia-Ang joint, Wu-Ang joint and Shang-Ang joint were used. Mechanical property analysis clarifies the response of different Ang components to the Tou-Kung joint as a whole. An image acquisition system was utilized to examine the failure modes of various components.

Methods

Typical configurations of the Tou-Kung joints

The Ang structure is a common type of the Tou-Kung joints found in traditional Chinese wooden buildings from the Song and Liao dynasties. Compared to other traditional Chinese joints from the Ming and Qing dynasties, the Tou-Kung joint has a relatively simple design and fewer components. Its structural elements are larger, and its primary function is to bear and distribute the loads from the roof. The Tou-Kung joint is integrated with the beams and columns of the timber structure and plays a vital role in maintaining the integrity of the timber frame structure.

Given the complex structure of the Tou-Kung joint. Since the criteria and terminology of its components have varied in different historical periods, it is necessary first to clarify its composition. The primary components of the Tou-Kung include the Dou, Gong, Ang and Fang, which can be categorized into five levels based on their spatial arrangement. These components are interconnected through mortise and tenon joints. Because Yingzao Fashi is the first secretary who specifies in detail the Tou-Kung system, rank, name, etc., this paper introduces the main features of the Tou-Kung following it, as shown in Fig. 2.

Fig. 2
figure 2

Configurations of Tou-Kung.

Full size image

The first layer consists of a large, bucket-shaped structure known as the Lu-Tou, positioned at the center of gravity of the bottom layer’s overall weight. The Lu-Tou features a cruciform opening through which all vertical loads are transmitted to the structure and connected to the column via a mortise and tenon joint for further support.

The second layer comprises Hua-Gong and Ni-Dao-Gong. Hua-Gong serves as the primary load-bearing bending component, positioned perpendicularly to the width of the building’s facade and extending outward from the interior. Ni-Dao-Gong, commonly referred to as a horizontal bending component, is characterized by its non-protruding nature.

The third layer comprises Ru-Fu, Xia-Ang, Bi-Nei-Man-Gong and Gua-Zi-Gong. Ru-Fu is between the front and back eave and inner columns. The ends of Ru-Fu rest on top of Tou-Kung and the tails are typically inserted into the inner column, which bears the weight of the roof and transfers it to the underlying beam and column structure. Ang is a diagonal component of the Song-style Tou-Kung joint. It helps create elongated eaves without raising their height by supporting them with a diagonal structure. Ang is a lever within the structure, utilizing Ni-Dao-Gong and Man-Gong as fulcrum points. The weight at the head of the Ang balances the roof’s overhang at its tail. Both Man-Gong and Gua-Zi-Gong belong to the category of horizontal bending components.

The fourth layer consists of Shua-Tou, Zhu-Tou-Fang (Si-Pu), Wai-Man-Gong, and Ling-Gong. Zhu-Tou-Fang is a wooden beam positioned on the Ni-Dao-Gong between the columns, structurally linking the left and right sides while facilitating communication between the upper and lower levels.

The fifth layer is composed of Chen-Fang-Tou, Li-Luo-Han-Fang (five layers), Zhu-Tou-Fang (five layers), Wai-Luo-Han-Fang (five layers), Ping-Qi-Fang and Liao-Yan-Fang. Chen-Fang-Tou is the uppermost layer of Fang wood aligned with the direction of Tou-Kung’s protrusion, resting on the back of Shua-Tou and connecting the various Fang components. Luo-Han-Fang is supported by either Gua-Zi-Gong or Man-Gong, enhancing the horizontal connection.

Besides these primary components, the Tou-Kung joint is interconnected by various smaller elements, such as San-Dou, Jiao-Hu-Dou, Qi-Fu-Dou, Qi-Ang-Dou and Qi-Xin-Dou. During the Song and Liao dynasties, these components were segmented into three vertical parts: the upper part Dou-Er, the middle part Dou-Ping, and the lower part Dou-Qi.

Design of Tou-Kung joints

Based on the location and function of the Ang structure within Tou-Kung joints, these joints can be categorized into three types: Xia-Ang Tou-Kung joints, Shang-Ang Tou-Kung joints, and Wu-Ang Tou-Kung joints. This study focuses on the Tou-Kung structures from three prototypes: the Main Hall of Longyan Temple in Lingchuan (Fig. 3a, b), the Sanqing Hall of Yongle Palace (Fig. 3c, d), and the Shanmen of Dule Temple (Fig. 3e, f). Vertical load tests were subsequently conducted to examine the vertical mechanical properties, ensuring that there was no overturning during the process.

Fig. 3: Several types of Ang structure of Tou-Kung joints.
figure 3

a, b Xia-Ang Tou-Kung of Longyan Temple, c, d Shang-Ang Tou-Kung of Yongle Palace, e, f Wu-Ang Tou-Kung of Dule Temple. a Main view of Xia-Ang Tou-Kung; b Top view of Xia-Ang Tou-Kung; c Main view of Shang-Ang Tou-Kung; d Top view of Shang-Ang Tou-Kung; e Main view of Wu-Ang Tou-Kung; f Top view of Wu-Ang Tou-Kung).

Full size image

A reduced-scale ratio of 1:10 was selected for the test specimens based on geometrical similarity and considering structural configurations, material properties, and testing conditions. Model similarity theory establishes a relationship between the mechanical properties of reduced-scale and full-scale models, derived through dimensional analysis. Six specimens were tested: two Xia-Ang Tou-Kungs, two Shang-Ang Tou-Kungs, and two Wu-Ang Tou-Kungs.

The test model was constructed using the illustrations in the Song Dynasty’s Yingzao Fashi, which served as the official construction standard for historic wooden buildings. This standard utilizes a system of materials and parts, where one unit is defined as 1 mm and is classified as first-class material to facilitate calculations and conversions. Table 1 presents the dimensions of the main components. The overall dimensions of the test model are 143 mm × 180 mm × 110 mm for the Xia-Ang structure, 153 mm × 144 mm × 110 mm for the Shang-Ang structure, and 166 mm × 126 mm × 110 mm for the Wu-Ang structure.

Table 1 Dimensions of main components of Tou-Kung
Full size table

Experimental device and loading program

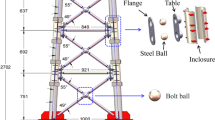
The experiments of these three groups of Tou-Kung joints were all displacement-controlled vertical forward-loading experiments. Figure 4 illustrates the experimental device used for the Tou-Kung joint. Three preloading cycles were conducted prior to formal loading to estimate the ultimate load capacity and calibrate sensor accuracy. The loading protocol consisted of two stages: pre-loading (0–5% Fmax) to eliminate assembly gaps, followed by quasi-static displacement-controlled loading at 0.04 mm/s, with cracks appearing until structural collapse. The displacement-controlled vertical forward loading was imposed by an electro-hydraulic servo actuator, which also could record the vertical displacements and the vertical loads during the loading process, and a loading sensor was placed between the loading rod and loading plate. A digital image correlation (DIC) system with a 50 mm focal length lens was employed to capture full-field strain distribution at a 2 Hz sampling rate, particularly focusing on stress concentration areas around the mortise-tenon joints. According to the analysis of the architectural forms, the structural configurations and the reduced-scale factor, the loading rate was taken as 0.04 mm/s. All tests were carried out until the specimen failed.

Fig. 4: Vertical load monotone loading test system.
figure 4

a Experimental device; b Experimental schematic; c Changes before and after sample loading.

Full size image

The Fang transfers the vertical load from the roof to the Tou-Kung in real buildings. In this experiment, to accurately simulate the mechanical behavior of the Tou-Kung joints under vertical loading, especially the role of the Ang structure, the complex actual force situation is simplified and the loading point is positioned at the fifth floor of the joint. The applied force and displacement changes were accurately and reliably collected and processed in real-time by the servo controller, force and displacement sensors, strain amplifiers and data acquisition instruments. A video camera recorded the entire loading process during the tests.

Determination of the mechanical characteristics

The initial stiffness ke, yielding load Fy, ultimate load Fu, maximum load Fmax and ductility D are determined by analyzing the load-displacement curve obtained from the test. The maximum load capacity is identified at the peak of the load-displacement curve. The limit points correspond to the displacements at which the load decreases to 80% of the maximum load. To determine the yield point, the Equivalent Energy Elastoplastic (EEEP) method23 is used to obtain Fy and Δy, which represent the yielding load and the corresponding displacement, respectively, as illustrated in Fig. 5b. The initial stiffness is defined by the slope of the secant line in the vertical load-displacement curve corresponding to 40% and 10% of the maximum load capacity24 and is calculated as follows:

$${k}_{e}=\frac{0.4{F}_{\max }-0.1{F}_{\max }}{{\Delta }_{0.4}-{\Delta }_{0.1}}$$
(1)
Fig. 5: Determination of characteristic points and yield points.
figure 5

a Methods for determining mechanical properties; b Determination of yield point.

Full size image

As the equivalent energy elastoplastic curve demonstrates, the yielding stage occurs when the component undergoes elastic damage and transitions into the plastic state. This stage is defined as follows25:

$${F}_{{\rm{y}}}=({\Delta }_{{\rm{u}}}-\sqrt{{\Delta }_{{\rm{u}}}^{2}-\frac{2A}{{k}_{{\rm{u}}}}}){k}_{{\rm{u}}}$$
(2)

where A represents the area bounded by the load-displacement curve between zero and the limit displacement. ku denotes the elastic shear stiffness, which can be defined as follows:

$${k}_{{\rm{u}}}=\frac{0.4{F}_{\max }}{{\Delta }_{0.4}}$$
(3)

Ductility serves as an indicator for measuring the plastic deformation of Tou-Kung joints. More excellent ductility implies a higher deformation capacity of the material after reaching its maximum load capacity without experiencing sudden failure. It is defined as follows26:

$$D=\frac{{\Delta }_{{\rm{u}}}}{{\Delta }_{{\rm{y}}}}$$
(4)

Results

Experimental phenomenon

The initial consolidation stage shows that, due to gaps between the components of the Tou-Kung joint, the system is compressed downward as a whole, causing the parts to come into contact without evident damage. The gaps are closed as loading continues, and the Tou-Kung joint begins to bear the vertical load. The Tou-Kung joint consists of components interconnected through tenons and mortises, which come in various forms and mechanisms—consequently, each component exhibits different failure modes.

Under vertical loading, the Lu-Tou is illustrated in Fig. 6a. All vertical loads are transferred to the Lu-Tou via the other components, making it the part that experiences the greatest compression. The maximum compressive stress in the Lu-Tou first exceeds the compressive strength, leading to plastic compressive deformation, which causes the Lu-Tou Dou-Qi to deform and the Dou-Ping to sag downward. As the load increases, the Dou-Er and Dou-Ping in the compression zone fracture under the combined effects of compressive and shear stresses, ultimately resulting in splitting.

Fig. 6: Diagram of main components after the experiment.
figure 6

a The Lu-Dou; b The Gong; c The Xia-Ang; d The Shang-Ang.

Full size image

Figure 6b shows the Gong under vertical load. As the primary bending component of the Tou-Kung joint, the Gong will undergo plastic compression deformation in the middle of it upon applying a vertical load. Owing to the high longitudinal tensile strength of wood along the grain, the Gong do not bend or break during the initial stages. However, with increasing load, the compressed area of the Gong in certain test specimens eventually fails.

Under vertical loading, the Xia-Ang structure is shown in Fig. 6c. Experimental observations indicate that the Ang is also subjected to bending and will experience bending deformation. However, since wood possesses high strength along the grain, significant bending failure is unlikely. At the base of the Xia-Ang structure, the vertical load is distributed among four compression areas, reducing the compressive stress in these regions. The transverse compressive stress remains below the compressive strength of the wood, allowing the Xia-Ang structure to stay intact throughout the test. In comparison to other components of the Tou-Kung joint, the Xia-Ang structure sustained more substantial damage on the first and second floors. The Xia-Ang structure concentrates damage at the San-Dou on subsequent layers by disrupting the regular layering of the Tou-Kung joint. This ensures that most of the main components remain undamaged even if the joint fails.

Under vertical loading, the Shang-Ang structure is depicted in Fig. 6d. The Shang-Ang structure is also a bending member that will undergo bending deformation. At the lower section of them, the vertical load is shared across three compression zones, reducing compressive stress in these areas. The compressive stress in the transverse direction is again less than the wood’s compressive strength, allowing the Shang-Ang structure to sustain its integrity until the end of the test. As vertical loading continues, the San-Dou on the third layer of the Bineiman-Gong begins to tilt. It results in the cracking of the second layer of Nidao-Gong and Hua-Gong, thereby causing the structure to disperse outward. The Jiaohu-Dou then disengages, leading to the failure of the joint. The Shang-Ang structure’s second, third, and fourth layers sustained the most severe damage compared to other components. The Shang-Ang structure is combined with Hua-Gong to support the overall structure at the joints. This enables vertical loads to be transmitted in four directions without overturning the structure.

The Wu-Ang structure directly transfers vertical loads downwards, tilting in different directions due to the varying grain orientations in the Lu-Tou base. As a result, it is the most unstable of the three Ang structures, with each component likely to sustain the most damage. Under vertical load, the primary failure modes of the Tou-Kung joint are compression splitting along the diameter of the Lu-Tou and plastic compression deformation and fracture perpendicular to the grain in the middle of the Gong and Fang.

Load-displacement curve analysis

The vertical load-displacement curve can be divided into five stages, as illustrated in Fig. 7: the initial consolidation stage (OA), the elastic stage (AB), the yielding stage (BC), the loading platform (CE), and the failure stage27. During the initial loading stage, the relationship between vertical load and displacement is approximately linear due to the gaps between the members in the Tou-Kung joint. These gaps gradually compress and close as the members come into contact. Vertical loads and displacements show a linear relationship when the wood remains elastic. The growth rate increases slightly. The material reaches the elastic deformation limit as the vertical load is applied. It begins to experience plastic deformation, thus entering the yielding stage, during which the Lu-Tou undergoes compression yielding. At this point, the increase in load becomes non-linear, and the growth rate of vertical displacement begins to decline significantly. As the Lu-Tou cracks, the Gong embedded within it bears most of the load, further reducing the growth rate of displacement. In the later stages of loading, the contact area between the Lu-Dou and Gong enters a hardening phase. As the load increases, the San-Dou begins to fail, ultimately leading to the collapse of the entire Tou-Kung joint and structural failure.

Fig. 7
figure 7

Typical load-displacement curve of Tou-Kung.

Full size image

Figure 8 compares the load-displacement curves of Tou-Kung joints under vertical load. “Xia-Ang TK”, “Shang-Ang TK” and “Wu-Ang TK” refer to the Tou-Kung joints of the Xia-Ang, Shang-Ang and Wu-Ang structures, respectively. A comparison of the load-displacement curves for Tou-Kung joints with different Ang structures reveals that they exhibit similar trends during the elastic stage. However, the test specimens display distinct load-displacement curves and other failure modes after that. The serrated characteristics of the curves originate from sequential wood fiber fracture events.

Fig. 8: Experimental load-displacement curves.
figure 8

a The Xia-Ang Tou-Kung; b The Shang-Ang Tou-Kung; c The Wu-Ang Tou-Kung.

Full size image

Based on the load-displacement curves derived from the tests, the initial stiffness, maximum load-bearing capacity, ultimate load and ductility of the Tou-Kung joints were determined and a statistical analysis of the results was conducted. Figure 9a shows the initial stiffness of the Tou-Kung joints. From the experimental results, the initial stiffness of the joint is higher for the Xia-Ang structure. This is because the Xia-Ang is more effective in transferring and distributing the vertical load in the structure, and its longer horizontal length and specific inclination angle make the joint work well together and resist the deformation better at the initial stage of the vertical load. In contrast, the initial stiffness of the Shang-Ang structure is the lowest. The shorter horizontal length and the position of the superstructure in the joint make its contribution to the overall stiffness relatively small when it is subjected to vertical loads, and the coordination of deformation among the members is weak.

Fig. 9: Typical mechanical properties of the Tou-Kung joints.
figure 9

a The change of initial stiffness; b The change of Maximum load capacity; c The change of Ultimate load; d The change of Ductility.

Full size image

Figure 9b, c compares the variation of load capacity of different Ang structures. The yield strength, peak strength and ultimate load capacity of the Xia-Ang structure under vertical loading are excellent. Its structural form allows the vertical load to be distributed more evenly to the members and reduces the local stress concentration, thus improving the overall load-carrying capacity. For example, the four compression zones at the bottom of the Xia-Ang rise effectively spread the load and reduce the compressive stresses in individual zones, allowing the structure to remain stable under larger loads. The load capacity of the Shang-Ang structure is relatively low, although its vertical load is also shared through multiple compression zones, but due to the short horizontal length, when transferring the upper load, the force cannot be effectively dispersed to the whole joint as in the case of the Xia-Ang, resulting in the premature reaching of the load limit of some members, which affects the overall load capacity. The Wu-Ang structure directly downward transmission of vertical loads, due to the differences in the direction of the grain of the wood at the bottom of the capital, the structural stability of the structure is poor, and the components are easily damaged, so its load capacity is comparable with the Shang-Ang structure, lower than the Xia-Ang structure.

Figure 9d analyzes the Tou-Kung joints in terms of ductility. The Shang-Ang structure exhibits the best ductility. Ductility reflects the ability of the joint to continue to deform without sudden damage after reaching its maximum load capacity. After the joint reaches the ultimate load, the Shang-Ang can still absorb a large amount of energy and keep the structure from sudden collapse through its deformation and the relative displacement between the members. This is mainly due to its structural form and the connection between the members, in the larger deformation, the members can collaborate to deform and delay the occurrence of damage. The ductility of the Xia-Ang structure is relatively poor due to its large initial stiffness. After the load reaches a certain degree, the members are prone to brittle damage, resulting in the performance of the ductility is not as good as that of the Shang-Ang structure. The ductility of the Wu-Ang structure is similar to that of the Xia-Ang structure, and in the process of structural damage, although the overall stability is poor, the interaction between the components also makes it have a certain deformation capacity, which can absorb energy to a certain extent, but the ductility performance is not as good as that of the Shang-Ang structure. Comprehensive view, different Ang structure on the joint stiffness, load capacity and ductility of the significant impact, in the protection and repair of ancient buildings, should fully consider these differences, according to the actual needs of the choice of appropriate structural form or targeted reinforcement treatment.

Vertical stiffness analysis

Figure 10 compares the vertical stiffness and displacement curves for three sets of Tou-Kung joints. During the loading process, the trend of the stiffness of each Ang structure varies with the increase of displacement. Due to the compression of the gap between the members of the joints and the plastic deformation of the wood, such as the splitting of the wood at the bottom of the capital, which leads to the plastic deformation of the embedded zone between the joint and the capital and enters into the hardening stage of the embedded zone between the capital and the joint after the cracks of the capital have been fully formed, the vertical stiffness will increase and then decrease, but there are differences in the turning point of the change in stiffness and the magnitude of the change of the different Ang structures. The Xia-Ang structure in the deformation of the initial growth of the stiffness is more obvious, and can be in the larger load range to maintain a relatively high stiffness; the Shang-Ang structure stiffness change is relatively more dramatic, in the structure of a small deformation, the stiffness may be a significant decline; the Wu-Ang structure of the stiffness of the change is relatively smooth.

Fig. 10: Comparison of three different Ang structures’ vertical stiffness and displacement curves.
figure 10

a The Xia-Ang Tou-Kung; b The Shang-Ang Tou-Kung; c The Wu-Ang Tou-Kung.

Full size image

Influence factors on the mechanical properties of the Tou-Kong joints

The three sets of Tou-Kung joint tests included variables such as the tilt angle of different Ang and the components’ horizontal length (L) and height (H). To examine the effects of these variables on load-bearing capacity, Table 2 presents the Pearson coefficients of correlation (PCC) between them and the ultimate load, maximum load-bearing capacity, yielding load, vertical stiffness and ductility.

Table 2 PCC values of the mechanical properties of the Tou-Kung for different factors
Full size table

The analysis reveals that the PCC values indicate the presence of both positive and negative correlations. Specifically, the PCC values of the ultimate load concerning the inclination angle of the Ang structure and member length are all greater than 0.70, suggesting that these factors significantly impact the ultimate load-carrying capacity. A similar trend is observed for the maximum load capacity. While a comparable trend is noted regarding the yielding load, the absolute PCC value for the slenderness ratio is below 0.50. The initial stiffness demonstrates a relationship with the slenderness ratio of the Ang structure; the corresponding absolute PCC values are 0.6265, whereas the remaining PCC absolute values are below 0.35. A PCC absolute value less than or equal to 0.39 indicates a weak relationship between the ductility of the node and the inclination angle and length of the Ang member.

Based on the PCC analysis results, the ultimate load, maximum load capacity and yielding load are fitted as functions of the most influential independent variables. As shown in Fig. 11, the values of the ultimate load, maximum load capacity and yielding load initially decrease and then increase with an increase in the tilt angle. Given that the PCC values between maximum load capacity and ultimate load and tilt angle are 0.81 and 0.82, there is a robust correlation between both the maximum load capacity and ultimate load on the tilt angle of the Ang structure. In Fig. 11c, the yielding load is correlated with the inclination angle and member length of the Ang structure. This is substantiated by the PCC value of 0.78 between the yielding load and the tilt angle and 0.69 between the yielding load and member length.

Fig. 11: Relation between the ultimate load, the maximum load, yielding load and the most vital independent variable.
figure 11

a Tilt angle and ultimate load; b Tilt angle and the maximum load; c Tilt angle and yielding load; d L and yielding load).

Full size image

Discussion

To propose a potential method for the targeted preservation of wooden Tou-Kung joints, vertical strong compression tests were conducted to clarify the effects of Ang members on the load-carrying capacity and the introduction of the failure modes of different members. During the test, the Ang members were of three types: Xia-Ang, Wu-Ang and Shang-Ang. The horizontal length of the Ang members changed from 143 mm to 59 mm. In addition, the comparison of the wooden Tou-Kung joints of three different Ang structures was also detailed by the analysis of ke, Fu, Fmax, and D. Finally, the image acquisition system of the test system was employed to analyze the failure modes of the wooden Tou-Kung joints of different Ang structures. The following are obtained.

In general, the Ang member has a big influence on the load-carrying capacity. Compared to the other two constructions, the Xia-Ang structure is superior in terms of initial stiffness, ultimate load and maximum load capacity. The Shang-Ang structure demonstrates the best ductility, allowing it to absorb a considerable amount of energy even after the Tou-Kung joint reaches its ultimate load. As the load increases, both the vertical load and displacement of the Tou-Kung joint rise, with vertical stiffness initially increasing before it begins to decline.

The load-bearing capacity of wooden Tou-Kung joints depends on the types of Ang structures. This is inferred to be related to the title angle and length of the Ang structure. Based on the above discussion, the load-bearing capacity of the Xia-Ang Tou-Kung and Shang-Ang Tou-Kung would be different because of the Ang structures.

Through failure mode analysis of wooden Tou-Kung joints with different Ang configurations using digital image correlation(DIC), we conclude that the Tou-Kung joint exhibits four types of deformation. These include compression in the bucket-shaped structure, splitting of the Tou ears, and fractures in the middle of the Gong structure due to compression and bending deformation of the Ang structure. The extent of these deformations varies based on the length-to-thickness ratio of the Ang members. The main mode of damage in grain-oriented connections is wood cracking.

Based on the load-bearing capacity of wooden Tou-Kung joints, the focus on targeted preservation in historical buildings can be summarized in 2 aspects i.e., i) While the Ang structure primarily influences the mechanical properties of the Tou-Kung joints, the failure modes indicate that the Ludou and the Gong in contact with them are the most severely damaged components. ii) Both the horizontal length and the tilt angle of the Ang members affect the load-carrying capacity of the Tou-Kung joints. This correlation should be further verified through larger-scale tests, and the direction of the wood grain should also be considered in this context.