Introduction

The mural paintings at Dunhuang, located in the Mogao Caves, constitute a millennium-old Buddhist artistic treasure endowed with significant historical, aesthetic, and scientific value. However, the murals are currently exposed to multiple threats. Natural stressors such as desert aridity, wind erosion, and sand abrasion are compounded by anthropogenic influences, particularly the heat generated by visitors, which disrupts the caves’ microenvironment. These factors give rise to various forms of deterioration, including salt efflorescence, detachment voids, and flaking, which cause the pigment layers to peel, soften, and even detach, thereby posing a serious risk to the preservation of the murals. In response to multiple challenges, the Dunhuang Academy has established a systematic and scientifically grounded conservation framework for the murals. However, traditional restorative techniques remain detrimental to long-term preservation, often causing secondary damage and making intervention exceedingly difficult. Recent advances in image processing now provide a solid foundation for the digital restoration of the Dunhuang murals1.

Digital pictorial image restoration refers to the use of computational methods to reinstate damaged images. Specialized software and algorithms analyse, process, and reconstruct deteriorated or missing regions, recovering the original appearance of the artwork and providing essential support for cultural-heritage conservation and historical research2. Digital image inpainting methods can be broadly categorized into traditional methods and deep learning approaches. The core principle of traditional inpainting is to identify analogous pixel patches in the unmasked region and fill the missing area by copy and paste, as exemplified by algorithms based on partial differential equations3 and total variation4. These methods are effective for repairing small damaged regions, but their performance deteriorates when the image contains few similar areas or when the masked region is extensive.

Deep learning has achieved remarkable progress in image inpainting, primarily by learning visual features from large-scale datasets and progressively predicting the missing boundary information. Currently, two mainstream approaches are widely adopted: (i) encoder–decoder architectures based on convolutional neural networks (CNNs)5, and (ii) generative adversarial networks (GANs)6. Owing to their powerful representational capacity, these models can generate visually plausible completions. However, CNNs are limited in their ability to model global context due to the slow expansion of their receptive fields, hindering effective capture of long-range dependencies. To address this, Li et al.7 introduced a large selective-kernel mechanism that factorizes a large-kernel convolution into a series of depthwise convolutions and adaptively adjusts the receptive field through a spatial selection module, thereby improving contextual understanding. Cai et al.8 combined global average pooling with one-dimensional convolutions to successfully model long-distance pixel relationships and significantly enhance central-region features.

In the pursuit of superior inpainting quality, numerous researchers have proposed further refinements. Iizuka et al.9 developed an image completion method that employs both global and local context discriminators within an adversarial framework to ensure consistency across multiple scales; however, the method is unable to synthesize new textures or objects and focuses solely on local similarity without semantic comprehension of the scene. To address this limitation, Yang et al.10 jointly optimized image content and local texture by matching deep network patches with similar ones, thus preserving structural context while introducing high-frequency details, yet their approach struggles with high-resolution images, often resulting in blurry regions and imprecise boundaries, particularly in facial restoration tasks.

Zhang et al.11 proposed a domain-embedded GAN that incorporates facial structural and semantic priors into the generator, resulting in more natural and coherent facial reconstructions. A global discriminator enforces holistic spatial consistency, whereas a patch discriminator provides fine-grained facial details. However, the method still falls short in detail richness and sharpness. Tian et al.12 designed Pyramid-VAE-GAN, which seamlessly fuses the strengths of variational autoencoders (VAEs) and GANs: a VAE encodes high-level latent features to model complex priors, while a pyramid structure integrates multi-level latent representations to synthesize rich image details. Zeng et al.13 introduced AOT-GAN, leveraging Aggregated Contextual Transformations and an improved discriminator to significantly enhance inpainting quality. Nevertheless, the model requires re-optimizing AOT parameters for very large masks and tends to produce unrealistic boundaries for irregular masks.

Cao et al.14 further proposed PyramidFill, a fully convolutional GAN with a pyramid architecture. The content GAN, which employs gated and dilated-gated convolutions, generates low-resolution structural content, while the texture GAN utilizes a super-resolution and refinement network to synthesize high-resolution textures. Nonetheless, large missing regions can still result in structural misalignment and blurred boundary textures. To enhance fine-grained inpainting, Chen et al.15 introduced the Residual Feature-Attention Network (RFA-Net). Built on a non-pooling residual CNN and optimized with a hybrid loss module, RFA-Net drives the generator to focus on semantic and textural fidelity, thereby producing high-quality results. However, its reliance on pre-defined masks limits applicability in real-world scenarios where defect locations are unknown.

To address the absence of mask cues, Feng et al.16 devised a hierarchical contrastive learning framework that detects pixel-level damage masks by contrasting semantic differences between corrupted and intact regions, thereby enabling blind image inpainting. To better model global spatial structure, Dong et al.17 proposed an incremental Transformer-based method with mask position encoding, which upsamples low-resolution sketches using attention-based Transformers and accurately propagates structural features, demonstrating strong performance on large masks and complex scenes. Miao et al.18 introduced ITrans, combining CNNs and Transformers to leverage their complementary strengths in local detail extraction; however, limited capacity to model long-range semantic dependencies leads to blurred details and structural incoherence.

Li et al.19 developed a mask-aware Transformer model for large-mask completion, which dynamically updates valid tokens to capture long-range dependencies, producing diverse results while avoiding interference from invalid tokens. Shamsolmoali et al.20 proposed a context-adaptive Transformer that fuses encoder skip connections with coarse generator features, achieving improved global coherence and textural detail. Zhao et al.21 formulated an unsupervised cross-space translation GAN that establishes a one-to-one projection between instance-image space and conditional inpainting space, ensuring both appearance and structural consistency. Chen et al.22 introduced a multi-head, multi-tail pretrained Transformer backbone shared across diverse image-processing tasks, thereby improving relational understanding among patches. Zamir et al.23 presented an efficient Transformer for high-resolution image restoration that combines multi-scale local and global modeling without window partitioning, delivering pixel-level global context but exhibiting limitations in spatial-relation awareness for long-range dependencies.

Suvorov et al.24 proposed LaMa, which replaces standard convolutions with Fast Fourier Convolutions to capture global context with image-level receptive fields. LaMa handles large images effectively and, despite being trained on low-resolution data, performs effectively on high-resolution inputs. However, its intricate architecture complicates training and deployment. Liu et al.25 introduced VMamba, a vision backbone based on state-space models that extends the one-dimensional selective scan of the Mamba language model to two-dimensional data and employs four-directional scans to build long-range dependencies with linear complexity, yet conventional vision state-space models scan in a single fixed direction and lack two-dimensional spatial awareness. To address this limitation, Chen et al.26 proposed SEM-Net, a vision state-space-enhanced network that traverses pixels bidirectionally in snake-like order horizontally and vertically and augments positional awareness via a position-enhancement layer, thereby efficiently capturing both local and global pixel-level dependencies; nonetheless, insufficient emphasis on edge details results in low contrast, discontinuous structures, and blurred boundaries in the generated images.

To address the aforementioned issues, a Mural Restoration via Fusion of Edge-Guided and Multi-Scale Spatial Features (EGMF) is designed to boost restoration performance. The principal contributions are as follows:

  • This paper designs an Edge-Gauss Fusion Block (EGFB). This block combines an edge prior derived from the Scharr operator with an uncertainty-aware Gaussian modeling strategy. The direction-sensitive Scharr filters improve edge detection accuracy and reinforce edge details in low-quality image features. Simultaneously, the Gaussian modeling component estimates feature-wise variance to probabilistically refine low-confidence features, thereby amplifying salient structures while suppressing background noise.

  • We also propose a hybrid pyramid fusion mamba block (HPFMB). The block first employs dense spatial pyramid pooling (DSPP) to encode rich multi-scale semantic information through multiple pooling operations at different receptive field scales, producing fine-grained multi-scale feature representations. It then applies a pyramid fusion mamba (PFM) Module, whose selective scanning mechanism efficiently filters core semantic cues and removes redundant features. This not only enhances the representational capacity of the multi-scale features but also provides higher-quality feature foundations for subsequent layers.

Methods

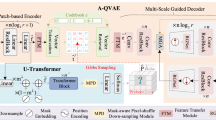
This paper proposes a mural restoration algorithm that integrates edge-guided features and multi-scale spatial features. The proposed model employs an encoder-decoder architecture based on the U-Net structure, and the overall network framework is shown in Fig. 1. Compared to SEM-Net, which relies solely on the spatial structure modeling (SSM)27 module for implicit spatial relationship modeling—leading to redundant multi-scale features and blurred edges—the proposed EGMF algorithm introduces the EGFB module to address these limitations. By incorporating the Scharr filter and Gaussian modeling28, EGFB explicitly enhances high-frequency edge details, effectively mitigating the structural discontinuity issues caused by SEM-Net’s implicit modeling. Furthermore, the HPFMB module, built upon the Mamba selective scanning mechanism29, dynamically filters redundant multi-scale semantic information. In contrast to SEM-Net, this design significantly improves the accuracy of texture reconstruction.

Fig. 1: Presents the architecture of the proposed image inpainting network, which is inspired by the framework introduced in ref. 26, with substantial modifications to the layout and design.
figure 1

The EGMF network adopts an encoder-decoder structure based on the U-Net. During the encoding stage, the Edge-Gaussian Cooperative Network (EGCN) is introduced to progressively extract multi-scale features. In the decoding stage, the PyramidMamba module is employed to capture richer multi-scale semantic information while reducing semantic redundancy during feature fusion.

Full size image

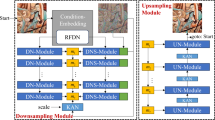
In the encoding stage, an EGCN, which is a multi-stage architecture capable of progressively extracting multi-scale features, is introduced. The downsampling rates from the first to the fourth stages are 1/4, 1/8, 1/16, and 1/32, respectively. This network primarily consists of Edge-Gaussian Fusion Blocks (EGFB) and the Deep Robust Feature Downsampling (DRFD) method. Specifically, the first stage of EGCN comprises N1 EGFB modules, which refine the input feature Fin at a downsampling rate of 1/4. Each EGFB integrates edge detection with Gaussian modeling, thereby enhancing robustness to noise as well as variations in object shape and orientation. In stages two through four, each stage begins with a DRFD module that combines convolution and max pooling for downsampling, effectively reducing spatial dimensions while preserving critical fine-scale features. Subsequently, stages two, three, and four contain N2, N3, and N4 EGFB blocks, respectively, for further refining features at downsampling rates of 1/8, 1/16, and 1/32. The EGFB blocks at each stage leverage either edge information or Gaussian modeling to enhance feature representation, making the network particularly suited for handling low-quality images.

In the decoding stage, the extracted spatial features are fed into the Spatially Enhanced Mamba (SEM) module to capture long-range dependencies and global structures. Additionally, an HPFMB block is introduced in intermediate layers of the decoder to extract richer multi-scale semantic information, aiding in the comprehensive interpretation of features at various scales within the image. Subsequently, the selective nature of the PFM module is utilized to effectively reduce homogeneous semantic information during multi-scale feature fusion. Ultimately, pixel-level modeling is applied to the damaged murals, completing the image restoration task.

Edge-Gaussian fusion block

To address artifacts and loss of edge details encountered in Dunhuang mural restoration, an Edge-Gaussian Fusion Block (EGFB) is proposed. This module enhances feature representations in low-quality images by integrating edge extraction and Gaussian modeling, thereby increasing the weighting of salient features, effectively improving image contrast, distinguishing foreground from background, and reinforcing edge textures, as illustrated in Fig. 1.

Initially, the input features Fin are passed through Edge-Gaussian Fusion Layers (EGFL) to generate an enhanced feature map. This feature map undergoes a 1 × 1 convolution layer, increasing the number of channels from C to 2C, followed by an AN layer to produce Fo1, as described in Eq. (1):

$${F}_{o1}=AN(Con{v}_{2D}^{1\times 1}(EGFB({F}_{in})))$$
(1)

Subsequently, Fo1 is processed through another 1 × 1 convolution, reducing the channels back to C. The convolution output is then normalized, and dropout is applied. Finally, the processed feature map is combined with the original input Fin to generate the output feature map Fo. This residual structure ensures that while effectively learning features from low-quality images, the integrity of the input features is preserved, as shown in Eq. (2):

$${F}_{o}={F}_{in}+Norm(drop(Con{v}_{2D}^{1\times 1}({F}_{o1})))$$
(2)

Considering the noise interference, low contrast, and blurred edge details common in the restoration of low-quality images, the EGFB block combines edge extraction with Gaussian modeling to enhance feature robustness. This approach enables the network to accurately capture edge details early on and subsequently focus on salient features, improving feature acquisition accuracy under complex conditions.

Edge extraction

In Stage 1, the feature resolution is reduced to one-quarter of the input size, while rich edge details and important high-frequency information are preserved. To extract reliable edge features from low-quality images, an improved Scharr filter is employed. This filter exhibits superior rotational invariance and minimizes edge response errors. The Scharr filter is defined as in Eq. (3):

$${S}_{x}=\left[\begin{array}{rcl}-3 & 0 & 3\\ -10 & 0 & 10\\ -3 & 0 & 3\end{array}\right],\,{S}_{y}=\left[\begin{array}{rcl}-3 & -10 & -3\\ 0 & 0 & 0\\ 3 & 10 & 3\end{array}\right]$$
(3)

The Scharr filters are assigned separately to the parameters of \({{\rm{Conv}}}_{2D}^{{S}_{x}}\) and \({{\rm{Conv}}}_{2D}^{{S}_{y}}\) convolutional layers, which process the input feature map Fin along the horizontal and vertical directions, respectively. The edge responses from both directions are then fused using the Euclidean norm to generate the final edge attention map Aedge, as expressed in Eq. (4):

$${A}_{edge}=\sqrt{{(Con{v}_{2D}^{{S}_{x}}({F}_{in}))}^{2}+{(Con{v}_{2D}^{{S}_{y}}({F}_{in}))}^{2}}$$
(4)

where Sx and Sy denote the convolutional filter parameters for the respective directions. This edge attention mechanism effectively enhances edge information before further processing.

Gaussian modeling

From Stage 2–4, as the feature dimensions continue to decrease, the model’s ability to discriminate edge information gradually diminishes. However, the features of the input image tend to approximate a Gaussian distribution centered around a specific point. To better capture relevant features, Gaussian convolution kernels are employed to retain both critical and uncertain features, and to mitigate feature degradation during forward propagation.

To enhance salient features, a fixed Gaussian kernel is used. The Gaussian filter assigns weights to pixels based on the distance from the kernel center, with closer pixels receiving larger weights. This weighting suppresses background noise while accentuating prominent structures in the image. Owing to this property, the Gaussian filter excels at highlighting discriminative regions within the feature map, allowing the network to focus on informative content and minimizing artifacts introduced by high-frequency noise. The Gaussian kernel is defined in Eq. (5):

$${G}_{\sigma }^{k\times k}({\rm{x}})=\frac{1}{2\pi {\sigma }^{2}}{e}^{-\frac{{x}^{2}+{{\rm{y}}}^{2}}{2{\sigma }^{2}}}$$
(5)

where k×k denotes the kernel size, and σ is the standard deviation, which is set to 1.0 for optimal edge detection performance.

The Gaussian kernel is applied via depth-wise convolution to independently smooth each channel. Gaussian modeling, denoted as Agauss, is computed as shown in Eq. (6):

$${A}_{gauss}={G}_{1.0}^{5\times 5}({F}_{in})$$
(6)

Edge-Gaussian fusion layers

As shown in Fig. 2, the input feature Fin is first processed through an Edge-Gaussian Collaborator (EGC) module to generate the feature Fegc. To emphasize critical channels, an efficient channel attention (ECA) module is incorporated. The ECA module reduces dimensions and facilitates appropriate cross-channel interaction, effectively lowering model complexity while maintaining performance. The EGC operations are described in Eqs. (7 and 8):

$${F}_{o1}=Sigmoid(Con{v}_{1D}^{k}(GAP({F}_{egc})))$$
(7)
$${F}_{o}=Norm(({F}_{o1}\otimes {F}_{egc})+{F}_{in})$$
(8)

where, \(Con{v}_{1D}^{k}\) represents an adaptive one-dimensional convolution, where the kernel size k is proportional to the number of channels C, and GAP denotes global average pooling along the channel dimension. This strategy selectively enhances critical channels while minimizing redundant features, thereby improving the semantic richness of the representations.

Fig. 2: Illustrates the architecture of the EGFL network. Influenced by the design in ref. 36, this structure has been adapted to improve edge detection accuracy.
figure 2

The EGFL network first applies an enhanced Scharr filter to extract reliable edge features and generate an attention map. A Gaussian filter is then used to emphasize salient image features while suppressing background noise.

Full size image

Since edge information is most effectively utilized in shallow network layers, incorporating it into deeper layers may not improve performance and can even hinder the network’s ability to learn complex, high-order features. This typically leads to suboptimal convergence or training difficulties. Therefore, for deeper features, Gaussian modeling is adopted. By representing feature distributions as Gaussian, noise interference is effectively reduced.

To balance the contributions of the original input image and its corresponding edge features, a residual connection is incorporated into the EGFB module. This facilitates network adaptability and dynamic adjustment, enabling effective mitigation of potential adverse effects.

In summary, the EGFB module enhances the robustness of low-quality feature representations by combining edge extraction and Gaussian modeling, enabling precise capture of edge features and textural details in degraded images.

EGC module

As illustrated in Fig. 3, the EGC module processes the input feature Fin through a selection mechanism. Depending on the stage, either edge extraction or Gaussian modeling is applied, as defined in Eq. (9):

$${A}_{eg{\rm{a}}}=\left\{\begin{array}{l}{A}_{edge}({F}_{in}),if\,Stage=1,\\ {A}_{gauss}({F}_{in}),otherwise\end{array}\right.$$
(9)
Fig. 3
figure 3

Shows the structure of the EGC module, which enhances the robustness of low-quality features by integrating edge extraction with Gaussian modeling, thereby enabling precise capture of edge features and fine textures in degraded images.

Full size image

The result Aega is added element-wise to Fin, and the sum is processed through a convolutional block (Conv_Block) to enhance the feature representation, producing the output Fa, as shown in Eq. (10):

$${F}_{a}=Conv\_Block({F}_{in}\oplus {A}_{eg{\rm{a}}})$$
(10)

where⊕denotes element-wise addition. The Conv_Block is a sequential processing unit defined as follows: a 1 × 1 convolution to adjust channel dimensions, an activation-normalization layer, a 3 × 3 convolution to capture spatial relationships, another AN layer, a final 1 × 1 convolution to restore the original number of channels, and a concluding normalization layer. Specifically, for input X, Conv_Block(X) is defined in Eq. (11):

$$\left\{\begin{array}{l}{X}_{1}=Con{v}_{2D}^{1\times 1}(X)\\ {X}_{2}=AN({X}_{1})\\ {X}_{3}=Con{v}_{2D}^{3\times 3}({X}_{2})\\ {X}_{4}=AN({X}_{3})\\ {X}_{5}=Con{v}_{2D}^{1\times 1}({X}_{4})\\ Conv\_Block(X)=Norm({X}_{5})\end{array}\right.$$
(11)

where X = Fin⊕Aega, and the 1 × 1 convolution adjusts channel size as needed.

Further refinement is achieved by combining Fin and Fa using element-wise multiplication and addition operations, followed by a 3 × 3 convolution to produce the final feature Fegc, as defined in Eq. (12):

$${F}_{egc}=Con{v}_{2D}^{3\times 3}(({F}_{in}\otimes {F}_{a})+{F}_{in})$$
(12)

where, \(\otimes\) denotes element-wise multiplication.

HPFMB

To strengthen the model’s ability to represent multi-scale features, an HPFMB Block is introduced. First, DSPP is applied to capture multi-scale semantic features, thereby producing finer-grained contextual information. Next, a selectively adaptive Mamba module employs its filtering mechanism to reduce semantic redundancy within the multi-scale feature maps. Finally, a Convolutional Feedforward Network (ConvFFN) is incorporated to further enhance the representational capacity of these multi-scale features.

DSPP

To obtain multi-scale semantic features, DSPP is proposed, as illustrated in Fig. 4, where rich semantic information is encoded through pooling operations at multiple scales.

Fig. 4: Depicts the DSPP network architecture. Initially inspired by ref. 37, this design has undergone subsequent modifications.
figure 4

The DSPP network utilizes multiple average pooling operations at different scales to generate feature maps, which are then upsampled via bilinear interpolation to match the original resolution and concatenated along the channel dimension to form a multi-scale feature representation.

Full size image

Specifically, the high-level feature map extracted by the encoder is first processed by the SEM module to capture long-range dependencies and global structure. The resulting output is then fed into the DSPP module, where C and N represent the channel dimension and spatial resolution of the input feature map, respectively. DSPP performs average pooling at multiple scales to generate a set of multi-scale feature maps, upsamples each by bilinear interpolation to match the original resolution, and concatenates them along the channel dimension to form a comprehensive multi-scale feature map, as shown in Eq. (13).

$${P}_{i}=ConvPoo{l}_{i}(X),\,i\in {A}_{step}^{(1,M)}$$
(13)

where ConvPooli denotes an average-pooling operation with pooling scale i, followed by a standard convolution with a 1 × 1 kernel, and \({P}_{i}\in {{\mathbb{R}}}^{c\times i\times i}\) is the resulting pooled feature map. The pooling scale \(i\) is taken from an arithmetic sequence \({A}_{step}^{(1,{\rm{M}})}\) whose maximum value is M = N-1 and whose common difference is \(step=\frac{{\rm{N}}}{8}\).

Subsequently, the pooled feature maps are upsampled via bilinear interpolation, so that their spatial resolution matches that of the higher-level feature maps, as shown in Eq. (14).

$${U}_{i}=BilinearUp({P}_{i})$$
(14)

where \({U}_{i}\in {{\mathbb{R}}}^{C\times N\times N}\) concatenates the upsampled feature maps along the channel dimension to generate a multi-scale feature map, as expressed in Eq. (15).

$${X}_{ms}=Concat(X,{U}_{1},\mathrm{..}.,{U}_{M})$$
(15)

where \({X}_{ms}\in {{\rm{{\mathbb{R}}}}}^{[(\frac{M-1}{2}+1)c+C]\times N\times N}\). However, applying bilinear interpolation to pooled features that originate from the same feature map introduces a substantial amount of semantically homogeneous information, thereby causing redundancy in the resulting multi-scale feature representations.

PFM

To mitigate information redundancy during multi-scale feature fusion, we proposed the PFB, as illustrated in Fig. 5. HPFMB leverages the Mamba selective filtering mechanism to distill core semantic information from multi-scale features, thereby markedly reducing redundancy and enhancing the overall multi-scale visual representation. By virtue of its built-in selective filtering capability, the module effectively captures salient semantics across scales.

Fig. 5: presents the Mamba network architecture.
figure 5

The Mamba module employs a selective filtering mechanism to suppress redundant information and enhance multi-scale visual representations.

Full size image

Initially, the multi-scale features undergo dimensionality reduction: a flatten operation is applied to generate a pyramid sequence, as defined in Eq. (16).

$${X}_{flat}=Flatten({X}_{ms})$$
(16)

where \({X}_{flat}\in {{\rm{{\mathbb{R}}}}}^{{N}^{2}\times [(\frac{M-1}{2}+1)c+C]}\) denotes the pyramid sequence, which is subsequently forwarded to the Mamba module for selective feature extraction, as formalized in Eq. (17).

$${X}_{select}=Mamba({X}_{flat})$$
(17)

The selectively extracted multi-scale features Xselect are subsequently fed into a Convolutional FeedForward Network to enhance their representational power. The ConvFFN comprises a series of convolutional layers followed by normalization, nonlinear activation, and dropout operations, as formalized in Eq. (18).

$${X}_{conv}=ConvBNReLU({X}_{select})$$
(18)

where ConvBNReLU denotes a one-dimensional convolution layer with a kernel size of 1, followed in sequence by batch normalization and a ReLU activation. Subsequently, two fully connected 1D convolution layers are applied, each equipped with a GELU activation and a dropout operation for regularization, as detailed in Eqs. (19–23).

$${X}_{fc1}=Conv({X}_{conv})$$
(19)
$${X}_{act}=GELU({X}_{fc1})$$
(20)
$${X}_{drop}=Dropout({X}_{conv})$$
(21)
$${X}_{fc2}=Conv({X}_{drop})$$
(22)
$${X}_{out}=Dropout({X}_{fc2})$$
(23)

Through the Mamba-based HPFMB, the model effectively aggregates multi-scale features and suppresses homogeneous information, thereby achieving precise image reconstruction.

Results

Dataset settings

To assess the effectiveness of the proposed image restoration method, we carry out comparative experiments on the Dunhuang Mural dataset. This study employs the Dunhuang Mural Challenge Dataset supplied by the Dunhuang Academy30. The dataset comprises 2850 mural images at a resolution of 256 × 256 pixels, partitioned into 2700 training images, 50 validation images, and 100 test images. It spans diverse subjects such as Flying Apsaras, Arhats, temples, and costumes.

To comprehensively evaluate the restoration performance under varying degrees of degradation, the masked images are categorized into five distinct classes based on the proportion of the damaged area: 1–10%, 10–20%, 20–30%, and 30–40%, and a dedicated powder-like mask category simulating granular surface degradation. The masks are generated with randomized sizes, shapes, and spatial distributions across the image, covering mask ratios from 1% to 40% to emulate a spectrum of lesion extents and morphological diversity. The mask area directly correlates with the severity of corruption; within each class, diverse masking strategies are applied to construct the training set, ensuring the model is exposed to a wide range of defect patterns. Furthermore, to validate the practical effectiveness and generalization of the algorithm, 19 authentic damaged Dunhuang mural images featuring real-world deterioration patterns are incorporated into the evaluation.

Experimental platform and evaluation indicators

Experimental Setup: The experiments were run on identical workstations equipped with a 12th Gen Intel® CoreTMi7-12700KF*20, running Ubuntu 18.04.6 LTS. The graphics processing unit (GPU) used is an NVIDIA GeForce RTX 4080 Ti (PCIe/SSE2). The codebase is implemented in Python 3.8, and training is carried out with the PyTorch deep-learning framework. For optimization during training, the Adam optimizer was utilized. The initial learning rate was set to 1 × 10-4, and the learning rate ratio between the discriminator and generator is set to 0.1. This methodology guarantees robust convergence and maximizes performance throughout the entirety of the training procedure.

Simulated inpainting of damaged murals: experiment and analysis

To validate the effectiveness of the EGMF algorithm, experiments were conducted to simulate varying degrees of mural damage. During the training phase, the training set was augmented with random masks and powder-like masks ranging from 1% to 40% coverage to train the restoration model. To facilitate a comparative analysis with the proposed mural restoration method, we selected six state-of-the-art approaches: LEGNet31, DSNet32, T-former33, HINT34, PUT12, and SEM26. In the testing phase, damaged mural images and their corresponding masks were jointly input into the model for restoration. Five representative restoration results were randomly selected from the test outcomes for qualitative visualization and analysis.

Quantitative analysis

To ensure a comprehensive and objective evaluation of each algorithm on the restoration task, the experiment employed four metrics: peak signal-to-noise ratio (PSNR), structural similarity (SSIM), perceptual similarity (LPIPS), mean L1 norm error, and perception-based image quality evaluator (PIQE). Higher PSNR and SSIM values correspond to better restoration performance, whereas lower L1 and LPIPS values indicate superior results. All the values reported in Table 1 represent the average performance across 100 test images for each mask type (1–40%). Figure 6 presents only five representative visualized results for qualitative comparison. The detailed quantitative results are shown in Table 1.

Fig. 6: Compares the inpainting results of various algorithms under different occlusion rates.
figure 6

a Original image, b Mural with artificial occlusions (occlusion patterns adapted from refs. 30,38, licensed under CC BY 4.0), c LGNet31, d DSNet32, e T-former33, f HINT34, g PUT12, h SEM26, and i the proposed method.

Full size image
Table 1 Quantitative comparison of various repair algorithms under different mask rates
Full size table

As shown in Table 1, the EGMF algorithm demonstrates consistently outstanding restoration performance across varying mask rates. At mask rates between 1% and 20%, all evaluation metrics for EGMF outperform those of the comparison methods, primarily attributable to its superior ability to preserve edge details and structural information. When the mask rate increases to between 20% and 40%, EGMF still maintains its performance advantage, with PSNR and SSIM values remaining higher than those of the other algorithms. This indicates that the EGMF algorithm is capable of effectively preserving both the structural and spatial information of the murals even under high mask rates. This ability to maintain structural integrity under severe occlusion enables the EGMF algorithm to achieve high-quality restoration results.

Qualitative analysis

Figure 6 presents the visualized restoration results for five randomly selected Dunhuang murals under varying mask coverage rates. Specifically, Fig. 6a shows the original murals, Fig. 6b displays the murals with applied masks, and Fig. 6c–i illustrate the restoration outputs of LEGNet, DSNet, T-former, HINT, PUT, SEM, and the complete EGMF algorithm, respectively. The blue bounding boxes highlight the damaged regions, enabling a clear comparison of each algorithm’s restoration performance in those areas.

In the 1–10% mask regime, LEGNet’s three-stage strategy expands the receptive field to capture global context but inadequately models intricate mural textures, resulting in blurred facial contours. HINT’s hierarchical multi-head attention preserves some local details; however, as shown in Fig. 6c, it fails to maintain continuity in background line structures, indicating structural information loss. DSNet employs dilated convolutional blocks to aggregate multi-scale semantic features, yet its limited detail retention yields blurred local textures. T-former’s novel attention mechanism reduces computational complexity while modeling long-range dependencies; nevertheless, approximation errors during complex texture handling still produce fuzzy details. PUT, built on a Transformer architecture, leverages global context to recover texture and structure but occasionally introduces local discontinuities. By contrast, SEM’s spatially enhanced self-similarity module (SSM) efficiently models pixel-level dependencies and preserves structural consistency, and EGMF’s edge-Gaussian collaborative network architecture further refines both structural and textural restoration. In Fig. 6i, EGMF accurately reconstructs the head and hand regions, yielding results that are visually consistent with the originals.

For 10–20% masking, LEGNet, DSNet, T-former, and HINT each fail to fully reconstruct facial structure, leading to contour loss and structural breaks. PUT and SEM maintain overall structural and textural coherence, but still exhibit facial distortion and blurred edges. EGMF, however, uses a multi-scale feature pyramid network to enhance feature correlation and capture richer context, thereby restoring edge details more accurately and producing sharper, more detailed results.

When masks cover 20–30% of the area, LEGNet, T-former, and HINT show feature omissions and misaligned structures: large portions of background and Buddha contours lack detailed textures, preventing effective reconstruction. Although SEM and PUT capture global context, they introduce artifacts and structural discontinuities when reconstructing apparel regions. EGMF, in contrast, preserves global structure and retains critical local details within damaged areas, yielding more natural and coherent restorations. It is worth noting that while our method achieves the best performance in the majority of metrics, the LPIPS value for the 20–30% mask range is slightly higher than that of HINT. We attribute this minor discrepancy to the fact that HINT’s hierarchical attention mechanism might occasionally yield marginally better perceptual similarity for specific texture patterns under moderate occlusion. However, our approach consistently outperforms HINT across all other quantitative metrics (PSNR, SSIM, L1, and PIQE) and, more importantly, delivers superior visual coherence and structural accuracy as demonstrated in the qualitative analysis, which are critical for mural restoration. This ability to maintain structural integrity under severe occlusion enables the EGMF algorithm to achieve high-quality restoration results.

Under 30–40% masking, T-former blurs the stamen region, losing both structural information and key features. LEGNet, DSNet, and HINT produce varying degrees of blurring and spatial discontinuities in annotated areas. PUT and SEM capture short- and long-range dependencies but still suffer from artifacts and blurred textures. In comparison, EGMF consistently preserves edge features and global spatial coherence, resulting in visually natural and coherent restorations. Although the LPIPS value for the 30–40% mask range is very close to that of SEM-Net and slightly higher than HINT’s, the comprehensive superiority across PSNR, SSIM, and L1 error demonstrates the overall effectiveness of our approach in balancing pixel-level accuracy, structural fidelity, and perceptual quality.

In tests with powder-like masks, LEGNet, DSNet, and PUT fail to preserve edge details and structural information around key regions. T-former and HINT refine local edge details but lose some facial features. SEM and EGMF both enhance edge features and spatial positions without loss; they excel in detail reproduction and global structural coherence, maintaining the overall style and fine details of the murals.

Overall, EGMF outperforms all compared methods in visual quality and quantitative metrics, effectively restoring complex mural content across all mask types and coverage rates.

Difference map analysis

To quantitatively assess the restoration accuracy of EGMF, we conducted a comparative experiment under 10–20% mask coverage. Figure 7 presents the difference map obtained by computing the mean L1 error between the restored mural image and the corresponding ground-truth mural. Figure 7a illustrates an original mural depicting a monk in worship, and Fig. 7b shows the murals with applied masks. Figures 7c–p present the difference maps for LEGNet, DSNet, T-former, HINT, PUT, SEM, and the proposed EGMF method, respectively. EGMF’s mean L1 error is 0.0034 lower than that of the baseline algorithms, demonstrating superior semantic consistency and robustness.

Fig. 7: Shows the residual difference maps of inpainting results by various algorithms.
figure 7

a Input, b Original image, c LGNet, d Difference plot, e DSNet, f Difference plot, g T-former, h Difference plot, i HINT, j Difference plot, k PUT, l Difference plot, m SEM, n Difference plot, o the proposed method, p Difference plot. The quality of restoration is evaluated by zooming into selected regions and conducting a quantitative analysis using the L1 loss metric.

Full size image

The restoration difference maps were generated by performing pixel-wise subtraction between the inpainted and original mural images. Visually, the proposed algorithm’s difference maps exhibit markedly smaller highlighted discrepancies and lower L1 loss values compared to the other methods. This superior fidelity and consistency further validate the proposed algorithm’s effectiveness and robustness in the mural restoration task.

Ethical declaration

All mural images employed in this study originate from publicly accessible cultural heritage databases. As the images represent historical artworks without involving any identifiable individuals, this study does not require ethical approval or written informed consent. In addition, the FFHQ facial image datasets utilized in this study were sourced from publicly accessible repositories.

Ablation experiment and universality analysis

Module ablation experiment

For mural mask coverages between 10% and 20%, the contribution of each proposed module to restoration performance was evaluated by incorporating the module into the baseline model sequentially, followed by retraining and testing. Employing a univariate analysis, the EGFB and HPFMB modules were integrated into the model in succession, and the experimental results were assessed from both quantitative and qualitative perspectives.

Quantitative Analysis: The comparison of quantitative results of module ablation experiments are summarized in Table 2. The first row reports the evaluation metrics of the baseline model without any added modules; the second row corresponds to the baseline model augmented with the EGFB module; the third row corresponds to the baseline model augmented with the HPFMB module; and the fourth row corresponds to the EGMF algorithm model, which integrates all modules. The inclusion of different modules produces significant changes in the performance metrics. After adding the EGFB module, PSNR increases by 0.013, SSIM increases by 0.0064, L1 loss decreases by 0.0011, and LPIPS decreases by 0.004. After adding the HPFMB module, PSNR increases by 0.079, SSIM increases by 0.0066, L1 loss decreases by 0.0017, and LPIPS decreases by 0.008. When the EGMF algorithm combines all modules, PSNR increases by 0.192, SSIM increases by 0.007, L1 loss decreases by 0.002, and LPIPS decreases by 0.011. After integrating all modules, the model exhibits increases in the number of parameters, floating-point operations (GFLOPs), and inference time compared with the baseline model SEM.

Table 2 Comparison of quantitative results of module ablation experiments
Full size table

These results demonstrate that all evaluation metrics improve as modules are progressively introduced. With each additional module, the model’s performance steadily climbs; when all modules operate in concert, the model attains its optimal image restoration capability.

Qualitative Analysis: Fig. 8 presents the visualized restoration results obtained by sequentially integrating each module into the model. To clarify each module’s contribution, blue boxes highlight regions where restoration differences are evident. Specifically, Fig. 8a presents the original murals, Fig. 8b shows the murals with applied masks, Fig. 8c displays the restoration result from the baseline SEM model, Fig. 8d shows the output after incorporating the EGFB module, Fig. 8e shows the output after adding the HPFMB module, and Fig. 8f shows the restoration produced by the proposed EGMF algorithm, which combines all modules.

Fig. 8: Illustrates the results of the ablation study.
figure 8

a Original image, b mural with artificial occlusions (occlusion patterns adapted from refs. 30,38, CC BY 4.0), c SEM, d SEM + EGFB, e SEM + HPFMB, and f the proposed method.

Full size image

The baseline SEM model exhibits structural distortions and a loss of edge detail when reconstructing extensively damaged regions. For instance, in the first row of Fig. 8c, the traveling monk’s shoulder region displays slight blurring artifacts. In the third row of Fig. 8c, the Bodhisattva’s praying-hands region suffers from texture-detail loss and minor fuzziness. After introducing the EGFB module, restoration performance improves significantly compared to the baseline; spurious artifacts present in the masked mural are suppressed, and blurring is reduced, as evidenced in the first and third rows of Fig. 8d. Nevertheless, in the third row of Fig. 8e, the palm region continues to show structural misalignment and blurred edge contours. Upon integrating the HPFMB module, its DSPP mechanism captures finer-grained multi-scale context and enhances feature representation across scales. For example, the ornamental region in the second row of Fig. 8e and the background annotation area in the fourth row of Fig. 8e are restored with increased realism. Ultimately, the EGMF algorithm that fuses both the EGFB and HPFMB modules achieves restoration quality that closely approximates the ground-truth mural in terms of overall structural continuity and preservation of edge-detail textures, particularly in regions characterized by intricate edges and complex textures, as shown in Fig. 8f.

Universal experiment

To demonstrate the generalizability of the EGMF algorithm, experiments were conducted on the FFHQ dataset35. Figure 9a presents the original ground-truth images, Fig. 9b shows the masked images, Fig. 9c illustrates the restoration results of the baseline model SEM, Fig. 9d displays the results after incorporating the EGFB module, Fig. 9e shows the outcomes with the HPFMB module added, and Fig. 9f depicts the final results with all modules integrated. The quantitative results are detailed in Table 3.

Fig. 9: Demonstrates the results of the generalization experiments.
figure 9

a Original image, b Input, c SEM, d SEM + EGFB, e SEM + HPFMB, and f the proposed method. Displays the generalization performance of the proposed algorithm through ablation experiments conducted on the FFHQ dataset35, demonstrating strong adaptability across various scenarios.

Full size image
Table 3 Comparison of quantitative results of module universal experiments
Full size table

As shown in Table 3, all proposed modules contribute to consistent performance improvements on the FFHQ dataset. The complete EGMF algorithm achieves the best values across all evaluation metrics: a PSNR of 28.7954, an SSIM of 0.9104, an L1 loss of 0.0088, and an LPIPS of 0.0678. These quantitative results further validate the effectiveness and generalizability of EGMF on natural images.

As shown in Fig. 9, the baseline model exhibits issues such as blurry facial texture details, structural inconsistencies, and noticeable inpainting artifacts. For instance, the forehead in the first and third rows of Fig. 9c, the pearl accessory in the second row, and the hair direction and shape in the fourth row. With the introduction of the EGFB module, the restoration process benefits from enhanced structural guidance based on edge features, significantly improving the visual coherence of the restored images. However, some edge structure loss remains, as evidenced by missing details and inconsistent hair patterns in the fourth row of Fig. 9d.

With the further introduction of the HPFMB module, pyramid feature fusion enables the capture of finer-grained multi-scale contextual information and reduces semantic redundancy within multi-scale features, thereby significantly improving multi-scale feature representation. For instance, the mouth texture in the third row of Fig. 9e is more consistent with the original image, and the structure of the hair region appears more coherent. When all modules are integrated, the model demonstrates superior performance in reconstructing complex textures and structures, effectively preserving the original characteristics and details of the murals. For example, the restoration of the mouth and forehead regions in the third row of Fig. 9f retains a significant amount of detail and structural information, resulting in a more natural and realistic visual appearance.

In summary, the EGMF algorithm demonstrates broad application potential across diverse scenarios. Based on extensive testing and comparative analysis on the FFHQ dataset, the EGMF algorithm effectively handles various types of image degradation, showing superior performance in both texture detail recovery and overall structural coherence.

Real damaged mural inpainting experiment

To further validate the restoration performance of the EGMF algorithm on genuinely damaged mural images, four real-world damaged murals were randomly selected, and their damaged regions were masked and inpainted. In each case, Fig. 10a depicts the original murals, Fig. 10b shows the murals after mask application, and Fig. 10c–i present the restoration results obtained by LEGNet, DSNet, T-former, HINT, PUT, SEM, and the proposed EGMF algorithm, respectively. For each method, discrepancies within the true damaged regions are highlighted with blue bounding boxes; the corresponding visual results are shown in Fig. 10.

Fig. 10: Provides a comparison of real-world mural restoration results across different algorithms.
figure 10

a Original image, b mural with artificial occlusions (occlusion patterns adapted from refs. 30,38, CC BY 4.0), c LGNet, d DSNet, e T-former, f HINT, g PUT, h SEM, and i the proposed method.

Full size image

In the first mural, none of the comparative algorithms fully reconstructs the original line structures. The T-former output exhibits large areas of blurring, while LEGNet and DSNet produce relatively clear restorations but still suffer from missing local details. HINT and PUT both introduce structural misalignments, whereas SEM and EGMF achieve noticeably better results, generating sharper textures and coherent structures. For example, see the first row of Fig. 10i. In the second mural, LEGNet and PUT again manifest structural inconsistency and feature loss, while the EGMF restoration retains texture details and preserves structural continuity. In the third mural, all comparative methods yield blurred structures and broken line segments; by contrast, EGMF delivers a more precise and detailed reconstruction of critical features. In the fourth mural, LEGNet produces extensive artifacts, whereas all other methods, including EGMF, successfully achieve high-quality restorations.

Overall, the EGMF algorithm demonstrates significant advantages when applied to real damaged murals. Its restoration outputs not only preserve mural edge features and global spatial arrangements more effectively than competing approaches, but also achieve superior continuity and natural transitions in the overall structure. Visually and perceptually, the EGMF results appear more vivid and realistic.

Discussion

This paper presents a novel mural restoration model that integrates edge-guided features with multi-scale spatial features. The proposed framework incorporates two key components: the Edge-Gaussian Fusion Block and the HPFMB. The EGFB lock enhances high-frequency edge details in low-quality image features, thereby improving the extraction of texture information in murals. Concurrently, the HPFMB block captures fine-grained multi-scale contextual information through hierarchical feature fusion, significantly enhancing multi-scale visual representations and mitigating semantic redundancy. Collectively, these enhancements effectively address common challenges in mural restoration, such as the presence of visual artifacts and distortion of edge details.

Experimental results demonstrate that the proposed EGMF algorithm achieves superior performance in mural restoration tasks, consistently outperforming existing methods across both objective and subjective evaluation metrics. On the FFHQ dataset, the algorithm delivers satisfactory results, validating its generalizability. Ablation studies on the Dunhuang mural dataset show that the EGMF algorithm yields a relative improvement in PSNR of 0.013–0.192, a relative increase in SSIM of 0.006–0.007, a relative reduction in L1 loss of 0.001–0.002, and a relative decrease in LPIPS of 0.004–0.011 compared to the baseline model. These findings indicate that the EGMF algorithm not only preserves critical edge textures and provides precise reconstruction guidance, but also effectively recovers complex textures and structural details in mural images.

In conclusion, the EGMF algorithm demonstrates robust and comprehensive capabilities for mural restoration. It successfully maintains global structural and textural coherence while accurately reconstructing fine-grained edge details and intricate patterns. The superior PSNR and SSIM values, in comparison with other state-of-the-art methods, highlight its advantage in delivering high-quality restoration outcomes.

Despite the promising performance achieved by the EGMF algorithm, this study has certain limitations. The performance advantage of our method, particularly in perceptual metrics like LPIPS, diminishes when handling extremely large mask regions or highly complex structural degradations such as widespread cracking and flaking. This can be attributed to the increased ambiguity and the lack of sufficient contextual priors for the model to reliably infer the missing content. Furthermore, the current model is primarily trained and optimized on the Dunhuang mural dataset, which may limit its effectiveness when directly applied to murals with distinctly different artistic styles or degradation patterns from other cultural backgrounds. The incorporation of multi-scale feature fusion and Mamba modules, while improving performance, also introduces additional computational overhead compared to simpler architectures, which could be a consideration for resource-constrained deployment scenarios. Future work will focus on enhancing the model’s robustness to extreme damage conditions and its generalization across a more diverse spectrum of cultural heritage artifacts.