Abstract
Background
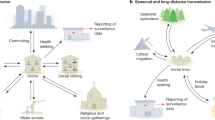
Predicting infection outbreak dynamics within local microenvironments is a challenging task. Some methods assume smaller population pools and often lack the statistical power of inferences. Other methods are designed for larger population pools and cannot be downscaled to accommodate the details of microenvironments, such as a gym or cafeteria. Moreover, typically, individuals have a relatively small circle of friends, family, and co-workers with whom most contacts are taking place, while the external contacts occur sporadically, rendering the population clustered. Practicable infection risk assessment models should account for population size, geometry and occupancy of public places, behavioral and professional patterns that define daily routines, and societal structure.
Objective
We describe a novel methodology and investigate effects of the population social structure, along with other local constraints, on infection outbreak dynamics.
Methods
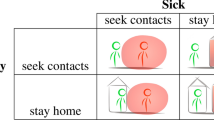
The study is based on the recently developed stochastic microexposure model (S-MEM). The model has been generalized to describe clustered populations. The methodology is demonstrated for a generic community of several thousand students living on campus. The student population possesses a natural social structure of being clustered into classes.
Results
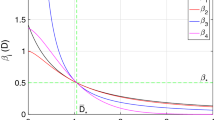
The results indicate that the social structure has the first order effect on the spread of the infection. Depending on the number, size, and degree of inner- and outer-cluster connections, the outbreak exhibits distinct durations, power, and multiple peaks of infection. Moreover, the contribution of different microenvironments to infection risk evolves during the course of the outbreak.
Impact
-
Social structure plays a major role in infection spread, and therefore should be accounted for in risk prediction tools. Furthermore, the contribution of different microenvironments to infection risk changes with time during the course of an outbreak. An optimal infection spread mitigation policy should, correspondingly, change in time depending on the evolving risk factors; the policy should not be static. The stochastic microexposure model accounts for the social structure of a population at multiple scales, and can predict the dynamic contributions of different microenvironments to infection spread risks.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 6 print issues and online access
$259.00 per year
only $43.17 per issue
Buy this article
- Purchase on SpringerLink
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout






Similar content being viewed by others
Data availability
Detailed information on model parameters and calibration can be found in ref. [25].
References
Kermack WO, McKendrick AG. A contribution to the mathematical theory of epidemics. Proc R Soc Lond Ser A, Containing Pap A Math Phys character. 1927;115:700–21.
Kermack WO, McKendrick AG. Contributions to the mathematical theory of epidemics—II. The problem of endemicity. Bull Math Biol. 1991;53:57–87.
Kermack WO, McKendrick AG. Contributions to the mathematical theory of epidemics—III. Further studies of the problem of endemicity. Bull Math Biol. 1991;53:89–118.
He S, Peng Y, Sun K. SEIR modeling of the COVID-19 and its dynamics. Nonlinear Dyn. 2020;101:1667–80.
Weissman GE, Crane-Droesch A, Chivers C, Luong T, Hanish A, Levy MZ, et al. Locally informed simulation to predict hospital capacity needs during the COVID-19 pandemic. Ann Intern Med. 2020;173:21–8.
Calvetti D, Hoover A, Rose J, Somersalo E Bayesian dynamical estimation of the parameters of an SE (A) IR COVID-19 spread model. arXiv preprint arXiv:200504365. 2020.
Clancy D, O’Neill PD. Bayesian estimation of the basic reproduction number in stochastic epidemic models. Bayesian Anal. 2008;3:737–57.
Chen Y-C, Lu P-E, Chang C-S, Liu A. Time-Dependent SIR Model for COVID-19 With Undetectable Infected Persons. In IEEE Transactions on Network Science and Engineering. 2020;7:3279–94.
Newman ME. Spread of epidemic disease on networks. Phys Rev E. 2002;66:016128.
Ma J, van den Driessche P, Willeboordse FH. Effective degree household network disease model. J Math Biol. 2013;66:75–94.
Rǎdulescu A, Williams C, Cavanagh K. Management strategies in a SEIR-type model of COVID 19 community spread. Sci Rep. 2020;10:21256.
Salathé M, Jones JH. Dynamics and Control of Diseases in Networks with Community Structure. PLOS Comput Biol. 2010;6:e1000736.
Tolles J, Luong T. Modeling epidemics with compartmental models. Jama. 2020;323:2515–6.
Cuevas E. An agent-based model to evaluate the COVID-19 transmission risks in facilities. Comput Biol Med. 2020;121:103827.
Silva PCL, Batista PVC, Lima HS, Alves MA, Guimarães FG, Silva RCP. COVID-ABS: An agent-based model of COVID-19 epidemic to simulate health and economic effects of social distancing interventions. Chaos Solitons Fractals. 2020;139:110088.
Shamil MS, Farheen F, Ibtehaz N, Khan IM, Rahman MS. An agent-based modeling of COVID-19: validation, analysis, and recommendations. Cognitive Comput. 2024:16:1723–34.
Kerr CC, Stuart RM, Mistry D, Abeysuriya RG, Rosenfeld K, Hart GR, et al. Covasim: an agent-based model of COVID-19 dynamics and interventions. PLOS Comput Biol. 2021;17:e1009149.
Hinch R, Probert WJ, Nurtay A, Kendall M, Wymant C, Hall M, et al. OpenABM-Covid19—An agent-based model for non-pharmaceutical interventions against COVID-19 including contact tracing. PLoS Comput Biol. 2021;17:e1009146.
Manzo G. Matthews T. Potentialities and limitations of agent-based simulations. Rev française de sociologie. 2014;55:653–88.
Troitzsch KG. Analysing simulation results statistically: does significance matter? Interdisciplinary applications of agent-based social simulation and modeling: IGI Global; 2014. p. 88-105.
Milne GJ, Kelso JK, Kelly HA, Huband ST, McVernon J. A small community model for the transmission of infectious diseases: comparison of school closure as an intervention in individual-based models of an influenza pandemic. PLOS ONE. 2008;3:e4005.
Hussein T, Löndahl J, Thuresson S, Alsved M, Al-Hunaiti A, Saksela K, et al. Indoor Model Simulation for COVID-19 Transport and Exposure. Int J Environ Res Public Health. 2021;18:2927.
Lelieveld J, Helleis F, Borrmann S, Cheng Y, Drewnick F, Haug G, et al. Model calculations of aerosol transmission and infection risk of COVID-19 in indoor environments. MDPI AG; 2020. p. 1-18.
Vuorinen V, Aarnio M, Alava M, Alopaeus V, Atanasova N, Auvinen M, et al. Modelling aerosol transport and virus exposure with numerical simulations in relation to SARS-CoV-2 transmission by inhalation indoors. Saf Sci. 2020;130:104866.
Vecherin S, Chang D, Wells E, Trump B, Meyer A, Desmond J, et al. Assessment of the COVID-19 infection risk at a workplace through stochastic microexposure modeling. J Exposure Sci Environ Epidemiol. 2022;32:712–9.
Zhang X, Sun G-Q, Zhu Y-X, Ma J, Jin Z. Epidemic dynamics on semi-directed complex networks. Math Biosci. 2013;246:242–51.
Park SY, Kim Y-M, Yi S, Lee S, Na B-J, Kim CB, et al. Coronavirus disease outbreak in call center, South Korea. Emerg Infect Dis. 2020;26:1666.
Stehlé J, Voirin N, Barrat A, Cattuto C, Colizza V, Isella L, et al. Simulation of an SEIR infectious disease model on the dynamic contact network of conference attendees. BMC Med. 2011;9:87.
Albert R, Barabási A-L. Statistical mechanics of complex networks. Rev Mod Phys. 2002;74:47.
Acknowledgements
We are grateful to anonymous reviewers whose comments and suggestions allowed authors to improve the manuscript. This paper is based upon work supported by the Installation Technology Transfer Program. The views and opinions expressed in this article are those of the individual authors and not those of the U.S. Army or other sponsor organizations.
Author information
Authors and Affiliations
Contributions
SV is the author of the technical ideas and theoretical development of the method, AM is a lead developer of the code and data analyst, CC and BT are public health advisors, CE is installation safety specialist and consultant, and IL is general manager and senior advisor.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Ethics approval and consent to participate
No human or animal subjects were used in the study. The considered cases represent realistic, but virtual scenarios created for a hypothetical student campus.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Vecherin, S.N., Meyer, A.C., Cummings, C.L. et al. Infection risk assessment for socially structured population using stochastic microexposure model. J Expo Sci Environ Epidemiol (2025). https://doi.org/10.1038/s41370-025-00811-0
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41370-025-00811-0