Abstract
Secure information retrieval is an essential task in today’s highly digitised society. In some applications, it may be necessary that user query’s privacy and database content’s security are enforced. For these settings, symmetric private information retrieval (SPIR) could be employed, but its implementation is known to be demanding, requiring a private key-exchange network as the base layer. Here, we report for the first time a realisation of provably-secure SPIR supported by a quantum-secure key-exchange network. The SPIR scheme looks at biometric security, offering secure retrieval of 582-byte fingerprint files from a database with 800 entries. Our experimental results clearly demonstrate the feasibility of SPIR with quantum secure communications, thereby opening up new possibilities in secure distributed data storage and cloud computing over the future Quantum Internet.
Similar content being viewed by others
Introduction
Streaming a video on streaming platforms, checking a patient’s health records, and verifying one’s banking statements—these are all examples of information retrieval (IR), where the goal is to retrieve an entry of interest from an online database. While IR tasks are straightforward to implement, with users sending queries for their desired entries and the data centre responding with the correct information, it becomes challenging when there are privacy concerns. Indeed, from the user’s perspective, he/she may not want the data centre to learn about the query of interest for privacy reasons. For instance, the user may not want his/her video preferences to be known by the streaming platform, which can use such information for targeted advertisements. On the other hand, the data managed by the data centre could be sensitive or require long-term security, such as health records or bank account details. As such, these data centres would ideally want other entries of their database to be private from the user.
For tasks requiring both user privacy and database privacy, one can turn to symmetric private information retrieval (SPIR), which was first proposed by Gertner et al.1. SPIR guarantees that while performing IR, we have that (1) the data centre cannot learn about the user’s query and (2) the user cannot learn more about the database other than the requested information. However, while SPIR can provide strong security guarantees, its implementation is not straightforward. If there is only a single data centre for the user to communicate with, it is known that information-theoretically secure SPIR is impossible even with quantum resources2,3. As such, computationally secure SPIR protocols4,5,6,7 and cheat-sensitive quantum private query (QPQ) protocols8,9,10,11,12,13 have been proposed. However, computationally secure protocols may suffer from future advances in technology and QPQ does not provide the same strong security guaranteed by SPIR. Therefore, they may not be preferable choices for IR tasks aiming for an information-theoretic security, which is ideal for providing long-term security.
Towards achieving an information-theoretic secure SPIR, one can adopt the so-called multi-database scheme proposed by ref. 1. In this scheme, the user communicates separately with two or more data centres which holds the same database in order to successfully perform the IR task. If we assume that these data centres are non-communicating, it can be shown that the resulting SPIR scheme is information-theoretically secure1. For practical implementation of the proposed scheme, we require additionally that (1) information-theoretic secure communication channels exist between the user and data centres and (2) a random string is securely shared between the data centres. Both requirements can be satisfied with a secure key distribution scheme, since this key can be used directly as a shared random string or together with one-time pad (OTP) encryption for secure communication. However, classical key distribution schemes based on asymmetric cryptography rely on unproven assumptions, which could be weakened by theoretical or experimental advances14 and may not be preferable for SPIR aiming for an information-theoretic security.
To allow for practical implementation of SPIR, we turn to quantum key distribution (QKD), an information-theoretically secure method allowing network users to exchange secret keys. By exchanging quantum states and classical communication, QKD allows distant parties to securely generate shared keys which can be later utilised for the SPIR protocol. Since QKD is a relatively mature technology, with commercially available components, extensively-studied security analysis and well-developed post-processing algorithms15,16, it provides a basis on which SPIR can be built for practical implementation.
Results
Two-database SPIR
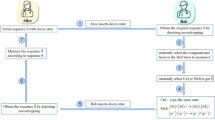
We consider here an IR scenario, where a user is interested in accessing the x-th entry of a database w, which contains n different entries wx (\(x \in \{ 1, \ldots ,n\}\)), of L bits each. In the corresponding two-database SPIR protocol, the user has to interact with two non-communicating data centres, D1 and D2, which each holds a copy of the database w. The protocol can be described as follows (also summarised in Fig. 1 with QKD as the key distribution protocol).
Key distribution
Secret keys are pre-distributed among the various parties in the SPIR protocol. We denote (K1, K2) as the key pair shared between the user and D1, (K3, K4) for the user and D2, and (K5, K6) for D1 and D2.
Query
The user prepares queries \(Q_i = f_{{{{\mathrm{query}}}},{{{\mathrm{i}}}}}(x,R)\), for data centre Di (\(i \in \{ 1,2\}\)), where R is a random string that is generated by the user locally. Subsequently, the user sends Q1 and Q2 to the respective data centres via OTP encryption with the secret keys K2 and K4, respectively.
Answer
After receiving the encrypted message, D1 and D2 first decode the transmitted information using keys K1 and K3. We note that the decrypted queries, \(\tilde Q_i\), may differ from Qi if the key pairs are not identical. Thereafter, data centres D1 and D2 generate answers \(A_1 = f_{{{{\mathrm{ans}}}},1}(\tilde Q_1,w,K_5)\) and \(A_2 = f_{{{{\mathrm{ans}}}},2}(\tilde Q_2,w,K_6)\), respectively. The answers A1 and A2 are then encrypted with keys K1 and K3 and sent to the user.
Retrieval
Upon receiving the answers from D1 and D2, the user decrypt the answers and recovers the desired database entry value with \(\hat w_x = f_{{{{\mathrm{dec}}}}}(\tilde A_1,\tilde A_2,Q_1,Q_2,x,R)\).
At the end of the SPIR protocol, four conditions should ideally be satisfied. (1) Correctness: The user should correctly recover his desired database entry, i.e. \(\hat w_x = w_x\). (2) User privacy: The data centres should not be able to determine the index of the database entry x which the user is interested in. (3) Database privacy: The user should not be able to gain any information beyond a single entry of the database. (4) Protocol secrecy: To protect the security of the data communicated, any external eavesdropper should neither be able to recover x nor any entry of the database w.
To achieve the aforementioned security conditions, the use of keys K1 to K6 are essential. Keys K1 to K4 serve as secret keys to encrypt communication between the user and the data centres, preventing any leakage of information to an external eavesdropper or the other data centre that may compromise user privacy and protocol secrecy. Keys K5 and K6 shared between the data centres are used by the data centres to implement private simultaneous message (PSM) and conditional disclosure of secrets (CDS) protocol1. The PSM protocol reveals the result of a function computation (\(\hat w_x\)) while masking the bits of the inputs to the function (\(\tilde A_1\) and \(\tilde A_2\)). The CDS protocol reveals a secret (\(\hat w_x\)), only if certain conditions are met (valid queries). Therefore, CDS forces a dishonest to provide honest queries while PSM prevents the user from gaining information about the database from the replies directly by forcing them to implement the appropriate fdec. When combined, both ensure that the user is only able to retrieve at most one entry of the database, even if the user is dishonest1.
In this paper, we focus on having an information-theoretic SPIR protocol, which requires the keys to be distributed with information-theoretic security. Having an information-theoretic secure protocol is ideal for data requiring long-term security, such as biometrics and health records, because it hedges against the threat posed by technological advancement. As computing power increases, quantum computers become more powerful, and novel algorithms are developed, many computationally secure protocols are at risk of being broken, which leads to leakage of information to external eavesdroppers. Hence, we require an information-theoretic key distribution protocol to maintain the security of SPIR.
SPIR with MDI QKD
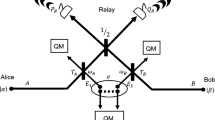
Since information-theoretic secure key distribution is impractical in the classical regime, we propose using QKD to distribute the necessary keys in an information-theoretic secure manner for use in SPIR. The overall SPIR scheme involves running SPIR with the aid of QKD generated keys, as presented in Fig. 2a. In this scheme, there is a QKD layer responsible for secure key distribution among distant parties with quantum transmitters and receivers. This QKD layer would supply the keys into an application layer upon which the SPIR protocol is implemented. Having this modular structure allows us to not only be flexible in the choice of QKD and SPIR protocols, but also allows other applications, such as secure communication channels, to be built upon the same QKD layer. The formal security proof of the SPIR protocol with QKD keys can be found in ref. 17.
a The SPIR system comprises two layers, the QKD layer and the application layer, which operate independently except for the transfer of secret keys. In the QKD layer, quantum transmitters are paired for key distribution, which includes procedures of quantum state preparation, quantum state measurement, and classical post-processing. In the application layer, each party obtains and manages the generated secret keys for the implementation of the SPIR protocol. The black dashed arrows represent the direction of the classical communication, while the orange solid lines represent quantum channels for QKD. b Schematic of the MDI QKD implementation. LD laser diode, IM intensity modulator, PM phase modulator, BS beam splitter, AMZI asymmetric Mach–Zehnder interferometer, ATT optical attenuator, PL optical power limiter, OS Optical switch, PC polarisation controller, PBS polarising beam splitter, SNSPD superconducting nanowire single-photon detector
In such a SPIR scheme, the final system performance depends on the design for both the SPIR layer and the QKD layer, with two main considerations: practicability and implementation security.
Practicability is linked to the resources required for implementation. Factors such as the key length and the number of data centres required for SPIR, or the key rate and the topology of the QKD scheme, has to been considered when choosing suitable protocols for the desired application. For instance, the keys required for the SPIR protocol proposed in ref. 1. for an n-entry database with k data centres scales as \(O(n^{1/(2k - 1)})\). Therefore, for applications with large database sizes, having more data centres can be preferable as it can reduce the key requirements.
Implementation security is closely related to the design and deployment of the QKD layer. Although QKD promises an information-theoretic security for key distribution based on quantum physics, its practical implementation may not be able to fulfil the security conditions perfectly. For example, a finite optical isolation of the quantum transmitter from the outside environment may result in vulnerability to Trojan-horse attacks18,19.
As such, we choose to deploy MDI QKD with decoy states for the QKD layer as it provides a great balance between practicability and implementation security20,21. In MDI QKD, each party (user and data centres) holds a quantum transmitter, which needs to be secured. The parties can then communicate via a central quantum receiver, which need not be secure and can be managed by external parties. This gives MDI QKD an appealing feature of immunity against any potential side-channel attacks on the quantum receiver, which is typically regarded as the most vulnerable part in practical QKD implementation16,20. As an added advantage, MDI QKD provides a natural star topology, making it suitable for network extension.
The MDI QKD protocol used has a key rate of21
where h(x) is the binary entropy of x, n0 is the number of events where either party sends zero photons, n1 is the number of events where both parties send one photon each, e1 is the error rate of these one-photon events, leakEC is the number of leaked bits from error correction, and the various ε values are security parameters.
For the SPIR layer, we consider the two-database SPIR protocol proposed in ref. 1 (detailed also in Appendix B of ref. 17). For a database with n entries of length L, the protocol requires \(\lceil{7L + \lceil{3}}\log m\rceil + (3 + 3L)m\rceil\) bits of key for secure communication between the user and each data centre, and (\(9Lm + 10L\)) bits of key for use as shared random bits between the data centres, where \(m = \lceil{n^{1/3}\rceil}\).
SPIR demonstration on fingerprint database
Here, we built up a MDI QKD system, and demonstrate the SPIR scheme with MDI QKD keys using a fingerprint minutiae database (containing only key features of the fingerprint) stored in the ISO 19794-2 standard format22. The database chosen is DB1A of the Fingerprint Verification Competition 200223, which is converted into minutiae data by Kayaoglu et al.24. It contains 800 entries (n = 800) and the maximum file size is 582 bytes (L = 4656). As such, \(1.72 \times 10^5\) bits of secret keys is required between the user and each data centre and \(4.66 \times 10^5\) shared random bits is required between the two data centres.
To verify the feasibility of the application, we first study its performance using a key rate simulation21,25,26,27. Using realistic parameters obtained from the MDI QKD system, with security parameters \(\varepsilon _{corr} = 1 \times 10^{ - 15}\) and \(\varepsilon _{sec} = 1 \times 10^{ - 10}\), we optimise l in Eq. (1) over the intensities \(\mu _1\), \(\mu _2\), \(\mu _3\), the probability of choosing an intensity and basis combination, the number of bits used for parameter estimation, and various security parameters. The performance of two cases are simulated. In the first case, we study our current MDI QKD system with a working frequency of 125 MHz and a run time of 13 h, generating \(N = 5.85 \times 10^{12}\) signal pulses in total. We also take the SNSPD counting rate saturation into consideration, which limits the value of \(\mu _1\) to a maximum value that varies with transmission distance. In the second case, we study our current MDI QKD system, but set at a working frequency of 1.25 GHz28 and a run time of 0.5 min, generating \(N = 3.75 \times 10^{10}\) signal pulses. In addition, high counting rate single-photon detectors are assumed for quantum state measurement29,30. In this case, the photon counting saturation issue is negligible, and there is no constraint on the value of \(\mu _1\). The simulation results are shown as the blue and red curve in Fig. 3a for the two cases. In both cases, the final key length generated is sufficient to meet the key requirement of the SPIR protocol (labelled by dotted lines) at a 50 km transmission distance.
a The blue curve is the simulated secure key length with \(N = 5.85 \times 10^{12}\) signal pulses (13 h operation of 125 MHz system) and with detector saturation under consideration. The red curve is the simulated secure key length with \(N = 3.75 \times 10^{10}\) signal pulses (0.5 min operation of 1.25 GHz system) and with no intensity limitation for quantum state preparation. The dotted lines indicate the number of keys required for the fingerprint database (\(4.66 \times 10^5\) shared bits of randomness between data centres and \(1.72 \times 10^5\) shared secret bits between the user and each data centre). b Demonstration of the fingerprint retrieval
We use the optimised parameters in the first case for our MDI QKD system to perform the experiment. After the quantum state preparation and quantum state measurement stated in Sec. Experimental details of MDI QKD, we first obtain raw keys as well as all the necessary statistics for key rate calculation. Subsequently, we perform post-processing on the raw key, including basis sifting, error correction, and privacy amplification to obtain the final secure keys required for SPIR.
After basis sifting, 10.34% of the sifted keys are used for parameter estimation, where it was found that the average bit error rate when transmitting states in the Z basis (\(\left| 0 \right\rangle\) and \(\left| 1 \right\rangle\)) is 0.83%. Error correction is performed on the remaining sifted keys by using symmetric blind low-density parity-check (LDPC) code31. This error correction code achieves an average correction efficiency of \(f_{{{{\mathrm{EC}}}}} = 1.41\). We note here that a better efficiency performance could be achieved by utilising other LDPC schemes such as the one in ref. 32, or using interactive protocols, e.g. Cascade, which generally provides a higher efficiency in the low error rate region31,32. However, for the latter case, a finite-key analysis with two-way protocols is desired for a rigorous security proof33. Subsequently, the corrected keys undergo privacy amplification via Toeplitz hashing34 accelerated by fast Fourier transform to generate final keys that are secret and uniformly distributed.
After post-processing, \(l = 6.50 \times 10^5\) bits of final secure keys are extracted. Here, for our proof-of-concept demonstration, only two quantum transmitters are actually implemented and the same pair of generated keys are re-used for all three QKD links. Finally, we implement the SPIR protocol, and successfully retrieve a target fingerprint file (4656 bits) from the database.
Discussion
We have demonstrated experimentally that the overall SPIR scheme is feasible. However, it is important to note the necessary assumptions and conditions required for a proper implementation of the protocol.
Firstly, to ensure the security of the SPIR protocol, we assume that the data centres are non-communicating1,17. If the two data centres are allowed to communicate, they are then able to behave like a single entity, which renders the SPIR protocol insecure. To enforce this assumption in practice, we could expect that administrative network management and access controls be utilised to prevent unauthorised communications35,36.
Secondly, we assume that the QKD system operates independently from the application layer. More specifically, none of the parties involved in SPIR (user or data centres), should be allowed access to the internal components of the quantum transmitter, or control its operations. To enforce this, one can reasonably imagine that the quantum transmitters are properly sealed and shielded by the service provider.
Finally, we have to also consider additional assumptions related to the QKD implementation security. For instance, in MDI QKD, the quantum transmitters are assumed to be secure and inaccessible to the eavesdropper. As such, any attacks from the quantum communication channel should be kept under control. Fortunately, such problems have been studied as source-related attacks in the practical QKD security analysis, such as the Trojan-horse attack18,19, laser seeding attack37,38 and laser damage attack39. Since the eavesdropping light is injected into the quantum transmitter via the quantum channel, a countermeasure based on optical power control can be expected, such as optical power limiter40 and optical fibre isolators41.
Methods
Experimental details of MDI QKD
The experimental setup of the MDI QKD is shown in Fig. 2b. The quantum transmitter held by each party consists of a laser source section and a quantum state preparation section. In the laser source section, a distributed feedback laser diode is operated in the gain-switching mode to generate laser pulses with a repetition rate of 125 MHz. This allows each optical pulse to inherit an intrinsically random and independent phase42,43 required for decoy-state analysis44. An intensity modulator (IM) is used for further pulse carving, which generates optical pulses with 220 ps width. In the quantum state preparation section, the phase randomised optical pulses are split into earlier and later time-bins by an asymmetric Mach–Zehnder interferometer. Thereafter, the pulses are modulated by an IM, a phase modulator (PM) and optical attenuators to generate time-bin phase-encoded quantum states: \(\left| 0\rangle \right. = \left| e\rangle \right._{\mu _j}\), \(\left| 1 \rangle\right. = \left| l \rangle\right._{\mu _j}\), \(\left| 2 \rangle\right. = (\left| e \rangle\right._{\mu _j} + \left| l \rangle\right._{\mu _j})/\sqrt 2\), \(\left| 3 \rangle\right. = (\left| e \rangle\right._{\mu _j} - \left| l \rangle\right._{\mu _j})/\sqrt 2\), where \(|e\rangle\) and \(\left| l \right\rangle\) represent the early and late time-bin temporal modes, and \(\mu _j\), \(j \in \{ 1,2,3\}\), represents three different intensities for the purpose of decoy-state analysis. Finally, an optical power limiter40 (or optical isolators41) is used to limit the information leakage from the transmitter to the outside environment. The central wavelength of the laser diodes are fine-tuned with a precision of around 0.1 pm (corresponding to a frequency uncertainty of 12.5 MHz), which guarantees the indistinguishability in the spectral mode of the two quantum states. Moreover, as the quantum states are required to arrive simultaneously at the receiver, the laser pulse generation and signal modulations in each transmitter are all synchronised to the same master clock, with a timing delay configuration precision of 10 ps.
After going through a 25 km spooled optical fibre, the quantum states from each quantum transmitter arrive at the quantum receiver. In the quantum receiver, an optical switch works in a time-division multiplexing way to connect two of the three parties to the quantum receiver. After successfully linking two legitimate parties to the quantum receiver, the fibre optical polarisation controllers and polarising beam splitters in each path calibrate the state of polarisation of the incoming photons. Thereafter, a 50:50 fibre beam splitter and two superconducting nanowire single-photon detectors perform Bell-state measurement (BSM) on the input quantum states. Including the insertion losses of optical components and fibre connectors, the final effective quantum efficiency of the measurement devices is 70.73% on average.
After the BSM, the quantum receiver publicly announces the measurement results. The paired transmitters then perform the necessary data processing and negotiation over an authenticated classical communication channel, including basis sifting, error correction and privacy amplification, etc., to obtain the final identical secure keys.
After calibrating all the degrees of freedom of the independent quantum transmitters, the Hong-Ou-Mandel interference visibility is measured to be 0.48 (±0.015). The slight deviation from the theoretical value of 0.5 with coherent state inputs and perfect mode overlapping indicates a good indistinguishability of the generated quantum states, which is a prerequisite for high efficiency BSM and determines the performance of the MDI QKD system.
Conclusion
In this paper, we experimentally demonstrated a two-database SPIR scheme utilising keys from a MDI QKD system on a fingerprint database with 800 entries and a maximum of 582 bytes per entry. In this two-layered scheme, the QKD layer generates the necessary keys for the SPIR protocol in the application layer, where they are used for secure communication and as shared random bit strings. This allows for SPIR with a provable security, which satisfies the strong security guarantees that certain IR problems may require, especially ones that involves sensitive data or data requiring long-term security. Our proposed scheme, along with its demonstration here, thus illustrates the feasibility of the practical implementation of SPIR for tacking IR problems.
References
Gertner, Y. et al. Protecting data privacy in private information retrieval schemes. J. Comput. Syst. Sci. 60, 592–629 (2000).
Lo, H. K. Insecurity of quantum secure computations. Phys. Rev. A 56, 1154–1162 (1997).
Chor, B. et al. Private information retrieval. J. ACM 45, 965–982 (1998).
Stern, J.P. A New and Efficient All-Or-Nothing Disclosure of Secrets Protocol. in Advances in Cryptology — ASIACRYPT’98 (eds. Ohta, K. & Pei, D.) 357–371 (Springer, 1998).
Lipmaa, H. An Oblivious Transfer Protocol with Log-Squared Communication. in Information Security (eds. Zhou, J., Lopez, J., Deng, R. H. & Bao, F.) 314–328 (Springer, 2005).
Naor, M. & Pinkas, B. Efficient oblivious transfer protocols. Proceedings of the Twelfth Annual ACM-SIAM Symposium on Discrete Algorithms. 448–457 (Society for Industrial and Applied Mathematics, 2001).
Chou, T. & Orlandi, C. The simplest protocol for oblivious transfer. Proceedings of the 4th International Conference on Cryptology and Information Security in Latin America. 40–58 (Springer, 2015).
Giovannetti, V., Lloyd, S. & Maccone, L. Quantum private queries. Phys. Rev. Lett. 100, 230502 (2008).
Jakobi, M. et al. Practical private database queries based on a quantum-key-distribution protocol. Phys. Rev. A 83, 022301 (2011).
Rao, M. V. P. & Jakobi, M. Towards communication-efficient quantum oblivious key distribution. Phys. Rev. A 87, 012331 (2013).
Giovannetti, V., Lloyd, S. & Maccone, L. Quantum private queries: security analysis. IEEE Trans. Inf. Theory 56, 3465–3477 (2010).
Olejnik, L. Secure quantum private information retrieval using phase-encoded queries. Phys. Rev. A 84, 022313 (2011).
Li, J. et al. Practical quantum private database queries based on passive round-robin differential phase-shift quantum key distribution. Sci. Rep. 6, 31738 (2016).
Gisin, N. et al. Quantum cryptography. Rev. Mod. Phys. 74, 145–195 (2002).
Scarani, V. et al. The security of practical quantum key distribution. Rev. Mod. Phys. 81, 1301–1350 (2009).
Xu, F. H. et al. Secure quantum key distribution with realistic devices. Rev. Mod. Phys. 92, 025002 (2020).
Kon, W. Y. & Lim, C. C. W. Provably secure symmetric private information retrieval with quantum cryptography. Entropy 23, 54 (2021).
Gisin, N. et al. Trojan-horse attacks on quantum-key-distribution systems. Phys. Rev. A 73, 022320 (2006).
Vakhitov, A., Makarov, V. & Hjelme, D. R. Large pulse attack as a method of conventional optical eavesdropping in quantum cryptography. J. Mod. Opt. 48, 2023–2038 (2001).
Lo, H. K., Curty, M. & Qi, B. Measurement-device-independent quantum key distribution. Phys. Rev. Lett. 108, 130503 (2012).
Curty, M. et al. Finite-key analysis for measurement-device-independent quantum key distribution. Nat. Commun. 5, 3732 (2014).
ISO/IEC 19794-2:2011/AMD 2:2015: Information technology—Biometric data interchange formats—Part 2: Finger minutiae data — Amendment 2: XML encoding and clarification of defects. International Organization for Standardization, Geneva, Switzerland. https://www.iso.org/standard/61610.html.
Maltoni, D. et al. Handbook of Fingerprint Recognition. 2nd edn. (Springer-Verlag, 2009).
Kayaoglu, M., Topcu, B. & Uludag, U. Standard fingerprint databases: manual minutiae labeling and matcher performance analyses. Preprint at: https://arxiv.org/abs/1305.1443.
Yuan, Z. L. et al. Interference of short optical pulses from independent gain-switched laser diodes for quantum secure communications. Phys. Rev. Appl. 2, 064006 (2014).
Ma, X. F. & Razavi, M. Alternative schemes for measurement-device-independent quantum key distribution. Phys. Rev. A 86, 062319 (2012).
Wang, C. et al. Realistic device imperfections affect the performance of hong-ou-mandel interference with weak coherent states. J. Lightwave Technol. 35, 4996–5002 (2017).
Wei, K. J. et al. High-speed measurement-device-independent quantum key distribution with integrated silicon photonics. Phys. Rev. X 10, 031030 (2020).
Dauler, E. A. et al. 1.25-Gbit/s photon-counting optical communications using a two-element superconducting nanowire single photon detector. Proceedings of SPIE 6372, Advanced Photon Counting Techniques. 286–293 (SPIE, 2006).
Chen, J. P. et al. Twin-field quantum key distribution over a 511 km optical fibre linking two distant metropolitan areas. Nat. Photon. 15, 570–575 (2021).
Kiktenko, E. O. et al. Symmetric blind information reconciliation for quantum key distribution. Phys. Rev. Appl. 8, 044017 (2017).
Elkouss, D. et al. Efficient reconciliation protocol for discrete-variable quantum key distribution. Proceedings of 2009 IEEE International Symposium on Information Theory. 1879–1883 (IEEE, 2009).
Tomamichel, M. et al. Fundamental finite key limits for one-way information reconciliation in quantum key distribution. Quant. Inf. Process. 16, 280 (2017).
Krawczyk, H. LFSR-based hashing and authentication. Proceedings of the 14th Annual International Cryptology Conference. 129–139 (Springer, 1994).
Denning, D. E. R. Cryptography and Data Security. (Reading, Mass: Addison-Wesley Longman Publishing Co., Inc., 1982).
Kim, D. & Solomon, M. Fundamentals of Information Systems Security. 3rd edn. (Jones & Bartlett Learning, 2018).
Sun, S. H. et al. Effect of source tampering in the security of quantum cryptography. Phys. Rev. A 92, 022304 (2015).
Huang, A. Q. et al. Laser-seeding attack in quantum key distribution. Phys. Rev. Appl. 12, 064043 (2019).
Huang, A. Q. et al. Laser-damage attack against optical attenuators in quantum key distribution. Phys. Rev. Appl. 13, 034017 (2020).
Zhang, G. et al. Securing practical quantum communication systems with optical power limiters. PRX Quantum 2, 030304 (2021).
Lucamarini, M. et al. Practical security bounds against the Trojan-horse attack in quantum key distribution. Phys. Rev. X 5, 031030 (2015).
Kobayashi, T., Tomita, A. & Okamoto, A. Evaluation of the phase randomness of a light source in quantum-key-distribution systems with an attenuated laser. Phys. Rev. A 90, 032320 (2014).
Yuan, Z. L. et al. Robust random number generation using steady-state emission of gain-switched laser diodes. Appl. Phys. Lett. 104, 261112 (2014).
Tang, Y. L. et al. Source attack of decoy-state quantum key distribution using phase information. Phys. Rev. A 88, 022308 (2013).
Acknowledgements
This research is supported by the National Research Foundation (NRF) Singapore, under its NRF Fellowship programme (NRFF11-2019-0001) and Quantum Engineering Programme 1.0 projects (QEP-P2, QEP-P3, and QEP-P8).
Author information
Authors and Affiliations
Contributions
C.W., W.Y.K. and C.C.-W.L. designed the project. W.Y.K. and C.W. performed the simulation and parameter optimisation. C.W. built up the experimental setup, and carried out the experiments. H.J.N. and C.W. conducted the post-processing. All the authors contributed to the writing of the paper.
Corresponding authors
Ethics declarations
Conflict of interest
The authors declare no competing interests.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Wang, C., Kon, W.Y., Ng, H.J. et al. Experimental symmetric private information retrieval with measurement-device-independent quantum network. Light Sci Appl 11, 268 (2022). https://doi.org/10.1038/s41377-022-00959-6
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41377-022-00959-6
This article is cited by
-
More trust in networks, more secure keys
Light: Science & Applications (2025)
-
Quantum key distribution with chromatic codes
Light: Science & Applications (2025)
-
Error-Tolerant Measurement-Device-Independent Quantum Private Queries of Blocks
International Journal of Theoretical Physics (2024)
-
Symmetric private information retrieval supported by quantum-secure key-exchange network
Light: Science & Applications (2022)