Introduction

Schizophrenia is a complex mental disorder where various biological changes have been reported. One of the most consistent electrophysiological findings is decreased entrainment to external stimuli as measured by the intertrial phase coherence (ITPC) in EEG or MEG [1,2,3,4,–5]. Schizophrenia subjects show less coherence in their phase angles at different frequencies, i.e., ITPC in response to rhythmically presented stimuli as in steady state or oddball paradigms ([6] for a recent review). Moreover, these subjects show decreased attention with reduced ITPC in response to deviant tones embedded in standard tones that do not arouse attention [7,8,–9]. Recent research has demonstrated that decreased ITPC in schizophrenia correlated with decreases in P3b amplitude indicating that changes in power might be due to deficits in phase resetting of the spontaneous activity to an external stimulus [10]. While being a relatively consistent finding in schizophrenia, the exact neural mechanisms of such decrease phase-based entrainment remain yet unclear, however.

Recent evidence converges towards temporal imprecision in the millisecond range in schizophrenia. This has been demonstrated in both amplitude [2, 11] and phase [2, 12,13,14] during task related activity like steady state and oddball paradigms [6]. Further, phase related temporal imprecision has also been demonstrated in the brain’s spontaneous activity as measured in EEG [13, 15]. However, given that phase cycles in for instance the theta range of 3.5 to 8 Hz last around 150 to 200 ms, it sheds some doubt on the utility of ITPC measuring temporal imprecision in the millisecond range of around 10 to 100 ms or even shorter than 10 ms as suggested in recent psychological studies [16,17,18,–19].

To better measure temporal imprecision in the shorter millisecond ranges, we recently introduced the precision index (PI) [6]. Similar to ITPC, the precision index measures the consistency of the phase cycles of individual trials in response to a stimulus. In contrast to ITPC, it is not computed as the variance of the phases across trials but as the interquartile range of the phase angles over trials. This has the advantage of disregarding bigger phase jumps and thereby allows one to capture the shorter millisecond phase dynamics [6] dynamics (see methods section for more detail). The first specific aim of our study was, thus, to test the newly introduced PI in a larger group of schizophrenia subjects in a typical auditory oddball paradigm focusing specifically on the deviant tones. We hypothesized that the PI would be significantly decreased in the schizophrenia subjects compared to a healthy control group in specifically the deviant tones thus indexing smaller millisecond phase cycles changes in a temporally more precise way than the standardly used ITPC.

Yet another limiting factor of the ITPC (and by extension the PI) consists in the need to average across trials. Ideally one would be able to extract pertinent phase information from single trials. However, as is the case with all event-related EEG measures, the signal-to-noise ratio does not allow for such single-trial analysis (see [3] and [11] for single-trial analysis attempts to circumvent this limitation). ITPC and PI are therefore calculated from tens to hundreds of trials which are averaged to suppress the noise and highlight the signal similarities across several of the same trials. Commonly, the ITPC is usually calculated in a static way (sITPC) over a window of tens to hundreds of milliseconds and over an entire frequency band or even across frequency bands from all standard or deviant trials. Such averaging, however, introduces a high degree of temporal smoothing by eliminating – or averaging-out – millisecond temporal imprecisions in the latencies of and between the single trials. The dynamical changes in the phase latencies varying from trial to trial, that is, between the single trials are lost in such static approach. We tackle this methodological insufficiency by introducing a novel dynamic windowed approach to calculating the ITPC in an auditory oddball paradigm, a dynamic intertrial phase coherence (dITPC). For that purpose, we use a heuristic where we construct a sliding window containing 100 trials, regardless of whether these trials are standard or deviant tones, with an offset, e.g., step size of one trial between the sliding windows. This enables us to measure temporal imprecision in the millisecond range of both latency and frequency of the dITPC. Introducing such a dynamic approach to the ITPC as well as measuring its latency and frequency in both healthy and schizophrenia subjects was thus the second specific aim of our study. We hypothesized that schizophrenia subjects show higher latency and frequency in such dITPC compared to healthy subjects.

Given its window-based calculation, the dynamic ITPC is measured across the entire EEG recording, i.e., all trials including both standard and deviant tones. This raises the question whether its dynamic features, e.g., changes in latency and frequency over time, are related to the temporal imprecision in specifically the deviant tones as measured by the precision index. Conducting regression analyses between dITPC and the PI was thus the third specific aim of our study. We hypothesized that temporal changes in the phase cycles over time, as captured by the increased latency of the dITPC in schizophrenia subjects, would predict their temporal imprecision in the PI. This would further specify the nature of temporal imprecision in that it may be related to abnormally dynamical changes in the millisecond ranges of the phase related latency over time. Moreover, it may provide a first step toward establishing a background–foreground relation on the neuronal level [20]. Specifically, millisecond changes in phase latencies over the course of time across both standard and deviant tones, i.e., dITPC, may serve as dynamic background for the temporally imprecise response to the cognitive attention task during the deviant tone, i.e., PI. This is relevant given that an analogous background–foreground relationship has already been discussed on both psychological, i.e., perceptual [21, 22] and psychopathological [23] levels of schizophrenia.

Materials and methods

Subjects

We analysed 54 schizophrenia 32.78 ± 7.59 years, 30 female) patients and 113 healthy controls 37.52 ± 11.84 years, 55 female). All patients were recruited from the outpatient clinics and day-care units of the Department of Psychiatry, National Taiwan University Hospital. Age- and gender-matched healthy controls were recruited in the same study approved by the National Taiwan University Hospital Institute Review Board (IRB number: 200812098 R). Written informed consent were acquired from all participants before any experimental procedures. The general inclusion criteria were 1) age between 18 and 65 years old, 2) no mental retardation or major brain pathology, 3) no debilitating systemic diseases, 4) passing a hearing screening test by audiometry over 500 Hz, 1000 Hz and 6000 Hz. Patients had to be diagnosed with schizophrenia by one board-certified psychiatrist according to the DSM-4 [24]. Patients with schizoaffective disorders, bipolar affective disorders, organic mental disorders, or substance-related disorders (except for tobacco) were excluded. Healthy subjects must have no current or lifetime major mental disorders (schizophrenia, schizoaffective disorder, bipolar disorder, major depressive disorder) and substance-related disorders (except for tobacco), assessed by research assistants according to the Chinese version of Diagnostic Interview for Genetic Study (DIGS) [25].

Experimental procedure

The participants received EEG experiments within a sound-attenuating, electrically shielded booth. They were instructed to be seated in a comfortable recliner watching soundless neutral cartoons on an eye-level 19-inch LCD monitor screen in front of them. They were instructed to minimize eye movements and facial muscle tension as well. An auditory oddball paradigm was adopted to elicit duration mismatch negativity (MMN). Binaural auditory stimuli consisted of 90% standards and 10% deviants. Both standards and deviants were 85-db and 1000-Hz pure tones, while the former were 50-ms long and the later 100-ms long. Standards and deviants were presented in a pseudorandom order, and the onset asynchrony between stimuli was 500 ms. Subjects were observed through a video monitor throughout the EEG experiments. When sleepiness was noted by visual inspection or indicated by EEG slow waves, an experimenter would speak briefly with them to enhance arousal. For details of the EEG recording setup and preprocessing refer to the Supplementary Material.

Calculation of static intertrial phase coherence (sITPC)

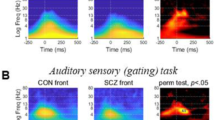
ITPC was calculated via MNE (v1.31) python’s Morlet Wavelet convolution (time_frequency.tfr_morlet), with the number of cycles configured to half of each frequency [26]. Forty-five logarithmically scaled frequencies ranging between 1.3 and 45 Hz were selected for ITPC extraction, with cycle durations set to half of each frequency. The window for extraction of the ITPC values for statistical analysis was based on the visual inspection of the averaged time-frequency plot of healthy controls (Fig. 1) and was set as an average of the window in the theta and alpha ranges between 4 and 12 Hz, and 0.1 and 0.4 seconds. Due to the dynamic analysis of ITPC outlined below, we chose to calculate ITPC for all standard as well as all deviant trials. We also calculated Spearman correlations of sITPC and peaks related to the intertrial interval in the power spectral density. This analysis can be found in the supplementary material.

Fig. 1
figure 1

Calculation of dynamic intertrial phase coherence (dITPC) and hypothesis of the study.

Full size image

Intuition of precision index (PI)The precision index is a measure of variability, different from the variance calculated in the ITPC. It is a measure of how spread the phase angles are across trials. If the brain aligns temporally precisely to the external stimulus, phases across all trials will cluster around the same or similar phase angles. In contrast, if the alignment is temporally imprecise, single-trial phases will inhabit a larger range of angles. The PI measures the spread, that is the interquartile range (IQR) of phase angles that align to the stimulus. Lower quartile (LQR) and upper quartile ranges (UQR) are inhabited by phases that represent large outliers from the mean phase angle responses (see Fig. 2). Measuring the narrow IQR range of phase angles within this narrow range then allows to make group distinctions within the range of phase alignment necessary for stimulus processing. Since the normalized IQR is subtracted from one in the precision index calculation, and a small IQR represents a smaller range of the average phase angles, a higher PI represents higher precision. Conversely, when subtracting a larger IQR range, i.e. a wider range of average phase angles, from 1, the PI will be smaller. The PI therefore measures more minute phase differences within the mean range of phase angles and is therefore a useful measure of phase alignment in the millisecond range. If the IQR range is larger, i.e. there is a lower precision index, that indicates that phase responses are less precise within a small range of phase angles. If phases were perfectly aligned over all trials, the IQR, measured by the distance between the third and first quartile would shrink close to zero and the PI would be close to 1. If the phases show no alignment the IQR will be large and in effect the precision index will be small. It is important to note that the lower and upper quartile ranges do not indicate large and small deviations from the mean, respectively. Since phase angles are circular, the lower quartile range can be thought of phase angles that are shifted furthest to the negative of the mean, while upper quartile range are phase angles shifted furthest to the positive of the mean. However, both represent outliers from the average phase response to the stimulus over trials. [6] (for a graphical depiction of this intuition see Fig. 2). Since the ITPC measures the full range of phase cycles it is naturally less adequate to measure the minute millisecond changes since it also includes all outliers in its variability calculation.

Fig. 2: Intuition of precision index as the Interquartile range of phase angles over trials.
figure 2

Subtle changes in phase dynamics cause decreased alignment to the stimulus in single trials. This decreased alignment is measured by the PI as consistency of the phase over trials in the IQR. The narrow range of average phase responses allows for better short millisecond range characterization compared to the classical ITPC.

Full size image

Calculation of the precision index (PI)

Epoched data were transformed via complex Morelet Wavelet convolution. As in the sITPC analysis, the number of cycles was half of the frequency for 45 log-spaced frequencies between 1.3 and 45 Hz. Since an unequal number of trials per patient would bias the PI, number of trials for the calculation was set to smallest trial count found in any subject, which was 1934 for standard and 219 for deviant stimuli. We calculated the interquartile range (IQR) of phase angles and divided them by the number of trials and subtracted the average from 1 to obtain precision index values. In accordance with previous literature [6], we extracted values between 4 and 6 Hz and 250 to 350 ms, as tested in auditory paradigms. Frequencies below 4 HZ were deemed unreliable because, with an inter-stimulus interval of 500 ms, there would not be enough cycles needed for computing ITPC. To further confirm that schizophrenia patients have deficits in the millisecond range in their phase alignments, we also calculated group differences for the LQR and UQR. We expected that decreases in precision in schizophrenia would be present only in the IQR, but not in the LQR and UQR.

Lower quartile range (LQR) and upper quartile range (UQR), defined as the 0th to 50th and 50th to 100th percentile, respectively for the same time-frequency window. We calculated group differences in those ranges as well as differences between the 3 ranges within groups using ANOVAs and post hoc tests for individual differences within each range. Student’s t-tests were used to compare each range-based PI between healthy controls and schizophrenia. Last we were also interested in the differences between IQR and LQR and between IQR and UQR. Therefore we calculated absolute differences between the range-based PIs and compared then between healthy participants and schizophrenia patients.

Calculation of dynamic intertrial phase coherence (dITPC) via a sliding window

Since we assume that schizophrenia patients suffer from dynamic changes in their response to stimuli, we went beyond the traditionally static way of calculating ITPC. We calculated ITPC for 100 consecutive trials, regardless of whether they were standard or deviant tones with an offset of 1 trial per sliding window (Fig. 2). This allowed us to investigate the dynamics of the phase coherence in response to the stimuli, hereafter referred to as dynamic intertrial phase coherence (dITPC). From each window we extracted three values, 1) maximum value between 4 and 12 Hz and between 0.1 before and 0.4 seconds after trial onset, 2) the latency at which this value occurred, as well as 3) its frequency. Increased time and frequency ranges were chosen to find the maxima between 100 ms before and 450 ms after stimulus onset and between 4 and 12 Hz. For both latency and frequency, the mean and variability, i.e., the coefficient of variation (CV) were calculated. All values were calculated for electrode Cz given the auditory nature of our paradigm.

While behavioural response times are consistently reported to be delayed in schizophrenia patients [27], the attempt to link them to latencies of event-related potentials has not conclusively linked behaviour with its electrophysiological underpinnings [1, 28, 29]. ERP latencies differ for different ERP components: Earlier components associated with basic perceptual processing are reported to show differences in amplitude [30,31,–32] compared to healthy controls, although latencies of peak amplitudes have not been conclusively demonstrated to be prolonged in schizophrenia [33]. However, there is some evidence that the P300 component shows delays in schizophrenia patients in comparison to control subjects, but these effects are considerably lower than in amplitude differences [34, 35]. Importantly, the P200 complex which is associated with prediction shows increased temporal irregularities [11]. Also, a recent study has directly linked ERP amplitude to decreased ITPC in schizophrenia [10].

Differences and changes in the frequencies involved in averaging for the ITPC are not usually target parameters in studies using ITPC. Reports of decreased phase coherence and spectral power has been consistently demonstrated in schizophrenia, such as in delta, alpha, theta, beta and gamma frequency bands [2,3,4,–5, 14, 36,37,38]. However, shifts of phase coherence or power from one frequency to a higher or lower frequency has to the best of our knowledge not been investigated before. Since the choice of upper and lower frequency bounds for the averaging window might have an influence of ITPC values, we want to investigate this parameter as well. It is possible that fluctuation in coherence across frequencies could impede the reliability of ITPC calculation. Due to the lack of literature in frequency shifts in phase coherence (and spectral power), the investigation of frequency shifts remains exploratory.

Statistical analysis

Group comparisons and normality

We tested for normality and homogeneity of variance of the variables under investigation, i.e. sITPC, PI and dITPC latency and frequency, as well as age and years of education. Based on the results we used Mann-Whitney U tests to test for group differences of sITPC. Chi-square test was used to calculate the sex differences between the two groups.

The normality and equality of group variances allowed for parametric t-tests to be used for group comparisons of precision index as well dITPC latency and frequency. We additionally computed Cohen’s d effect-sizes for the group differences. We also tested the relationship of sITPC and PI, by computing Spearman correlations (Supplementary Figure 1).

Furthermore, we investigated whether dITPC latency and frequency had any predictive power for PI. Because covariates and education showed inequality of variances between the groups and education additionally was not normally distributed, we used the non-parametric robust linear model (RLM) with a conservative t-value of 4 as tuning constant for Hubert’s function, which is a robust regression method that is less sensitive to outliers, normality and skewness by substituting the normal distribution with a heavy-tailed distribution. First, we investigated predictability within each group separately. Then we compared the predictive value across groups, by including an interaction term group*measure. Age, sex and years of education were entered as covariates into the model at each time. PI was scaled up by 1000 for each model to counterbalance very small regression coefficients and make results more human-readable.

All statistical analyses were performed using the Python packages statsmodels (version) or scipy (version).

Results

Demographics

The age distribution was normal for schizophrenia patients (W = 0.96, p = 0.13) but not for healthy controls (W: 0.96, p = 0.002) and non-normal for both groups in years of education (HC: W = 0.92, p = 0.0, SZ: W = 0.92, p = 0.001). Groups differed in terms of variance in both age (F(1,164) = 11.18, p = 0.001) and years of education (F(1,165) = 5.15, p = 0.025). In terms of sex groups did not significantly differ (χ2 = 0.73, p = 0.39). However, healthy control subjects (37.65 ± 11.84 years) were on average older than schizophrenia patients (32.38 ± 7.59 years, U: 3632.5, p: 0.01). Furthermore, control subjects (15.65 ± 1.99 years) had longer education time than patients (14.52 ± 2.39 years, U = 3614.0, p = 0.01). Given these differences, we included these variables as co variates in all subsequent analyses.

Static intertrial phase coherence (sITPC)

We first calculated the standard measure of phase coherence over all trials of standard and deviant tones respectively in a static way, i.e., sITPC. Values of deviant sITPC were not normally distributed (HC: W = 0.095, p < 0.0001, SZ: W = 0.83, p < 0.0001) and the groups showed differences in their variances (F(1,162) = 7.82, p = 0.006. We therefore used non-parametric Mann-Whitney U tests to compare the groups. Healthy participants had significantly stronger coherence (U = 428.0, p < 0.0001) in their phases in response to deviant stimuli (HC: 0.19 ± 0.08), compared to schizophrenia patients (SZ: 0.13 ± 0.06) in the theta range between 0.1 and 0.4 seconds. Similar decreases in schizophrenia were found for the standard stimuli (see supplementary material). Together, these results replicate previous findings.

Precision index

Next, we were interested in a temporally more precise index of phase coherence that better captures temporal changes in the millisecond range, for that purpose we calculated the precision index. Data were normally distributed (HC: W = 0.98, p = 0.21, SZ: W = 0.97, p = 0.3) and showed equal variances (F(1,164) = 0.5, p = 0.56) for both groups. Student’s t-tests revealed significantly higher PI for healthy control subjects (0.990 ± 0.00255) compared to schizophrenia patients (0.988 ± 0.00249; t(164) = 5.35, p < 0.00001, d = 0.9; Fig. 3) in the deviant tone. No difference was found in the standard tones (see Supplementary Figure 2). To test the relationship between PI and sITPC we computed their spearman correlations. We found that the two measures correlate for deviant tones, but not in standard tones in both groups. Correlations were only r(112) = 0.9, p < 0.0001 for HC and r(52) = 0.7, p < 0.0001 for SZ. Together, these findings suggest that the PI and the sITPC are related but not identical. Albeit indirectly, this further supports their differences in capturing distinct temporal features of the phase cycles which, in turn, further highlights the phase related temporal deficits in the lower millisecond range in schizophrenia (see also Wolff & Northoff 2024).

Fig. 3: Precision index.
figure 3

PI for healthy controls and schizophrenia patients. A The red square indicates the time (0.25 s to 0.35 s) and frequency ranges (4 Hz to 6 Hz) for which the IQR-based PI was calculated. B Group differences between the 3 PIs based on quartile ranges LQR, IQR and UQR.

Full size image

To test whether the IQR was indeed the best candidate for finding group differences, we also calculated lower and upper quartile ranges. Neither LQR (t(164) = − 1.57, p = 0.12) nor UQR (t(164) = 1.15, p = 0.25) showed significant group differences between healthy and schizophrenia participants. We further calculated ANOVAs for both groups to investigate whether IQR-based PI was significantly different from LQR- and UQR-based PI. We found that the three PIs showed significant differences in both HC (F(1,164) = 322.9, p < 0.0001) and SZ (F(1,164) = 74.26, p < 0.0001). Post hoc test revealed differences for each of the quartile range-based PIs for HC but a lack of differences between IQR and UQR for schizophrenia patients (See Supplementary Table 1). Last, we also calculated absolute LQR − IQR and UQR − IQR differences and compared them between healthy controls and patients. We found that IQR − LQR 4.6 p < 0.0001) and IQR − UQR (t = 4.43, p < 0.0001) differences were larger for healthy controls.

Dynamic ITPC latency and frequency

In a next step, we raised the question whether the observed millisecond range temporal deficit in schizophrenia, as measured by the PI in response to deviant tones, relates to continuously ongoing temporal irregularities in the phase cycles over the course of time across both standard and deviant tones. In order to capture such dynamics of temporal phase irregularities, we calculated the ITPC in a dynamic way, i.e., dITPC, including both its latencies and frequencies.

The latency values from the dITPC sliding windows were normally distributed (HC: W = 0.98, p = 0.14, SZ: W = 0.98, p = 0.33) and showed equal variances (F(1,164) = 1.89, p = 0.17) for both groups. Student’s t-test revealed significantly longer latency values for SZ (0.186 ± 0.027 s) than HC (0.176 ± 0.029 s; t(164) = − 2.07, p = 0.04, d = −0.35, Fig. 4 left).

Fig. 4
figure 4

Group differences between dITPC latency (left) and frequency (right).

Full size image

Frequency values were also normally distributed (HC: W = 0.98, p = 0.099, SZ: W = 0.98, p = 0.69) and also showed equal variances (F(1,164) = 0.29, p = 0.59) for both groups. Student’s t-test revealed significantly higher frequency for SZ (17.14 ± 3.96 Hz) than HC (15.56 ± 3.96 Hz; t(164) = − 2.41, p = 0.017, d = −0.4, Fig. 4 right). Together, these findings show changes in the ongoing phase dynamics in schizophrenia across both standard and deviant tones concerning both its temporal, i.e., latency, and frequency components.

dITPC latency predicts precision index

We so far showed phase-based temporal imprecision in the lower millisecond range in both the response to deviant tones as measured by the PI, and the continuously ongoing temporal irregularities as measured by the novel dITPC. This raises the question whether the continuously ongoing temporal irregularities over both standard and deviant tones are related to the temporal imprecision in response to the deviant tones. For that purpose, we now conducted regression model for linking dTIPC and PI.

The robust linear regression for HC and SZ separately revealed that dITPC latency predicts deviant PI (HC: β = −33.87, p < 0.001, SZ: β = −22.24, p = 0.05) when accounting for sex (HC: β = 0.64, p = 0.13), age (HC: β = −0.11 p < 0.001, SZ: β = −0.07, p = 0.18), and education (HC: β = 0.12, p = 0.24, SZ: β = 0.18, p = 0.24; Fig. 5a and b). In contrast, dITPC frequency did not show such a prediction in either group separately (HC: β = −0.08, p = 0.23, SZ: β = 0.06, p = 0.66) when controlling for age (HC: β = −0.008, p < 0.01, SZ: β = −0.07, p = 0.23), sex (HC: β = 0.58 p = 0.21, SZ: β = 0.0.22, p = 0.78) and education (HC: β = 0.17, p = 0.12, SZ: β = 0.16, p = 0.23).

Fig. 5: Results of regression models.
figure 5

Robust linear regression model results for dITPC latency (a, b) and dITPC frequency as calculated in a dynamic way including both deviant and standard tones (c, d) prediction of PI calculated from deviant trials.

Full size image

When including the interaction term group * dITPC latency into a combined group analysis the predictive value of dITPC latency showed significant group differences (β = −12.27, p < 0.001; Fig. 5c and d) when accounting for dITPC latency on its own (β = −25.87, p < 0.001), as well as age (β = −0.01, p < 0.001), sex (β = 0.74, p = 0.04) and education (β = 0.16, p = 0.05) as covariates. Even though dITPC frequency did not show a predictive value for PI for each group separately, nor for combined groups (β = 0.01, p = 0.91), the interaction term group * dITPC frequency showed significant group differences (β = −0.13, p < 0.001) when simultaneously accounting for age (β = −0.07, p < 0.001), sex (β = 0.36, p = 0.35) and education (β = 0.1, p = 0.05). As a control, we also computed reversed models to see whether deviant PI can predict both dITPC latency and frequency (Supplementary Figure 3) and repeated the analysis for PI of standard trials. These models did not show any similar significant results (see Supplementary Figures 4 and 5). Furthermore, we calculated bootstrapped intervals confidence from 10000 iterations for all coefficients iterations to further validate and increase the validity of our findings. The results of our analysis can be found in Supplementary Table 2.

Together, these findings indicate a special role of the latency of the ongoing phase dynamics across both standard and deviant trials in relating to and predicting the temporal imprecision of the phase in response to the attention demanding deviant tones, e.g., the precision index. More generally, this suggests that the continuously ongoing temporal irregularities over all trials shape the temporal imprecision during the cognitive task, e.g., the deviant tones.

Discussion

We here investigated phase dynamics in schizophrenia in a temporally more fine-grained way, that is, 1) more temporally precise using the novel precision index and 2) with a higher temporal resolution using a novel dynamic analysis of phase coherence. We show reduced precision index and higher dynamic fluctuations in both latency and peak frequency in schizophrenia with the latter predicting the former. Together, this suggests an altered dynamic background in the phase dynamics of schizophrenia leading to temporal imprecision in the lower millisecond range during cognitive function like attention in the foreground. Although tentatively, we conclude that schizophrenia can be characterized by abnormal phase dynamics with temporal irregularities in the background leading to temporal imprecision in the lower millisecond range in the more cognitive foreground.

First, we were able to reproduce and further corroborate evidence of decreased ITPC in the theta range in schizophrenia. The ITPC represents one of the most consistent biomarkers in schizophrenia and is believed to be a direct measure for temporal imprecision [6]. A failure to align the brains intrinsic oscillations to the stochastics of a task environment has been shown to be a key deficit in not only schizophrenia, but also other psychotic disorders, such as bipolar disorder [39], albeit to a lesser extent. Decreased ITPC in schizophrenia has recently been linked to ERP amplitudes. Usually decreased ERP amplitudes are discussed in the context of weakened recruitment of neural processing units. However, a recent paper has suggested that temporal imprecision can serve as a good explanation for these amplitude changes in schizophrenia. ERPs are calculated by averaging electric signals over trials. If the individual peaks per trial arrive at slightly different times, the net effect over trials will be decreased as well, showing as lower amplitudes [10]. Our goal in this study was to further refine these measures to gain better insight into the nature of the phase-based temporal precision in schizophrenia.

In this light, our second main finding is the usefulness of the precision index as a measure of temporal imprecision that can be a valuable addition to existing tools in the study of schizophrenia electrophysiology [6]. The major advantage of the PI over ITPC is that it allows for investigation in a limited range (interquartile range) of phase angle consistencies in response to a stimulus thus capturing temporally more precise the phase changes in a lower millisecond range. This is particularly useful since temporal imprecision has been shown to be altered in the lower millisecond range on psychological [40, 41], neuronal [13], and computational [2, 6] grounds. We demonstrate that in response to deviant, but not standard stimuli (see supplementary material), the temporal precision in the phase angles of the EEG is reduced in schizophrenia. To test whether schizophrenia have indeed problems in their average phase responses, we also calculated lower and upper quartile ranges. As expected, we found no group differences in these ranges, which contain larger deviants of the mean of the single trial phase responses. We interpret this finding to indicate that schizophrenia patients have difficulties with consistently temporally aligning to the external stimulus. LQR and UQR contain outliers that are included in the calculation of the ITPC. By demonstrating that deficits are constraint to the interquartile range, we argue that the ITPC might be contaminated with larger phase deviations that are equally present in healthy controls and schizophrenia patients. Therefore, the PI is a good complementary tool to better study phase variance in a smaller, i.e. millisecond temporal range. Our results can therefore be seen as corroborating evidence for such new temporally more precise measure in schizophrenia electrophysiology research [6]. We were further able to show that, while ITPC and PI are similar, they are not identical, as their relationship was only moderately strong (see Supplementary Figure 1).

To further probe the mechanism of temporal imprecision we investigated dynamic changes in the ITPC. Our third main finding is that there are dynamical changes within the monolithic construct that is the ITPC. Employing a dynamic windowed approach over the entirety of the EEG recording we were able to extract information of the latency and frequency of the phases in response to all stimuli. This allowed us to show both increases in both latency and frequency in schizophrenia patients, hinting towards difference in the ongoing phase dynamics in schizophrenia. More generally, these findings suggest ongoing temporal irregularities in the phase dynamics that accumulate in a dynamic way over time resulting in the higher frequency and latency of the dITPC.

Our finding of changes in the dynamics of ITPC led us to the final question whether those changes have an influence on statically calculated measures, such as the PI. Therefore, we combined the dynamic with the static approach and asked the question whether dynamic changes can predict precision calculated from all deviant trials. Our fourth main finding is that dITPC latency but not frequency predicts PI. This lends further support that phase-based temporal imprecision is indeed related to timing deficits. Since dITPC measures were calculated from the entirety of the recording they consisted of both standard and deviant measures, they can be seen as a dynamic background layer upon which processing of relevant (deviant) stimuli is overlayed on a more cognitive foreground layer. This suggests that phase coherence, a well-established biomarker for schizophrenia, might be caused or influenced by ongoing temporal irregularities of the phase dynamics in the background.

Such background-foreground interpretation, albeit tentatively, is in line with research on the perceptual domain. These findings suggests that the primary perceptual processes (foreground) in schizophrenia remain undisturbed by themselves but that they are embedded in an abnormal context (background) that leads to delusional perception [21]. Phenomenologically, schizophrenia patients may experience alterations of their perceptual field at large, in which correct perception are integrated wrongly and hence misinterpreted [22]. Our findings hint towards a possible underlying temporal mechanism, by showing that continuously ongoing temporal irregularities in the dynamic background can impair the temporal precision in the more cognitive foreground, i.e., the response to the deviant tones. This is even more remarkable given that the dynamic ITPC is calculated over the entirety of the recording, which naturally will include more standard than deviant trials while it nevertheless predicts the response to specifically the deviant tones, i.e., the PI deviant but not the one to standard tones. Though indirectly, this lends additional support to our hypothesis that what we measure with dITPC is the dynamic background, that has an influence on cognitive performance in the foreground, i.e. the detection of deviant tones in the oddball task.

Limitations

While there are some exceptions, latency is not commonly assessed in research of phase coherence [42, 43]. However, ERP studies have demonstrated that brain activity is delayed in response to external stimuli. Given the close relationship of phase information and ERP peak amplitudes [44], we reasoned that latency changes would also be present in the phase information. Indeed, dITPC latency showed delays in response to task in schizophrenia patients, mirroring findings on ERP amplitudes.

Interestingly, we were able to demonstrate for the first time that the peak phase coherence shifts towards higher frequencies in schizophrenia patients. When averaging over a time-frequency window for static ITPC analysis these nuances might be lost. These findings further have implications for analysis of spectral power. Future studies will have to demonstrate that decreases or increases in power in specific frequency bands simply represent a power decrease rather than a shift of peak power to other frequencies.

Furthermore, we did unfortunately not have a complete record of medication for the patient group and can therefore not completely rule out medication effects being responsible for some of the findings presented here. However, other studies of ours [2] and others [36] show that the inclusion of medication as co-variate does not essentially change the results, that is, eliminates the ITPC deficit.

Conclusion

Various lines of evidence converge towards temporal imprecision of phase related processes being a key pathophysiological feature in schizophrenia. We here extend and specify this hypothesis by showing that temporal imprecision occurs in the millisecond range, as measured by the novel precision index. Moreover, employing a novel analysis of phase dynamics, we show that temporal imprecision occurs in a dynamic way with high temporal irregularities with changing latencies and frequencies of the phase dynamics over and across trials.

Together, we demonstrate strong evidence for altered phase dynamics in schizophrenia with temporal imprecision in the smaller millisecond range around 10 milliseconds. This substantiates and specifies recent findings of a temporal disturbance in schizophrenia being a core pathophysiological feature. More generally, our findings are compatible with abnormal background foreground relation on the neural level of the brain. Schizophrenia seems to show abnormal phase dynamics in the background leading to millisecond temporal imprecision in the foreground during cognitive tasks like our attention demanding oddball task.