Introduction

Among vanadium oxides, VO2 stands out for its metal insulator transition (MIT)1 from a monoclinic insulating phase to a tetragonal metallic phase upon heating1,2,3 (with a transition temperature TC of 340 K in bulk), making it an ideal candidate for technological implementation. The concomitant occurrence of an MIT and a structural phase transition (SPT) sparked discussion over the nature of the MIT itself4,5,6,7,8. After decades of debate, the state-of-the-art dominant theoretical scenario is that of a cooperative orbital-assisted Mott‒Peierls mechanism9. The MIT in VO2 is interesting from a technological point of view because of its reversible 3–4 orders of magnitude resistivity jump across the transition10,11. These features enable applications such as smart windows and the development of new technologies spanning from neuromorphic devices to memristive devices12,13,14,15,16. In addition, the metallic phase of VO2 has multiband characteristics and is intrinsically anisotropic. The electronic structure and thus the resistive properties strongly depend on the crystal orientation17,18,19,20,21. This is an often overlooked aspect that may lead to new appealing applications, such as efficient ion migration and coupling in synaptic devices22, nanoactuators23 and the fabrication of dynamically reconfigurable optical elements24. The ability to control VO2 properties and, in particular, the electronic structure anisotropy is therefore of upmost importance to envision such implementations.

To understand the role of band anisotropy in the MIT properties, probing its electronic character close to the Fermi level (FL) in proximity to the phase transition is necessary. The high-temperature metallic phase of bulk VO2 has lattice tetragonal symmetry (often called rutile and indicated with R). In this phase, two bands populate the FL, \({d}_{{||}}{{-}}{\pi }^{* }\). \({d}_{{||}}\) is directed along the c axis (cr) and is composed of the superposition of a1g orbitals2. The \({\pi }^{* }\) band is formed by the antibonding band generated by the chemical bond between vanadium \({e}_{g}^{\pi \,}\) and O 2p electrons and is directed in the ar−br plane, i.e., perpendicular to the \({d}_{{||}}\) band. When the temperature decreases, a combination of structural distortion and electron correlation takes place, resulting in dimerization of the V atoms along the cr axis. This leads to an increased overlap of the a1g orbitals that split the \({d}_{{||}}\) band into the empty \({d}_{{||}}^{* }\) band and the populated \({d}_{{||}}\) band. The structural distortion also increases the energy of the \({\pi }^{* }\) band2. The combination of these two events opens a band gap, ultimately transforming the metallic tetragonal VO2 into a monoclinic insulator.

In recent years, strain modification has emerged as one of the most successful methods for manipulating complex oxide electronic structures25,26,27,28,29. In VO2, the MIT is modified by strain since it alters the interatomic distances; hence, the orbitals overlap, with consequences for the transition properties. The two most studied cases are those where tensile or compressive strains on the cr axis are applied through epitaxial growth of VO2 thin films by tuning the lattice mismatch as a function of the chosen substrate. Multiple studies have reported the MIT properties of VO2 films grown along the (110), (100) and (001) surfaces of TiO211,30,31,32,33,34,35. The cr axis is oriented parallel (110 and 100 orientations) or perpendicular (001 orientation) to the film surface. Since the lattice parameters of TiO2 are greater than those of VO2, compressive out-of-plane strain and in-plane tensile strain occur. In VO2 films oriented along the (110) and (100) planes, the critical temperature is higher than that in the bulk36,37, and the severe in-plane tensile strain applied to the cr axis allows the emergence of metastable phases31,38. However, for this reason, the MIT of these films is usually quite broad35,36, which hinders their potential for various applications. On the other hand, VO2 films oriented along the (001) direction experience compressive strain in the cr axis. The transition of these materials is quite sharp (which is favorable for producing devices with high ON‒OFF ratios), whereas the critical temperature is lower than that of the bulk material (as low as 295 K)33. The suppressed critical temperature may be unfavorable for devices operating at room temperature. Moreover, the high surface energy may result in undesired surface roughening, hindering the integration of these films in complex electronics39,40,41. The (001), (110) and (100) VO2 film orientations have been the most studied since they heavily strain (compressive or tensile) the cr axis.

An intermediate case is that of VO2 films grown on the TiO2 (101) surface. For this orientation, the lattice mismatch is small, resulting in a reduced strain on the cr axis that it is oriented diagonally out of plane37,41. Compared with the other cases, these films combine sharp bulk-like MITs, as in the case of films those grown along the (001) direction, with approximately room-temperature Tcs and atomically smooth surfaces, which is ideal for implementation into heterostructures34,35,41. In addition, an intermediate strain configuration is likely to minimize crack formation and self-pixelation on the film surface because the elastic stress is relieved across the MIT42,43,44, increasing the stability of the transition. However, a detailed study of the band structure of VO2 (101) as a function of strain is, to the best of our knowledge, still lacking. In particular, the effect of moderate strain on band structure anisotropy has yet to be explored.

In this framework, we investigated the role of strain as a control parameter for the band structure anisotropy of VO2 single-crystal films. Strain modulation was achieved by using VO2 thin films of 8, 16 and 32 nm thickness on TiO2 (101) substrates. The use of TiO2 (101) is relatively less studied and hence still largely unexplored, and it is expected to apply an intermediate amount of strain along the cr axis compared with that of TiO2 (001)- and (110)-oriented films34,35. The thin films set was characterized via X-ray diffraction (XRD) and resistivity measurements to determine the dependence of the film thickness on the MIT and the effect of substrate-induced strain on the lattice, respectively. The electronic structure evolution was then probed via X-ray absorption spectroscopy (XAS) and X-ray linear dichroism (XLD) at the V L3 edge and resonant photoemission spectroscopy (ResPES). These measurements were performed using linearly polarized light to maximize \({d}_{{||}}\)- and \({\pi }^{* }\)-band sensitivity. The combined use of XLD and ResPES provides a complete overview of the band-selective projections of the unoccupied and occupied density of states of VO2.

Our results revealed a progressive reduction in the anisotropy of the electronic structure of the VO2/TiO2(101) films as the thickness decreased; this is accompanied by an effective mass renormalization tending toward a scenario where \({d}_{{||}}\) and \({\pi }^{* }\) become increasingly similar as the film thickness decreases. These results highlight the key role of strain as a control parameter and the deep interconnection among band occupation, band curvature and anisotropy, which can be exploited for technological purposes.

Experimental

All the measurements were performed at 355 K except where specified otherwise. The VO2/TiO2(101) films were grown with an RF-plasma assisted oxide− molecular beam epitaxy (MBE) instrument at the University of Science and Technology of China, Hefei. The deposition chamber had a base pressure of less than 4 × 10−9 mbar. The substrate temperature was 823 K during deposition.

The synthesized thin films were characterized using XRD and resistivity measurements.

XRD measurements, both symmetric θ−2θ scans and asymmetric reciprocal space maps, were performed using a PanAnalytical X’Pert Pro diffractometer (Cu−Kα wavelength).

The TCs of the MITs for all the samples were evaluated through transport measurements using the van der Pauw method.

The spectroscopy measurements were performed at the NFFA APE-HE beamline at the Elettra synchrotron radiation facility45. XAS measurements were performed in total electron yield (TEY) mode at the V L3 edge while increasing the temperature from RT to 370 K via horizontal polarization. XLD measurements were obtained as the difference between the XAS spectra of the sample surface in different orientations with respect to the beam, as shown below. ResPES measurements were taken with a ScientaOmicron R3000 hemispherical analyzer, in which the photon energy across the V L3 edge was scanned in horizontal polarization with the sample surface normal with respect to the analyzer. The binding energies were calibrated with respect to the Fermi level of a gold reference foil.

The (101) surface of the metallic VO2 phase has [010] and [−101] vectors as in-plane lattice vectors. The ar [100] and cr [001] axes are inclined with respect to the normal to the surface with angles \(\beta \approx 58^{\circ}\) and \(\gamma \approx 32^{\circ}\) (values calculated using the data reported in JCPDS no. 76-0675). The sample surface was rotated by an angle of \(\alpha =+45^{\circ}\) or \(-45^{\circ}\) with respect to the beam to align the electric field vector of the photon beam (\(\vec{E}\)) in a parallel orientation with respect to either cr or ar (i.e., perpendicular to cr), as shown in the sketch of Fig. 1. This configuration creates an effective angle between \(\vec{E}\) and cr (ar) of \(\delta \approx 13^{\circ}\). This small angle does not significantly affect our data since both the absorption and photoemission intensities depend on \({\cos }^{2}(\delta )\)46, which in this case corresponds to ≈ \(0.95\) ensuring that the orbital polarization of our data is 95%. Polarization-dependent measurements with similar values of \(\delta\) have been successfully carried out in the literature47.

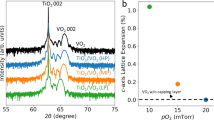
Fig. 1: Resistivity and XRD measurements of VO2(101) thin films.
figure 1

a Resistivity and XRD measurements. Schematic representation of the lattice unit cell of metallic VO2. b Top view of the polarization dependence measurements. The sample surface was rotated by an angle of ± α = 45° with respect to the incident beam direction. The angle \({\rm{\delta }}\) is the angle between the direction of the c axis and the direction of the incident beam. In the right panel, the lengths of ar and cr are equal for simplicity. c Resistivity of the three VO2/TiO2(101) films as a function of temperature. The continuous lines indicate the heating cycles, and the broken lines indicate the cooling cycles. d \({\rm{\theta }}-2{\rm{\theta }}\) scan of the 32 nm film across the phase transition. The insulating phase (indicated with M) is measured at room temperature. e (101) peak of metallic VO2 for the 8, 16 and 32 nm films. These spectra are vertically shifted for clarity. f RSM of the (301) peak for the 32 nm film in the metallic phase.

Full size image

By setting the electric field to be aligned parallel (E || cr) or perpendicular (E⊥cr, i.e., E || ar) to cr, it is possible to probe the empty \({d}_{{||}}\) and \({\pi }^{* }\) bands, respectively48.

Linear dichroism provides information on the evolution of the empty states relative to a specific band as a function of the film thickness. The XLD is calculated as follows:

$$XLD=100\times \frac{{I}_{||}-{I}_{\perp }}{{I}_{||}+{I}_{\perp }}$$
(1)

where I|| is the integrated intensity of the XAS acquired with E || cr and \({I}_{\perp }\) is that of the XAS acquired with E⊥cr. In this form, Eq. (1) can be used to determine the percentage of empty states in \({{d}}_{{||}}^{* }\) with respect to those in the \({\pi }^{* }\) band.

Results and discussion

Resistivity

The resistivity measurements as a function of temperature for the entire set of films are reported in Fig. 1c.

All the resistivity curves exhibit a variation of approximately 3 orders of magnitude across the MIT, confirming the good quality of the films for all thicknesses. The critical temperature TC (calculated as the average temperature position between the two minima of \(\frac{\partial \log \rho }{\partial T}\)) and the transition width \(\Delta\)T are reported in Table 1.

Table 1 Critical temperatures TC and transition widths ΔT as a function of the film thickness.
Full size table

The data show that the TC slightly increased by ~4 K when the film thickness was reduced. This agrees well with other studies reporting the temperature trend of VO2/TiO2(101) films41 and with what was observed for the twin VO2/TiO2(011) orientation34. On the other hand, the transition width (∆T) roughly doubles from 32 to 8 nm in thickness, indicating that strain reduces the lattice compatibility between the insulating and metallic phases of VO2/TiO2(101)49.

XRD

For all the films, the diffraction pattern shows the presence of a single-crystal phase. The \(\theta -2\theta\) scans of the 32 nm film of both the metallic and insulator phases are reported in Fig. 1d. The presence of Laue fringes indicates a sharp VO2/TiO2 interface. To calculate the ar and cr lattice parameters of metallic VO2, we measured the reciprocal space map (RSM) of the (301) peak (shown in Fig. 1f, right panel). The calculated ar and cr are 4.556 and 2.834 Ȧ, respectively. Compared with the reference value for tetragonal (metallic) VO2 reported in JCPDS no. 76-0675, we observe a shortening of the cr axis by approximately 0.7%, whereas the ar axis remains mostly unchanged. The signal from the (301) reflection of the 16 and 8 nm films was below our detection threshold; thus, we could not measure the changes in their ar and cr axes. The (101) reflection of the metallic phase for the 8, 16 and 32 nm films is shown in Fig. 1e. The increase in the full width at the half maximum of the (101) peak agrees with the reduced thickness of the films and with what has been reported in the literature41,50,51.

XAS and ResPES

To study the change in the electronic structure of metallic VO2 as a function of the film thickness, we performed XLD and ResPES measurements at the V L3 edge of the VO2/TiO2(101) films. The effect of compressive strain along cr on the band structure involves transferring part of the electron population of the \({d}_{{||}}\) band to the \({\pi }^{* }\) band2,11,30,47,52,53. This population transfer is more pronounced for thinner films since the strain increases.

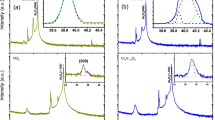
The linearly polarized XAS spectra and the calculated dichroism measured at 350 K are reported in Fig. 2a, b.

Fig. 2: XLD, resonant photoemission and mass renormalization.
figure 2

a V L3 XAS spectra for the 32 nm, 16 and 8 nm thick films (from top to bottom) at 355 K, i.e., the metallic phase. In the reported spectra, the electric field vectors of the incident photon beam were aligned parallel (red spectra) and perpendicular (blue spectra) to the cr axis, corresponding to impinging angles of α = +45 and −45, respectively (see Fig. 1). The spectra are normalized via the procedure described in ref. 47 and vertically shifted for clarity. The photon energy region where the XLD is calculated is highlighted by a black dotted box, chosen in accordance with what was reported in ref. 47, to provide the best possible frame of reference for our data. b XLD signal percentage calculated as described in Eq. (1). The broken line acts as a guide. The inset shows a sketch of the \({{\rm{d}}}_{{{||}}}-\pi\) population redistribution as a function of compressive strain and film thickness. c VB spectra at V L3 edge resonance for the metallic phase of the VO2/TiO2(101) films acquired with light polarization directed parallel and perpendicular to the cr axis. The spectra are normalized with respect to the incident photon flux and vertically shifted for clarity. d Screening length linear dichroism (in red, left axis) and effective mass linear dichroism (in black, right axis) calculated via Eqs. (4) and (5), respectively. The belts represent the uncertainty range for the points. Between the experimental points, the uncertainty value is interpolated via a polynomial function.

Full size image

Clear spectroscopic differences are observable in the XAS spectra for the two different orientations. The dichroic percentage as a function of the film thickness, calculated according to Eq. (1), is reported in Fig. 2b. The dichroic percentage decreases as the film thickness increases, a trend that is in very good agreement with similar quantifications of the \({d}_{{||}}{{-}}{\pi }^{* }\) linear dichroism47; this means that by reducing the film thickness, the empty states of d|| increase with respect to that of the \({\pi }^{* }\) band. In other words, the d|| electron population decreases as \({\pi }^{* }\) increases. These measurements demonstrate the d||−π* band population transfer for VO2/TiO2(101) films.

To investigate the effect of the population redistribution of the \({d}_{{||}}\) and \({\pi }^{* }\) bands on the electronic structure of VO2 thin films, we performed linearly polarized photoemission measurements at the V L3 edge in resonance. This technique increases the sensitivity of the bands to the photoelectron spectra and, at the same time, maximizes the photoelectron yield. In particular, when E || cr, the dipole matrix element of the V 3d photoemission spectra maximize the contribution from the \({d}_{{||}}\) orbital, whereas for E⊥cr, it maximizes the \({\pi }^{* }\) orbital54; this is particularly relevant in proximity to the FL since electron population redistribution occurs in this energy region.

We studied the VB spectra of the 8, 16, and 32 nm samples in the −2; 8 eV binding energy (BE) region collected at the maximum V L3 (518.4 ± 0.1 eV) resonance with E || cr and E⊥cr.

The spectra are reported in Fig. 2c and are in good agreement with previous ResPES measurements reported in the literature for the same compound53,55,56,57,58. Two main features are observable. The peak centered at approximately 6 eV is due to hybridization between V 3d and O 2p electrons, whereas the feature that crosses the FL is generated by unpaired 3d electrons. The L (ligand hole) and C (coherent hole) features are centered at BEs of approximately 1.7 and 0.5 eV, respectively53,56,59 for all the samples and for both orientations. The intensity of the L and C contributions changes as a function of the polarization, mirroring the band orientation in the samples. The C feature is less intense than the L feature for the 8 and 32 nm samples, whereas the opposite is true for the 16 nm sample; this may be due to surface contamination of the samples since the measurements were performed ex situ. Nonetheless, this does not influence our analysis for three main reasons: a) the photon energy is set at the VO2 V L3 resonance; therefore, the contributions from other undesired vanadium oxides (such as V2O5 or V2O3) are damped[4]; b) at 355 K, VO2 is the only metallic oxide contributing to the valence band close to the FL (except for V6O1360, which is not observed at low temperature and can thus be ruled out; and c) the orientation-dependent intensity variations of the VB at the V L3 edge are due to the orbital anisotropy of VO2 since spurious oxides are expected to contribute isotropically to the photoemission intensity.

We used linearly polarized ResPES to probe the dichroism in the metallicity (i.e., the ability to screen an electric field) induced by the change in the band population61,62,63. The maximum intensity (normalized with respect to the photon flux) of the resonant photoemission feature can be linked to the screening length via Eq. (2)61,62,63

$$\frac{I}{{I}_{0}}\propto \lambda$$
(2)

where I is the VB peak integral intensity, I0 is the incident photon flux and λ is the screening length. Owing to the orbital sensitivity of the measurements, the variation in the screening length Δλ along the cr axis and along the ar axis is calculated as follows:

$$\Delta {\lambda }_{{ca}}=100\times \frac{{I}_{c}-{I}_{a}}{{I}_{c}+{I}_{a}}\propto 100\times \frac{{\lambda }_{c}{\,-\,\lambda }_{a}}{{\lambda }_{c}{\,+\,\lambda }_{a}}$$
(3)

where \(\Delta {\lambda }_{{ca}}\) is expressed as a percentage; Ic and Ia are the normalized integrated intensities of the VB spectra acquired with E|| cr and E⊥cr, respectively; and λc and λa are the screening lengths due to the d|| and \({\pi }^{* }\) bands, respectively. To calculate \(\Delta {\lambda }_{{ca}}\), we integrated the intensity of the VB spectra in the binding energy region of 0–2 eV to include both L and C contributions. The data are represented as red dots in Fig. 2d.

\(\Delta {\lambda }_{{ca}}\) increases as the film thickness increases, indicating that the screening capability of VO2 decreases as the film thickness decreases. The anisotropy reduction also affects the effective masses of the d|| and \({\pi }^{* }\) bands. The screening length can be expressed in a general form as follows64:

$${\lambda }^{-2}=\frac{\sqrt{2}{e}^{2}{{m}^{* }}^{\frac{3}{2}}{\left({k}_{b}T\right)}^{\frac{1}{2}}}{2\pi {\varepsilon }_{0}{\hbar }^{3}}{F}_{\frac{1}{2}}^{{\prime} }\left(\frac{\mu }{{k}_{b}T}\right)$$
(4)

where e is the electron charge, \({m}^{* }\) is the effective mass, \({k}_{b}T\) is the temperature multiplied by the Boltzman constant, \(\hbar\) is the reduced Plank constant, \({\varepsilon }_{0}\) is the vacuum permeability, and \({F}_{1/2}^{{\prime} }(\mu /({k}_{b}T))\) is the first derivative of the Fermi integral of order ½ with respect to \(\mu /({k}_{b}T)\), where \(\mu\) is the chemical potential65. \({F}_{1/2}^{{\prime} }(\mu /({k}_{b}T))\) depends on the temperature and the relative position of the conduction band edge with respect to the FL.

In our case, since the polarized ResPES were acquired at the same temperature and since the chemical potential within the same sample remains the same, from Eq. (4), we obtain

$$\Delta {m}_{{ca}}^{* }=\frac{{m}_{c}^{* }{\,-\,m}_{a}^{* }}{{m}_{c}^{* }{\,+\,m}_{a}^{* }}=\frac{{\lambda }_{c}^{-\frac{4}{3}}{\,-\,\lambda }_{a}^{-\frac{4}{3}}}{{\lambda }_{c}^{-\frac{4}{3}}{\,+\,\lambda }_{a}^{-\frac{4}{3}}}$$
(5)

where \(\Delta {m}_{{ca}}^{* }\) is the difference between the effective masses \({m}_{c}^{* }\) and \({m}_{a}^{* }.\,\)The calculated \(\Delta {m}_{{ca}}^{* }\) values are reported in Fig. 2d as black squares. The trend is the same as that of \(\Delta {\lambda }_{{ca}}\), where the dichroism decreases (in absolute value) with decreasing film thickness. Our results agree well with the effective mass difference calculated via the angle-resolved photoemission data reported in66, for which \(\Delta {m}_{{ca}}^{* }\approx 18-20 \%\) for a 20 nm thick VO2 film. By reducing the film thickness, we observe an effective mass renormalization, pointing toward a reduction in the anisotropy in the band structure.

We can summarize our observations as follows: the strain-induced electronic population redistribution between \({d}_{{||}}\) and \({\pi }^{* }\) leads to increased homogeneity of the screening length and the effective mass along the ar and cr axes.

Our observations agree with the results of the LDA and DFT calculations for strained VO2 films with a shortened cr axis67,68. The reduction in the V‒V pair distance increases the overlap of the a1g (d||) orbitals, leading to renormalization of the bandwidth. This renormalization generally results in different occupation numbers in different orbitals, i.e., in charge transfer between the d|| and \({\pi }^{* }\) bands. In the case of a shortened cr axis, this results in an increase in the a1g−a1g hopping terms and an increase in the corresponding bandwidth67. This ultimately reduces the energy difference between the d|| and \({\pi }^{* }\) bands, leading to a more even population of the two bands, which weakens the repulsive electron‒electron interaction68. Our data confirm the prediction of an emerging isotropization of the band structure of VO2 films driven by strain, which acts as a parameter that control the Mott physics in multiband complex oxides.

Conclusions

The role of strain in the modulation of band structure anisotropy in metallic VO2/TiO2(101) was investigated by combining XLD and ResPES. Our single-crystal films show compressive strain along the cr axis, which leads to an electronic population redistribution between the \({d}_{{||}}\) and \({\pi }^{* }\) bands, with the two bands more evenly populated for thinner (strained) films. This leads to a decrease in the difference in screening length calculated along cr and ar as a function of film thickness, indicating a reduction in the anisotropy in the band structure of VO2. This is further confirmed by the observation of an effective mass renormalization effect, which suggests that, in addition to the redistribution between the \({d}_{{||}}\) and \({\pi }^{* }\) bands, the band curvature itself is also influenced by strain.

In other words, in the presence of interfacial strain along the (101) direction of the metallic phase, \({d}_{{||}}\) and \({\pi }^{* }\) become similar in terms of the electron population, electric field screening performance and effective mass. Strain emerges as a dominant parameter controlling the Mott physics of multiband oxides, allowing for the tuning of the anisotropy of the VO2 band structure. Our results shed light on the band structure properties of these poorly investigated strained VO2(101) thin films, whose properties are promising for technological applications based on intrinsic anisotropy of materials.