Introduction

The Dzyaloshinskii–Moriya interaction (DMI) in a ferromagnetic/nonmagnetic metal (FM/NM) multilayer plays a key role in the novel magnetic properties of spintronic applications. As an antisymmetric exchange interaction, the DMI has been described in the Fert–Levy three-site model as arising from the spin–orbit scattering of conduction electrons by nonmagnetic atoms1,2,3. In the context of multilayer systems, a disruption of the inversion symmetry at the interface of the FM/NM heterostructure leads to the emergence of an antisymmetric DMI, which is an important factor in the stabilization of non-collinear magnetic configurations such as skyrmions and the chiral domain wall4,5,6,7,8. Such a three-site model can be extended to the FM/NM/FM multilayers, where the interlayer DMI (IL-DMI) over the NM spacer layer has been observed9,10,11,12, which holds significant potential in facilitating the design of chiral spin textures13,14. The IL-DMI can also be described by the D vector. The direction of the D vector points along (MT × MB), where the MT(B) represents the magnetization of the upper (lower) layers15. Recently, the IL-DMI has also been reported to induce the field-free magnetization switching in an FM/NM multilayer16,17,18,19,20,21, presenting itself as a promising contender for the formulation of next-generation spintronic device architectures. However, the reason for the generation of IL-DMI is not yet clear. So far, the IL-DMI can only be obtained by using a special deposition condition, such as oblique sputter deposition10,17,18,19,20,22,23, or an external magnetic field during deposition11,16. The special deposition condition and the fixed direction of the IL-DMI during the sample growth process significantly affect the practical implementation and functional performance of the device. Therefore, it is crucial to elucidate the intrinsic mechanism of IL-DMI and to further control the IL-DMI.

FePt alloy with chemically ordered L10 structure with ultra-high stability is a promising candidate for next-generation spintronics, as current-induced magnetization switching (CIMS) has been widely reported21,24,25,26,27,28. In this work, we demonstrate a controllable IL-DMI in a FePt/Pt/Fe film for further investigation of CIMS. In order to clearly study the mechanism of IL-DMI formation, the FePt/Pt/Fe films were prepared without any special deposition conditions. Due to the extremely high bulk perpendicular magnetic anisotropy (PMA) of FePt, the film shows an obvious difference in the magnetic anisotropy of the two ferromagnetic layers, which is revealed by the polarized neutron reflectometry (PNR) measurements. Surprisingly, no IL-DMI is observed in the as-prepared L10-FePt/Pt/Fe film. Then, a significant IL-DMI is generated when the device is applied by a large pulsed current in a tilted magnetic field. The direction of the IL-DMI can be revised depending on the direction of the tilted magnetic field. The experimental results clearly show an interface effect on the IL-DMI, which can be confirmed by first-principles calculations. In addition, an apparent field-free magnetization switching is achieved in the L10-FePt/Pt/Fe multilayer with the controllable IL-DMI. The maximum switching ratio is observed for the device with a 1.5-nm-thick Pt spacer layer. The controllable generation of IL-DMI will pave the way for the development of practical spin–orbit torque (SOT) devices.

Results

Interlayer DMI generation

FePt(4)/Pt(t)/Fe(1) multilayers with Pt thickness ranging from 0.5 to 3 nm were deposited on the MgO(001) substrate by magnetron sputtering (see Methods). The numbers in brackets are nominal thicknesses in nanometers. The Fe50Pt50 (FePt) alloy with a chemically ordered L10 structure consists of alternate stacking of Fe and Pt atoms along the c-axis of the face-centered tetragonal (FCT) structure26,28. The details of the sample structure can be found in Supplementary Information S1, S2. To measure the IL-DMI in the FePt/Pt/Fe multilayer, the samples were fabricated into the Hall bar devices with 5 μm in width and 35 μm in length by the conventional lithography technique. Then, the angle-dependent anomalous Hall effect (AHE) loop-shift measurements with an in-plane magnetic field were carried out15,16,17 to characterize the IL-DMI. Figure 1a shows the experimental setup, where an in-plane magnetic field HIP was applied when Rxy was measured as a function of Hz. The HIP was then rotated by an azimuthal angle φ after each Rxy − Hz loop was acquired. In the FePt/Pt/Fe structure, the effective field acting on the perpendicularly magnetized FePt layer can be expressed as \({{\boldsymbol{H}}}_{z}^{{eff}}={{\boldsymbol{H}}}_{{ext}}-{\boldsymbol{D}}\times {{\boldsymbol{M}}}_{{Fe}}\) when an external magnetic field is applied along the z direction, where the Hext, D, and MFe represent external magnetic field, IL-DMI vector, and magnetic moment of Fe layer, respectively. The schematic of the external magnetic field, D vector, and IL-DMI effective field are shown in Supplementary Information S3. Thus, the AHE loop-shift \({H}_{{shift}}=\frac{{H}_{{sw}}^{D-U}+{H}_{{sw}}^{U-D}}{2}\) corresponds to the magnitude of -D × MFe, where the \({H}_{{sw}}^{D-U}\) and \({H}_{{sw}}^{U-D}\) represent the switching field of down to up and up to down. As shown in Fig. 1b, there is almost no loop shift for the as-prepared sample and the angle dependence of the AHE switching fields, \({H}_{{sw}}^{D-U}\) and \({H}_{{sw}}^{U-D}\), are similar, which indicates the absence of IL-DMI in the FePt/Pt/Fe multilayer without special deposition conditions.

Fig. 1: The generation of the D vector.
figure 1

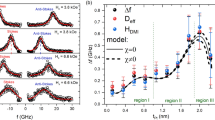
a Schematic of the loop-shift measurement. b |Hsw| as a function of φ for as-prepared FePt(4)/Pt(t)/Fe(1) film at HIP = 700 Oe. c Representative out-of-plane AHE loops at HIP = ± 700 Oe of the FePt(4)/Pt(1.5)/Fe(1) film after D-generation. Insert is the schematic of the setup for D vector generation. d |Hsw| as a function of φ for the FePt(4)/Pt(t)/Fe(1) films after D-generation under HIP = 700 Oe. e Hshift as a function of φ for the FePt(4)/Pt(t)/Fe(1) films at HIP = 700 Oe. f HDMI as a function of tPt for the FePt(4)/Pt(t)/Fe(1) films.

Full size image

To generate IL-DMI in the FePt/Pt/Fe multilayer, a postgrowth method is proposed. As shown in the inset image of Fig. 1c, first, the Hall bar device was set with a magnetic field of 2 kOe along the -x- axis. Second, the device was rotated in a clockwise direction. Here, the angle of the film apart from the x-axis, θ, is equal to 30°. Finally, a large pulsed current Ix was applied through the Hall bar along the x-axis. The further details of the IL-DMI generation will be discussed later. After the generation of IL-DMI, a large shift of the AHE loop was observed (Fig. 1c). Meanwhile, the angle dependence of the AHE switching fields, \({H}_{{sw}}^{D-U}\) and \({H}_{{sw}}^{U-D}\), show a maximum during the rotation process (Fig. 1d). When φ = 0 °, the ∣Hsw∣ is the largest, which is perpendicular to the direction of the magnetic field during the IL-DMI generation.

Figure 1e shows the angle dependence of Hshift under HIP = 700 Oe for the samples with different Pt thickness. The Hshift shows a sinusoidal variation with respect to φ and the maximum (minimum) values of the Hz shift are approximately located at φ = 180° (0°), which is perpendicular to the D vector for the FePt(4)/Pt(t)/Fe(1) multilayers with t = 1, 1.5, and 2 nm. Meanwhile, the absence of such sinusoidal dependence in the sample with tPt = 0.5 and 3 nm can be seen, indicating that the IL-DMI is suppressed due to the Pt thickness being too thin or too thick. As shown in Fig. 1f, the DMI effective field is the maximum, approximately 123 Oe, when the Pt thickness is 1.5 nm.

Figure 2 shows the detail of generating a controllable D vector in FePt/Pt/Fe multilayer. When the angle of the film apart from the x-axis, θ, is equal to 30°, the directions of two magnetizations follow the relationship of αB < αT (Fig. 2a). Here, αT(B) represents the angle for the magnetization of the upper (lower) layer apart from the normal of the film. The vector D ( = MT × MB) points into the plane. Then the device was turned 90o for the CIMS measurement, i.e., a pulsed current with a pulse width of 50 μs and an in-plane magnetic field were both along +y direction. The Hall resistance was recorded by using a small current (0.5 mA) after a delay of 6 s. As shown in Fig. 2b, there is almost no field-free magnetization switching for the as-prepared sample. Surprisingly, an obvious field-free magnetization switching can be seen in the device after the generation of IL-DMI by applying the pulse current in the tilted magnetic field. Here, the pulsed DC current for D-generation is about 20 mA with a duration of 100 μs, which is quite close to the critical current value in CIMS. For better performance, more than 10 pulses of DC current were applied. On the other hand, the directions of the two magnetizations follow the relationship of αB > αT when the device is rotated counterclockwise (θ = -30°) as shown in Fig. 2c. The D vector points out of the plane. Meanwhile, the angle dependence of the AHE switching field reverses (see Supplementary Information S4), indicating the generation of a reversed IL-DMI. Therefore, the polarity of the field-free magnetization switching is also reversed (Fig. 2d), i.e., the direction of IL-DMI can be qualitatively characterized by the field-free magnetization switching.

Fig. 2: The control of the D vector.
figure 2

a Schematic of the magnetization configuration in the FePt(4)/Pt(1.5)/Fe(1) film at θ = 30°. b Schematic of the magnetization configuration in the FePt(4)/Pt(1.5)/Fe(1) film at θ = -30°. c, d Field-free magnetization switching of the FePt(4)/Pt(1.5)/Fe(1) film before (black) and after (red) generation of D vector at θ = 30°and −30°.

Full size image

For the as-prepared FePt/Pt/Fe sample, the suppression of IL-DMI may result from the spin arrangement in the two interfaces adjacent to the Pt spacer layer. If the interfacial spins are randomly aligned, the IL-DMI should be suppressed due to the quality of the FM/NM interface. After applying a pulse current in a tilted magnetic field, the interfacial spins can be well aligned to follow their adjacent magnetization direction, resulting in the generation of the substantial IL-DMI in the FePt/Pt/Fe multilayers. Thus, the apparent field-free magnetization switching is observed.

Field-free magnetization switching

Figure 3a shows the CIMS loops of the L10-FePt(4)/Pt(1.5)/Fe(1) film under varying Hy are exemplified in, where Iy was swept from −24 to +24 mA under a static Hy ranging from −1000 to +1000 Oe. The loops exhibited opposite switching polarities under large external magnetic fields (Hy = ±1000 Oe), but the field-free magnetization switching loop has the same polarity as the positive Hy cases. The remarkable switching ratio is up to 21% in the absence of an external field, while the anomalous Hall resistance RH is obtained from AHE loops (see Supplementary Information S5). In addition, almost no switching loop was observed at Hy = -50 Oe, suggesting the existence of a large effective intrinsic field (Hin) involved in the CIMS process29,30. In Supplementary Information S6, all the CIMS curves for the L10-FePt(4)/Pt(t)/Fe(1) device are shown under the Hy range from −1000 to +1000 Oe. In particular, the Pt thickness dependence of the field-free magnetization switching loops is summarized in Fig. 3b. It is clear that field-free magnetization switching can be achieved for the devices with t = 1, 1.5, and 2 nm. Corresponding to the lack of IL-DMI, the samples with 0.5 and 3 nm Pt cannot achieve field-free magnetization switching, indicating that the performance of field-free magnetization switching is strongly related to the IL-DMI. Furthermore, the ratio of field-free magnetization switching is the highest for the device with 1.5-nm-thick Pt, while the amplitudes of HDMI and Hin are maximum (see Supplementary Information S6). In fact, the DMI field reflects the effect in the CIMS experiments where switching is absent31,32. Therefore, the relationship between the in-plane effective intrinsic field and the IL-DMI in the FePt/Pt/Fe heterostructures would require further investigation.

Fig. 3: Field-free magnetization switching of FePt(4)/Pt(t)/Fe(1) films.
figure 3

a The representative CIMS curves for the FePt(4)/Pt(1.5)/Fe(1) film. b Field-free magnetization switching of FePt(4)/Pt(t)/Fe(1) films with different Pt thickness. c The MOKE images of the field-free magnetization switching in the FePt(4)/Pt(1.5)/Fe(1) device. The numbers on the right side are the amplitudes of the pulse current in mA. Red circles mark the nucleation sites that can be repeated when negative currents are applied during a magnetization switching.

Full size image

Figure 3c shows the typical magneto-optical Kerr effect (MOKE) images for the L10-FePt(4)/Pt(1.5)/Fe(1) device to graphically illustrate the process of field-free magnetization switching (Hext = 0 Oe). The dark and bright regions correspond to the up and down magnetization states, respectively. With the increase in the amplitude of Ip, a typical magnetization reversal mode dominated by nucleation can be observed32,33,34. Note that the red circles mark the nucleation sites that can be repeated when the same positive or negative currents are applied. This means that the nucleation process after applying a large current is almost independent of the heating effect.

Polarized neutron reflectometry characterization

Figure 4a shows the out-of-plane magnetic hysteresis loops for FePt(4)/Pt(1.5)/Fe(1). The curve can be divided into two parts. The part of the approximately square loop indicates that the L10-FePt grown on MgO(001) substrate is a hard magnetic alloy with a strong PMA of HK ≈18 kOe. The slowly increasing curve with a magnetic field without hysteresis suggests that the top Fe layer is magnetically anisotropic in the plane. To further characterize the magnetic orientation of FePt and Fe layers in the FePt/Pt/Fe films, PNR measurements were performed at the Multipurpose Reflectometer beamline of the Chinese Spallation Neutron Source35,36,37. The schematic of the PNR measurement is shown in Supplementary Information S7. The neutron reflectivity curves are obtained at room temperature as the function of momentum transfer Q = 4πsinθ/λ, where λ is the neutron wavelength and θ is the incident angle between the neutron beam and the film plane. The two non-spin-flip R++ and R–– are recorded for neutrons with spins parallel or antiparallel to the applied fields (corresponding to the spin-up and spin-down neutrons, respectively). Figure 4b shows the R++ and R–– curves as a function of the perpendicular momentum transfer vector Q for the FePt(4)/Pt(1.5)/Fe(1) multilayer under an in-plane external magnetic field (Hext) of 19 kOe. The sample for the PNR measurement was capped with SiO2/Pt layers for protection. Apparently, the experimental PNR data (open circles) can be well-fitted as a simple layer model. Figure 4c shows the thickness dependence of the nuclear and magnetic scattering length densities (SLDn and SLDm). It is found that the fitted magnetization of FePt and Fe layers is 994 and 1463 emu/cm3, respectively. According to the in-plane magnetization measurement (see Supplementary Information S8), the out-of-plane magnetic anisotropy of the 4-nm-thick FePt layer is about 19 kOe, indicating that the sample can be completely saturated in the plane of the film. Therefore, we calculate that the total magnetization of the L10-FePt/Pt/Fe multilayer is about 1104 emu/cm3, which is in good agreement with the result of 1137 emu/cm3 measured by superconducting quantum interference device.

Fig. 4: PNR characterization.
figure 4

a Out-of-plane M-H curve. b PNR curves of FePt(4)/Pt(1.5)/Fe(1)/SiO2(3)/Pt(5) film at Hext = 19 kOe. c The fitted SLDn and SLDm profiles at Hext = 19 kOe. d Schematic of the magnetization in the FePt(4)/Pt(1.5)/Fe(1) film.

Full size image

If the out-of-plane component of the magnetization vector is parallel to the momentum transfer Q, it is not responsive in PNR38,39. We can calculate the title angle of the magnetization in the sample according to the in-plane component of the magnetization vector based on the PNR measurement with a small external field. In Supplementary Information S7, we show the PNR data when Hext = 1 kOe and 20 Oe. The magnetic parameters of the FePt and Fe layer are summarized in Table S1 (see Supplementary Information S7). The fitted in-plane component of magnetization for FePt and Fe layers are 285 and 1276 emu/cm3, respectively, when Hext = 1 kOe, and 143 and 1019 emu/cm3, respectively, when Hext = 20 Oe. Finally, as shown in Fig. 4d, the tilted magnetization angles for FePt and Fe layers are 16.7° and 60.7°, respectively, when Hext = 1 kOe, and 8.3° and 44.1°, respectively, when Hext = 20 Oe. Since the orientation of the out-of-plane moments returns to its initial state when the in-plane external field is reduced, the moment of FePt in the L10-FePt/Pt/Fe multilayer with 1.5-nm-thick Pt is almost perpendicular to the film plane with a tilt angle of 8.3° away from the film normal. In contrast to the FePt layer, the Fe layer growing in the direction of the MgO (001) crystal has an easy axis of 45° in the plane40,41,42. As shown by the fitting results, there is an angle of 44.1° between the magnetic moment of the Fe layer and the direction of the external magnetic field, confirming the in-plane anisotropy of the top Fe layer. Thus, an obvious difference in the magnetic anisotropy of the two ferromagnetic layers was confirmed by the polarized neutron reflectometry measurements. However, there is no IL-DMI in the L10-FePt/Pt/Fe multilayer without any special deposition condition, although the two ferromagnetic layers have very different anisotropy.

First-principles calculation

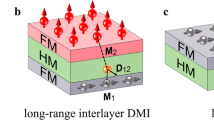
To study this interlayer DMI in our FePt/Pt/Fe system, the first-principles calculation was carried out15, in which the top Fe and bottom FePt layers are separated by NM Pt as shown in Fig. 5a. For the Fe and Pt with the face-centered cubic (FCC) structure, L10-FePt with the face-centered tetragonal, atoms are stacked in the form of ABAB… in the (001) plane. The Fe layer is shifted by (a/4, a/4, 0) (a is the lattice constant) corresponding to the 45° easy axis, which represents the case after D-generation (D-gen). For simplification, the randomly aligned interfaces for the case of as-prepared (as-pred) is achieved by removing the Fe atom layer at the Fe/Pt interface (the Red dashed circle in Fig. 5a). As shown in Fig. 5b, the component of DIL along SFe × SFePt oscillates with the angle φ resembling a simple trigonometric function, where φ is the angle between SFe and x- direction, and SFe and SFePt are the spin vectors of top Fe layer and bottom FePt layers, respectively. Evidently, the DIL reaches its maximum value when φ = 45° (Fig. 5b). Even though the value for the case of as-pred has been multiplied by five times, it is still far less than that for the case of D-gen, indicating that the IL-DMI could be greatly suppressed due to the random arrangement of interface spins.

Fig. 5: First-principles calculations of IL-DMI.
figure 5

a Side of the FePt/Pt/Fe film with the broken in-plane symmetry simulated by shifting the top Fe a/4 along the x- and y-directions. Here, a is the lattice constant. b Component of DIL along SFe × SFePt as a function of the magnetic moment orientation φ in the as-prepared and D-generated cases. SFe and SFePt are the spin vectors of the Fe and FePt layers, respectively. φ is the angle between SFe and the x-direction.

Full size image

Discussion and outlook

For the FePt/Pt/Fe films, the two ferromagnetic layers show obvious differences in HK. Therefore, the term MT × MB is not zero. According to EDM = - D · (MT × MB)9,15,17, the IL-DMI should be generated in the FM/NM/FM multilayers, which is consistent with the first-principles calculations. However, the fact that there is almost no IL-DMI in the as-prepared FePt/Pt/Fe indicates that only the difference in HK alone is not sufficient to generate the D vector. As shown in Fig. 4, the spins at the interface between FePt/Pt and Pt/Fe could be randomly aligned in the absence of any special alignment condition, such as an external magnetic field during deposition. The IL-DMI in the as-prepared FePt/Pt/Fe film could be suppressed due to the random spin arrangements at the interfaces adjacent to the Pt spacer layer. As shown in Fig. 5, the direction of the D vector is fixed when the reorientation of the interfacial spins occurs during a postgrowth method to generate the D vector. In such a postgrowth method, the device was applied by a large pulsed current in a tilted magnetic field. Thus, the interfacial spins adjacent to the Pt layer could be easily aligned along the external field due to the Joule heating by the current and the SOT effective fields23.

Similar to the well-known RKKY coupling43,44, a simple model can be used to analyze the relationship between the IL-DMI and the interfacial spins. If we assume that the effective D vector can be described as Deff = ξD0, where the D0 is the intrinsic DMI vector depending on material and interlayer thickness and the ξ is the interlayer coupling conductivity coefficient depending on the real interfaces. The IL-DMI for the as-prepared sample can be neglected due to the random distribution of interfacial spins during the layer deposition without a specific deposition condition. Therefore, ξ is close to 0. On the other hand, the realignment of interfacial spins can occur when the device is applied by a large pulsed current in a tilted magnetic field. Then a large IL-DMI with ξ ≠ 0 is generated.

Note that once the DMI vector is fixed after D-generation, the direction of the DMI vector cannot be changed even if the direction of the tilted magnetic field is revised and a higher pulsed DC is applied, which also suggests the interfacial spin structure plays a key role during the D-generation. In addition, the IL-DMI can be obtained by using a special deposition condition, such as an external magnetic field during deposition11,16. The reason may be that the interfacial spins adjacent to the spacer layer are well aligned to follow their adjacent magnetization direction during the deposition of the magnetic layers. Thus, the IL-DMI cannot be suppressed in the as-prepared multilayers.

In conclusion, we have demonstrated that an apparent field-free magnetization switching occurs in the L10-FePt/Pt/Fe films. The maximum switching ratio is observed for the device with a 1.5 nm thick Pt spacer layer. A postgrowth method has been proposed to generate the IL-DMI, although the IL-DMI is negligible for the as-prepared sample without special deposition conditions. The controllable IL-DMI arises when the device is applied by a large pulsed current in a tilted magnetic field, because the direction of the IL-DMI can be revised, depending on the direction of the tilted magnetic field. The experimental results reveal an interface effect on the IL-DMI, which is important for the applications of spin-logic devices based on the controllable generation of interlayer DMI.

Methods

Sample growth and device fabrication

The L10-Fe50Pt50 layer in Fe50Pt50(4)/Pt(t)/Fe(1)/SiO2(3) films was epitaxially deposited on the MgO(001) single-crystal substrates by using a magnetron sputtering system. The base pressure of the sputtering system was less than 5 × 10−6 Pa. The working Ar gas pressure was kept constant at 0.5 Pa. The Fe50Pt50 layers were first deposited at 450 °C, then followed by in situ annealing at 650 °C for 2 h to promote the formation of the L10 phase in the FePt alloy. After the deposition of the Fe50Pt50 single layer, the film was cooled to 150 °C and a Pt(t)/Fe(1) layer was deposited. Finally, the 3-nm-thick SiO2 layers were used as the capping layers.

Structural and magnetization characterizations

X-ray reflectivity (XRR) measurements were conducted to confirm the structural integrity, layer thickness, and interface/surface roughness of the thin films. The θ-2θ scans were performed on a high-resolution X-ray diffractometer (Panalytical MRD X’Pert 3) using Cu Kα radiation. The microstructures of Fe50Pt50(4)/Pt(t)/Fe(1)/SiO2(3) layer were characterized by a spherical-aberration-corrected FEI Themis Z microscope. The samples were prepared using Ga+ ion milling after the mechanical thinning. Both HAADF and ABF imaging were performed in the scanning mode. EDS mapping was performed at the Pt Lα and Fe Kα edges of the regions of interest. The magnetic properties were measured utilizing Superconducting quantum interference device-vibrating sample magnetometry (SQUID-VSM). All structural characterizations were performed at room temperature. Magnetic domain motion with the external magnetic field was observed by a magneto-optical Kerr effect (MOKE) technique (em-Kerr-highres).

Electrical measurements

The Hall bar devices with a width of 5 μm and a length of 35 μm were fabricated by standard photolithography combined with an argon ion etching technique. The anomalous Hall resistance and current-induced magnetization switching were measured by using a room temperature multipurpose transport measurement system with a 1 T electromagnet and a Keithley 2182 A. A Keithley 6221 was used as the source for the DC and pulsed DC measurements. For the current-induced magnetization switching and out-of-plane effective field measurements, a pulsed DC current of 50 μs duration was applied. Then the Hall resistance was recorded by using a small current (0.5 mA) after a delay of 6 s.

PNR characterization

The polarized neutron reflectometry (PNR) was carried out at the multipurpose reflectometer (MR) beamline of the Chinese Spallation Neutron Source (CSNS). Fe50Pt50(4)/Pt(t)/Fe(1)/SiO2(3)/Pt(5) was prepared on the MgO (001) substrate. The substrate size is 10 × 10 mm2. The neutron reflectivity curves are recorded at room temperature as the function of momentum transfer Q = 4πsinθ/λ, where λ is the neutron wavelength and θ is the incident angle between the neutron beam and the film plane. To access a broad momentum transfer range, reflected neutrons were collected at different incident angles. Both R++ and R–– were recorded when neutrons with spins parallel or antiparallel to the applied fields (corresponding to the spin-up and spin-down neutrons), respectively. We fitted PNR data to a model (including the layer thickness and chemical roughness) that was obtained by XRR fitting using the software GenX.

First-principles calculations of IL-DMI

All first-principles calculations within density functional theory (DFT) were implemented in the Vienna ab initio simulation package (VASP). The exchange correlation effects were calculated within the generalized gradient approximation (GGA) of Perdew–Burke–Ernzerhof (PBE) form. The cutoff energy is set to 350 eV. The G-centered 31 × 31 × 1 k-point grids are applied for sampling the Brillouin zone. Our model is FePt/Pt/Fe system as shown in Fig. 5a. In order to extract the DIL, The magnetization of the bottom FePt layer always points to z direction, while that of top Fe layer lies on the xy plane. The IL-DMI is calculated by identifying the difference between the DFT energies Ecw and Eacw for opposite-chirality spin configurations between bottom FePt and top Fe layers, which is written as: DIL = (Ecw-Eacw)/2.