Introduction

Noncollinear antiferromagnetism, often originating from magnetic competition, can manifest in various forms, including helical1,2,3, spiral4,5,6,7, chiral8,9,10,11,12, and skirmionic13,14,15 orders. Recent advancements in antiferromagnetic spintronics have enhanced the focus on noncollinear antiferromagnets16,17,18. Despite this progress, a comprehensive understanding of the complex evolution of field-driven noncollinear spin states—which are significantly influenced by magnetic anisotropy, remains elusive to date. Magnetocrystalline anisotropy (MCA), which relies on the structure and symmetry of magnetic substances, plays a critical role in stabilizing spins along preferred orientations and governs the development of anisotropic magnetic characteristics under an applied magnetic field (H)19,20.

Double helimagnetism presents a peculiar spin structure wherein two helices alternate to form a pair, resulting in noncollinear antiferromagnetism with no net moment owing to rotating spins21,22. This structure retains the benefits of antiferromagnets, such as enhanced stability without stray fields and inherently rapid spin dynamics23,24,25. However, the double-helical (DH) order is rare owing to its stringent formation conditions, necessitating nonequivalent nearest-interlayer exchange interactions that are frustrated by suitable next-interlayer interactions. Structurally, this requires magnetic layers to be separated by two distinct nonmagnetic layers stacked alternately22.

The layered kagome metal YMn6Sn6 exhibits a DH ground state as it fulfills these requirements. Kagome lattices21,26 hosting exotic field-driven noncollinear magnetic phases21,27,28 reveal nontrivial topological states and phenomena attributed to the interplay between electronic topology and magnetism21,29,30,31,32. Topological aspects such as a momentum-dependent anomalous g-factor with a broad Dirac band33, topological Hall effect in a certain magnetic phase21,28,34, and large anomalous transverse thermoelectric effect35 have been observed in YMn6Sn6. However, our current understanding of the origins of these phenomena remains limited due to the complexity of spin structures in field-induced magnetic phases.

This study proposes the DH antiferromagnetic YMn6Sn6 material as a suitable system for investigating evolving spin textures under applied and rotating H’s. By employing the frustrated Heisenberg Hamiltonian with planar magnetic anisotropy, the MCA constant is estimated to be only 0.3% of the interlayer exchange interaction, which governs overall anisotropic behavior. This approach specifically unveils an H-driven distorted conical spiral (DCS) state, distinct from previously described simple conical spirals based on neutron diffraction experiment21,27, and consistently accounts for the emergence of a fan-like (FL) state before saturation. Additionally, continuously varying spin states formed during field rotation indicate a sensitive response to MCA, which correlates with the progressive reversal trends observed in angular magnetic torques through multiple phase transitions. By understanding the intriguing interplay between the MCA and magnetic textures in YMn6Sn6, we establish a foundation for exploring magnetic topological phenomena and advancing antiferromagnetic spintronics in the realm of noncollinear antiferromagnetism.

Materials and methods

Crystal growth

Hexagonal plate-like single crystals of YMn6Sn6 were synthesized using the self-flux method29,36. Granules of Y (Alfa Aesar; 99.9%) and powders of Mn (Alfa Aesar; 99.95%) and Sn (Alfa Aesar; 99.995%) were mixed in a molar ratio of 1:1:30. The resulting mixture was transferred to an aluminum oxide crucible, sealed in a quartz tube, and heated in a tube furnace. The temperature of the furnace was gradually increased to 1000 °C over a period of 1 day and held at this value for 24 h to allow melting. The furnace was then gradually cooled to 600 °C at a rate of 5 °C/h for crystallization. Residual Sn flux on the crystal surfaces was eliminated using a stainless-steel centrifuge at 600 °C.

Magnetic properties measurements

The magnetic-field dependence of magnetization was examined using a vibrating sample magnetometer integrated into a physical property measurement system (PPMS, Quantum Design, Inc., USA). Relevant measurements were conducted under magnetic fields ranging from −9 to 9 T, applied along the a and c axes of the crystals. The magnetoresistance was measured by applying magnetic fields along the a- and c-axes in the PPMS. Magnetic torque measurements were performed using a calibrated cantilever chip (P109A, Quantum Design, Inc., USA) mounted onto a single-axis rotator in the PPMS. The torque data exhibited a low noise level of 1 × 10−9 N·m, facilitated by the use of a Wheatstone bridge circuit.

Planar anisotropic double-helical spin Hamiltonian

A DH spin model with planar magnetic anisotropy was developed to reflect the field-driven evolution of the double helix formed as a ground state in the ab plane of single-crystalline YMn6Sn6. This Hamiltonian is mathematically represented as

$${\mathcal{H}}/N={-J}_{1}\sum _{i}{\vec{S}}_{2i-1}\cdot {\vec{S}}_{2i}+{J}_{2}\sum _{i}{\vec{S}}_{2i}\cdot {\vec{S}}_{2i+1}-{J}_{3}\sum _{i}{\vec{S}}_{i}\cdot {\vec{S}}_{i+2}-g{\mu }_{B}\vec{H}\cdot \sum _{i}{\vec{S}}_{i}+K\sum _{i}{\cos }^{2}{\theta }_{i},$$

where \(N\) denotes the number of Mn moments within a single layer, \({\vec{S}}_{i}\) represents the Mn moment in the \(i\)-th layer, \(g\) = 2, and \({\mu }_{B}\) denotes the Bohr magneton. For computational convenience, the model assumes a commensurate DH spin structure of YMn6Sn6 with periodic boundary conditions. In the above expression, the first two terms represent ferromagnetic and antiferromagnetic interactions, respectively, signifying the two types of exchange couplings between neighboring layers, with \({J}_{1}\) and \({J}_{2}\) denoting the coupling strengths (\({J}_{1} > 0\) and \({J}_{2} > 0\)). The third term accounts for ferromagnetic interactions between next-nearest layers with coupling strength \({J}_{3} > 0\). The fourth term represents the Zeeman energy under a magnetic field \(\vec{H},\) which rotates from the c-axis by an angle \({\theta }_{H}\) in the ac plane, where \({\theta }_{H}=\) 0° for the c axis and \({\theta }_{H}=\) 90° for the a axis. Finally, the fifth term, \(K\sum _{i}{\cos }^{2}{\theta }_{i}\), represents the MCA energy, describing the in-plane MCA, which favors spin alignment within the easy ab plane. Here, \(K\) is the MCA constant. The angle \({\theta }_{i}\) denotes the polar angle of the net Mn moment in the \(i\)-th layer.

Results

Complex magnetic phase diagram driven by competing exchange interactions

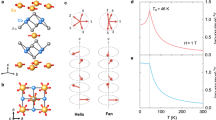
The Kagome antiferromagnet YMn6Sn6 crystallizes in a hexagonal structure (P6/mmm space group) with lattice constants of a = b = 0.552 nm and c = 0.899 nm, as derived from single-crystal X-ray diffraction data (Supplementary Fig. S1). Magnetic Mn3Sn Kagome layers, comprising corner-sharing triangles, are segregated by nonequivalent and nonmagnetic Sn3 and Sn2Y layers with distances of c1 = 0.454 nm and c2 = 0.445 nm, respectively (Fig. 1a)37. Structural details are also depicted in the scanning transmission electron microscopy images (Supplementary Fig. S2). In each layer, Mn moments are ferromagnetically coupled and confined within the ab plane owing to the planar MCA22,28. The variation in the stacking patterns of nearest layers leads to two distinct exchange interactions \({J}_{1}\) (ferromagnetic) and \({J}_{2}\) (antiferromagnetic) between adjacent magnetic layers, which are further frustrated by the next-nearest exchange interaction \({J}_{3}\) (ferromagnetic) (Fig. 1a). Despite its high degree of frustration21,27,28, YMn6Sn6 exhibits an exceptionally high Néel temperature (T) of TN = 345 K, determined by an anomaly in the magnetic susceptibility, defined as χ = M/H (Supplementary Fig. S3a). Among the interlayer interactions, \({J}_{3}\) is the weakest and decreases progressively with increasing T, attributed to thermal softening, where thermal energy disrupts the alignment of magnetic moments, weakening the exchange interaction38. The combined effects of competing interactions and minimal magnetic anisotropy create an ideal environment for exploring the evolution of noncollinear magnetic textures.

Fig. 1: Competing magnetic phases and calculated anisotropic magnetization of YMn6Sn6.
figure 1

a Crystallographic structure of YMn6Sn6, comprising a kagome network of magnetic Mn atoms in the ab plane. Mint, purple, and light gray spheres represent Y, Mn, and Sn atoms, respectively. Inequivalent neighboring exchange interactions (\({J}_{1}\) and \({J}_{2}\)) are frustrated by the next-neighboring exchange interaction (\({J}_{3}\)). Distances between layers corresponding to \({J}_{1}\), \({J}_{2}\) and \({J}_{3}\) are shown. b Magnetic phase diagram constructed from the Ha-derivative of Ma. DH, DCS, FL, and SF indicate double-helical, distorted conical-spiral, fan-like, and spin-flop phases. c Calculated isothermal magnetizations for orientations parallel to the a axis (Ma) and c axis (Mc), shown in purple and light purple solid curves, respectively, for T = 2 K (upper panel) and 250 K (lower panel), fit to the experimental data (Supplementary Fig. S3b). Purple inverted triangles corresponding to H1, H2, and H3 mark consecutive magnetic transitions. The gray dotted line is extrapolated from linear slope above H1. The orange dotted line designates the slope change of Ma at H2.

Full size image

The phase diagram constructed using the derivative of isothermal magnetization along the a axis (Ma) with respect to the applied magnetic field (Ha), dMa/dHa, reveals the complex magnetic phases within YMn6Sn6 (Fig. 1b), consistent with the findings of previous studies21,27. Our theoretical calculations identify a DH ground state stabilized by finite \({J}_{3}\), wherein the rotational (c) axis in each helix is aligned parallel to the propagation vector, kc. Upon the application of Ha, the DH state transforms into a DCS state at H1 and an FL state at H2. Eventually, Ma saturates above H3. As \({J}_{3}\) approaches zero at high T values approaching TN, the residual \({J}_{1}\) and \({J}_{2}\) components lead to a DH state with a rotating angle of 180° (\({k}_{c}=0.5\)), which doubles the unit cell along the c axis and induces a transition to the spin-flop (SF) state under the applied Ha field.

Based on a systematic analysis of the total magnetic energy, the frustrated spin model with planar MCA is fitted against experimental Ma and Mc data at T = 2 and 250 K (Supplementary Fig. S3b). The results, shown in Fig. 1c, exhibit reasonable agreement with the experimental data. However, some deviations arise in the high-field regime. Discrepancies between theoretical and experimental magnetization curves at high fields would stem from limitations of the anisotropic spin model, thermal spin fluctuations38,39, and higher-order anisotropic effects40. As strong external fields induce spin reorientation or destabilize the DH order, these factors become more pronounced41,42. However, the model still effectively captures the general magnetization trend and key features of the system’s response. Through experiments, two similar \({k}_{c}\) values are obtained, corresponding to the slightly different periodicities of the two helices21,27. For calculational convenience, T = 2 and 250 K are selected, such that the average of the \({k}_{c}\) values (0.25 and 0.3) approaches the commensurate value, with both helices sharing the same \({k}_{c}\)21. At 2 K, an abrupt increase in Ma at H1 = 2.3 T signifies transition from the DH to DCS phase, resembling SF behavior, as evidenced by the linear extrapolation above H1 intersecting at the origin, marked by the gray dotted line. A further increase in Ha reveals an additional transition from the DCS to FL phase, marked by a slope change at H2 = 6.8 T. In contrast, Mc exhibits a continuous increase through the gradual canting of Mn moments in the DH state along the Hc direction. At 250 K, similar field dependent behaviors are observed for Ma and Mc, although overall transition fields shift to lower Ha values.

Visualizing complete aspects of magnetic phases

The DH ground state is characterized by two rotation angles21,22, \(\alpha\) and \(\beta\), where \(\alpha\) denotes the relative angle of Mn moments between adjacent layers, and \(\alpha +\,\beta\) represents the relative orientation of Mn moments between two neighboring layers in a single helix (Supplementary Fig. S4). The mathematical expressions for these angles in terms of exchange interactions are given by \(\alpha =-{\cos }^{-1}[{J}_{2}{J}_{3}(\frac{1}{4{J}_{3}^{2}}-\frac{1}{{J}_{1}^{2}}+\frac{1}{{J}_{2}^{2}})]\) and \(\alpha +\beta ={\cos }^{-1}[-{\frac{1}{2}J}_{1}{J}_{2}(\frac{1}{4{J}_{3}^{2}}-\frac{1}{{J}_{1}^{2}}-\frac{1}{{J}_{2}^{2}})]\) (Section S3, Supplementary Information). At T = 2 K, the theoretical fitting with \({k}_{c}=\,\)0.25 yields exchange interaction ratios of \(\frac{{J}_{2}}{{J}_{1}}=0.364\) and \(\frac{{J}_{3}}{{J}_{1}}=0.171\), yielding \(\alpha =-{20}^{\circ }\) and \(\alpha +\beta ={90}^{\circ }\). As illustrated in Fig. 2, the \({k}_{c}=\,\)0.25 state at zero Ha comprises eight magnetic layers in a magnetic unit cell. Here, two alternating single helices are twisted by \(-{20}^{\circ }\), and spins are rotated by \({90}^{\circ }\) within each helix, propagating along the c axis. Consistency with the experimental ground-state observations of neutron diffraction studies on YMn6Sn6 is maintained by ensuring that the angles adhere to the following conditions: \(\alpha < 0\) and \(\alpha +\beta > 0\). These angles vary significantly depending on T, and \({k}_{c}\) increases with rising T27.

Fig. 2: Calculated Ha-driven magnetic phases at T = 2 K.
figure 2

Visualization of magnetic textures for DH (Ha < H1), DCS (H1 < Ha < H2), and FL (Ha > H3) states at T = 2 K. In the upper box, schematics display spin configurations at H = 0, 2.2, 4, 6, and 8 T, in which the beginnings of the arrows representing the net Mn moments in layers are placed together at one point. Each Mn layer is numbered from 1 to 8 along the c axis within a magnetic unit cell. At Ha = 0 T, the condition of propagation vector along the c axis, kc = 0.25, corresponds to the relative rotation between the two helices by an angle \(\alpha =-{20}^{\circ }\) and the spin revolution within each helix around the propagation axis by an angle \(\alpha +\beta ={90}^{\circ }\). Different colors distinguish the two alternately nested helices. Red and blue vertical dotted lines denote phase transitions, H1 and H2, respectively.

Full size image

The above fitting results in the establishment of precise spin textures evolving across different magnetic phases. At Ha = 2.2 T, the Mn moments, which initially lie close to the perpendicular direction of Ha, tend to tilt toward the Ha direction, disturbing the evenly divided angles of Mn moments within each helix. In a previous neutron diffraction experiment21, a planar Ha -driven magnetic phase appearing as a step-like jump at H1 in Ma was identified as a simple conical spiral with identical rotating modulation as the DH state, as illustrated in most previous studies21,27,43,44. A simple conical spiral distributes Mn moments at equal distances from Ha, and its rotation axis aligns with the a axis, which is perpendicular to the kc vector. However, our advanced scheme identifies this peculiar magnetic phase as the DCS, where the Mn moments rotate on the side of a distorted cone relative to the c axis, as illustrated in the spin texture at Ha = 4 T. Further application of Ha leads to the consistent closing of distorted cones in the DCS along the Ha direction, as observed in the spin configuration at Ha = 6 T. This result highlights the essential role of planar magnetic anisotropy in noncollinear antiferromagnetism. Given that the Mn moments spread sideways, the rapid suppression of the c axis component in the DCS naturally leads to the FL state, wherein the Mn moments oscillate spatially in the ab plane, propagating along the c axis across H2. A further increase in Ha saturates Ma above H3, aligning all Mn moments along the a axis. In additional calculations including \({J}_{4}\) and \({J}_{5}\)32, their contributions are found to be minor due to weaker exchange strengths (Supplementary Fig. S5), and the \({J}_{1}\)–\({J}_{3}\) model remains sufficient to capture the essential features of the DH structure and its field evolution.

Our quantification demonstrates that the exceptional feature of these magnetic textures in YMn6Sn6 stems from an extremely small MCA constant of \(K=0.003\,{J}_{1}{S}^{2}=0.038\,{\rm{meV}}\) (Supplementary Table S3). This finding, however, contradicts the intuitive notion that the MCA energy is typically comparable to the interlayer exchange coupling energy associated with a magnetic phase transition in collinearly layered antiferromagnets. In exemplary A-type antiferromagnets, a SF transition occurs at MCA constants of \(K=0.3\,{J}_{1}{S}^{2}\) and \(K=0.27\,{J}_{1}{S}^{2}\) for CaCo2As2 and MnBi2Te4, respectively, and a spin-flip transition occurs at \(K=1.4\,{J}_{1}{S}^{2}\) for Ca0.9Sr0.1Co2As245,46. Even in a single helical antiferromagnet, such as EuCo2As2, the helix-to-fan transition is observed without an intermediate DCS phase, which agrees with the strong tendency of magnetic moments to align within this plane, i.e., a large planar MCA constant of \(K=0.35\,{J}_{1}{S}^{2}=0.55\,{\rm{meV}}\)47. Consequently, the small MCA constant facilitates the exploration of the entire spectrum of magnetic phases in the double helimagnet YMn6Sn6.

At T = 250 K, the DH state with kc = 0.3 and Ha = 0 T corresponds to the characteristic angles of Mn moments, \(\alpha =-{18}^{\circ }\) and \(\alpha +\beta ={108}^{\circ }\), requiring 20 Mn-moment layers in a magnetic unit cell, as illustrated in Fig. 3. Table S3 in Supplementary Information summarizes the detailed fitting parameters. For clarity, two single helices and other phases are distinctly displayed, divided by odd and even numbers of layers. The formation of the DH state at T = 2 and 250 K can be further validated by additional theoretical calibrations for the stability of the kc = 0.5 state (Section S4, Supplementary Information). Infinitesimal perturbations to the state confirm the stable formation of the kc = 0.5 phase with \(\alpha +\beta ={180}^{\circ }\) near TN (Supplementary Fig. S6). Conversely, the estimated exchange interaction ratios at T = 2 and 250 K favor the formation of the DH phase (Supplementary Table S4). Across the step-like feature at H1 = 1.8 T for 250 K (Fig. 1c), a longer-period DCS state is formed, as indicated for Ha = 4 T. Upon increasing Ha beyond H2, further deformation along the c axis induces the FL phase in a narrow Ha interval of ~0.5 T (Fig. 1c) before reaching the saturated state at H3. Note that the narrow regime of the FL state observed in the theoretical calculations of Ma was not reflected by the Ma measurements (Supplementary Fig. S3b), attributed to thermal-fluctuation-induced smoothing at 250 K.

Fig. 3: Calculated Ha-driven magnetic phases at T = 250 K.
figure 3

Visualization of magnetic textures for DH (Ha < H1), DCS (H1 < Ha < H2), and FL (H2 < Ha < H3) states at T = 250 K. Schematics show spin configurations at H = 0, 4, and 5.5 T. Each Mn layer is numbered from 1 to 20 along the c axis within a magnetic unit cell, corresponding to kc = 0.3 (\(\alpha =-{18}^{\circ }\) and \(\alpha +\beta ={108}^{\circ }\)). Odd and even layers are shown separately to avoid complexity.

Full size image

To clarify how exchange interactions, Zeeman energy, and weak MCA collectively determine the spin texture and field-driven phase transitions, we present the evolution of these magnetic energies under Ha at T = 250 K in Fig. 4a. In zero H, this weak anisotropy imposes an easy-plane preference, ensuring the stabilization of the DH ground state by slightly favoring spin alignment within the ab plane rather than along the c-axis. Under an applied Ha, the competition between exchange interactions, Zeeman energy, and weak MCA leads to a distinctive sequence of magnetic phase transitions. In an ideal system without MCA, Ha would induce a transverse conical spiral phase, where spins uniformly tilt toward the field while maintaining their helical rotation. However, in YMn₆Sn₆, the weak MCA breaks the uniformity of spin tilting, leading instead to the DCS phase. This transition is marked by an abrupt increase in MCA energy, which reflects the emergence of a finite c-axis spin component in the DCS state (Fig. 4b). The DCS phase stabilizes because the nonuniform spins tilting to the Ha direction increases exchange energy, but this effect is compensated by a faster reduction of Zeeman energy, leading to an overall decrease in total magnetic energy. As Ha increases further, the MCA energy continues to play an important role by accelerating the suppression of the c-axis spin component. This leads to a gradual decrease in the MCA energy (Fig. 4b), driving a smooth transition into the FL phase, an intermediate state that prevents an abrupt transition from the DCS phase to full spin alignment. The reduction of MCA energy contribution during this process facilitates spin realignment within the plane. In the absence of weak MCA, YMn₆Sn₆ would likely undergo a direct transition from the DH phase (or a conventional TCS phase) to a fully aligned state, bypassing the DCS and FL phases.

Fig. 4: Magnetic field dependence of magnetic energies and large sign-changing magnetoresistanc at T = 250 K.
figure 4

a Ha-driven evolution of exchange, Zeeman and MCA energies in YMn₆Sn₆ at T = 250 K. Dotted red curves traces the minimum magnetic energy path. b Enlarged view of low-energy regime of the MCA energy. Red shaded are indicates the DCS phase. c Measured (upper panel) and estimated (lower panel) isothermal magnetoresistance, MR data, along the a-axis (MRa) and the c axis (MRc), shown in purple and light purple solid curves, respectively, for T = 250 K. Red shaded are indicates the DCS phase.

Full size image

Our approach effectively demonstrates the development of spin textures through magnetic phase transitions. However, its applicability to incommensurate kc values is hindered by the absence of appropriate boundary conditions. As detailed in Fig. S7 and Section S6 (Supplementary Information), assuming a zero MCA constant (\(K=0\)), the phase boundary between transverse conical spiral and saturated states is estimated at H3, irrespective of the commensurability of the Mn moments. Despite being a simple estimation under \(K=0\), this result aligns well with the experimental phase boundary at H3 (Fig. 1b).

A distinct spintronic feature of the DH antiferromagnet YMn₆Sn₆ is revealed through its anisotropic magnetoresistance (MR) behavior under Ha and Hc at 250 K (Fig. 4c). The MR defined as \(\frac{R\left(H\right)-R\left(0\right)}{R\left(0\right)}\) shows a notable contrast between the a- and c-axis directions (MRa and MRc), reflecting the influence of anisotropic magnetic configurations on electronic transport. Under Ha, the disruption of the balanced spin orientations in the DH ground state leads to increased scattering, resulting in a positive MRa of up to 5%. As Ha increases, MRa undergoes a sharp drop and reverses sign above the critical field H1, corresponding to the transition into the DCS phase. This sign-tunable MR, with a variation approaching 40% up to 9 T, reflects a continuous reconfiguration of spin textures, including the gradual collapse of the distorted cone structure and alignment of Mn moments with Ha. Notably, the most significant MRa variation occurs within the DCS phase. In contrast, MRc decreases monotonically with increasing Hc, consistent with continuous canting of spins along the Hc direction.

Theoretical modeling captures this anisotropic MR behavior by considering the spin-dependent conductance \(\sigma\), assumed to be proportional to the geometric average of interlayer hopping amplitudes: \(\sigma \propto {\left({\prod }_{i=1}^{20}{t}_{i,i+1}\right)}^{\frac{1}{20}}\), where \({t}_{i,{i}+1}=\,\left|\left\langle {\hat{n}}_{i},|,{\hat{n}}_{i+1}\right\rangle \right|\) denotes the overlap between spinors aligned with the net Mn moment direction in adjacent layers. Since \(R=1/\sigma\), the field-dependent MR is directly tied to the variation in these hopping amplitudes. This spintronic estimation reproduces the experimentally observed MR trends and supports the conclusion that the MR sign change is closely linked to spin texture evolution, particularly across the DH–DCS transition.

Despite the presence of highly frustrated magnetic interactions, the strong exchange interactions in YMn6Sn6 are responsible for its high Néel temperature (TN = 345 K). Specifically, the estimated intralayer and interlayer interaction energies of YMn6Sn6 (\({J}_{0}^{{eff}}{S}^{2}=31.78{\rm{meV}}\) and \({J}_{1}{S}^{2}=12.74{\rm{meV}}\)) are significantly higher than those of the single helimagnet EuCo2As2 (\({J}_{0}^{{eff}}{S}^{2}=7.18{\rm{meV}}\) and \({J}_{1}{S}^{2}=1.58{\rm{meV}}\)), which exhibits TN = 46 K (Section S5, Supplementary Information). This characteristic indicates the robustness of the magnetic order in YMn6Sn6, suggesting its potential for enhanced spintronic performance at higher temperatures. Importantly, the reversible MR sign switching observed in Ha suggests a mechanism for field-controllable resistance states, a key functionality for spin-based memory and switching devices48,49. This behavior, previously unaddressed, aligns with the phase transitions involving complex spin textures and may also be connected to topological transport phenomena, such as the topological Hall effect reported in the DCS phase21,27,28.

Intricate spin states in rotating magnetic fields, associated with angular magnetic torque

Next, angle-dependent τ was measured at T = 2 K (Supplementary Fig. S8), and the minimum total magnetic energy was calculated while systematically rotating a specific H. This allows for the representation of the explicit orientations of the net Mn moment in each layer at a given angle of H and reproduces the angular dependence of magnetic torque per unit volume, denoted as τ = M × H, as illustrated in Fig. 5. Here, θH represents the deviation of H from the c axis (θ = 0° for the c axis and θ = 90° for the a axis), and θM denotes the angle of the net M relative to θH. Thus, the magnitude of τ can be expressed as \({MH}\sin \left({\theta }_{M}-{\theta }_{H}\right)\).

Fig. 5: Measured and calculated angle dependence of magnetic torques at T = 2 K.
figure 5

a Measured (Solid dots) and calculated (Light solid curve) angular-dependent torque (τ) in the presence of rotating H = 1.8 T in the ac plane, starting from the c axis (θH = 0°). Above the graph, the angular evolution of spin textures during the rotation of H is depicted in 22.5° intervals. b, c Measured and calculated angular dependent τ and corresponding net-moment orientations in layers at H = 5.6 and 8.0 T, respectively.

Full size image

At H = 1.8 T below H1, the slope of τ at θH = 90° exceeds that at θH = 0° or 180°, indicating susceptibility to the alteration of τ near θH = 90° due to planar magnetic anisotropy (Fig. 5a). At θH = 0°, the Hc component inclines Mn moments slightly toward the c axis, forming a conical DH state. Next, by rotating H in a low θH regime, the net M in the conical DH state lags behind the H direction (θM < θH) owing to a small Ha component, resulting in a negative τ. At θH = 90°, the Mn moments are confined within the ab plane, tilting slightly toward H and producing a zero τ. Further rotation of H beyond θH = 90° leads to positive τ values because the net M is ahead of H for θH > 90°, generating a periodic angle dependence of τ. At H = 5.6 T below H2, the magnitude variation of τ with H rotation diminishes, ascribed to the suppressed overall angle difference between θH and θM (Fig. 5b). H with θH = 0° yields a conical DH state; however, the tilting angle of Mn moments is smaller than that for \(K=0\), which can be attributed to the tendency of Mn moments to lie within the ab plane. With a slight rotation of H, a large Hc component still causes the net M to rotate retardedly relative to θH, resulting in negative τ values for θM < θH. As θH increases further, the Ha component causes faster rotations of Mn moments relative to the a axis, i.e., θM > θH. The sign of τ changes to positive for θH > 45°. At θH = 90°, an Ha component exceeding H1 engenders a DCS state, in which the Mn moments are squeezed around θH = 90°, rendering τ zero. As θH crosses 90°, τ transforms from positive to negative values because the net M rotates slower relative to θH with a large Ha component for θH > 90°, causing twice as frequent sign changes. At H = 8.0 T, the overall angular dependence of τ is entirely reversed owing to an increased magnitude of τ (Fig. 5c). A conical DH state with a larger tilting angle is formed at θH = 0°. At low θH values, the larger Ha component inclines the net Mn moments closer to the a axis, resulting in a positive τ. At θH = 90°, the FL state appears as H exceeds H2. At θH > 90°, H with a negative Hc component causes the net M to turn slower than H and alters the sign of τ. The 3D contour plots of angle-dependent τ are also depicted for T = 2 and 250 K in Supplementary Figs. S9 and S10, demonstrating a distinct reversal trend of τ, closely matching experimental and theoretical outcomes.

Discussion

While a previous neutron diffraction study provided important insights into the magnetic phase diagram of YMn₆Sn₆21,27,28, it did not resolve the precise spin configurations within each phase. This limitation stems from the inherent technical challenges of detecting continuously evolving spin states in varying field conditions, especially in materials with weak MCA. In contrast, our study overcomes these challenges by employing highly sensitive angle-dependent magnetic τ measurements. These measurements enable the detection of minute τ variations arising from the anisotropic response of the spin system50, offering a powerful tool to probe subtle spin reorientations51,52. Our τ data show excellent agreement with theoretical predictions based on our easy-plane anisotropic spin model. This agreement not only validates our model but also enables a more detailed and accurate reconstruction of the spin configurations across various magnetic phases. Notably, our theoretical framework allows for the layer-resolved determination of magnetic moment orientations by minimizing the total magnetic energy, a resolution not attainable with conventional neutron diffraction techniques. These findings provide new insight into the interplay between weak MCA and field-driven spin reorientation in YMn₆Sn₆, revealing a rich and continuous evolution of spin textures that had not been previously captured.

Moreover, the results provide essential clues for the analysis of magnetic topological phenomena. The interplay between electronic topology in kagome lattices and noncollinear antiferromagnetism in YMn6Sn6 presents a fertile ground for exploring novel magnetic properties21,29,33. The recent observation of the topological Hall effect in the conical spiral phase at high temperatures suggests dynamic chiral fluctuations as a plausible explanation21. Although the scalar spin chirality is zero, magnon fluctuations can induce nonzero chiral susceptibility, contributing to the topological Hall effect. Our accurate determination of the DCS phase provides a deeper understanding of these unbalanced magnon fluctuations. It also offers fresh perspectives for scrutinizing the origin based on the Berry curvature in gapped Dirac bands associated with topologically nontrivial spin textures that are subtly influenced by planar-magnetic anisotropy.

Despite its small magnitude, the weak magnetic anisotropy plays a pivotal role in stabilizing and shaping the spin textures in YMn₆Sn₆. It not only supports the formation of the DH state by favoring in-plane spin alignment but also governs the emergence and evolution of intermediate magnetic phases under applied fields, enabling a gradual rather than abrupt transition to the field-aligned state. The anisotropic spin Hamiltonian in this study is firmly based on neutron diffraction experiment that confirmed the DH ground state of YMn₆Sn₆, and its validity is supported by good agreement with anisotropic magnetization data. Building on this experimentally established spin structure, we identify a DCS phase that naturally accounts for the emergence of the intermediate FL phase and resolves inconsistencies in earlier descriptions. By integrating experimental observations with a refined theoretical model, our work offers an improved understanding of the field-driven magnetic phase transitions and anisotropy effects in YMn₆Sn₆.