Introduction

Water dynamics on the surface of biomaterials have attracted significant attention [1, 2] because they affect protein and cell adsorption onto biomaterials [3, 4]. Additionally, water dynamics significantly influence the stability of proteins [5,6,7] and the self-assembly of biomolecules and soft matter [8,9,10], making the analysis of water dynamics around solutes an important challenge with broad implications.

Many experimental techniques have been used to investigate the water dynamics around solutes and the factors influencing them [11, 12]. Terahertz (THz) spectroscopy [13] can be used to investigate the picosecond-scale dynamics of water. Hishida et al. reported that the collective rotational dynamics of water molecules vary with the osmolyte type: protein-stabilizing and destabilizing osmolytes decelerate and accelerate water dynamics, respectively [5]. These findings suggest that the changes in water dynamics caused by osmolytes significantly influence protein stability. A THz spectroscopy-based study by Shiraga et al. indicated that trehalose, a protein-stabilizing sugar molecule, decelerates the dynamics of water molecules [14]. These studies underscore the importance of using low-molecular-weight molecules and water dynamics in stabilizing proteins. Recently, quasi-elastic neutron scattering (QENS) experiments have shown that the addition of charged lipids to zwitterionic phospholipid bilayers enhances both the translational (more than a 100 ps timescale) and rotational motions (a several picosecond timescale) of hydrated water [15]. This finding indicates that the disruption of hydrogen bonds (HBs) around charged lipid molecules likely accelerates the dynamics of the hydration water. Another study by Schiro et al. revealed that the translational motion of hydrated water on the protein surface enhances the large-scale conformational dynamics of the protein, which are essential for its function [16]. Altering the diffusion properties of water through low-molecular-weight molecules can influence protein activity. These findings suggest the importance of studying translational motions, along with rotational dynamics, to understand hydration behavior. Interestingly, many low-molecular-weight biomolecules, such as saccharides, are inherently biocompatible. According to Talon et al., the addition of glucose to water significantly decelerates water dynamics [17]. Alterations in the dynamics of water molecules caused by low-molecular-weight biomolecules may be associated with their inherent biocompatibility. Therefore, investigating the hydration states and water dynamics around low-molecular-weight molecules is important for obtaining a comprehensive understanding of protein stabilization and biocompatibility.

Introducing an osmolyte moiety into a polymer side chain results in a polymerized product (polymer) that shows a better protein stabilization effect than the osmolyte [6] and improved biocompatibility [18]. The coatings of polymer brushes formed by the polymerization of low-molecular-weight molecules show better surface coverage, thickness, and composition than low-molecular-weight molecule-terminated self-assembled monolayers (SAMs) do [19, 20]. Moreover, polymer brush-modified surfaces have significantly lower plasma protein adsorption capabilities than SAM surfaces do [21]. Notably, these polymers exhibit better biocompatibility, including improved antifouling capabilities, than low-molecular-weight molecules do, likely due to the polymeric effect. The functions of osmolytes [5] are related to their hydration structures and water dynamics around molecules; therefore, assessing the effects of polymers on water dynamics is critical for understanding protein stabilization and biocompatibility [18, 22,23,24]. Zwitterionic polymers enhance the stability of proteins without compromising their bioactivity when conjugated [25], likely owing to the incorporation of kosmotropic anions and chaotropic cations (the Hofmeister series) [26,27,28], which alter the structure of water by zwitterionic polymers. A study by Ma et al. comparing the hydration states of zwitterionic polymers with those of a typical biocompatible polymer, polyethylene glycol (PEG), using DSC [29] indicated that zwitterionic polymers exhibit greater hydration ability than does PEG. The strong hydration layers of polymers can be correlated with their antifouling performance [30]. A study by Wu et al. comparing the hydration behavior of poly(sulfobetaine methacrylate) with that of PEG using DSC and low-field nuclear magnetic resonance suggested that zwitterionic polymers have a stronger hydration ability than does PEG [31] owing to better biocompatibility. A study by Tominaga et al. analyzing water dynamics around PEG using DSC, THz, and QENS [23] reported an abundance of slow water molecules around the polymers. These studies suggest that hydration states and water dynamics critically influence protein stabilization and biocompatibility in polymers, similar to low-molecular-weight molecules. Additionally, polymerization is an effective strategy for functional amplification, and hydration states and water dynamics individually influence the functions of both low-molecular-weight molecules and polymers. However, the effects of polymerization on hydration states and water dynamics remain unclear because directly observing the detailed water states between the side chains introduced into a polymer at the molecular scale via experimental methods is challenging.

Molecular dynamics (MD) simulations can be used to investigate the dynamics of water molecules around solutes effectively at the molecular level [12, 32]. The structure of water around simple organic solutes is determined by the polarity of their functional groups and the interactions of these groups with water molecules [33]. According to Stirnemann et al., the hydrophilic functional groups in the osmolyte affect water dynamics in osmolyte solutions more strongly than the hydrophobic functional groups do [34]. These studies confirm the usefulness of MD simulations in analyzing hydration states at the molecular level. MD simulations have also been used to investigate the rotational dynamics of water molecules, which likely induce increases in the protein denaturation temperature [35]. Ab initio MD simulations suggest that the water rotation dynamics around the protein-stabilizing osmolyte trimethylamine N-oxide (TMAO) are significantly slow because of direct interactions between the negatively charged O atom of TMAO and water molecules [34, 36]. A previous study on various osmolyte solutions suggested that variations in the normalized parameter, derived by dividing the number of HBs between water molecules by the number of nearest-neighbor water molecules in the second hydration shell, affect the rotational dynamics of water [32]. Moreover, MD simulations indicate that low-molecular-weight sugar molecule (mannitol and sorbitol)-terminated SAMs show nonfouling surfaces that are resistant to nonspecific protein adsorption [37]. The tightly bound water molecules above the surface of these low-molecular-weight sugar molecules strongly repel the protein, and the water dynamics around these sugar molecules can be correlated with their biocompatibility. In addition to extensively investigating the hydration state and water dynamics around low-molecular-weight molecules, studies have focused on the water surrounding polymers. Various MD simulation studies have reported the water dynamics of biocompatible polymers [38,39,40,41]. A study by Shikata et al. investigating the hydrogen-bonding interactions between water molecules and the functional groups of polymers using MD simulations [40] suggested that the diffusion of water molecules near the polymer is linked to the breakage of HBs between the functional groups of the polymers and the interacting water molecules [39]. MD simulations indicate that PEG-conjugated proteins have better thermal stability than native proteins do [42]. Although PEG interacts with proteins by hydrophobic interactions, PEG forms many HBs with water molecules and maintains a hydration layer around the PEG‒protein conjugate. Therefore, the hydrated structure around the conjugate and interactions with proteins are essential for good protein stabilization by polymers. Although the hydration states and water dynamics around low-molecular-weight molecules and polymers have been individually assessed by MD simulations, the influence of polymerization on water dynamics at the molecular scale remains unclear.

In this study, density functional tight-binding MD (DFTB-MD) simulations were used to investigate the effects of polymerization on hydration states and water dynamics. A previous publication reported that TMAO and sn-glycero-3-phosphocholine (PC) significantly decelerate water molecules [32]. Therefore, this study focuses on the water molecules around the TMAO and PC monomers. N-[3-(Dimethylamino)propyl]acrylamide N-oxide (DMAO) and 2-methacryloyloxyethyl phosphorylcholine (MPC), which are used as monomers to convert low-molecular-weight molecules into polymers, were also investigated in this study. This paper first provides details of the MD simulations analyzed in this study, followed by a discussion of water dynamics. The dynamics of the water molecules around each osmolyte, monomer, and polymer are discussed in detail. To validate the MD simulations, their results are compared with experimental data on the amount of hydration water acquired by DSC and THz-TDS. Finally, the mechanism underlying the different trends in the rotational relaxation times of water molecules during the polymerization of DMAO and MPC is discussed.

Materials and methods

All-atom MD simulations were used to understand the mechanism of dissimilar water dynamics among osmolytes, monomers, and polymers in solution. The following systems were investigated in this study: solutions of the osmolyte TMAO, TMAO containing the monomer DMAO, poly(N-[3-(dimethylamino)propyl]acrylamide N-oxide) (PDMAO), the monomer 2-methacryloyloxyethyl phosphorylcholine (MPC), and poly(2-methacryloyloxyethyl phosphorylcholine) (PMPC). The dynamics of water molecules around low-molecular-weight PC osmolytes have been previously studied [32]. The chemical structures of the osmolytes, monomers, and polymers analyzed in this study are shown in Fig. 1a. To reduce computational costs, the polymer model was considered to comprise a single tetramer composed of four repeating monomer units. Similarly, while investigating the effect of polymerization on water dynamics, each osmolyte and monomer solution was assumed to contain four molecules. The concentration of all the solutions was 1 mol/L, and the number of water molecules in the pure water system was 216. The packmol package was used to construct models of the solutions and pure water with a density of 1.0 g/cm3 [43]; the calculated average density is shown in Table S1. Typical MD simulation snapshots are shown in Fig. 1b and S1 to illustrate the simulation setup.

Fig. 1
figure 1

a Chemical structures of the osmolyte (TMAO), monomers (DMAO and MPC), and polymers (PDMAO and PMPC). The letter n indicates the repeated number of monomer units, which is set to four for the simulations. b Typical snapshots of MD simulations for pure water and polymer–water systems

Full size image

Third-order DFTB-MD simulations using the open-source DFTB+ software (version 20.1) [44] within the NpT ensemble were used in this study along with the parameter sets 3ob [45, 46] and 3obw [47], which were carefully selected for this study. The H5 correction [48] was applied with the following specifications to precisely model the HBs in the solutions: Sr = 0.68, Sw = 0.23, kOH = 0.045, and kNH = 0.0675. A significant drawback of the DFTB calculation of water is overbinding, which leads to an incorrect estimation of the density and void formation in bulk water [49, 50]. To overcome this limitation, the 3obw parameter set was developed [47]. A previous study [51] confirmed that the radial distribution functions for water molecules are similar in the TIP4P model [52] and in DFTB with 3obw. The velocity Verlet algorithm was used to integrate the equations of motion with a time step of 1 fs. The temperature was controlled at 300 K by a Nose–Hoover thermostat [53] with a coupling strength of 3200 cm−1. The pressure of the system was isotropically controlled at 1 atm using a Berendsen barostat [54] with a damping time of 0.1 ps. Simulations were carried out under three-dimensional periodic boundary conditions. A relaxation calculation was conducted for at least 144 ps for each simulation system, followed by a production run of over 180 ps to analyze the rotational water dynamics and structure of water molecules around each osmolyte, monomer, and polymer atom. The potential energy and cell volume changes were closely monitored during the relaxation and production runs. No significant changes were observed during the production runs. The repeatability of the results was ensured by examining three trajectories of each system.

The time correlation functions of the dipole moments of the water molecules were estimated to evaluate their rotational relaxation times. First, the angle θ(t) between the dipole moment at time t and that at time t = 0 was calculated. Second, the relaxation time of each water molecule (τ) was estimated when the correlation disappeared: cos θ(t) < \({e}^{-1}\). Finally, the average relaxation time of all water molecules, 〈τ〉, was calculated. The relaxation time of the water molecules as a function of the distance from each osmolyte, monomer, or polymer atom was also analyzed. The distance between the atoms of each studied molecule and the O atoms of water in the initial state was used to analyze the rotational dynamics. The HBs between water molecules were defined on the basis of geometric criteria (Fig. S2) [55], and the water molecules donating and receiving H atoms were considered to be the donors and acceptors, respectively. The following geometric criteria were used: (i) the distance between the O atoms of the donor and acceptor is less than 3.60 Å, (ii) the distance between the H atom of the donor and the O atom of the acceptor is less than 2.45 Å, and (iii) the angle between the OH vector of the donor and the OH vector connecting the donor and acceptor is greater than 150°. Condition (i) ensures that the separation between the O atoms of the donor and acceptor is less than the first minimum of the radial distribution function, whereas conditions (ii) and (iii) are related to the orientation of the water molecules. The number of water molecules fulfilling condition (i) was counted as the number of nearest-neighbor molecules (NNN). In this study, the normalized parameter NHB/NNN was calculated by dividing the number of HBs between water molecules (NHB) by NNN.

DSC can estimate the amount of nonfreezing water, which is defined as the water that does not crystallize during DSC cycling from −100 to 50 °C. THz-TDS can estimate the amount of hydration water. In this study, hydration water refers to water molecules whose slow relaxation dynamics are absent in the THz frequency band, and the degree of reduction in the intensity of the slow relaxation mode determines the quantity of hydration water.

Results and discussion

Rotational water dynamics

DFTB-MD simulations for five zwitterionic solute solutions and pure water were used to investigate the influence of the osmolytes, monomers, and polymers in the solution on water dynamics. Tetramers of DMAO and MPC were used as polymer models (PDMAO and PMPC, respectively) to assess the effect of polymerization on rotational water dynamics. Figure 2a shows the probability density distribution of the rotational relaxation time (τ) for a pure water system, P(τ)water, which was used as a reference for analyzing the τ values of the other systems. The difference in the distributions of various systems compared with that of pure water was calculated using the formula dP = P(τ) − P(τ)water. Figure 2b shows the dP distribution for TMAO, which has negative and positive values for τ < 2.5 ps and τ > 2.5 ps, respectively. This implies that the number of fast- and slow-rotating water molecules decreases and increases, respectively, indicating that TMAO reduces the rotational speed of water molecules. DMAO, PDMAO, MPC, and PMPC show similar trends of decreasing and increasing numbers of fast- and slow-rotating water molecules, respectively, in the system (Figs. S3 and S4). Therefore, all the tested solutes reduce the rotational speed of water molecules compared with that of pure water.

Fig. 2
figure 2

Probability density distribution of the rotational relaxation time τ for pure water (P(τ)water) (a). Differences in the probability density distributions of the rotational relaxation time τ for TMAO compared with the relevant data of the pure water system (b)

Full size image

To assess the distribution differences for the monomers and polymers, the following differences in dP were analyzed: dPDMAO-PDMAO = P(τ)DMAO − P(τ)PDMAO and dPMPC-PMPC = P(τ)MPC − P(τ)PMPC, where P(τ) represents the probability density distribution of the water rotational relaxation time τ and the subscript indicates the corresponding monomer or polymer. Figure 3a,b shows the differences in the probability density distributions of the τ for the monomers and polymers. In Fig. 3a, the positive value of dP at τ < 5 ps indicates that the number of fast-rotating water molecules is greater for DMAO than for PDMAO, whereas the negative value of dP at τ > 10 ps indicates that the number of very slow-rotating water molecules increases for PDMAO (see also Fig. S5a). Figs. 3b and S5b show that compared with those for PMPC, the numbers of slow- and fast-rotating water molecules are larger and smaller, respectively, for MPC. To compare the distributions of the τ for the polymers PDMAO and PMPC, the difference in dP was analyzed using the following equation: dPPDMAO-PMPC = P(τ)PDMAO − P(τ)PMPC. Figure 3c indicates a larger number of very fast (τ < 2.5 ps) and slow-rotating (τ > 10 ps) water molecules for PDMAO than for PMPC. Moreover, the number of water molecules with intermediate relaxation times (i.e., between the very slow and fast rotational relaxation times (2.5 ps < τ < 10 ps)) is greater for PMPC than for PDMAO (Figs. 3c and S5c). Therefore, PDMAO and PMPC influence the water molecule dynamics differently.

Fig. 3
figure 3

Differences in the probability density distributions of the rotational relaxation time τ of water molecules for the following pairs of systems: (a) dPDMAO-PDMAO = P(τ)DMAO − P(τ)PDMAO, (b) dPMPC-PMPC = P(τ)MPC − P(τ)PMPC, and (c) dPPDMAO-PMPC = P(τ)PDMAO − P(τ)PMPC

Full size image

Figure 4a shows the average rotational relaxation time 〈τ〉 of water molecules for each solution. In the pure water system, where there is no interference from solutes, the 〈τ〉 of water molecules is 2.12 ps. The 〈τ〉 shows an increasing trend moving from TMAO to PDMAO and a decreasing trend moving from MPC to PMPC, which is consistent with an increase and decrease in the number of slow- and fast-rotating water molecules, respectively, in each solution. PDMAO reduces the rotational speed of water molecules more than DMAO does, whereas PMPC has the opposite effect, reducing the speed of water rotation less than MPC does.

Fig. 4
figure 4

a Average rotational relaxation time of water molecules (〈τ〉) in pure water, osmolyte/water, monomer/water, and polymer/water systems. b Relationships between the values of 〈τ〉 of all the systems analyzed in this study and the normalized parameter, NHB/NNN. NHB represents the average number of hydrogen bonds, and NNN represents the number of nearest-neighbor water molecules. The values are calculated by averaging three trajectories. The error bars represent standard deviations

Full size image

Rotational water dynamics versus the normalized parameter

To explain the origin of the rotational water dynamics in each solution, 〈τ〉 was plotted against NHB/NNN, which represents the probability of HBs forming between neighboring water molecules. This parameter is used to explain the origin of rotational water dynamics in previously published studies based on all-atom MD simulations [32, 51]. Figure 4b shows that 〈τ〉 is positively correlated with NHB/NNN. Table 1 summarizes detailed information on NHB and NNN. However, the NHB cannot explain the origin of the water rotational relaxation because there is no correlation between the NHB and water rotational relaxation values. Compared with the pure water system, the number of nearest-neighbor water molecules tends to decrease owing to the presence of solutes (osmolytes, monomers, and polymers), resulting in a high normalized value. MPC tends to reduce the rotational speed of water molecules with a high value of NHB/NNN. Although the number of nearest-neighbor water molecules decreases significantly for MPC compared with the other systems, the number of HBs between water molecules increases in MPC, resulting in a high normalized value (Table 1). The increase in hydrogen bonding between water molecules reduces the rotational speed of water molecules in MPC. Despite a similar number of HBs within water molecules in both systems, the polymer systems show a lower normalized parameter value than the monomer systems do. Compared with that in the monomer systems, the polymerization of DMAO and MPC leads to a reduction in hydrogen bonding between water molecules. Owing to increased hydrogen bonding between water molecules, the rotational water dynamics in solute/water systems are slower than those in pure water.

Table 1 Average number of hydrogen bonds (NHB), the number of nearest-neighbor water molecules (NNN), and the normalized parameter NHB/NNN for all systems
Full size table

Radial distribution functions

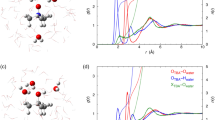
To assess the effects of interactions between solute and water molecules on the structure and rotational water dynamics around each solute, the radial distribution functions (RDFs, g(r)) of the O and H atoms of water, NHB/NNN, and τ near each osmolyte, monomer, and polymer atom were investigated. Figure 5 shows the RDFs of the O and H atoms of the water molecules, NHB/NNN, and τ around the O atoms (amino-oxide/N-oxide O atom) of TMAO, DMAO, and PDMAO. The H atom of the water molecules approaches the O atom of TMAO first (because of the partial positive charge on H), followed by the O atom of the water molecules (Fig. 5a). The first peak is observed at 2.9 Å for the O atom, indicating the presence of the first hydration shell. Another broad peak is observed for the O atom at 4.9 Å, representing the second hydration shell. The RDFs of the O and H atoms of the water molecules around the O atoms of DMAO and PDMAO show similar distributions (Fig. 5b, c). These results indicate that the amino-oxide O atoms of TMAO, DMAO, and PDMAO are well hydrated. In the first hydration shell, the value of NHB/NNN is lower than that of pure water because of the small number of nearest-neighbor molecules in water (Fig. 5d–f) and the priority of water molecule/solute interactions. However, compared with pure water, NHB/NNN increases beyond the first hydration shell, indicating the presence of an extensive hydrogen-bonding network. For TMAO, the rotational relaxation in the first hydration shell is slow because of the direct interaction between the solute and water molecules, indicating the trapping of water molecules (Fig. 5g). Compared with that of pure water, a slight increase is observed in the second hydration shell; this value remains similar to that of pure water throughout the entire range of TMAO. Interestingly, the τ in the second hydration shell is low, and the water molecules do not interact directly with TMAO. Increased hydrogen-bonding network formation beyond the first hydration shell results in slow rotational water dynamics in the system. Similar rotational relaxation is observed around the amino-oxide O atom of DMAO; however, this value is greater than that of pure water throughout this range (Fig. 5h). Therefore, the 〈τ〉 is greater for DMAO than for TMAO. For PDMAO (Fig. 5i), the rotational relaxation times of both the first and second hydration shells are greater than those of TMAO and DMAO. These results indicate that PDMAO trapped more water molecules than did TMAO and DMAO, which contributed to the higher 〈τ〉 of the PDMAO system.

Fig. 5
figure 5

RDFs of the oxygen and hydrogen atoms of water molecules around the O atom (N-oxide O atom) of (a) TMAO, (b) DMAO, and (c) PDMAO, the normalized values of NHB/NNN around the O atom of (d) TMAO, (e) DMAO, and (f) PDMAO, and the rotational relaxation time τ around the O atom of (g) TMAO, (h) DMAO, and (i) PDMAO, where r is the distance between the atoms. The dashed lines in (d–f) and (g–i) represent the corresponding values for the pure water system

Full size image

To explore the dissimilar water rotational dynamics around the carbonyl O atom in the monomer and polymer, the RDFs, NHB/NNN, and rotational relaxation times of the water molecules around the carbonyl O atom were analyzed (Fig. 6). The RDFs of the O and H atoms of water molecules and the normalized value of NHB/NNN around the carbonyl O atom of DMAO and PDMAO show a similar tendency as that observed around the amino-oxide/N-oxide O atom, indicating that the first and second hydration shells exist at 2.9 and 4.9 Å, respectively (Fig. 6a–d). Notably, compared with the DMAO system, the height of the RDFs around the carbonyl O atom is lower in the PDMAO system (Fig. 6a, b), suggesting that water molecules are less likely to be found around the carbonyl O atom of PDMAO because of the high concentration of side chains due to polymerization. The rotational relaxation at first hydration over the entire range (a flat peak within ~3.6–7 Å) is greater for PDMAO than for DMAO (Fig. 6e, f). This finding indicates that water molecules around the carbonyl O atom of PDMAO are slower or trapped more than those around the carbonyl O atom of DMAO, resulting in a greater 〈τ〉 in PDMAO.

Fig. 6
figure 6

RDFs of the oxygen and hydrogen atoms of water molecules around the O atom (carbonyl O atom) of (a) DMAO and (b) PDMAO, the normalized values of NHB/NNN around the O atom (carbonyl O atom) of (c) DMAO and (d) PDMAO, and the rotational relaxation time τ around the O atom (carbonyl O atom) of (e) DMAO and (f) PDMAO, where r is the distance between the atoms. The dashed lines in (c, d) and (e, f) represent the corresponding values of the pure water system

Full size image

To assess the water rotational dynamics around the phosphoryl group, the RDFs, NHB/NNN, and rotational relaxation time around the P atom in MPC and PMPC were analyzed (Fig. S6). RDF analysis revealed two peaks at 2.8 and ~4 Å, representing the H and O atoms of water, respectively, for both MPC and PMPC (Fig. S6a, b). The positively charged H atoms of water approach the P atoms first, followed by the O atoms of water because the negatively charged O atoms are connected to the P atom. The second peak corresponding to the water-molecule O atom is observed at ~6 Å, suggesting the existence of a second hydration shell. Although the RDFs of the water atoms and the normalized value (NHB/NNN) around the P atoms are similar for the MPC and PMPC systems (Fig. S6c, d), the water molecules in MPC are slower than those in PMPC beyond the first hydration shell (Fig. S6e, f).

To investigate the water rotational dynamics around the carbonyl O atoms of MPC and PMPC, the RDFs, NHB/NNN, and rotational relaxation time around the carbonyl O atom were analyzed (Fig. 7). Compared with those of MPC, the peak heights of the RDFs of the atoms of water molecules at 2.8 and 4 Å around the carbonyl O atom decrease for PMPC due to polymerization (Fig. 7a, b). The effect of polymerization on the probability of the presence of water molecules near the carbonyl O atom was also observed in the PDMAO system (Fig. 6a, b). Figure 7c, d shows that the NHB/NNN values for MPC and PMPC are greater than that of pure water after the first hydration shell, even beyond the second hydration shell, indicating an extensive hydrogen-bonding network in PMPC and MPC, which hinders the rotation of water molecules. Therefore, the slow rotational relaxation dynamics in the first and second hydration shells of MPC and PMPC become even slower beyond the second hydration shell, decreasing to values lower than that of pure water (Fig. 7e, f).

Fig. 7
figure 7

RDFs of the oxygen and hydrogen atoms of water molecules around the O atom (carbonyl O atom) of (a) MPC and (b) PMPC, the normalized values of NHB/NNN around the O atom (carbonyl O atom) of (c) MPC and (d) PMPC, and the rotational relaxation time τ around the O atom (carbonyl O atom) of (e) MPC and (f) PMPC, where r is the distance between the atoms. The dashed lines in (c, d) and (e, f) represent the corresponding values for the pure water system

Full size image

Comparison with the results of DSC analysis

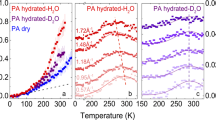
DSC analysis revealed the presence of water molecules that did not freeze because of interactions with the polymer. The DSC experiment, detailed in the Supplementary Information, can be used to estimate the maximum amount of nonfreezing water (maximum NFW) in hydrated monomers and polymers. NFW strongly interacts with solutes [4, 56]. Moreover, NFW binds strongly with polymers, resulting in the prevention of freezing, even in cycles that reduce temperatures to −100 °C [57, 58]. The direct interaction of NFW with the functional groups of the monomer and polymer retards the rotation of water molecules. The maximum NFW per monomer unit is greater in PDMAO (17.0 mol/mol) than in DMAO (11.7 mol/mol) (Table 2), which is consistent with an increase in the number of very slow-rotating water molecules in PDMAO, as predicted by MD simulations (Fig. 3a). Very slow-rotating water molecules can directly interact with the functional groups of monomers/polymers. Notably, the maximum NFW in MPC (13.6 mol/mol) is greater than that in PMPC (9.4 mol/mol) [59] owing to a reduction in the number of slow-rotating water molecules in PMPC (Fig. 3b). Although the temperature range and water content of the samples used in the DSC technique differ significantly from those used in the MD simulation conditions, the increase in NFW indicated by DSC is qualitatively consistent with the MD simulation results.

Table 2 Maximum amount of nonfreezing water (maximum NFW) per monomer unit estimated by differential scanning calorimetry
Full size table

Comparison with the results of THz-TDS

THz-TDS can detect the number of hydrated water molecules (nhyd) around a solute from changes in the water molecular dynamics on the picosecond timescale (detailed in the Supplementary Information). Hydration water includes both strongly and weakly bound water [23, 60]. For TMAO, DMAO, and PDMAO, the amount of hydration water per osmolyte/monomer unit is 7.4, 9.1, and 6.9, respectively (Table 3), and the NHB/NNN values are 0.630, 0.634, and 0.628, respectively (Table 1). The NHB/NNN values calculated by all-atom MD simulations are positively correlated (correlation coefficient, r = 0.94) with nhyd (Fig. S7), i.e., the amount of hydration water increases with increasing NHB/NNN. The same trend is observed for PMPC and MPC, which have nhyd values of 4.0 and 8.4, respectively, and NHB/NNN values of 0.628 and 0.635, respectively. Therefore, the experimental results are consistent with the simulation results, confirming their validity.

Table 3 The number of hydrated water molecules (nhyd) per monomer unit was measured by terahertz time-domain spectroscopy
Full size table

Mechanism of the influence of polymerization on water dynamics

This section discusses the mechanism of the different trends in τ for DMAO and PDMAO as well as for MPC and PMPC, which can be attributed to polymerization. As the polymerization of MPC decreases the solvent-accessible surface area (Figs. 7a, b and S8), the number of nearest-neighbor water molecules (NNN) increases in PMPC compared with that in MPC (Table 1). Although the NNN is greater in PMPC than in MPC, the number of HBs (NHB) within the water molecules remains similar in the polymer and monomer systems. The value of NHB/NNN (or the probability of forming HBs between the nearest-neighbor water molecules) is lower in PMPC than in MPC. Compared with the MPC system, the lower hydrogen-bond network formation within water molecules in PMPC significantly influences the reduction in τ in PMPC. Similarly, hydrogen-bond network formation (NHB/NNN) within water molecules in PDMAO decreases during polymerization because the NNN is greater in PDMAO than in DMAO, and the NHB values of the PDMAO and DMAO systems remain similar (Table 1). However, the 〈τ〉 of water in PDMAO tends to increase (Fig. 4a). To clarify this phenomenon, the water molecules between the side chains in PDMAO were visualized at different MD simulation times (Fig. 8 and S9) because the rotational dynamics were slower around the N-oxide O atom of PDMAO (Fig. 5i). Figure 8a shows the water molecules in the first hydration shell around the N-oxide O atom of one side chain and the carbonyl O atom of the adjacent side chain of PDMAO. One H atom of the water molecule forms an HB with the carbonyl O atom of one side chain L1, whereas the other H atom of the water molecule forms an HB with the N-oxide O atom of another side chain L2. The snapshots at different MD simulation times indicate the presence of L1 and L2 HBs (Figure 8a1–a4). Figure 8b shows the changes in the lengths of L1 and L2 with increasing MD simulation time (t); the average lengths of L1 and L2 at t values (140–167 ps) are 1.9 and 1.8 Å, respectively. Moreover, water molecules connect the N-oxide O atom and carbonyl O atom of the two side chains of PDMAO at different t values (5–30 ps), forming stable HBs (L5 and L6) (Fig. S9). Water molecules also form HBs (L3 and L4) by connecting the carbonyl O atoms of two distant side chains of PDMAO (Fig. S10). The water molecules located between the side chains in PDMAO cannot easily exchange their HBs with other water molecules for a certain period of time ( ~ 27 and 25 ps, as shown in Figs. 8, S9, respectively) and are trapped. The trapping of water molecules between the side chains increases the number of very slow-rotating water molecules in PDMAO. Consequently, the 〈τ〉 of water molecules tends to increase moving from DMAO to PDMAO.

Fig. 8
figure 8

Simulation snapshots of hydrogen bonds (HBs) between the N-oxide O atom and carbonyl O atom in two side chains of PDMAO and water molecules. a Water molecules in the first hydration shell (within 3.5 Å) of the N-oxide O atom and the carbonyl O atom in two adjacent side chains of PDMAO. Snapshots are recorded at different times (t) during MD simulation: at (a1) 137.3, (a2) 147.3, (a3) 157.3, and (a4) 167.3 ps; a water molecule connects the N-oxide O atom and carbonyl O atom by two HBs (L1 and L2). b Changes in the HB length (L) during MD simulations

Full size image

The effect of polymer chain length on hydration behavior has rarely been studied and remains a controversial and unexplored topic. Kawabe et al. suggested that the amount of hydration water can be influenced by both the length of the polymer chain and the concentration of the polymer solution: the hydration behavior strongly depends on the molecular weight at lower concentrations, whereas the hydration behavior tends to become independent of the molecular weight at higher concentrations [22]. However, the mechanisms behind these effects are not fully understood. In the present study, we used tetramers, instead of monomers, as a model for polymers at a limited computational cost. The simulation results are consistent with the experimental results. We confirmed that water molecules are trapped in the side chains, slowing the rotational dynamics of the water molecules. Although this study focused on the role of polymerization in water dynamics, the effect of the polymer chain length on hydration behavior is interesting; however, this phenomenon has yet to be elucidated and will be studied in the future.

Conclusions

In summary, this study investigates the dynamics of water molecules in solutions of the osmolyte TMAO, two monomers DMAO and MPC, and their polymers PDMAO and PMPC using DFTB-MD simulations. Compared with pure water, all the solutes reduce the rotational speed of water molecules by increasing and decreasing the number of slow- and fast-rotating water molecules, respectively. The polymerization of DMAO results in an increase in the 〈τ〉 of water molecules in the system; thus, PDMAO contains a greater number of very slow-rotating water molecules than DMAO does. A different trend is observed for MPC polymerization. PMPC decreases the number of slow-rotating water molecules in the system; polymerization decreases the solvent-accessible surface area and reduces the value of NHB/NNN. This reduction in hydrogen-bond network formation influences the reduction in τ in PMPC. However, the trapping of water molecules between the side chains of PDMAO is observed. Notably, these water molecules cannot undergo facile rotation to exchange HBs with neighboring water molecules owing to their strong HBs with side chain atoms. Therefore, PDMAO systems have a higher τ than DMAO systems owing to the trapping of water molecules or the presence of very slowly rotating water molecules. In the DSC experiments, the NFW is increased and decreased by the polymerization of DMAO and MPC, respectively, corresponding to increased and decreased trapping of water molecules. Moreover, the amount of hydration water estimated by THz-TDS strongly correlates with the values of NHB/NNN. These experimental findings confirm the validity of the MD simulation results reported in this study.

In a previous study, PDMAO enhanced protein stabilization (increased protein denaturation temperature) compared with that of low-molecular-weight osmolytes [6], likely due to the hydrated structure of PDMAO. The dynamics of hydration water or associated water can stabilize and destabilize proteins by entropic/enthalpic contributions in a crowded milieu [61, 62]. In addition, the amount of hydration water changes upon protein denaturation due to the exposure of hydrophobic groups in water and the entanglement of hydrophilic groups [63]. Changes in hydration water can strongly affect the Gibbs free energy of protein solutions [64]. THz spectroscopy indicates a strong correlation between the change in collective rotational relaxation of water and the effect of osmolytes on proteins [5]. Protein-stabilizing osmolytes tend to undergo slow water rotation. In this study, DMAO polymerization increased the τ of water, indicating that polymer-induced control of the rotational dynamics of water molecules may contribute to protein stabilization. However, the exact relationship between water dynamics and protein stabilization remains unknown. To understand the effects of water dynamics on protein stabilization, comprehensively investigating water dynamics in polymer–protein–water systems is vital.

Despite its limitations, this study contributes significantly to protein research and is expected to guide future studies on the development of high-molecular-weight polymers as protein stabilizers with high biocompatibility for application in various fields.