Introduction

Sudden cardiac death (SCD) refers to an unexpected death of cardiovascular origin in a patient suffering, or not, from an existing cardiac disorder [1]. In prospective trials, the incidence of SCD varies between 50 and 100 per 100,000 individuals. Variations in the estimations may be related to the different definitions of SCD used in the trials. Elderly subjects are particularly at risk since the incidence of SCD reaches 800 per 100,000 individuals [2].

Among the factors related to SCD, some are considered to be contributory factors and others are considered to be triggering factors [3]. The contributory factors described are: age, male sex, African origin, long QT interval, history of ischemic heart disease, heart failure, excessive alcohol consumption, sedentary life style and psychosocial factors (anxiety, depression, isolation) [4]. Other factors are considered to be triggers: mornings, Mondays, high temperatures and intense physical activity. From a pathophysiological viewpoint, intense sympathetic stimulation might be the common triggering factor [5]. In the DUKE’s predictive score of SCD, specifically established in secondary prevention in patients with documented coronary disease, seven variables that were independently linked to SCD (depressed left ventricular ejection fraction, number of diseased coronary arteries, diabetes mellitus, hypertension, heart failure, cerebrovascular disease, and tobacco use) are used [6].

Chronic kidney disease (CKD) is a well-known risk factor of cardiovascular mortality [7] and SCD in the community [8] and in populations with other pathologic conditions [9,10,11,12,13,14,15].

Serum potassium abnormalities that promote cardiac arrhythmias are also considered risk factors for sudden death [16]. Serum potassium level is controlled by renal function. In patients with CKD, serum potassium level is a factor influencing SCD even before the dialysis stage. A U-shaped curve has been described and it would appear that hypokalemia is more dangerous than hyperkalemia in renal patients [17,18,19,20,21].

Thus, the aim of our analysis was to study the combined effect of serum potassium level and renal function on the onset of SCD in elderly subjects whose renal function is often impaired and among whom there is a higher incidence of SCD. We performed a Bayesian inference analysis using a Bayesian model adjusted to the data extracted from the INdividual Data ANalysis of Antihypertensive drug intervention trials (INDANA) database, which contains the individual data of hypertensive subjects included in controlled clinical trials.

Subjects and methods

Selection of participants

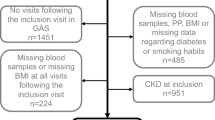
The INDANA database contains the individual data of hypertensive patients, aged 26–96 years with an average follow-up of 4.5 years [22, 23]. None of the subject was on dialysis. Of the seven studies recorded in the INDANA database, three (SHEP; n = 4736; 4.4 years of follow-up; EWPHE n = 840; 4.7 years of follow-up and COOPE n = 883; 4.5 years of follow-up) recorded baseline serum potassium and creatinine levels. The data of 3620 subjects aged 70 years or more were extracted. The COOPE study compared the effect of atenol plus bendrofluazide to control, the EWPHE study compared the effects of hydrochlorothiazide plus triamterene to placebo and the SHEP study compared the effects of chlortalidone plus atenolol or reserpine to placebo in hypertensive patients.

Variables of interest

The covariables measured at inclusion in all studies were: age, sex, smoking status (current smoker, non-smoker), BMI, history of myocardial infarction, history of stroke, history of hypertension, systolic and diastolic blood pressure, heart rate, blood glucose, cholesterolemia, creatinine level, serum potassium level and plasma uric acid. Serum potassium level was divided into three classes: hypokalemia (K < 3.5 mmol/l), normal serum potassium level (3.5 ≤ K ≤ 5.0 mmol/l), and hyperkalemia (K ≥ 5.0 mmol/l). Renal function was considered to be impaired if creatinine levels were >137 µmol/l in men and >104 µmol/l in women. These cut-off values were reported to estimate an inulin clearance of less than 60 ml/min/1.73 m²) [24]. As needed to compute probabilities for Bayesian models, continuous variables (age, BMI, systolic and diastolic blood pressure, heart rate, blood glucose, cholesterolemia, and plasma uric acid) were discretized into five classes of equal frequencies (20% of the sample).

In these studies, the definitions used for sudden death (i.e., death within 1 h of the onset of severe cardiac symptoms, unrelated to other known causes for the SHEP study) were not as precise as those recently published in the Journal of the American college of cardiology [25].

Model structure

A Bayesian network is a directed graph of a probabilistic structure. It consists of nodes and directed arrows. Each node is used to represent a variable (and its modalities), and each arrow represents a dependence between variables. Each arrow points from one “parent node” to a “child node”. The probabilistic dependencies between variables are calculated using the conditional probability as defined by Bayes’ theorem. The tree augmented naïve (TAN) algorithm was used to build the structure of the Bayesian network. The TAN algorithm uses three rules: (i) each variable is independently linked to the target variable (i.e., CV event); (ii) each variable is also linked to a unique parent node; (iii) among all possible structures, the structure that maximizes the global mutual information between variables is selected.

Thus, conditional probabilities tables are estimated using the expectation maximization algorithm. The expectation maximization algorithm is an efficient iterative procedure to compute the maximum likelihood estimation in the presence of missing or hidden data. Network learning was performed on all data files. The software used to create the model was Netica® 5.19; Norsys corporation®.

Statistics

Mean values between groups (SCD and No SCD) were compared using an analysis of variance (ANOVA) and percentages using χ2 tests.

The goodness of fit of the model was assessed using the area under the receiver operating characteristic (ROC) curve.

The mutual information of two variables measures their degree of dependence. This mutual information is null when the variables are independent, and grows when dependence increases.

Bayesian inference was performed by superimposing 100% likelihood for each of the three classes of serum potassium level and each of the two classes of renal function. The probabilities of SCD were obtained for each of the six possible combinations of serum potassium level and renal function. Comparisons of probabilities were carried out using a χ2 test. Interaction of the study treatment on SCD was also analyzed using the Bayesian network. Percentages were compared sing a χ2 test.

Statistics were performed using the MedCalc® software version 11.5.1.0.

Results

During the 4.5 years of follow-up, 81 patients (2.24%) died of SCD. Incidence rate of SCD were similar between cohorts (2.23% for SHEP, 2.0% for EWPHE, and 2.52% for COOPE).

The main characteristics of the patients who died from SCD are described in Table 1.

Table 1 Patient characteristics of patients who died from sudden cardiac death (SCD) or not (No SCD)
Full size table

Mean serum potassium and prevalence of CKD were not different in patients who died from SCD (Table 1).

The graph in Fig. 1 represents the structure of the model obtained by the TAN algorithm. Figure 2 shows the simplified model obtained using the INDANA database showing the distribution of modalities of the variables of interest (inputs: serum potassium level and renal function, and output: SCD).

Fig. 1
figure 1

Structure of the Bayesian model

Full size image
Fig. 2
figure 2

Simplified model obtained using the INDANA database showing the distribution of modalities of the variables of interest

Full size image

The area under the ROC curve of the Bayesian model for describing SCD was 0.91. In the population, the five variables that were the most linked to SCD are, in descending order: age, history of myocardial infarction, history of diabetes mellitus, serum potassium level and blood glucose (Table 2).

Table 2 Relative mutual information between SCD and variables included in the model. Age, the most linked variable, is taken as reference
Full size table

Analyses with simulated data revealed that renal failure increases the probability of SCD (2.83% vs. 2.07%; p < 0.05), that hypokalemia increases the probability of SCD (4.93% vs. 2.16%; p < 0.001) and that hyperkalemia increases the probability of SCD (2.66% vs. 2.16%; p < 0.05). Combined effects of serum potassium levels and renal function were simulated as shown in Fig. 3. Compared to the probability of SCD with normal serum potassium and normal renal function, probabilities of SCD were significantly higher in case of hypokalemia and normal renal function (4.54% vs. 2.00%; p < 0.001), hypokalemia and CKD (6.25% vs. 2.00%; p < 0.001), normal potassium level and CKD (2.73% vs. 2.00%; p < 0.05), and in case of hyperkalemia and CKD (3.35% vs. 2.00%; p < 0.001). Results are presented in Fig. 4.

Fig. 3
figure 3

Bayesian process to compute predicted probabilities of SCD in cases of various serum potassium levels and renal function

Full size image
Fig. 4
figure 4

Bayesian-estimated probabilities of sudden cardiac death (SCD) according to renal function and serum potassium level

Full size image

Study treatment did not influence the incidence of SCD that was 2.10% in the treatment group and 2.37% (NS) in the control group. In the COOPE, EWPHE and SHEP study incidences of SCD were 2.53% vs. 2.52%, 2.17% vs. 1.82% and 2.03% vs. 2.44% in the treatment and control groups, respectively.

Discussion

For a long time, serum potassium level has been known to have an effect on cardiac rhythm disorders and is considered a risk factor of SCD. Serum potassium level is controlled by renal function which is often impaired in elderly subjects. CKD is also a well-known risk factor of SCD in the community [8] and in populations with coronary artery disease [11,12,13], heart failure [9, 10, 12], end-stage renal disease [14] and in elderly [15]. The originality of our study is to have analyzed the combined effects of renal function and serum potassium in elderly hypertensive subjects.

Our analysis showed that in hypertensive subjects aged over 70 years, serum potassium level did have an effect on the risk of SCD. Hypokalemia seems to be more harmful than hyperkalemia. CKD tended to increase the risk of SCD irrespective of serum potassium levels (Fig. 4).

These results were obtained by Bayesian inference analysis of data extracted from the INDANA database [23, 24]. The INDANA contains data obtained from well-performed clinical trials. Nevertheless, only three trials in the INDANA database recorded data for baseline serum potassium and creatinine levels. Given the age of the data in the INDANA database, we did not calculate glomerular filtration rate (GFR) using a formula (Cockcroft, MDRD or CKD-EPI) to detect the presence of any CKD. CKD (GFR < 60 ml/min/1.73 m²) was estimated however using the creatinine level thresholds proposed at the time and validated using inulin renal clearances as gold standard [25]. The data being relatively old, we only used baseline data that we have linked to SCD thus eliminating the effect of treatment (which has never been found connected to SCD in the INDANA database).

The goodness of fit of the Bayesian model was confirmed by the area under the ROC curve of 0.91. We used the TAN Bayes algorithm maximizing the area under the ROC curve and confirming its relevance for modeling biomedical data [26, 27].

In comparison with a naive architecture where all the variables are considered to be independent of each other when predicting SCD, the TAN algorithm establishes relationships between variables (Fig. 1), which is much more relevant for biomedical statistics.

Our non-parametric approach using Bayesian inference is justified by the complexity of the relationships between variable modalities and the target variable: SCD. Unlike other statistical methods, Bayesian networks make no hypothesis as to the nature of the relationships between variables. Moreover, in clinical practice, the measurement of information is “noisy”, even in the best of trials, like those found in the INDANA database, even more so when the observed phenomenon is rare. Indeed, the incidence of SCD in the population of hypertensive subjects over 70 years of age in the INDANA database is low and is only 2.24% in our study.

The definition of SCD in the used studies (death within 1 h of the onset of severe cardiac symptoms, unrelated to other known causes) that is different from the recently recommended one [25] is a limitation to the interpretation of our results. The principal limitation of our study is the absence of external validation of our model. However the results of our analysis found the same main risk factors of SCD as described in the literature. The computation of mutual information on individual data is in accordance with the descriptive statistical analysis (Table 1). Even for subjects over 70 years, age remains the principal risk factor of SCD. History of myocardial infarction and of type 2 diabetes are the two other principal risk factors of SCD, as well as serum potassium level. In patients with CKD, serum potassium level is also a risk factor of SCD before the dialysis stage [20]. We found that serum potassium level affects the risk of SCD in elderly hypertensive subjects, and that hypokalemia tends to be more harmful than hyperkalemia. In the INADANA database, hypokalemia is rarely associated with renal falure and may be due to iatrogenesis (diuretics or potassium binders). CKD also exacerbated the risk of SCD, irrespective of the serum potassium levels.