Introduction

One-dimensional electronic systems provide non-trivial many-body effects that cannot be explained with single-particle pictures1. Theoretically, these effects can be calculated using bosonization techniques and the bosonic (plasmonic) scattering approach, which have been applied for both dc and ac responses even in inhomogeneous and disordered systems1,2,3,4,5,6. Experimentally, many-body states can be investigated using electronic and optical techniques7,8,9,10. Among them, one-dimensional edge channels in integer and fractional quantum Hall (QH) systems11,12,13,14 are attractive for studying non-trivial excitations in multiple channels by utilizing mesoscopic devices15,16,17,18. The focus of this study is transport eigenmodes that govern the interacting edge channels.

For example, the charge and spin (dipolar) modes for copropagating channels in the integer QH system at ν = 2 were investigated based on the Coulomb interaction in terms of the chiral Tomonaga-Luttinger liquid19,20,21. At a Y-junction where two decoupled channels join to form an interacting region, an electronic excitation incident from the non-interacting region is fractionalized into non-trivial charge and spin excitations in the interacting region19,22,23,24. In the absence of interchannel tunneling, the eigenmodes are determined by the interaction parameters and can hence deviate from the pure charge and spin modes. In this interaction-dominated regime, the fractionalization ratio assumes a non-universal interaction-dependent value, as demonstrated in frequency- and time-resolved measurements as well as noise measurements25,26,27.

A similar class of coupled modes appears when disorder allows for significant tunneling between two edge channels. A well-known example is the charge and neutral modes in the ‘hole conjugate’ fractional QH state at ν = 2/3, as suggested by noise measurements and transport properties for short interacting regions28,29,30,31,32,33. We assumed a reconstructed edge with counterpropagating integer and fractional channels12,13, whereas alternative effective models can be considered34,35. Theoretically, the charge and neutral modes appear at the Kane-Fisher-Polchinski fixed point in the renormalization group flow36. In this disorder-dominated regime, an elementary excitation should be fractionalized into pure charge and neutral modes with a quantized ratio at a Y junction of interacting and non-interacting regions36,37.

In this study, we have experimentally identified this quantized fractionalization ratio by employing time-resolved measurements for the hole-conjugate fractional state at ν = 2/3. A similar quantized fractionalization is also found in the integer QH state at ν = 2 in the presence of significant tunneling. The obtained feature is supported by a simulation involving a realistic model based on the plasmon scattering approach. The quantized charge fractionalization describes the dc characteristics as well.

Results

Fractionalization processes

We first consider the edge of the fractional state at ν = 2/3, where the counterpropagating Δν = 1 and 1/3 one-dimensional channels12 are formed along the interface to the electronic vacuum (ν = 0), as shown in Fig. 1a. Here, Δν = |ν1 − ν2| denotes a channel along an interface between insulating (incompressible) regions with ν = ν1 and ν2. Disorder-induced scattering renders them describable as a composite Δν = 2/3 channel with two counterpropagating transport modes36, i.e., a charge mode carrying a charge and a neutral mode carrying heat. We address fractionalization processes at Y-junctions comprising Δν = 1, 2/3, and 1/3 channels, as shown in Fig. 1b–d. Two types of Y-junctions are possible, i.e., YC and YN, which form depending on the cyclic order of the insulating regions and the direction of the magnetic field B. For the configuration shown in Fig. 1b, a wave packet of charge q incident from the Δν = 1 channel is fractionalized with factor r (= 1/3 in the disorder dominated regime) at junction YC into fractional charges (1−r)q and rq, which propagate through the Δν = 2/3 and Δν = 1/3 channels, respectively. This occurs because the charge mode in the Δν = 2/3 channel is composed of charges q in the Δν = 1 channel and −rq in the Δν = 1/3 channel36. The formation of this collective excitation requires a charge rq to be reflected back into the uncoupled Δν = 1/3 channel37. A similar reflection is expected when a wave packet of charge q is injected from a Δν = 1/3 channel to junction YN shown in Fig. 1c, where neutral excitation in the Δν = 2/3 channel is formed by reflecting charge q in the downstream Δν = 1 channel. As shown in Fig. 1d, a charge wave packet in the charge mode of the Δν = 2/3 channel is decomposed into a charge in the Δν = 1 channel and heat in the neutral mode. We focus on the charge fractionalization by neglecting neutral excitations as the length of the Δν = 2/3 channel (L > 100 μm) is much longer than the equilibration length leq (typically ~ 10 μm)32,33.

Fig. 1: QH Y-junctions formed with Δν = 1, 2/3, and 1/3 channels.
figure 1

a The charge and neutral modes in the disorder dominated regime of a composite Δν = 2/3 channel comprising Δν = 1 (blue) and 1/3 (red) channels along the boundaries of a hole-conjugate QH region with ν = 2/3, a narrow integer state with ν = 1, and the electronic vacuum (ν = 0). Excitations are represented by positive and negative wave packets with ratios of charges in Δν = 1 and 1/3 channels (1:−1/3 for the charge mode and 1:−1 for the neutral mode). b Charge fractionalization at junction YC. An incoming wave packet with charge q in the Δν = 1 channel is fractionalized into two packets with 2q/3 (comprising q and −q/3) in the Δν = 2/3 channel and q/3 in the Δν = 1/3 channel. c, d Neutral reflections at junction YN. An injected packet with charge q in the Δν = 1/3 channel splits into charge q in the Δν = 1 channel and neutral excitation (comprising −q and q) in the Δν = 2/3 channel in c, and so as the packet in the Δν = 2/3 channel in d.

Full size image

Quantized fractionalization in ν = 2/3 case

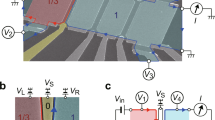
We demonstrate the charge fractionalization in time-domain measurements using several devices formed in a standard AlGaAs/GaAs heterostructure (see Methods and Supplementary Note 1). The following data were obtained at ~50 mK from devices #1 and #2 fabricated on the same chip, as schematically shown in Fig. 2a. For device #1, two Y-junctions, YC and YN, formed at the intersections of the three regions—the ungated region with bulk filling factor νB = 2/3, the gated region with a tunable νG (=1 in Fig. 2a), and vacuum. An initial charge wave packet was excited by applying a voltage step to the injector gate GI, and the waveforms of the charge packets after passing through the junctions were investigated by applying a voltage pulse of width tw (0.08-0.15 ns) to the detector gate GD. Charge waveforms were obtained by measuring the detector current ID at various time delays td of the voltage pulse with respect to the voltage step (see Methods)38. Trace (i) in Fig. 2b is a reference showing that a single charge packet was observed for νG = 0 (the gate voltage Vg = −0.3 V), i.e., when a single Δν = 2/3 channel without Y-junctions is formed, as shown in the inset. This is a typical characteristic of the edge magnetoplasmon mode39,40,41 at ν = 2/3. When the YC and YN junctions were activated by setting νG = 1 (Vg = +0.26 V, B = 11.5 T), a clear charge fractionalization manifested as two distinct packets in trace (ii). The first packet is associated with the direct propagation through junction YN, Δν = 1 channel, and junction YC. The second one is delayed by the round trip around the gated region, as illustrated in the insets. Subsequent packets associated with further fractionalization processes are extremely small to be resolved. By assuming r = 1/3, the entire process yields a series of packets with 2q/3, 2q/9, … toward the detector. We evaluated the charge qt in the reference wave packet in (i) as well as qf1 and qf2 in the first and second packets in (ii), respectively, from the area of the peaks. The obtained qt, qf1, and qf2 are plotted in Fig. 3b as a function of Vg, with the vertical axis normalized by the qt value at Vg = −0.3 V (νG = 0). The ratios qf1/qt and qf2/qt are similar to the expected values of (1−r) = 2/3 and (1−r)r = 2/9, respectively, when the Δν = 1 and 1/3 channels are well defined at νG ≥ 1. In particular, r = qf2/qf1 estimated from each ID profile yields r = 0.34 ± 0.03 in the range of Vg = 0.21-0.27 V, as shown in the inset of Fig. 3b, consistent with the quantized value of 1/3.

Fig. 2: Quantized fractionalization of charge wave packets.
figure 2

a Measurement setup with devices #1 and #2. Application of voltage Vg to the large gate (yellow) forms a rectangular QH region (L = 300 μm and ℓ = 20 μm for #1) and QH junctions YN and YC at νG = 1 and νB = 2/3. For #1, an initial wave packet is excited by applying a voltage step to the injector gate GI with the underneath fully depleted. Fractionalized wave packets are detected by applying a voltage pulse of width tw to transmit a part of the packet to be detected as current ID. For #2, two-terminal dc conductance G through similar Y-junctions is measured with ohmic contacts in Corbino geometry. b Typical charge waveforms obtained in current ID as a function of delay time td of the detector voltage pulse with respect to the excitation voltage step. The reference trace (i) at νG = 0 (Vg = −0.3 V) and trace (ii) showing charge fractionalizations at νG = 1 (Vg = 0.26 V) were obtained at νB = 2/3 (B = 11.5 T). Areas under the peaks represent charges with ratios qf1/qt ~ 2/3 and qf2/qf1 ~ 2/9. c The reference trace (i) at νG = 0 (Vg = −0.3 V) and trace (ii) showing fractionalizations at νG = 2 (Vg = 0.34 V) obtained at νB = 1 (B = 7.5 T). The areas under the peaks show qf2/qf1 ~ 1/2 and qf3/qt ~ 1/4. Propagation of charge wave packets is illustrated in the respective insets.

Full size image
Fig. 3: Characteristics of charge transport.
figure 3

a, d Vg-dependence of two-terminal conductance G measured with ohmic contacts Ω1 and Ω2 of device #2 obtained at νB = 2/3 in a and νB = 1 in d. The insets show the channel configurations, where multiple charge fractionalizations at Y-junctions explain the plateau G = e2/6 h at νG = 1 in a and G = e2/3 h at νG = 2 in d. b, e The reference charge qt, and fractionalized charges qf1, qf2, and qf3 in the respective packets normalized by qt. A single reference packet typically involves qt \(\cong\) 240e in b and 30e in e. The clear plateaus of qf/qt indicate the quantized fractionalization. The insets show fractionalization factor r = qf2/qf1 with a constant region (r = 0.34 ± 0.03 in b and r = 0.49 ± 0.03 in e). c, f Charge velocities of the channels. The Δν = 1/3 interface channel between ν = 1 and 2/3 regions, the Δν = 1 edge channel between νG = 1 and vacuum, and the Δν = 2/3 composite channel between νG = 0 and νB = 2/3 are shown in c, whereas the Δν = 1 interface channel between νG = 2 and νB = 1 regions (0.3 V < Vg < 0.4 V, estimated from the second and the third packets), the Δν = 1 edge channel between νG = 1 and vacuum (Vg < 0.18 V), and the Δν = 2 composite channel between νG = 2 and vacuum are shown in f. Data in b, c, e, and f were obtained using device #1. Vertical dotted lines for representative νG values were determined from a separate four-terminal measurement (see Supplementary Note 1).

Full size image

This observation is supported by the dc characteristics of device #2, which has Corbino geometry with ohmic contacts surrounded by a QH state, as shown in the lower part of Fig. 2a. Transport through the Δν = 1/3 channel formed between νG = 1 and νB = 2/3 regions involves the equilibration associated with scattering between the coupled Δν = 1 and 1/3 channels inside the composite Δν = 2/3 channels. Fig. 3a shows the two-terminal conductance G between ohmic contacts Ω1 and Ω2 with other ohmic contacts floating. The clear plateau of G ≅ e2/6 h at Vg ~ +0.2 V (νG = 1) ensures a full equilibration in the Δν = 1/3 channel and negligible backscattering in both νG = 1 and νB = 2/3 regions. This is a requisite for clear quantization of r = 1/3. Whereas the dc characteristics of systems involving composite Δν = 2/3 channels have been successfully explained in various ways32,33,37, we herein demonstrate that the same can also be understood with the quantized charge fractionalization. As shown by the simplified channel configuration in the inset of Fig. 3a, a fictitious charge packet q emanating from Ω1 is fractionalized into a series of charge packets through the paths shown by the dashed lines. Some of them reach Ω2 with the first charge 2q/9 through path Ω1 - YN - YC’ - YN’ - YC - Ω2, followed by others multiplied by the geometric ratio of 1/9 associated with round trip YC - YN - YC’ - YN’ - YC. The total charge q/4 reaching Ω2 explains G = e2/6 h for the conductance 2e2/3 h of the source channels connected to Ω1 and Ω2. Hence, charge fractionalization provides a unified view of dc and time-dependent charge transport.

Quantized fractionalization in ν = 2 case

We observed similar quantized fractionalization with integer QH states at νG = 2 and νB = 1, when the two Δν = 1 channels with up- and down-spins were prepared in the disorder-dominated regime. The two channels are coupled to form a composite Δν = 2 channel, as shown in the bottom inset of Fig. 2c. Significant scattering between them is allowed for example by coupling to nuclear spins42. Separate experiments show full equilibration for a channel length of ~300 μm in device #2 (see Supplementary Note 2). Our previous study showed a short equilibration length of ~10 μm in a similar device with a slightly lower electron density33. In this disorder-dominated regime, the transport eigenmodes of the Δν = 2 channel should be a pure symmetric charge mode and a short-lived antisymmetric neutral mode (see Methods). These modes are excited at junction YE and decomposed at junction YD with quantized charge fractionalization of factor r = 1/2. Namely, a single charge packet with q in the symmetric mode splits into two packets with (1−r)q and rq in the up- and down-spin channels, respectively. Compared with the reference trace (i) in Fig. 2c for (νG, νB) = (0, 1), trace (ii) shows charge fractionalizations for (νG, νB) = (2, 1) at Vg = +0.34 V and B = 7.5 T. A series of well-isolated packets, qf1, qf2, …, manifests the multiple fractionalization processes at YD. As plotted in Fig. 3e, the fractionalization factor r = qf1/qf2 = 0.49 ± 0.03 obtained in the range of Vg = 0.31-0.37 V is consistent with the quantized value of 1/2. This is in contrast to previous studies pertaining to the interaction dominated regime, where asymmetric modes with an interaction dependent factor of r ~ 0.4 were observed26,27.

We observed a clear two-terminal conductance plateau G = e2/3 h at (νG, νB) = (2, 1) using device #2, as shown in Fig. 3d. This conductance is 1/3 of the original G = e2/h of the single integer channel emanating from the ohmic contacts. This can be understood as the sum of the first transmission coefficient (the square of the fractionalization factor 1/2) of a fictitious charge packet through path Ω1 - YE - YD’ - YE’ - YD - Ω2 followed by others with a geometric ratio of 1/4 associated with round trip YD - YE - YD’ - YE’ - YD, as shown in the inset. Hence, the quantized fractionalization also explains the dc characteristics of the integer channels.

Plasmon velocities

The velocity of the wave packet is an important parameter that reflects the interaction, as evident from chiral Tomonaga-Luttinger theories2,10,19. We experimentally estimated the velocities from the time of flight, as summarized in Fig. 3c, f. The velocities of the edge channels (Δν = 1 channel between νG = 1 and vacuum and Δν = 2/3 channel between νG = 0 and νB = 2/3 in Fig. 3c) are comparable to those in previous reports regarding edge magnetoplasmons38,39,43,44. The velocity of the Δν = 1/3 interface channel between the ν = 1 and 2/3 regions, ~30 km/s, is particularly important for transporting fractional charges45. Unlike edge channels with a well-defined confining potential, the interface channel is supported by two QH states with a slight difference in their electrostatic potentials. Therefore, the contribution of the single-particle drift velocity arising from the potential gradient is negligible. This is particularly relevant to the Δν = 1/3 channel, as the Fermi level remains in the lowest Landau level in the fractional state.

To understand the origin of the velocity, we assume that the charge velocity of a Δν channel is expressed as vc = Δνgq/C, where gq = e2/h is the quantized conductance, and 1/C measures the interaction16. Practically, C should be dominated by the geometric capacitance (per unit length) between the channel and a nearby gate46. For an interface channel along the side of the gate shown in Fig. 4a, this C is expected to depend on the width, w = wg + wu, of the channel (compressible region), where wg (wu) is the spread under the gate (in the ungated region). Our numerical simulation (see Methods) shows that C is determined primarily by wg rather than wu (Fig. 4b). The normalized velocities, vc/Δν, obtained for various values of (νG, νB), are summarized in Fig. 4d. Here, the data for νG > νB and νG < νB were obtained using devices #1 and #2, respectively, with Vg > 0 and Vg < 0 (see Supplementary Notes 2 and 3). Except for (νG, νB) = (2/3, 1), vc/Δν indicates similar values for all interface channels, i.e. Δν = 1/3 (circles) and 1 (squares), as well as edge channel Δν = 1 (triangles). This coincidence suggests that the velocities are determined by a similar C ~ 0.4 nF/m, as shown on the right axis. A comparison with Fig. 4b implies that wg is sufficiently narrow, comparable to the depth d ~ 100 nm of the electron system from the surface. This indicates that the velocity ~30 km/s of the Δν = 1/3 channel obtained for (νG, νB) = (1, 2/3) is reasonable. Meanwhile, a significantly lower velocity of ~ 1 km/s was observed for the Δν = 1/3 channels in the (2/3, 1) configuration. This suggests a wide wg ~ 10 μm in the crude model or quasi-diffusive transport in the presence of disorder potential. Whereas this might be related to the small energy gaps of the QH states at lower B in this configuration, the velocity did not increase significantly with B even after light irradiation (solid circle), which increased the electron density. The former (1, 2/3) configuration with a fractional state in an ungated region might be suitable for minimizing the time-of-flight and hence decoherence in a fractional-charge interferometer. It is noteworthy that the fractionalization factor r summarized in Fig. 4c remained at approximately 1/3 even when the velocity reduced significantly.

Fig. 4: Velocity of the interface mode.
figure 4

a Schematic cross-section around the interface channel Δν = |ν1 − ν2 | of width wg + wu (wg in the gated region and wu in the ungated region) between two QH states at ν1 and ν2. The interaction inside the channel can be described with geometric capacitance C to the gate. b Calculated capacitance C as a function of wg for several wu values. c Fractionalization factor r for junction YC obtained at (νG, νB) = (2/3, 1) and (1, 2/3) showing r ~ 1/3 (circles), and junction YD at (1, 2) and (2, 1) showing r ~ 1/2. d Normalized charge velocities vc/Δν for fractional Δν = 1/3 interface channels at (2/3, 1) and (1, 2/3) marked with circles, integer Δν = 1 interface channels at (1, 2) and (2, 1) marked with squares, and conventional edge channels at (0, 2) and (0, 1) marked with triangles. Data obtained after light irradiation are marked with solid symbols. Channel capacitance C is shown on the right scale.

Full size image

Discussion

The observation above suggests robust fractionalization factors in the disorder-dominated regime. This is consistent with the plasmon (charge density wave) transport model (see Methods) shown in Fig. 5a, where interaction and scattering are characterized by distributed capacitances and scattering conductances, respectively46,47,48. The transport eigenmodes generally deviate from the pure charge and neutral modes at higher frequencies. However, the deviation is small in the low-frequency regime, where the wavelength λ of the plasmon is much greater than the equilibration length leq. This is observed in the numerical simulation of multiple charge fractionalizations with realistic parameters, as shown in Fig. 5b, c, where the distortion of the charge waveform is negligible. The obtained narrow width (a few nanoseconds) of the fractionalized wave packets encourages studying microscopic fractionalization processes including neutral modes and heat generation, which can be used to identify the appropriate effective model34,35,36,49. The deterministic fractionalization processes may benefit the search for non-trivial anyonic statistics of fractional charges48,50,51,52,53.

Fig. 5: Charge fractionalization calculated using a plasmon model.
figure 5

a Non-interacting edge channels Δν = 1 and Δν = 1/3 in the central region and composite Δν = 2/3 channels in the interaction regions on both sides, forming junctions YN and YC. b Time evolution of a charge wave packet initially prepared in the left interacting region at x = −200 μm, showing full transmission and full reflection at YN (x = 0) and charge fractionalization at YC (x = 300 μm). The sum of the currents I1 and I2 in the original Δν = 1 and 1/3 channels, respectively, is plotted in a color scale (red for positive and blue for negative in an arbitrary unit). The numerical simulation was performed using realistic parameters: capacitances C1 = C2 = Cx = 0.07 nF/m; scattering conductance g inducing leq = 10 μm in the interacting regions; C1’ = C2’ = 0.4 nF/m in the non-interaction region. c Time-dependent I1 and I2 at x = 400 μm in right interaction region. Each packet shows I2 = −I1/3 of the charge mode.

Full size image

Methods

Device fabrication

The devices were fabricated from a standard GaAs/AlGaAs heterostructure with a two-dimensional electron gas (2DEG) located 100 nm below the surface having an electron density of 1.85 × 1011 cm−2 in the dark and 2.07 × 1011 cm−2 after light irradiation at low temperature. After patterning holes into the 2DEG for the Corbino geometry, ohmic contacts were formed by alloying Au–Ge–Ni metal films; subsequently metal gates were patterned using photolithography and electron-beam lithography (see Supplementary Note 1 for details).

Time-of-flight experiment

A charge wave packet was generated by depleting electrons near the injection gate GI of length lI ~ 50 μm by applying a voltage step ΔVI = 5–15 mV to the static voltage of −0.2–−0.3 V. This induced charge qI ~ CIlIΔVI in the packet, where CIlI is the coupling capacitance. The charge waveform ρ(t) was evaluated by applying a detector pulse ΔVD = 20 mV to the static voltage of −0.3–−0.4 V on gate GD to change the transmission probability to the detector ohmic contact by ΔTD ~ 0.17. This induced a detector current ID = ΔTDρ(t)tw/Trep with repetition time Trep of the voltage step and the pulse of a width tw = 0.08–0.15 ns. The charge in the wave packet was estimated from the integrated current. The time origin of the delay td was calibrated from a similar experiment at zero magnetic field, where the wave packet propagates much faster with a velocity on the order of 107 m/s16,26,38.

The charge velocity was estimated from the time-of-flight. For the wave packets shown in Fig. 2b, velocities v2/3,u and v1,u of the Δν = 2/3 and 1 channels under the gate (length L) were estimated from the time-of-flight of the first wave packet in traces (i) and (ii), respectively, by disregarding the short time-of-flight (~ 0.5 ns) in the Δν = 2/3 ungated channel39. Subsequently, the velocity v1/3,s of the Δν = 1/3 channel along the side of the gate (length L + 2ℓ) was estimated from the delay of the second wave packet in trace (ii) and the predetermined v1,u. Because the velocity depends strongly on the electrostatic environment, the channels formed along the side of the gates were compared, as shown in Fig. 4d.

Capacitance of interface channel

The interface channel is a compressible stripe of finite width w between two incompressible regions. As the electrostatic potential for this situation is challenging54, we assumed finite widths wg and wu in the gated and ungated regions, respectively, as shown in Fig. 4a. By considering the incompressible regions as insulators, the capacitance between the channel and the gate was calculated using commercial software COMSOL based on the finite-element method.

Fractionalization factor at high frequencies

We used the plasmon scattering approach to simulate the fractionalization process in the presence of disorder-induced tunneling4,46,47. Consider two one-dimensional chiral channels (n = 1 and 2) with conductance σn (positive for right movers and negative for left movers), as shown in Fig. 5a. The charge density ρn, electrochemical potential Vn, and current In = σnVn are related to each other with the Coulomb interaction characterized by the self-capacitance Cn (to the ground) and coupling capacitance CX per unit length16,26. The quantum capacitance was absorbed in those capacitances. Scattering between the channels was considered with scattering conductance g per unit length47. Based on current conservation, we derived the following wave equation:

$$- \frac{\partial }{{\partial x}}\left( {\begin{array}{*{20}{c}} {I_1} \\ {I_2} \end{array}} \right) = \left[ {\left( {\begin{array}{*{20}{c}} {C_1 + C_{\mathrm{x}}} & { - C_{\mathrm{x}}} \\ { - C_{\mathrm{x}}} & {C_2 + C_{\mathrm{x}}} \end{array}} \right)\frac{\partial }{{\partial t}} + g\left( {\begin{array}{*{20}{c}} 1 & { - 1} \\ { - 1} & 1 \end{array}} \right)} \right]\left( {\begin{array}{*{20}{c}} {V_1} \\ {V_2} \end{array}} \right).$$
(1)

Transport eigenmodes \({\hat{\boldsymbol{I}}}_m = \left( {\begin{array}{*{20}{c}} {\tilde I_1} \\ {\tilde I_2} \end{array}} \right)\) can be calculated for alternating current \(I_n = \tilde I_ne^{i\left( {kx - \omega t} \right)}\) with amplitude \(\tilde I_n\) at frequency ω. The resulting k (complex) for each mode measures the wavenumber in the real part and the decay rate in the imaginary part. For the fractional case with σ1 = e2/h, σ2 = −e2/3 h, and g > 0, pure charge and neutral modes with \(\tilde I_2/\tilde I_1 =\) −1/3 and −1, respectively, appeared at g >> ω(C1 + 3C2) in the disorder-dominated regime, and interaction-dependent modes appeared at g << ω(C1 + 3C2) in the interaction-dominated regime. Because the solution in the zero-frequency limit (ω → 0) provides the equilibration length \(l_{\mathrm{eq}} = \sigma _{\mathrm{q}}/2{\mathrm{g}}\), the disorder-dominated regime corresponds to the plasmon wavelength λ much longer than leq. Our wave packet contains a long wavelength in the Fourier components (λ \(\gtrsim\) 800 μm in the Δν = 2/3 channel for the data in Fig. 2b and λ \(\gtrsim\) 300 μm in the Δν = 2 channel for the data in Fig. 2c). Hence, all data shown herein are obtained from the disorder-dominated regime for our sample with leq ~ 10 μm. In this case, the charge mode exhibits a slight decay with an angle \(\arg \left[ k \right]\sim 2{\uppi}\left( {\frac{{C_1 \, + \, 3C_2}}{{C_1 \, + \, C_2}}} \right)^2\,\frac{{l_{\mathrm{eq}}}}{\lambda }\) in the lowest order. This broadens the wave packet only slightly. The time evolutions of I1 and I2 in Fig. 5 were obtained by integrating Eq. (1) with current conservation at the boundaries of non-interacting (CX = 0 and g = 0) and interacting regions.