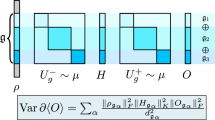
Abstract
Variational quantum computing schemes train a loss function by sending an initial state through a parametrized quantum circuit, and measuring the expectation value of some operator. Despite their promise, the trainability of these algorithms is hindered by barren plateaus (BPs) induced by the expressiveness of the circuit, the entanglement of the input data, the locality of the observable, or the presence of noise. Up to this point, these sources of BPs have been regarded as independent. In this work, we present a general Lie algebraic theory that provides an exact expression for the variance of the loss function of sufficiently deep parametrized quantum circuits, even in the presence of certain noise models. Our results allow us to understand under one framework all aforementioned sources of BPs. This theoretical leap resolves a standing conjecture about a connection between loss concentration and the dimension of the Lie algebra of the circuit’s generators.
Similar content being viewed by others
Introduction
Variational quantum computing schemes, such as variational quantum algorithms1,2,3,4,5,6 or quantum machine learning models7,8,9,10, share a common structure in which quantum and classical resources are used to solve a given task. In a nutshell, these algorithms send some initial state through a parametrized quantum circuit and then perform (a polynomial number of) measurements to estimate the expectation value of some observable that encodes the loss function (also called cost function) appropriate for the problem. Subsequently, the estimated loss (or its gradient) is fed into a classical optimizer that attempts to update the circuit parameters to minimize the loss.
In the past few years, research has started to point towards seemingly fundamental difficulties in training generic parametrized quantum circuits11,12,13. In particular, one of the main obstacles towards trainability is the presence of Barren Plateaus (BPs)13 in the loss function. In the presence of BPs, this loss function (and its gradients) exponentially concentrates in parameter space as the size of the problem increases. Therefore, unless an exponential number of measurement shots are employed, the model becomes untrainable, as one does not have enough precision to find a loss-minimizing direction and navigate the loss landscape.
Due to the tremendous limitations that BPs place on the potential to scale variational quantum computing schemes to large problem sizes, a significant amount of effort has been put forward towards understanding why and when BPs arise. In this context, the presence of BPs (in the absence of noise) has been shown to arise from several disparate aspects of the variational problem, including the expressiveness of parametrized quantum circuits (that is, the breadth of unitaries that the parametrized quantum circuit can express)13,14,15,16,17,18,19,20,21,22,23,24,25, the locality of the loss function measurement operator O26,27,28,29,30,31,32, and the entanglement and randomness of the initial state ρ13,26,33,34,35,36,37. Hardware noise further exacerbates these issues38,39,40. Yet, despite our significant understanding of BPs, most of the results in the literature have been derived or can be applied only for certain circuit architectures or scenarios. Thus, we cannot generalize the lessons learned from one scenario to another, and the different sources of BPs are regarded as independent. In other words, we do not have a unifying holistic theory that can capture the interplay of the various aspects that give rise to BPs.
In this work, we present a general Lie algebraic theory for BPs that can be applied to any deep, unitary, parametrized quantum circuit architecture. Our theory is based on the study of the Lie group and the associated Lie algebra \({\mathfrak{g}}\), which is generated by the parametrized quantum circuit. In turn, this allows us to understand under one single umbrella all known sources of BPs. Critically, we are able to precisely compute the variance of the loss function and, therefore, study its concentration in parameter space, provided that the measured observable O or the circuit’s input state ρ is in. Our results encapsulate the known causes of BPs, as we generalize the concepts of circuit expressiveness, initial state entanglement, operator locality, and hardware noise to a unified framework (see Fig. 1). Moreover, we also provide a quantifiable definition for a deep quantum circuit, as we present rigorous bounds for the number of layers needed for it to be an approximate design over the Lie group \({e}^{{\mathfrak{g}}}\), and for how much the variances for an exact and for an approximate design deviate.
Many works in the literature have shown that BPs can arise from: the expressiveness of the parametrized circuit, the locality of the measurement operator, the entanglement in the initial state, or due to hardware noise. In the figure, we schematically depict these sources as being separate, since their study is usually performed in restricted scenarios, thus limiting our ability to interconnect them. In this work, we present a unified Lie algebraic theory that can be used to study BPs in deep parametrized quantum circuits under SPAM and coherent noise. Our theorems allow us to understand under a single unified framework all sources of BPs by leveraging concepts such as generalized locality entanglement and algebraic decoherence.
Results
Loss function and barren plateaus
In what follows, we will consider problems where an n-qubit state ρ, acting on a Hilbert space \({{{{{{\mathcal{H}}}}}}}={({{\mathbb{C}}}^{2})}^{\otimes n}\), is sent through a parametrized quantum circuit U(θ) of the form
Here, θ = (θ1, θ2, …) is a set of trainable real-valued parameters, and \({H}_{l}\in i{\mathfrak{u}}({2}^{n})\) are Hermitian operators that we collect in a set of generators \({{{{{{\mathcal{G}}}}}}}=\{{H}_{1},{H}_{2},\ldots \}\). At the output of the circuit, one measures some Hermitian observable \(O\in i{\mathfrak{u}}({2}^{n})\), such that \({\left\Vert O\right\Vert }_{2}^{2}\,\le\, {2}^{n}\), leading to the loss function,
Depending on the algorithm at hand, the previous procedure might be repeated for different initial states (e.g., input states coming from some training set), or measurement operators (e.g., measuring different non-commuting observables), and the set of such expectation values can be combined into a more complicated loss function. To account for all of those scenarios, we will simply study a quantity as that in Eq. (2), as we know that if ℓθ(ρ, O) concentrates, then so will any function computed from it.
Finally, we will consider SPAM errors — which we model by adding completely positive and trace-preserving channels \({{{{{{{\mathcal{N}}}}}}}}_{B}\) and \({{{{{{{\mathcal{N}}}}}}}}_{A}\) acting before and after the circuit, respectively — and coherent errors, which we represent as uncontrolled unitary gates interleaved with the parametrized gates. When these sources of noise are present, we write the noisy loss function as
where \(\widetilde{U}({{{{{{\boldsymbol{\theta }}}}}}})={\prod }_{l=1}^{L}{e}^{-i{\alpha }_{l}{K}_{l}}{e}^{i{H}_{l}{\theta }_{l}}\) for fixed (not tunable) real values αl and Hermitian operators Kl.
In what follows, we will study how much the loss ℓθ(ρ, O) (or its noisy counterpart \({\widetilde{\ell }}_{{{{{{{\boldsymbol{\theta }}}}}}}}(\rho,\,O)\)) changes as the parameters θ vary. In particular, we want to characterize the variance of the loss over the parameter landscape,
and we will say that the loss exhibits a BP if the variance vanishes exponentially with the system size, i.e., if \({{{{{{{\rm{Var}}}}}}}}_{{{{{{{\boldsymbol{\theta }}}}}}}}[{\ell }_{{{{{{{\boldsymbol{\theta }}}}}}}}(\rho,\,O)]\in {{{{{{\mathcal{O}}}}}}}(1/{b}^{n})\), for some b > 1. It is important to note that in the literature it is common to study the presence of BPs by analyzing the concentration of the partial derivatives of the loss, i.e., the scaling of \({{{{{{{\rm{Var}}}}}}}}_{{{{{{{\boldsymbol{\theta }}}}}}}}[\frac{\partial {\ell }_{{{{{{{\boldsymbol{\theta }}}}}}}}(\rho,\,O)}{\partial {\theta }_{\mu }}]\). However, since loss concentration implies partial derivative concentration41, in what follows we exclusively focus on the former. Moreover, our results on the variance of the loss function can be modified in a straightforward way to obtain the variance of the partial derivatives.
Dynamical Lie algebra
Computing the variance of the loss function requires evaluating averages over the parameter landscape. When the circuit is sufficiently deep, we can leverage Lie algebraic tools to perform such calculations. To this end, we define the so-called dynamical Lie algebra (DLA)42,43,44 of the parametrized quantum circuit (we will assume a circuit with no coherent errors for the remainder of this section). The DLA is defined as the Lie closure of the circuit’s generators,
which is the (closed under commutation) subspace of \({\mathfrak{u}}({2}^{n})\) spanned by the nested commutators of the generators \(i{{{{{{\mathcal{G}}}}}}}\). Since \({\mathfrak{g}}\) is a subalgebra of the Lie algebra \({\mathfrak{u}}({2}^{n})\) of skew-Hermitian operators acting on \({{{{{{\mathcal{H}}}}}}}\), it is a reductive Lie algebra (see, e.g., ref. 45, Chapter IV). This means that we can express \({\mathfrak{g}}\) as a direct sum of commuting ideals,
where \({{\mathfrak{g}}}_{j}\) are simple Lie algebras for j = 1, …, k − 1 and \({{\mathfrak{g}}}_{k}\) is abelian (so \({{\mathfrak{g}}}_{k}\) is the center of \({\mathfrak{g}}\) and \([{\mathfrak{g}},{\mathfrak{g}}]={{\mathfrak{g}}}_{1}\oplus \cdots \oplus {{\mathfrak{g}}}_{k-1}\) is semisimple). In the Methods we provide additional intuition as to why the DLA takes the form in Eq. (6). The importance of the DLA comes from the fact that it quantifies the ultimate expressiveness of the parametrized quantum circuit: we have \(U({{{{{{\boldsymbol{\theta }}}}}}})\in G={e}^{{\mathfrak{g}}}\) for all θ.
In the following, we assume that the parametrized circuit is deep enough so that it forms a 2-design on each of the simple or abelian components \({G}_{j}={e}^{{{\mathfrak{g}}}_{j}}\) (j = 1, …, k) (i.e., the first two moments of the distribution of unitaries obtained from the circuits, match those of the Haar measure over each group Gj46), which will allow us to compute the variance via an explicit integration over the Lie group. Our results are readily useful to analyze the variance of circuits that form approximate, rather than exact, designs. In particular, in the Methods and the Supplemental Information, we present and prove Theorems 2 and 3, which respectively set bounds on the necessary number of layers for the circuit to become an ϵ-approximate 2-design over G, and bound the difference between the variance of a 2-design circuit and that of an L-layered circuit that does not necessarily form a 2-design over G. Then, for any function f(U(θ)) that is a polynomial of order (up to) two in the matrix elements of U(θ) and its conjugate transpose, we will compute averages over the parameter landscape as \({{\mathbb{E}}}_{{{{{{{\boldsymbol{\theta }}}}}}}}[f(U({{{{{{\boldsymbol{\theta }}}}}}}))]={\prod }_{j=1}^{k}{\int}_{{G}_{j}}d{\mu }_{j}f(U({{{{{{\boldsymbol{\theta }}}}}}}))\), where dμj is the normalized, left- and right-invariant Haar measure on Gj. Such integrals can be evaluated using Weingarten Calculus (see, e.g.,47), and we present a simple approach based on the invariant theory of Lie algebras.
Finally, our results use a generalized notion of purity with respect to an arbitrary operator subalgebra \({\mathfrak{g}}\subseteq {\mathfrak{u}}({2}^{n})\). The \({\mathfrak{g}}\)-purity of a Hermitian operator \(H\in i{\mathfrak{u}}({2}^{n})\) is defined as48,49
where \({H}_{{\mathfrak{g}}}\) denotes the orthogonal projection of H into \({{\mathfrak{g}}}_{{\mathbb{C}}}={{{{{{{\rm{span}}}}}}}}_{{\mathbb{C}}}{\mathfrak{g}}\) (the complexification of \({\mathfrak{g}}\)) and \({\{{B}_{j}\}}_{j=1}^{\dim ({\mathfrak{g}})}\) an orthonormal basis (over \({\mathbb{C}}\)) for \({{\mathfrak{g}}}_{{\mathbb{C}}}\) with respect to the Hilbert–Schmidt inner product \(\left\langle A,B\right\rangle={{{{{{\rm{Tr}}}}}}}[{A}^{{{{\dagger}}} }B]\)45. Note that \({H}_{{\mathfrak{g}}}\in i{\mathfrak{g}}\) and the basis vectors Bj are chosen from \(i{\mathfrak{g}}\); in that case, \({{{{{{\rm{Tr}}}}}}}[{B}_{j}^{{{{\dagger}}} }H]={{{{{{\rm{Tr}}}}}}}[{B}_{j}H]\in {\mathbb{R}}\). In the Supplemental Information, we provide some intuition about why the \({\mathfrak{g}}\)-purity arises as the natural quantity in our results.
Main result
In this section, we present an exact formula for the variance of the loss function. To simplify the presentation, we will first restrict ourselves to noiseless circuits and incorporate noise as we proceed. Our main theorem exploits the reductiveness of the DLA: when either \(\rho \in i{\mathfrak{g}}\) or \(O\in i{\mathfrak{g}}\), the loss (and its variance) can be expanded into individual terms arising from each ideal \({{\mathfrak{g}}}_{j}\subseteq {\mathfrak{g}}\) (see the “Methods” and Supplemental Information for additional details). Equipped with this result, we can prove the following theorem:
Theorem 1
Suppose that \(O\in i{\mathfrak{g}}\) or \(\rho \in i{\mathfrak{g}}\), where the DLA \({\mathfrak{g}}\) is as in Eq. (6). Then the mean of the loss function vanishes for the semisimple component \({{\mathfrak{g}}}_{1}\oplus \cdots \oplus {{\mathfrak{g}}}_{k-1}\) and leaves only abelian contributions:
Conversely, the variance of the loss function vanishes for the center \({{\mathfrak{g}}}_{k}\) and leaves only simple contributions:
Let us now consider the implications of Theorem 1. As we can see from Eq. (8), the mean of the loss is solely determined by the projections of ρ and O onto the center \({{\mathfrak{g}}}_{k}\) of \({\mathfrak{g}}\). As such, if \({\mathfrak{g}}\) is centerless, then \({{\mathbb{E}}}_{{{{{{{\boldsymbol{\theta }}}}}}}}[{\ell }_{{{{{{{\boldsymbol{\theta }}}}}}}}(\rho,\,O)]=0\). Conversely, if \({\mathfrak{g}}\) is abelian and if ρ or O commutes with \({\mathfrak{g}}\) (a slightly more general condition than belonging to \({\mathfrak{g}}\)), then the loss landscape is completely flat.
Next, we turn our attention to Eq. (9). This equation shows that each term in the variance of the loss function depends on three quantities: the dimension of \({{\mathfrak{g}}}_{j}\), and the \({{\mathfrak{g}}}_{j}\)-purities of ρ and O. To understand what each of these terms means, let us focus on the case where \({\mathfrak{g}}\) is simple. Then Eq. (9) has a single term,
The following result, proved in the Supplemental Information, illustrates the fact that BPs can arise from three sources.
Corollary 1
Let \({\left\Vert O\right\Vert }_{2}^{2}\le {2}^{n}\). If either \(\dim ({\mathfrak{g}})\), \(1/{{{{{{{\mathcal{P}}}}}}}}_{{\mathfrak{g}}}(\rho )\) or \(1/{{{{{{{\mathcal{P}}}}}}}}_{{\mathfrak{g}}}(O)\) is in Ω(bn) with b > 2, then the loss has a BP.
In what follows, we analyze these three causes of BPs.
Sources of barren plateaus
(i) Ansatz expressiveness and the DLA. First, we observe from Theorem 1 that the variance is inversely proportional to \(\dim ({\mathfrak{g}})\), which directly quantifies the expressiveness of the circuit; that is, more expressive circuits (with larger \(\dim ({\mathfrak{g}})\)) lead to more concentrated loss functions (see Fig. 2a). In particular, as shown in Corollary 1, if the dimension of the DLA is in Ω(bn) for some b > 2, then the loss is exponentially concentrated regardless of the initial state or measurement operator. Thus, deep circuits with exponential DLAs are always untrainable. On the other hand, if \(\dim ({\mathfrak{g}})\in {{{{{{\mathcal{O}}}}}}}({{{{{{\rm{poly}}}}}}}(n))\) (see examples of polynomially scaling DLAs in refs. 50,51,52,53), the expressiveness of the circuit will not induce BPs by itself. As we will see below, this does not preclude the possibility that the initial state or the measurement operator could still lead to exponential concentration. Importantly, this result proves (under the assumption that ρ or O is in \(i{\mathfrak{g}}\)) the conjecture proposed in ref. 17, where the authors argue precisely that the loss variance should be inversely proportional to the expressive power of the circuit, captured by the DLA dimension.
The “best known” sources of BPs include: (a) circuits that are too expressive with \(\dim ({\mathfrak{g}}) \sim {4}^{n}\), for any O, ρ; (b) highly entangled initial states ρ, even for shallow circuits and local O; (c) global operators O, even for shallow circuits; (d) noise channels. Our framework unifies these sources in one holistic picture, characterizing the circuit expressivity as \(\dim ({\mathfrak{g}})\), the initial state and operator properties by generalized entanglement and locality via \({\mathfrak{g}}\)-purity, and noise channels by algebraic decoherence.
(ii) Initial quantum state ρ. Second, we consider the \({\mathfrak{g}}\)-purity of a quantum state, \({{{{{{{\mathcal{P}}}}}}}}_{{\mathfrak{g}}}(\rho )={{{{{{\rm{Tr}}}}}}}[{\rho }_{{\mathfrak{g}}}^{2}]\). This quantity has been studied in the literature and is known to be a measure of generalized entanglement54,55. As discussed in ref. 55, one can define a generalization of entanglement relative to a subspace of observables rather than the usual approach, where distinguished subsystems are used to define the entanglement. In standard entanglement theory, the preferred subspaces of observables are given by the local operators that act only on each subsystem, and a pure entangled state looks mixed when partially tracing over one of the subsystems (producing a reduced state). This notion can be generalized by imposing that reduced states of a quantum system only provide the expectations of some set of distinguished observables, and we say that a state is generalized unentangled relative to the distinguished observables if its reduced state is pure (cf. Fig. 2b). Taking the subspace of observables to be the DLA leads precisely to this generalized measure of entanglement. In this framework, the purity \({{{{{{{\mathcal{P}}}}}}}}_{{\mathfrak{g}}}(\rho )\) is maximized (ρ is not generalized entangled) if ρ belongs to the orbit of the highest weight state of \({\mathfrak{g}}\) (see Methods for a definition of the highest weight state, as well as a particular case where we specialize to ρ or O simultaneously diagonalizable with a Cartan subalgebra \({\mathfrak{h}}\subseteq {\mathfrak{g}}\)). Essentially, a smaller \({\mathfrak{g}}\)-purity implies larger generalized entanglement and, in turn, smaller variances. Hence, if \({{{{{{{\mathcal{P}}}}}}}}_{{\mathfrak{g}}}(\rho )\in {{{{{{\mathcal{O}}}}}}}(1/{b}^{n})\) (high generalized entangled state), the loss concentrates exponentially regardless of the circuit expressiveness, that is, even if \(\dim ({\mathfrak{g}})\) is polynomial.
(iii) Measurement operator O. Finally, we turn to the \({\mathfrak{g}}\)-purity of the measurement operator O (cf. Fig. 2c). We carry over the notion of generalized entanglement to define a generalized notion of locality: We call an operator O generalized-local if it belongs to the preferred subspace of observables given by \({\mathfrak{g}}\). In this case, \({O}_{{\mathfrak{g}}}=O\). On the other hand, we will call it (fully) generalized nonlocal if \({O}_{{\mathfrak{g}}}=0\). This definition allows us to establish a hierarchy of locality when O belongs to the DLA’s associative algebra (the matrix-product closure of \({\mathfrak{g}}\)). Here, one can classify the amount of generalized locality by expressing O as a polynomial of elements of \({\mathfrak{g}}\), and filter them according to the polynomial’s degree; more local operators will be those that can be expressed as polynomials of lower degree. With the above definition, one can readily see that generalized local operators (i.e., those satisfying \({O}_{{\mathfrak{g}}}=O\)) maximize the variance. On the other hand, when \({O}_{{\mathfrak{g}}}\in {{{{{{\mathcal{O}}}}}}}(1/{b}^{n})\) (highly generalized nonlocal measurements), the loss exhibits a BP regardless of the DLA dimension.
Putting points (i)–(iii) together, our results in Theorem 1 imply that the loss concentration is completely determined by the expressiveness of the parametrized quantum circuit, the generalized entanglement of the input state, and the generalized locality of the measurement operator. When the DLA \({\mathfrak{g}}\) is not simple, in order for the loss to be exponentially concentrated and a BP to occur, each of the components \({{\mathfrak{g}}}_{j}\) needs exponentially large DLAs, highly generalized-entangled states, or very generalized-nonlocal measurements. When this condition is not satisfied on some of the components \({{\mathfrak{g}}}_{j}\), one can train the loss function only on the signal from these components, but only for those particular components \({{\mathfrak{g}}}_{j}\); for the remainder, the variances are exponentially suppressed.
Incorporating the effects of noise
To finish, we consider how SPAM noise and coherent errors affect the variance scaling (cf. Fig. 2d). We begin by considering the case of state preparation noise, assuming \(O\in i{\mathfrak{g}}\). The effect of noise is to change the initial state from ρ to \({{{{{{{\mathcal{N}}}}}}}}_{B}(\rho )\). From Theorem 1, we find that if the \({\mathfrak{g}}\)-purity of the state decreases (in some or all components \({{\mathfrak{g}}}_{j}\) of \({\mathfrak{g}}\)), then so will the variance. This will be the case for global depolarizing noise \({{{{{{{\mathcal{N}}}}}}}}_{B}(\rho )=(1-p)\rho+p{\mathbb{1}}/{2}^{n}\), which takes \({{{{{{{\mathcal{P}}}}}}}}_{{{\mathfrak{g}}}_{j}}(\rho )\) to \({{{{{{{\mathcal{P}}}}}}}}_{{{\mathfrak{g}}}_{j}}({{{{{{{\mathcal{N}}}}}}}}_{B}(\rho ))={(1-p)}^{2}{{{{{{{\mathcal{P}}}}}}}}_{{{\mathfrak{g}}}_{j}}(\rho )\). Moreover, we can see that even local unitaries acting on a single qubit during state preparation (which would preserve the standard purity \({{{{{{\rm{Tr}}}}}}}[{\rho }^{2}]\) of the state and the standard entanglement) can lead to a generalized-entanglement-induced loss concentration if they rotate the state outside of \(i{\mathfrak{g}}\). These examples showcase a form of algebraic decoherence, whereby the state gets entangled with either an actual environment (e.g., the previous case of depolarizing noise) or with an effective “algebraic environment” within the system.
Next, we consider the presence of measurement errors. We can model this with a channel \({{{{{{{\mathcal{N}}}}}}}}_{A}^{-1}\) acting on O, where \({{{{{{{\mathcal{N}}}}}}}}_{A}^{-1}\) denotes the inverse of the noise channel \({{{{{{{\mathcal{N}}}}}}}}_{A}\), which is generally not a physical quantum channel. In this case, if the \({\mathfrak{g}}\)-purity of the measurement operator decreases, i.e., if O loses generalized locality, then the loss concentrates.
Finally, we study the effect of coherent errors that occur during circuit execution. In this case, we can model their impact as uncontrolled unitaries acting along the circuit, which will change the set of generators to \(\widetilde{{{{{{{\mathcal{G}}}}}}}}={{{{{{\mathcal{G}}}}}}}\cup \{i{K}_{l}\}\), and thus the DLA becomes \(\widetilde{{\mathfrak{g}}}\supseteq {\mathfrak{g}}\). Interestingly, this means that coherent noise can increase the expressiveness of the circuit at the cost of potentially decreasing the variance. To know exactly how the variance changes, one needs to study the reductive decomposition of \(\widetilde{{\mathfrak{g}}}\), as well as the \(\widetilde{{\mathfrak{g}}}\)-purities of ρ and O in this new noise-induced DLA.
Discussion
Finding ways to avoid or mitigate barren plateaus (BPs) has been one of the central topics of research in variational quantum computing. This has led the community to develop a series of good practice guidelines such as: “global observables where one measures all qubits are untrainable” or “too much entanglement leads to BPs.” While these are widely regarded as being universally true, they are in fact obtained by extrapolating results derived for a specific circuit architecture and assuming that they will hold in another. Many of these misconceptions are propagated due to a lack of a single unifying theory of BPs that truly connects the results obtained for different architectures. In this work, we present one such theory based on the Lie algebraic properties of the parametrized quantum circuit, the initial state, and the measurement operator.
Despite the relative simplicity of our main theorem, its implications are extremely important to the field of variational quantum computing. First, it is worth highlighting that, unlike other results, our theorems provide exact variance calculations rather than upper or lower bounds, thus allowing us to precisely determine whether we will or will not have a BP. Second, we note that our theorem applies to any (noiseless) deep parametrized quantum circuit, independent of its structure, but requiring only knowledge of the DLA of the circuit (and provided that ρ or O are in \(i{\mathfrak{g}}\)). This makes our results applicable in essentially all areas of variational quantum computing. Conceptually, our results uncover the precise role that entanglement and locality play in the nature of BPs. However, they do so by being defined in terms of the operators in the DLA rather than in terms of local operators determined by the qubit-subsystem decomposition. As such, it is entirely possible for a circuit to be trained on highly entangled initial states using highly nonlocal measurements (i.e., acting on all qubits) as long as they are well aligned with the underlying DLA of the circuit. This goes against one of the best practices in the field and demonstrates that a more subtle approach is valuable. It is also worth noting that our algebraic formalism allows us to consider simple noise models such as SPAM errors and coherent noise. Our analysis shows that noise-induced concentration can be understood as building generalized entanglement in the initial state, reducing the generalized locality of the measurement observable, or increasing the expressive power of the circuit.
Looking ahead, we see different ways to extend our results. For example, our theorems are derived for the case where ρ or O is in \(i{\mathfrak{g}}\). Although this case encompasses most algorithms in the literature1,2,3, it could be interesting to generalize our results to operators and measurements not in the DLA. We refer the readers to ref. 56, where exact loss function variance calculations are presented for a parametrized matchgate circuit, which is valid for arbitrary measurements and initial states. We hope that the results therein will serve as a blueprint for a general theory for generic circuits. Moreover, one can also envision considering more realistic noise settings where noise channels are interleaved with the unitaries. Clearly, since a noisy parametrized quantum circuit no longer forms a group, our Lie algebraic formalism no longer applies. Similarly, we encourage the community to develop tools to compute the exact variance for circuits that do not form approximate 2-designs, as these cases are not covered by our main theorems. In this case, a Lie algebraic treatment such as the one presented here will not be available. Here, one will have to instead make additional assumptions such as local gates being sampled from a local group, thus mapping the variance evaluation to a Markov chain-like process which can be analyzed analytically21,26,27,57,58,59,60,61,62,63,64, numerically via Monte Carlo65 and tensor networks66,67, or studied via XZ-calculus68. Moreover, we note that recent results have tied the DLA and the presence or absence of barren plateaus to other phenomena like the simulability of the quantum model56,69, to the presence of local minima in the optimization landscape70, and to the reachability of solutions (through the disconnectedness in the geometric manifold of unitaries71). We expect that in the near future, the generalized notions of entanglement and locality discussed here will be connected to the resources needed to make a model more or less universal, more or less simulable, and more or less trainable. Such connections will shed additional light on the central role that the DLA plays in characterizing variational quantum computing models.
Note added. A few days before our work was submitted to the arXiv, the manuscript72 was posted as a preprint. In ref. 72, the authors provide an independent proof of the conjecture in17 and present results similar to those in our theorems and examples. However, we note that in Ref. 72 the authors study partial derivative concentration rather than loss concentration as we do. Moreover, our work provides a novel conceptual understanding of the variance \({\mathfrak{g}}\)-purity terms as forms of generalized entanglement and locality. As such, our work complements that of72, and we encourage the reader to review both manuscripts.
Methods
In this section, we first recall a few basic concepts for the DLA, present examples that showcase how our results can be used to understand several BP results in the literature (see Fig. 2) and derive additional theorems that justify some of the assumptions made in the main text. We also present concrete examples where we can analytically compute the \({\mathfrak{g}}\)-purities of the state and the measurement operator. Furthermore, in the Supplemental Information, we include numerical simulations that illustrate our theoretical findings.
Symmetries and the DLA structure
In Eq. (6) we have argued that the DLA can be generically decomposed as a direct sum of commuting ideals. Here we provide additional intuition as to why this is the case. First, let us begin by denoting as \({{{{{{\rm{comm}}}}}}}({{{{{{\mathcal{G}}}}}}})\) the commutant of the set of generators \({{{{{{\mathcal{G}}}}}}}\) (i.e., the symmetries of the gate generators), that is,
and as \({\mathfrak{z}}\) the center of \({{{{{{\rm{comm}}}}}}}({{{{{{\mathcal{G}}}}}}})\), i.e.,
The importance of the commutant \({{{{{{\rm{comm}}}}}}}({{{{{{\mathcal{G}}}}}}})\) and its center \({\mathfrak{z}}\) span from the fact that they determine the invariant subspaces of the Hilbert space under the action of \(G={e}^{{\mathfrak{g}}}\). Moreover, the dimension of the center is directly related to the DLA’s decomposition as we can rewrite the decomposition of \({\mathfrak{g}}\) into commuting ideals as
with mλ denoting the multiplicity of the representation \({{\mathfrak{g}}}_{\lambda }\) of \({\mathfrak{g}}\). We may interpret such a direct sum decomposition as saying, “There exists a basis of our Hilbert space that block-diagonalizes the matrices in \({\mathfrak{g}}\).”
Equation (13) shows that a circuit with symmetries will have a rich and complex DLA structure, while universal, unstructured circuits will likely lead to controllable circuits with \({\mathfrak{g}}={\mathfrak{su}}({2}^{n})\). In particular, we note that while there have been significant recent efforts on computing DLAs44,50,51,52,53,71,73, this field is still in its infancy, and we predict that as our understanding and ability to calculate the DLA increases, the results of the present work will become more and more important for studying the trainability of structured parametrized quantum circuits.
Examples of barren plateaus and their origins
In this section, we review some results in the literature that have studied different sources of BPs, and we show how these results can be understood by our framework.
(i) Expressiveness. One of the most studied sources of BPs is the expressiveness of the circuit13,14,15,16,17,18,19,20,21,22,23,24,25. As previously noted, by expressiveness we mean the breadth of unitaries that the circuit can generate as the parameters are varied.
For example, let us consider the case where the unitary U(θ) forms a 2-design46 over \({\mathbb{SU}}({2}^{n})\) (see Fig. 2a). This is precisely the case studied in the seminal work of Ref. 13. Here, \({\mathfrak{g}}={\mathfrak{su}}({2}^{n})\), meaning that \(\dim ({\mathfrak{g}})={4}^{n}-1\). From Theorem 1, we find \({{\mathbb{E}}}_{{{{{{{\boldsymbol{\theta }}}}}}}}[{\ell }_{{{{{{{\boldsymbol{\theta }}}}}}}}(\rho,\,O)]=0\) (because the Lie algebra has no center), and
In the second line above, we have used the fact that, because \(i{\mathfrak{su}}({2}^{n})\) contains all Pauli matrices except the identity \({\mathbb{1}}\), we have \({O}_{{\mathfrak{g}}}=O-{2}^{-n}{{{{{{\rm{Tr}}}}}}}[O]{\mathbb{1}}\) and similarly for ρ (which has \({{{{{{\rm{Tr}}}}}}}[\rho ]=1\)). Since \({{{{{{\rm{Tr}}}}}}}[{O}^{2}]\le {2}^{n}\) (by assumption) and noting that \({{{{{{\rm{Tr}}}}}}}[{\rho }^{2}]-{2}^{-n}\le 1\), we find that \({{{{{{{\rm{Var}}}}}}}}_{{{{{{{\boldsymbol{\theta }}}}}}}}[{\ell }_{{{{{{{\boldsymbol{\theta }}}}}}}}(\rho,\,O)]\in {{{{{{\mathcal{O}}}}}}}(\frac{1}{{2}^{n}})\). Hence, we can see that, regardless of what O and ρ are, the expressiveness of the circuit will always lead to a BP.
(ii) Measurement locality. A second potential source of BPs is the measurement operator26,27,28,29,30,31,32. For example, consider the task of sending \(\rho=\left\vert 0\right\rangle {\left\langle 0\right\vert }^{\otimes n}\) through a circuit U(θ) composed of general single-qubit gates. Clearly, this parametrized quantum circuit is very inexpressive as it does not generate entanglement; in fact, we can easily find that \({\mathfrak{g}}={\mathfrak{su}}{(2)}^{\oplus n}\). As shown in ref. 26, if the measurement is global (see Fig. 2c), e.g., O = X⊗n, one has a BP since \({{{{{{{\rm{Var}}}}}}}}_{{{{{{{\boldsymbol{\theta }}}}}}}}[{\ell }_{{{{{{{\boldsymbol{\theta }}}}}}}}(\rho,\,O)]\in {{{{{{\mathcal{O}}}}}}}(1/{2}^{n})\). However, measuring an operator in \({\mathfrak{g}}\), such as O = X1 (see Fig. 2c), does not lead to BPs. Now Theorem 1 indicates that \({{\mathbb{E}}}_{{{{{{{\boldsymbol{\theta }}}}}}}}[{\ell }_{{{{{{{\boldsymbol{\theta }}}}}}}}(\rho,\,O)]=0\) and
where \({{{{{{{\rm{Tr}}}}}}}}_{{{\mathbb{C}}}^{2}}\) denotes the trace over the qubit where O acts. Indeed, we have \({\mathfrak{g}}={{\mathfrak{g}}}_{1}\oplus \cdots \oplus {{\mathfrak{g}}}_{n}\) with each \({{\mathfrak{g}}}_{j}\cong {\mathfrak{su}}(2)\). Using the orthonormal basis {2−n/2Xj, 2−n/2Yj, 2−n/2Zj} of \(i{{\mathfrak{g}}}_{j}\), we find \({O}_{{{\mathfrak{g}}}_{1}}={X}_{1}\) and \({O}_{{{\mathfrak{g}}}_{j}}=0\) for 2 ≤ j≤ n, while \({\rho }_{{{\mathfrak{g}}}_{j}}={2}^{-n}{Z}_{j}\) for all j. This gives \({{{{{{\rm{Tr}}}}}}}[{O}_{{{\mathfrak{g}}}_{1}}^{2}]={2}^{n}\), \({{{{{{\rm{Tr}}}}}}}[{\rho }_{{{\mathfrak{g}}}_{1}}^{2}]={2}^{-n}\), yielding the value 1/3 on the second line of Eq. (15). The last line in Eq. (15) provides an alternative interpretation, where the observable O and state ρ are reduced on the first qubit to O1 = X and \({\rho }_{1}=\left\vert 0\right\rangle \left\langle 0\right\vert\), respectively. Note that the last line in Eq. (15) is the special case n = 1 of Eq. (14). Thus, in this specific case, the notions of generalized entanglement and generalized locality match their standard notions based on the subsystem decomposition of the Hilbert space. As such, if we measure a local operator in qubit j, the variance will depend on the purity of the reduced (input) state over qubit j.
(iii) Initial state entanglement. Next, it has been shown that initial state entanglement can lead to BPs13,26,33,34,35,36,37. For instance, consider again the circuit in Fig. 2c, where U(θ) is composed of single qubit gates, and let the measurement operator be local, e.g., O = X1. Although we do not expect expressiveness- or locality-induced BPs, if the initial state ρ satisfies a volume law of entanglement (i.e., if the reduced state on any qubit is exponentially close to being maximally mixed), then \({{{{{{{\rm{Tr}}}}}}}}_{{{\mathbb{C}}}^{2}}[{\rho }_{1}^{2}]\in {{{{{{\mathcal{O}}}}}}}(1/{2}^{n})\) and the loss has a BP according to Eq. (15).
(iv) Noise. Finally, the presence of hardware noise has been shown to induce loss function concentration38,39,40. As an example, consider the circuit in Fig. 2d, where a global depolarizing noise channel \({{{{{{{\mathcal{N}}}}}}}}_{B}(\rho )=(1-p)\rho+p\,{2}^{-n}{\mathbb{1}}\) acts at the beginning of the circuit (e.g., as part of the SPAM errors). Now, we have \({\widetilde{\ell }}_{{{{{{{\boldsymbol{\theta }}}}}}}}(\rho,\,O)=(1-p){\ell }_{{{{{{{\boldsymbol{\theta }}}}}}}}(\, \rho,\,O)+p\,{2}^{-n}{{{{{{\rm{Tr}}}}}}}[O]\). As p increases, we can see that \({{{{{{{\rm{Var}}}}}}}}_{{{{{{{\boldsymbol{\theta }}}}}}}}[{\widetilde{\ell }}_{{{{{{{\boldsymbol{\theta }}}}}}}}(\rho,\,O)]={(1-p)}^{2}{{{{{{{\rm{Var}}}}}}}}_{{{{{{{\boldsymbol{\theta }}}}}}}}[{\ell }_{{{{{{{\boldsymbol{\theta }}}}}}}}(\, \rho,\,O)]\) approaches 0 and the loss concentrates around \({2}^{-n}{{{{{{\rm{Tr}}}}}}}[O]\).
Deep parametrized quantum circuits form 2-designs
Let us here show that if the circuit is deep enough, then it will form a 2-design on each of the simple or abelian components of the DLA. In particular, we answer the question: How many layers are needed for U(θ) to become an approximate 2-design over G?
First, let us express the parametrized quantum circuit by factorizing it into layers. That is, we take U(θ) = UL(θL)UL−1(θL−1) ⋯ U1(θ1) where each layer Ul(θl) is given by \({U}_{l}({{{{{{{\boldsymbol{\theta }}}}}}}}_{l})={\prod }_{k=1}^{K}{e}^{-i{H}_{k}{\theta }_{l,k}}\). Next, let us denote the ensemble of unitaries generated by the L-layered circuit U(θ) by \({{{{{{{\mathcal{E}}}}}}}}_{L}\), and its t-th moment operator \({{{{{{{\mathcal{M}}}}}}}}_{{{{{{{{\mathcal{E}}}}}}}}_{L}}^{(t)}:{\mathfrak{gl}}({{{{{{{\mathcal{H}}}}}}}}^{\otimes t})\to {\mathfrak{gl}}({{{{{{{\mathcal{H}}}}}}}}^{\otimes t})\) is the linear superoperator given by
The importance of \({{{{{{{\mathcal{M}}}}}}}}_{{{{{{{{\mathcal{E}}}}}}}}_{L}}^{(t)}\) arises from the fact that it allows us to compare how expressive, or how close, a given U(θ) is to the Haar ensemble over G. In particular, denoting as \({{{{{{{\mathcal{M}}}}}}}}_{G}^{(t)}\) the moment operator for the Haar ensemble over G, one can quantify the expressiveness of the circuit via the norm of the superoperator,
For our purposes, we work with the Schatten p-norms where p = 1, ∞ on the spaces of operators \({\mathfrak{gl}}({{{{{{{\mathcal{H}}}}}}}}^{\otimes t})\). Both are spectral norms: given the singular values si(A)≥0 of A, we may express these norms as
This induces corresponding operator norms for superoperators \({{{{{{\mathcal{M}}}}}}}:{\mathfrak{gl}}({{{{{{{\mathcal{H}}}}}}}}^{\otimes t})\to {\mathfrak{gl}}({{{{{{{\mathcal{H}}}}}}}}^{\otimes t})\) by the usual
We say \({{{{{{{\mathcal{E}}}}}}}}_{L}\) forms a Gt-design if \({{{{{{{\mathcal{A}}}}}}}}_{{{{{{{{\mathcal{E}}}}}}}}_{L}}^{(t)}=0\), and we say \({{{{{{{\mathcal{E}}}}}}}}_{L}\) forms an ϵ-approximate Gt-design if \({\left\Vert {{{{{{{\mathcal{A}}}}}}}}_{{{{{{{{\mathcal{E}}}}}}}}_{L}}^{(t)}\right\Vert }_{\infty }\le \epsilon\) for some ϵ > 0. We prove the following theorem in the Supplemental Information:
Theorem 2
The ensemble of unitaries \({{{{{{{\mathcal{E}}}}}}}}_{L}\subseteq G\) generated by an L-layered circuit U(θ) will form an ϵ-approximate G 2-design, when the number of layers L is
where \({{{{{{{\mathcal{E}}}}}}}}_{1}\) is the ensemble generated by a single layer U1(θ1).
We actually prove that this is true for any t, but to estimate the variance we need only t = 2.
First, we note that Theorem 2 generalizes the result of17, which was only valid for problems where \({\mathfrak{g}}={\mathfrak{su}}({2}^{n})\) or \({\mathfrak{u}}({2}^{n})\), to the case of an arbitrary DLA. Next, we can explicitly see that if the circuit is deep enough, i.e., if it has enough layers, it will always form an ϵ-approximate G 2-design, thus justifying the assumptions made in the main text. More concretely, if we know what the expressiveness for one layer is, Theorem 2 allows us to compute exactly how many layers are needed for \({\left\Vert {{{{{{{\mathcal{A}}}}}}}}_{{{{{{{{\mathcal{E}}}}}}}}_{L}}^{(t)}\right\Vert }_{\infty }\) to be smaller than a given ϵ. We present in the Supplemental Information an example where we can explicitly construct \({{{{{{{\mathcal{A}}}}}}}}_{{{{{{{{\mathcal{E}}}}}}}}_{1}}^{(2)}\) and obtain its largest eigenvalue. Finally, we note that the expressiveness of a single layer will depend on several choices in the ansatz such as how the gates are distributed in a single layer, and how the parameters are sampled therein. We leave the study of the single-layer expressiveness changes as a function of those factors for future work.
Variance for a circuit that does not form a 2-design over G
In the main text, we have assumed that the circuit is deep enough so that it forms a 2-design over G, and Theorem 2 provides bounds on the necessary number of layers for this to happen. Here, we instead ask the question: How different will the variance be from that in Theorem 1 if the circuit forms approximate, rather than an exact, 2-design over G?
For this purpose, let us consider an L-layered circuit such as that in Eq. (1). In what follows, we do not assume that the circuit forms an approximate 2-design over G. Just as before, we denote the ensemble of unitaries generated by the L-layered circuit U(θ) by \({{{{{{{\mathcal{E}}}}}}}}_{L}\), and we define its t-th moment superoperator \({{{{{{{\mathcal{M}}}}}}}}_{{{{{{{{\mathcal{E}}}}}}}}_{L}}\) by Eq. (16). Then, denoting as \({{{{{{{\rm{Var}}}}}}}}_{{{{{{{{\mathcal{E}}}}}}}}_{L}}\) and VarG the variance obtained by sampling circuits over the distribution \({{{{{{{\mathcal{E}}}}}}}}_{L}\) and over the Haar measure over G, respectively, we find that the following theorem holds.
Theorem 3
Let \({\mathfrak{g}}\subseteq {\mathfrak{u}}({2}^{n})\) be any dynamical Lie algebra, and suppose either ρ or O are in \(i{\mathfrak{g}}\) with ρ a density matrix. Then the difference between the loss function variance of an L-layered circuit, with ensemble of unitaries \({{{{{{{\mathcal{E}}}}}}}}_{L}\), and the variance for a circuit that forms a 2-design over G can be bounded as
where the usual Schatten p-norm and induced Schatten p-norm are given by Eq. (18) and Eq. (19).
Theorem 3 shows that the variance of an L-layered circuit will converge exponentially fast in L to the variance obtained by assuming that U(θ) forms a 2-design. The rate of convergence is again determined by the single layers expressiveness \({\left\Vert {{{{{{{\mathcal{A}}}}}}}}_{{{{{{{{\mathcal{E}}}}}}}}_{1}}^{(2)}\right\Vert }_{\infty }\). As such, we can see that the assumption of U being a 2-design rapidly becomes an exact statement in the deep circuits regime. The proof of Theorem 3 is given in the Supplemental Information.
Variance as a sum over simple or abelian components
As noted in the main text, the DLA can always be decomposed into a direct sum as in Eq. (6). This implies that since G is compact, it must decompose as G = G1 × ⋯ × Gk, with \({G}_{j}={e}^{{{\mathfrak{g}}}_{j}}\). Hence, any parametrized quantum circuit U(θ) ∈ G can be expressed as a tuple U = (U1, …, Uk), where we have omitted the dependence on θ for simplicity of notation. This realization allows us to show that the loss splits into a sum over the summands \({{\mathfrak{g}}}_{j}\) in Eq. (6). Explicitly, for the case where \({\mathfrak{g}}={{\mathfrak{g}}}_{1}\oplus {{\mathfrak{g}}}_{2}\) with \(O\in i{\mathfrak{g}}\) and U(θ) ∈ G, we have
where \({O}_{j}\in {{\mathfrak{g}}}_{j}\) and Uj ∈ Gj for j = 1, 2. Hence, the loss function is
Since \({O}_{1}\in {{\mathfrak{g}}}_{1}\) commutes with any element of G2, we obtain
A similar result holds for the term \({{{{{{\rm{Tr}}}}}}}[\rho U{({{{{{{\boldsymbol{\theta }}}}}}})}^{{{{\dagger}}} }{O}_{2}U({{{{{{\boldsymbol{\theta }}}}}}})]\), and the loss function is expressible as a sum of losses in each simple or abelian component:
Therefore, the mean value and the variance of ℓθ(ρ, O) can also be expressed as the sum of individual terms in each simple or abelian component (additional details of the proof are provided in the Supplemental Information). This statement is formally captured as follows:
Proposition 1
Let O be in \(i{\mathfrak{g}}\) such that \(O={\sum }_{i=1}^{k}{O}_{i}\) respect the decomposition Eq. (6) of \({\mathfrak{g}}\) into simple and abelian components. Then, for any ρ, the expectation and variance of the loss function split into sums as
where \({\ell }_{i}(\rho,{O}_{i})={{{{{{\rm{Tr}}}}}}}[(1,\ldots,{U}_{i},\ldots,1)\rho {(1,\ldots,{U}_{i},\ldots,1)}^{{{{\dagger}}} }{O}_{i}]\) corresponds to the loss in the Gi-component of G.
We note that the previous result is equivalently valid if one exchanges the roles of O and ρ, that is, if \(\rho \in i{\mathfrak{g}}\) and O is any Hermitian observable.
Special case: ρ or O simultaneously diagonalizable with a Cartan subalgebra
Here, we focus on the case where one chooses a Cartan subalgebra \({\mathfrak{h}}\subset {\mathfrak{g}}\) and ρ (or O) is simultaneously diagonalizable with \({\mathfrak{h}}\), i.e., \([\rho,{\mathfrak{h}}]=0\). A basis of \({{{{{{\mathcal{H}}}}}}}\) diagonalizing \({\mathfrak{h}}\) is called a weight basis, and when ρ is diagonalized by this basis, the \({\mathfrak{g}}\)-purity is straightforward to compute. We first demonstrate this situation by revisiting a calculation from ref. 17, which concerns the case where \({\mathfrak{g}}={\mathfrak{su}}(2)\) is irreducibly represented in \({{{{{{\mathcal{H}}}}}}}\). We then generalize this calculation to an arbitrary simple DLA \({\mathfrak{g}}\).
Let \({\mathfrak{g}}\) be the irreducible spin-S representation of \({\mathfrak{su}}(2)\) acting on \({{{{{{\mathcal{H}}}}}}}={{\mathbb{C}}}^{2S+1}\). We have a basis for \(i{\mathfrak{g}}\) given by the usual Hermitian spin matrices \(\{{S}_{x},\,{S}_{y},\,{S}_{z}\}\subseteq {\mathfrak{gl}}({{{{{{\mathcal{H}}}}}}})\). One can pick the Cartan subalgebra \(i{\mathfrak{h}}={{{{{{{\rm{span}}}}}}}}_{{\mathbb{R}}}({S}_{z})\). A convenient orthonormal basis for \({{{{{{\mathcal{H}}}}}}}\) is then given by \(\{\left\vert m\right\rangle \}\), the eigenvectors of Sz, which satisfy
Let us consider the case where \(\rho=\left\vert m\right\rangle \left\langle m\right\vert\) and \(O\in i{\mathfrak{g}}\). To use Theorem 1, we will need to compute \({\rho }_{{\mathfrak{g}}}\). Such projection can be easily computed by performing a change of basis of \({{\mathfrak{g}}}_{{\mathbb{C}}}={{{{{{{\rm{span}}}}}}}}_{{\mathbb{C}}}{\mathfrak{g}}\) from the spin matrices to {S0, S+, S−}, where
with the c’s being normalization constants such that \({{{{{{\rm{Tr}}}}}}}[{S}_{0}^{2}]=1\) and \({{{{{{\rm{Tr}}}}}}}[{S}_{+}^{{{{\dagger}}} }{S}_{+}]={{{{{{\rm{Tr}}}}}}}[{S}_{-}^{{{{\dagger}}} }{S}_{-}]=1\) (in particular we find that \({c}_{z}={{{{{{\rm{Tr}}}}}}}[{S}_{z}^{2}]= \frac{1}{3}S(S+1)(2S+1)\)). On the basis \(\{\left\vert m\right\rangle \}\) of \({{{{{{\mathcal{H}}}}}}}\), Sz is diagonal, S+ is upper triangular nilpotent, and S− is lower triangular nilpotent. A direct calculation shows that \({{{{{{\rm{Tr}}}}}}}[{S}_{+}^{{{{\dagger}}} }\rho ]={{{{{{\rm{Tr}}}}}}}[{S}_{-}^{{{{\dagger}}} }\rho ]=0\), and thus
Then, replacing Eq. (25) into Theorem 1 and using \(\dim ({\mathfrak{g}})=3\) leads to
Note that S(S + 1) is exactly the action of the Casimir element on \({{{{{{\mathcal{H}}}}}}}\). For the case of O = Sz/S (where we normalized the measurement operator so that \(\left\Vert O\right\Vert=1\)), we find that Eq. (26) becomes \({{{{{{{\rm{Var}}}}}}}}_{{{{{{{\boldsymbol{\theta }}}}}}}}[{\ell }_{{{{{{{\boldsymbol{\theta }}}}}}}}(\rho,\,O)]=\frac{{m}^{2}}{3{S}^{2}}\). Hence, we can see that the loss function concentrates depending on the value m, i.e., on the \({\mathfrak{g}}\)-purity or the generalized entanglement present in the initial state.
The previous example can be used as a starting point to calculate the loss variance for ρ being a sum of weight states. In particular, consider the case where \({\mathfrak{g}}\) is simple. We can always find an orthonormal basis of weight spaces for \({{{{{{\mathcal{H}}}}}}}\) by simultaneously diagonalizing a Cartan subalgebra \({\mathfrak{h}}\) of \({\mathfrak{g}}\). This means that we have an orthonormal basis \(\{\left\vert v\right\rangle \}\) for \({{{{{{\mathcal{H}}}}}}}\), so that \(\left\vert v\right\rangle\) has weight λv, i.e.
Note that the eigenvalues λv(Hj) are real as Hj are Hermitian. Then a pure weight state with respect to \({\mathfrak{h}}\) has the form \(\rho=\left\vert v\right\rangle \left\langle v\right\vert\). We say that ρ is a weight state if it is diagonal with respect to the weight basis, i.e., if
As shown in the Supplemental Information, given an orthonormal basis \({\{{H}_{j}\}}_{j=1}^{\dim ({\mathfrak{h}})}\) of \(i{\mathfrak{h}}\), one can find that
Hence,
Then, plugging into Theorem 1 yields the following corollary.
Corollary 2
Let \({\mathfrak{g}}\) be a simple Lie algebra with a Cartan subalgebra \({\mathfrak{h}}\). Let \(O\in i{\mathfrak{g}}\), and ρ be a density matrix with \([\rho,{\mathfrak{h}}]=0\), that is, a weight state as in Eq. (28). Then the variance of the loss function is given by
Here, we find it important to make three remarks. First, by symmetry, the result of Corollary 2 also holds when the roles of ρ and O are reversed, i.e., when \(\rho \in i{\mathfrak{g}}\) and \([O,{\mathfrak{h}}]=0\). Second, the variance does not depend on the choice of Cartan subalgebra, only on the norm of the weight λρ corresponding to the weight state ρ, because all Cartan subalgebras are conjugate to each other. Finally, we note that among all weights λv in an irreducible representation \({{{{{{\mathcal{H}}}}}}}\), the norm \(\left\Vert {\lambda }_{v}\right\Vert\) is maximized when \(\left\vert v\right\rangle\) is the highest weight vector \(\left\vert hw\right\rangle\). Thus, Eq. (31) implies that among all weight states as in Eq. (28), the variance is maximized when ρ is a highest weight state:
From here, we can derive an estimate for the variance as follows. Consider the bilinear form on \({\mathfrak{g}}\) given by \((A,B)={{{{{{{\rm{Tr}}}}}}}}_{{{\mathbb{C}}}^{N}}[AB]\) where the trace is taken over the defining representation \({{\mathbb{C}}}^{N}\) of \({\mathfrak{g}}={\mathfrak{su}}(N)\), \({\mathfrak{so}}(N)\) or \({\mathfrak{sp}}(N)\); this is the standard bilinear form normalized so that (H, H) = 2 or 4 for simple coroots \(H\in i{\mathfrak{h}}\) (for \({\mathfrak{g}}={\mathfrak{su}}(N)\), these are the diagonal matrices with 0, …, 0, 1, − 1, 0, …, 0 on the diagonal). The highest weight λhw of every irreducible finite-dimensional representation \({{{{{{\mathcal{H}}}}}}}\) of \({\mathfrak{g}}\) has the property that λhw(H) is a non-negative integer for any simple coroot H. We assume that these values will not grow with the system size n. Noting that \(\left\langle A,B\right\rangle=\frac{\dim ({{{{{{\mathcal{H}}}}}}})}{N}(A,B)\) for Herimitian operators \(A,B\in i{\mathfrak{g}}\), we see that the basis vectors Hj of \(i{\mathfrak{h}}\) scale as \(\sqrt{N/{2}^{n}}\) times the simple coroots of \(i{\mathfrak{h}}\). Therefore,
Plugging this in Eq. (31), we obtain the upper bound
Hence, we see that if \({{{{{{\rm{Tr}}}}}}}[{O}^{2}]\le {2}^{n}\) and \(\dim ({\mathfrak{g}})\in \Omega ({b}^{n})\) with b > 1, then \({{{{{{{\rm{Var}}}}}}}}_{{{{{{{\boldsymbol{\theta }}}}}}}}[{\ell }_{{{{{{{\boldsymbol{\theta }}}}}}}}(\rho,\,O)]\in {{{{{{\mathcal{O}}}}}}}\big(\frac{1}{\sqrt{{b}^{n}}}\big)\); indicating that if the DLA is simple and of exponential dimension, then the loss will always have a BP regardless of the measurement operator and initial state.
Reporting summary
Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.
Data availability
Data generated and analyzed during the current study are available from the corresponding author upon reasonable request.
References
Cerezo, M. et al. Variational quantum algorithms. Nat. Rev. Phys. 3, 625–644 (2021).
Bharti, K. et al. Noisy intermediate-scale quantum algorithms. Rev. Mod. Phys. 94, 015004 (2022).
Endo, S., Cai, Z., Benjamin, S. C. & Yuan, X. Hybrid quantum-classical algorithms and quantum error mitigation. J. Phys. Soc. Jpn 90, 032001 (2021).
Peruzzo, A. et al. A variational eigenvalue solver on a photonic quantum processor. Nat. Commun. 5, 1 (2014).
Farhi, E., Goldstone, J., & Gutmann, S. A quantum approximate optimization algorithm. Preprint at arXiv https://doi.org/10.48550/arXiv.1411.4028 (2014).
Hadfield, S. et al. From the quantum approximate optimization algorithm to a quantum alternating operator ansatz. Algorithms 12, 34 (2019).
Schuld, M., Sinayskiy, I. & Petruccione, F. An introduction to quantum machine learning. Contemp. Phys. 56, 172 (2015).
Biamonte, J. et al. Quantum machine learning. Nature 549, 195 (2017).
Benedetti, M., Lloyd, E., Sack, S. & Fiorentini, M. Parameterized quantum circuits as machine learning models. Quantum Sci. Technol. 4, 043001 (2019).
Havlíček, V. et al. Supervised learning with quantum-enhanced feature spaces. Nature 567, 209 (2019).
Anschuetz, E. R. & Kiani, B. T. Beyond barren plateaus: Quantum variational algorithms are swamped with traps. Nat. Commun. 13, 7760 (2022).
Bittel, L. & Kliesch, M. Training variational quantum algorithms is NP-hard. Phys. Rev. Lett. 127, 120502 (2021).
McClean, J. R., Boixo, S., Smelyanskiy, V. N., Babbush, R. & Neven, H. Barren plateaus in quantum neural network training landscapes. Nat. Commun. 9, 1 (2018).
Holmes, Z., Sharma, K., Cerezo, M. & Coles, P. J. Connecting ansatz expressibility to gradient magnitudes and barren plateaus. PRX Quantum 3, 010313 (2022).
Marrero, C. O., Kieferová, M. & Wiebe, N. Entanglement-induced barren plateaus. PRX Quantum 2, 040316 (2021).
Patti, T. L., Najafi, K., Gao, X. & Yelin, S. F. Entanglement devised barren plateau mitigation. Phys. Rev. Res. 3, 033090 (2021).
Larocca, M. et al. Diagnosing barren plateaus with tools from quantum optimal control. Quantum 6, 824 (2022).
Friedrich, L. & Maziero, J. Quantum neural network cost function concentration dependency on the parametrization expressivity. Sci. Rep. 13, 9978 (2023).
Sharma, K., Cerezo, M., Cincio, L. & Coles, P. J. Trainability of dissipative perceptron-based quantum neural networks. Phys. Rev.Lett. 128, 180505 (2022).
Kieferova, M., Carlos, O. M., & Wiebe, N. Quantum generative training using rényi divergences. Preprint at arXiv https://doi.org/10.48550/arXiv.2106.09567 (2021).
Pesah, A. et al. Absence of barren plateaus in quantum convolutional neural networks. Phys. Revi. X 11, 041011 (2021).
Lee, J., Magann, A. B., Rabitz, H. A. & Arenz, C. Progress toward favorable landscapes in quantum combinatorial optimization. Phys. Rev. A 104, 032401 (2021).
Martín, E. C., Plekhanov, K. & Lubasch, M. Barren plateaus in quantum tensor network optimization. Quantum 7, 974 (2023).
Grimsley, H. R., Mayhall, N. J., Barron, G. S., Barnes, E. & Economou, S. E. Adaptive, problem-tailored variational quantum eigensolver mitigates rough parameter landscapes and barren plateaus. NPJ Quantum Info. 9, 19 (2023).
Sack, S. H., Medina, R. A., Michailidis, A. A., Kueng, R. & Serbyn, M. Avoiding barren plateaus using classical shadows. PRX Quantum 3, 020365 (2022).
Cerezo, M., Sone, A., Volkoff, T., Cincio, L. & Coles, P. J. Cost function dependent barren plateaus in shallow parametrized quantum circuits. Nat. Commun. 12, 1 (2021).
Uvarov, A. & Biamonte, J. D. On barren plateaus and cost function locality in variational quantum algorithms. J. Phys A Math. Theor. 54, 245301 (2021).
Kashif, M. & Al-Kuwari, S. The impact of cost function globality and locality in hybrid quantum neural networks on nisq devices. Mach. Learn. Sci. Technol. 4, 015004 (2023).
Khatri, S. et al. Quantum-assisted quantum compiling. Quantum 3, 140 (2019).
Uvarov, A., Biamonte, J. D. & Yudin, D. Variational quantum eigensolver for frustrated quantum systems. Phys. Rev. B 102, 075104 (2020).
Leadbeater, C., Sharrock, L., Coyle, B. & Benedetti, M. F-divergences and cost function locality in generative modelling with quantum circuits. Entropy 23, 1281 (2021).
Cerezo, M., Sharma, K., Arrasmith, A. & Coles, P. J. Variational quantum state eigensolver. NPJ Quantum Info. 8, 1 (2022).
Thanaslip, S., Wang, S., Nghiem, N. A., Coles, P. J. & Cerezo, M. Subtleties in the trainability of quantum machine learning models. Quantum Mach. Intell. 5, 21 (2023).
Shaydulin, R. & Wild, S. M. Importance of kernel bandwidth in quantum machine learning. Phys. Rev. A 106, 042407 (2022).
Abbas, A. et al. The power of quantum neural networks. Nat. Comput. Sci. 1, 403 (2021).
Leone, L., Oliviero, S. F. E., Cincio, L. & Cerezo, M. On the practical usefulness of the hardware efficient ansatz. Quantum 8, 1395 (2024).
Holmes, Z. et al. Barren plateaus preclude learning scramblers. Phys. Rev. Lett. 126, 190501 (2021).
Wang, S. et al. Noise-induced barren plateaus in variational quantum algorithms. Nat. Commun. 12, 1 (2021).
Stilck França, D. & Garcia-Patron, R. Limitations of optimization algorithms on noisy quantum devices. Nat. Phys. 17, 1221 (2021).
García-Martín, D., Larocca, M. & Cerezo, M. Effects of noise on the overparametrization of quantum neural networks. Phys. Rev. Research 6, 013295 (2024).
Arrasmith, A., Holmes, Z., Cerezo, M. & Coles, P. J. Equivalence of quantum barren plateaus to cost concentration and narrow gorges. Quantum Sci. Technol. 7, 045015 (2022).
Zeier, R. & Schulte-Herbrüggen, T. Symmetry principles in quantum systems theory. J. Math. Phys. 52, 113510 (2011).
D’Alessandro D. Introduction to Quantum Control and Dynamics Chapman & Hall/CRC Applied Mathematics & Nonlinear Science (Taylor & Francis, 2007).
Zimborás, Z., Zeier, R., Schulte-Herbrüggen, T. & Burgarth, D. Symmetry criteria for quantum simulability of effective interactions. Phys. Rev. A 92, 042309 (2015).
Knapp A. W. Lie Groups Beyond an Introduction Vol. 140 (Springer Science & Business Media, 2013).
Dankert, C., Cleve, R., Emerson, J. & Livine, E. Exact and approximate unitary 2-designs and their application to fidelity estimation. Phys. Rev. A 80, 012304 (2009).
Collins, B., Matsumoto, S. & Novak, J. The weingarten calculus. Amer. Math. Soc. 69, 734 (2022).
Somma, R., Ortiz, G., Barnum, H., Knill, E. & Viola, L. Nature and measure of entanglement in quantum phase transitions. Phys. Rev. A 70, 042311 (2004).
Somma, R. D. Quantum computation, complexity, and many-body physics. Preprint at https://doi.org/10.48550/arXiv.quant-ph/0512209 (2005).
Kökcü, E. et al. Fixed depth hamiltonian simulation via cartan decomposition. Phys. Rev. Lett. 129, 070501 (2022).
Schatzki, L., Larocca, M., Nguyen, Q. T., Sauvage, F. & Cerezo, M. Theoretical guarantees for permutation-equivariant quantum neural networks. npj Quantum Information 10, 12 (2024).
Kazi, S., Larocca, M. & Cerezo, M. On the universality of sn-equivariant k-body gates. New Journal of Physics 26, 053030 (2024).
Wiersema, R., Kökcü, E., Kemper, A. F. & Bakalov, B. N. Classification of dynamical Lie algebras of 2-local spin systems on linear, circular and fully connected topologies. Preprint at arXiv https://doi.org/10.48550/arXiv.2309.05690 (2023).
Barnum, H., Knill, E., Ortiz, G. & Viola, L. Generalizations of entanglement based on coherent states and convex sets. Phys. Rev. A 68, 032308 (2003).
Barnum, H., Knill, E., Ortiz, G., Somma, R. & Viola, L. A subsystem-independent generalization of entanglement. Phys. Rev. Lett. 92, 107902 (2004).
Diaz, N. L., García-Martín, D., Kazi, S., Larocca, M. & Cerezo, M. Showcasing a barren plateau theory beyond the dynamical lie algebra. Preprint at arXiv https://doi.org/10.48550/arXiv.2310.11505 (2023).
Heyraud, V., Li, Z., Donatella, K., Boité, A. L. & Ciuti, C. Efficient estimation of trainability for variational quantum circuits. PRX Quantum 4, 040335 (2023).
Liu, Z., Yu, L.-W., Duan, L.-M. & Deng, D.-L. The presence and absence of barren plateaus in tensor-network based machine learning. Phys. Rev. Lett. 129, 270501 (2022).
Barthel T., & Miao, Q. Absence of barren plateaus and scaling of gradients in the energy optimization of isometric tensor network states. Preprint at arXiv https://doi.org/10.48550/arXiv.2304.00161 (2023).
Miao, Q. & Barthel, T. Isometric tensor network optimization for extensive hamiltonians is free of barren plateaus. Phys. Rev. A 109, L050402 (2024).
Garcia, R. J., Zhao, C., Bu, K. & Jaffe, A. Barren plateaus from learning scramblers with local cost functions. J. High Energy Phys. 2023, 1 (2023).
Letcher, A., Woerner, S. & Zoufal, C. From tight gradient bounds for parameterized quantum circuits to the absence of barren plateaus in qgans. Preprint at arXiv https://doi.org/10.48550/arXiv.2309.12681 (2023).
Arrazola, J. M. et al. Universal quantum circuits for quantum chemistry. Quantum 6, 742 (2022).
Zhang, H.-K., Liu, S. & Zhang, S.-X. Absence of barren plateaus in finite local-depth circuits with long-range entanglement. Phys. Rev. Lett. 132, 150603 (2024).
Napp, J., Quantifying the barren plateau phenomenon for a model of unstructured variational ansätze. Preprint at arXiv https://doi.org/10.48550/arXiv.2203.06174 (2022).
Braccia, P., Bermejo, P., Cincio, L. & Cerezo, M. Computing exact moments of local random quantum circuits via tensor networks. Preprint at arXiv https://doi.org/10.48550/arXiv.2403.01706 (2024).
Hu H.-Y. et al. Demonstration of robust and efficient quantum property learning with shallow shadows. Preprint at arXiv https://doi.org/10.48550/arXiv.2402.17911 (2024).
Zhao, C. & Gao, X.-S. Analyzing the barren plateau phenomenon in training quantum neural networks with the ZX-calculus. Quantum 5, 466 (2021).
Cerezo M. et al. Does provable absence of barren plateaus imply classical simulability? or, why we need to rethink variational quantum computing. Preprint at arXiv https://doi.org/10.48550/arXiv.2312.09121 (2023).
Larocca, M., Ju, N., García-Martín, D., Coles, P. J. & Cerezo, M. Theory of overparametrization in quantum neural networks. Nat. Comput. Sci. 3, 542 (2023).
Marvian, I. Restrictions on realizable unitary operations imposed by symmetry and locality. Nat. Phys. 18, 283 (2022).
Fontana E. et al. Characterizing barren plateaus in quantum ansätze with the adjoint representation. Nat. Commun. https://doi.org/10.1038/s41467-024-49910-w (2024).
Marvian, I. (Non-)universality in symmetric quantum circuits: Why abelian symmetries are special. Preprint at arXiv https://doi.org/10.48550/arXiv.2302.12466 (2023).
Acknowledgements
We thank Zoe Holmes, Mark Wilde, and Akram Touil for fruitful discussions about superoperator norms. We are extremely grateful to Lukasz Cincio for his help with numerical calculations. M.R. and C.O.M. were supported by the Laboratory Directed Research and Development Program and Mathematics for Artificial Reasoning for Scientific Discovery investment at the Pacific Northwest National Laboratory, a multiprogram national laboratory operated by Battelle for the U.S. Department of Energy under Contract DE-AC05- 76RLO1830. B.N.B. was supported in part by a Simons Foundation grant No. 584741. F.S. and M.C. acknowledge support by the Laboratory Directed Research and Development program of Los Alamos National Laboratory (LANL) under project numbers 20230049DR and 20230527ECR. A.F.K. was supported in part by the National Science Foundation under award No. 1818914: PFCQC: STAQ: Software-Tailored Architecture for Quantum co-design and No. 2325080: Software-Tailored Architecture for Quantum Co-Design (STAQ). M.L. was supported by the Center for Nonlinear Studies at LANL. M.C. was initially supported by LANL ASC Beyond Moore’s Law project.
Author information
Authors and Affiliations
Contributions
The project was conceived by B.N.B., C.O.M., M.L., and M.C. Theoretical results were derived by B.N.B., M.R., and M.C., with some independently verified by M.L. and M.C. Numerical simulations were performed by F.S. and M.C. The manuscript was mainly written by M.C., M.R., B.N.B., and A.F.K. All authors contributed to the manuscript review process.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Communications thanks the anonymous reviewer(s) for their contribution to the peer review of this work. A peer review file is available.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Ragone, M., Bakalov, B.N., Sauvage, F. et al. A Lie algebraic theory of barren plateaus for deep parameterized quantum circuits. Nat Commun 15, 7172 (2024). https://doi.org/10.1038/s41467-024-49909-3
Received:
Accepted:
Published:
Version of record:
DOI: https://doi.org/10.1038/s41467-024-49909-3
This article is cited by
-
Adversarial robustness guarantees for quantum classifiers
npj Quantum Information (2026)
-
Variational Quantum Computing for Quantum Simulation: Principles, Implementations, and Challenges
Brazilian Journal of Physics (2026)
-
Experimental demonstration of quantum continual learning with superconducting qubits
npj Quantum Information (2026)
-
Does provable absence of barren plateaus imply classical simulability?
Nature Communications (2025)
-
Variational quantum generative modeling by sampling expectation values of tunable observables
npj Quantum Information (2025)