Introduction

Approximately 50% of the total heat dissipated in industrial processes is low-grade waste heat (< 300 °C), resulting in both energy wastage and environmental pollution. Solid-state thermoelectric (TE) technology, capable of converting waste heat into electricity and vice versa, is believed one of the most promising technologies for utilizing the low-grade waste heat for power generation1,2,3. The energy conversion efficiency of TE materials is mainly gauged by the dimensionless figure of merit, zT = \(\frac{{S}^{2}\sigma }{\kappa }T\), where S, σ, κ, and T are the Seebeck coefficient, electrical conductivity, thermal conductivity, and absolute temperature, respectively4,5,6. A good TE material requires high electrical transports, i.e., large power factors (PF = S2σ), and low thermal conductivity. Over the past a few decades, significant efforts have been dedicated to developing various TE materials from low to high temperatures as well as efficient TE devices7,8,9,10,11,12,13.

It has been widely recognized that the grain boundary (GB) scattering plays a vital role in TE transports, leading to distinct TE properties between single crystals and polycrystals14,15,16,17,18,19,20,21. Owing to the dangling atomic bonding, local off-stoichiometry, and various defects in the GBs, trapping states are formed to capture the charged carriers, leading to much-reduced carrier mobility, electrical conductivity and zT values14. Such phenomenon has been widely observed in many TE materials, including element Te15, SiGe alloys16, PbTe17, SnSe18, Mg2Si19, Half-Heusler20 and Mg3(Bi, Sb)2-based materials21. Therefore, growing single crystals with high TE performance are a long-standing task for device fabrication and industry applications, but it is quite challenging, especially for the growth of large-scale high-quality crystals. In addition, the process of growing single crystals is usually time-consuming and costly, which is also not beneficial for real applications. In contrast, fabricating polycrystals with large grain sizes may push the TE transports to the limit in single crystals and thus provide a simple and cost-effective strategy for large-scale applications. Currently, various approaches have been tried and used for the fabrication of TE polycrystals, such as long-time high-temperature annealing22,23,24, elevating sintering temperature25,26, and adding extra transition metals27,28,29. However, the upper limit of grain sizes by these approaches are usually quite limited, making the TE transports of polycrystals far inferior to those in single crystals. In addition, the content of volatile reactants at high temperatures is also hardly controlled for part of the approaches, leading to the final materials deviating from the target composition. These factors result in the obtained zTs in polycrystals being significantly lower than those of single crystals, especially at room and medium temperatures. Therefore, developing novel strategies to fabricate TE polycrystals with large grain sizes and controllable chemical compositions to realize similar TE performance as that in single crystals is very urgent and challenging for fundamental study and real applications.

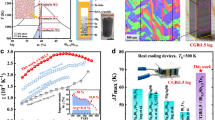
Herein, taking Mg3(Bi, Sb)2-based materials as an example, we develop a liquid-phase sintering strategy to effectively enlarge material’s grain sizes (Fig. 1a) to push the TE performance to the level in single crystals. By introducing the nano-sintering-aid Mg2Cu into GBs during spark plasma sintering process, the average grain size can be improved up to 23.7 μm, resulting in the high carrier mobility and zT values (1.5 at 500 K, Fig. 1b) as well as remarkably high-efficient TE module with an energy conversion efficiency of 7.4% under a temperature difference ΔT of 207 K (Fig. 1c), surpassing all previously reported power generation modules in the same temperature range.

Fig. 1: Nano-sintering-aid at GBs improves TE performance in Mg3(Bi, Sb)2-based materials.
figure 1

a A schematic diagram to fabricate large-grain materials with nano-sintering-aid by liquid-phase sintering. The three dominant stages overlap: grain rearrangement, solution-precipitation, and Ostwald ripening. b Temperature dependent figure of merit zT for Mg3.2Bi1.195Sb0.795Te0.01 – x wt% Mg2Cu with different average grain sizes, in comparison with the reported data of Mg3(Bi, Sb)2-based materials22,24,26,27,30,50,51,52. c Comparison of the measured conversion efficiency among Mg3Sb2-based modules as a function of hot-side temperature Th5,22,25,26,48,53,54. The cold-side temperature Tc is fixed at 288 K. The data of Bi2Te3-based modules are also plotted for comparison55,56. The inset shows the photograph of our TE module.

Full size image

Results

Characterization of the grain phase and grain boundaries

Mg3(Bi, Sb)2 is a typical TE material in which GB scattering of charged carriers significantly restricts the low-temperature electronic transports21. Experimental data have demonstrated that the carrier mobility of Mg3(Bi, Sb)2 could be largely improved by enlarging the grain size21,22,28,29. The zTs at high temperature for Mg3(Bi, Sb)2-based materials have been significantly boosted to 1.7–1.924,29,30,31,32,33, but the value is much low near room temperature or at medium temperatures (0.8–1.3 when temperature is less than 500 K). The usage of sintering-aid during sintering processes can effectively lower the sintering temperature and/or control the grain size34,35. Herein, Mg2Cu was selected as the sintering aid underpinned by a nuanced understanding of its material properties. Firstly, it possesses a melting point of 843 K, which is ideal for facilitating liquid-phase sintering of our Mg3(Sb,Bi)2 materials at 893 K. Secondly, Cu has a very low solubility—potentially being completely insoluble—in Mg3(Sb,Bi)230,36, ensuring that the addition of Mg2Cu will not significantly alter the matrix’s properties. Thirdly, Mg2Cu could potentially compensate for Mg deficiencies at grain boundaries. Therefore, we synthesized nano-Mg2Cu through a ball milling method. The nano-sized Mg2Cu is crucial for the subsequent mixing process, where it can be thoroughly and uniformly mixed with the Mg3Bi1.195Sb0.795Te0.01 matrix. To better control the synthesis process and sample quality, a tantalum-sealing melting technique was adopted to prepare the matrix. Subsequently, the obtained Mg3.2Bi1.195Sb0.795Te0.01 were crushed and mixed homogeneously with x wt% Mg2Cu (x = 0, 2, 3, 5, 7, 10) by low-speed ball milling. Due to its low melting point, most of the Mg2Cu sintering-aid was squeezed out during the sintering process (Supplementary Fig. 1a), leaving only a small amount of nanoscale Mg2Cu residue in the matrix. With the help of sintering-aid, the sintering temperature is reduced to 893 K, which is much lower than the reported values of 973-1073 K25,26,27,33,37. Such a low sintering temperature can greatly reduce the volatilization of Mg to well control material’s compositions. For comparison, a fine-grained Mg3.2Bi1.195Sb0.795Te0.01 sample was also prepared by high-energy ball milling technique. The room temperature powder X-ray diffraction (XRD) measurement for these samples clearly shows that all the diffraction peaks match well with the trigonal structure (space group P\(\bar{3}\)m1) of Mg3Bi2 (Supplementary Fig. 1b). No visible peaks of Mg2Cu are detected due to the limitation of XRD technique. A combination of scanning electron microscopy (SEM), transmission electron microscopy (TEM), and energy dispersive spectrometry (EDS) analysis demonstrates that the residual nano-Mg2Cu is mainly distributed at the GBs (Fig. 2a and Supplementary Fig. 2a). The width of the nano-Mg2Cu ranges from several to tens of nanometers, while the length extends up to micrometers. No signature of Cu is detected in the matrix grains (Supplementary Fig. 2b). These results indicate that the sintering-aid Mg2Cu was liquefied and expelled into the adjacent GBs during the liquid-phase sintering process.

Fig. 2: Morphology of the grain phase and grain boundaries.
figure 2

a High-angle annular dark-field scanning transmission electron microscopy (HAADF-STEM) image with the region containing grain phases and GB phases as well as corresponding energy dispersive spectroscopy (EDS) mapping for the yellow rectangle area. The yellow arrows indicate the nanoscale sintering-aids Mg2Cu. b Reconstructed 3D mappings of Mg, Bi, Sb, Te, and Cu near the GB obtained from atom probe tomography (APT) technique. c One-dimensional concentration profiles of the region of interest (ROI), highlighted by a blue cylinder, along the arrow direction in Fig. 2b. Electron backscatter diffraction (EBSD) images of d Mg3.2Bi1.195Sb0.795Te0.01 sample prepared by ball milling, and (e, f) Mg3.2Bi1.195Sb0.795Te0.01 – x wt% Mg2Cu (x = 0, 5) samples by melting method.

Full size image

We further conducted 3D atom probe tomography (APT) analysis to determine the local chemical compositions and element distributions in both grains and grain boundaries. APT is a cutting-edge technique that enables near-atomic scale elemental mapping with a chemical sensitivity down to tens of parts per million (ppm)28. As shown in Supplementary Fig. 3b, the elements Mg, Bi, Sb, and Te are clearly detected, whereas no trace of Cu is found in the grain phase. This indicates that Cu is nearly insoluble in Mg3(Bi, Sb)2, given the high elemental sensitivity of APT. The elements Mg, Bi, and Sb show distinct oscillations at a sub-nanometer scale in the grain phase, a phenomenon rarely observed before. For the GB phase, the elements Mg and Cu are clearly detected (Fig. 2b), consistent with our EDS results. The size of GB phase, which is mainly the Mg2Cu aid, is about tens of nanometers, and the interface between grain phase and GB phase fluctuates within several nanometers. To provide quantitative information on the composition variation within both grain and GB phases, the region of interest (ROI) is created across these two phases, highlighted by a blue cylinder in Fig. 2b. One-dimensional composition profiles of the ROI along the blue arrow, as displayed in Fig. 2c, clearly show that the detected contents of elements Bi, Sb, and Te gradually decrease when approaching the GB phase, while the element Cu grows out of nothing. The slight Mg deficiency between the grain phase and GB phase aligns with previous observations28,38, which can be traced, in part, to the large potential barrier for electron transports.

Owing to the rapid matter transport in liquids, the coarsening of grains is commonly observed during liquid-phase sintering. The grain size of our samples is measured using electron backscatter diffraction (EBSD) (Fig. 2d–f and Supplementary Fig. 3c). Contrasting with the small average grain size davg of ~1.2 μm observed in the referenced ball milled sample (Fig. 2d), the Mg3.2Bi1.195Sb0.795Te0.01 pellet prepared by our tantalum-sealing melting technique presents a much larger davg of ~7.2 μm (Fig. 2e). Moreover, with the addition of Mg2Cu sintering-aid, the davg is furtherly increased to 23.7 μm with the observed maximum grain size to as large as 60 μm for x = 5 wt% sample (Fig. 2f). However, the davg is decreased to 7.4 μm for x = 10 wt% sample. This indicates that adding appropriate amount of nano-sintering-aid Mg2Cu can promote the growth of grains, whereas excessive nano-sintering-aid Mg2Cu is ineffective. A similar effect has been observed in SiC35, where the average grain size was improved to 10 μm upon the addition of 1 vol% CaO during the sintering process. However, when 3 vol% CaO is added, the average grain size is reduced to 5 μm.

According to Rahaman’s theory obtained in ceramics, the liquid-phase sintering process undergoes three overlapping stages: grain rearrangement, solution-precipitation, and Ostwald ripening39, resulting in noticeable grain growth. Firstly, the low-melting-point Mg2Cu melts and flows towards the adjacent GBs at high temperature and under high pressure, causing residual pores as observed in Fig. 2b. Meanwhile, the liquid sintering-aid forms a thin film around the particles, which acts as a lubricant to lower the interparticle friction and enable the particles to rearrange and coalesce into larger grains. Secondly, the presence of liquid sintering-aids reduces the diffusion barrier for atomic migration, allowing atoms to move quickly from the regions of high curvature (grain boundaries) to that of low curvature (grain interiors) and thus promoting grain growth. Thirdly, the liquid phase can preferentially dissolve smaller particles and redeposit the dissolved material onto larger particles. This process, known as Ostwald ripening, can further facilitate the grain growth. Overall, the appropriate amount of sintering-aid in the sintering process can promote grain growth by enabling particles redistribution, facilitating atomic diffusion, and enhancing Ostwald ripening. However, when an excessive amount of sintering-aid is added, the grains are surrounded by a thick layer of sintering-aid, which hinders grain growth due to the Zener pinning mechanism40.

Characterization and analysis of TE properties

The enlarged grain size and modified GBs have a significantly positive impact on the electrical transports. As shown in Fig. 3a, materials with different grain sizes exhibit distinct temperature dependency of electrical conductivity σ. Above 500 K, all samples have similar σ, while at 5 K, the σ of the course-grained sample, i.e. x = 5 wt% sample, is ten times larger than that of fine-grained ball-milled sample. Attributed to the strong GB scattering to electrons, the σ of the ball-milled sample normally increases with temperature around room temperature, i.e. a positive temperature coefficient of conductivity (TCC). Conversely, the σ of our melted samples shows a negative TCC. The variation of TCC is well consistent with the change in grain size (Fig. 3b). Particularly, the x = 5 wt% sample with the largest grain size shows a T−1.5 temperature dependence that resembles the single-crystal conductivity behavior. This demonstrates that the charge carriers are predominantly scattered by phonons while the GB scattering effect has been largely suppressed.

Fig. 3: Electrical transport properties.
figure 3

Temperature dependent (a) electrical conductivity σ, c carrier concentration n, d carrier mobility μ, f Seebeck coefficient S. The data of ball-milled Mg3.2Bi1.195Sb0.795Te0.01 sample are included for comparison. b Averaged grain size davg and temperature coefficient of conductivity (TCC) y as a function of Mg2Cu content. e Carrier mobility μ as a function of average grain size davg for Mg3.2Bi1.195Sb0.795Te0.01 – x wt% Mg2Cu samples at 5 K and 300 K. The reported data of Mg3(Bi, Sb)2 with similar chemical compositions and carrier concentrations are included for comparison26,30,37,50,57. The dashed lines are derived from a GB-dominated transport model.

Full size image

To better understand the impact of grain size on the electrical transports, we measured the Hall carrier concentration n and carrier mobility μ. All samples, including the ball-milled sample, show a similar n with the values between 4.0 and 4.8 × 1019 cm−3 (Fig. 3c). This indicates that element Cu does not diffuse and enter the crystal lattice of the grains, which is in line with our APT and EDS results. The temperature-dependent carrier mobility μ follows a trend similar to that of σ. Compared to fine-grained samples, the coarse-grained samples clearly exhibit higher carrier mobility, and the difference becomes more pronounced as the temperature decreases (Fig. 3d). The increase in μ is largely due to the suppression of GB scattering. We used a GB-dominated transport model to unveil the relationship between μ and davg at 5 K and 300 K41 (Fig. 3e, calculation details can be found in the Supplementary Information). The experimental data of our melted samples can be well fitted using a potential barrier height Eb of 130 meV. This value is comparable to that (110 meV) of Nb wetted Mg3Sb2 samples28, but lower than the value (170 meV) observed in Mg3Bi1.5Sb0.5 without any GB decoration22. It is recognized that Mg-deficient regions along the GBs are responsible for the increased boundary barrier in n-Mg3(Sb, Bi)238. The barrier height Eb is influenced by a multitude of factors14, including the density of trapping states at the GBs, the concentration of ionized impurity atoms, and the static dielectric constant, among others. In our study, the introduction of the Mg2Cu layer at the GBs signifies a modification of local chemical composition, which potentially leads to changes in the concentration of trapping states and ionized impurities, culminating in a reduced barrier height Eb. The μ of ball-milled samples is below the fitted line, indicating a higher potential barrier in these samples. As the grain size increases, the influence of davg on carrier mobility decreases rapidly before davg = 20 μm at 5 K and 300 K. This is particularly evident in the x = 5 wt% sample, which has an average grain size of 23.7 μm and exhibits a high carrier mobility of 355 cm2 V−1 s−1 at 5 K and 170 cm2 V−1 s-1 at 300 K, approaching the limit of single crystals.

Figure 3f shows the measured Seebeck coefficient S from 2 K to 600 K. Unlike the distinct electrical conductivity σ, all samples exhibit similar S values and a consistent temperature dependency over the entire temperature range. The continuous increase in S with temperature is indicative of a metal-like behavior. Additionally, the experimental S data of all samples align closely with the Pisarenko plot with effective mass m* of 1.15 me, suggesting no obvious change in the conduction band near the Fermi level (Supplementary Fig. 4a). These results confirm that the distinct electron transport properties in our samples are not caused by the carrier concentration and effective mass, but rather by the disparities in grain size. Attributed to the strong electron GB scattering, the room temperature power factor (PF) of ball-milled fine-grained sample is only 11.6 μW cm−1 K−2 (Supplementary Fig. 4b). As grain size increases, the PF is gradually enhanced, especially at low temperatures. A maximum PF of 28 μW cm−1 K−2 is achieved at 300 K in x = 5 wt% sample, which represents 25% and 130% improvements over that of the Mg2Cu-free and ball-milled Mg3(Bi, Sb)2 samples, respectively.

Figure 4a shows the temperature-dependent total thermal conductivity κ. With increasing nano-Mg2Cu content, the κ is roughly decreased mainly because of the reduction from lattice contribution. The slight upturn of κ above 500 K is an indication of the bipolar effect. The lattice thermal conductivity κL is extracted by subtracting the contribution of carriers and bipolar effect from the total thermal conductivity. The calculation details are given in the Supplementary Information. The carrier thermal conductivity κe was calculated based on the Wiedemann−Franz law. The Lorenz factor L was estimated through fitting the Seebeck coefficient to the reduced chemical potential. As shown in Fig. 4b, the room temperature κL (0.94 W m−1 K−1) of the ball-milled sample, even with fined grains, is higher than the value (0.76 W m−1 K−1) of the large-grained melted matrix. This discrepancy can be primarily attributed to the increased oxidation that occurs during the ball-milling process42. The κL of Mg2Cu-containing samples are lower than that of Mg2Cu-free samples, indicating that the Mg2Cu nanoprecipitates, directly observed in Fig. 2, play a vital role in suppressing the heat-carrying phonon propagation even though Mg2Cu itself has a high thermal conductivity. This phenomenon, although counterintuitive, is not without precedent. When the precipitates are present in a low concentration and at the nanoscale, it can effectively scatter phonons and thereby reduce the overall lattice thermal conductivity, as demonstrated in a lot of studies32,43,44.

Fig. 4: Thermal transport properties and zT.
figure 4

Temperature dependent (a) thermal conductivity κ, b lattice thermal conductivity κL, and d zT values for Mg3.2Bi1.195Sb0.795Te0.01 – x wt% Mg2Cu (x = 0, 2, 3, 5, 7, 10). c A comparison of lattice thermal conductivity κL between x = 0% and 5% Mg2Cu samples below 300 K (solid symbols). Calculated κL using the Debye-Callaway model is included to separate the contributions from various phonon scattering mechanisms to the κL. U, PD, B, and NP denote the phonon–phonon Umklapp process, point defect scattering, grain boundary scattering, and nanoprecipitate scattering.

Full size image

An ultralow κL of 0.3 W m−1 K−1 is attained at 600 K in x = 5 wt% sample, which is even lower than the Cahill’s limit and approaches the diffuson limit45,46 (see details in the Supplementary Information). The lattice thermal conductivity is almost independent of the grain size (Supplementary Fig. 5). In comparison to samples with nearly the same chemical composition, the Mg2Cu-containing samples here exhibit lower κL, likely due to the presence of Mg2Cu nanoprecipitates. To elucidate the role of Mg2Cu more clearly, we conducted low-temperature thermal conductivity measurements and employed the Debye-Callaway model for theoretical analysis47 (Fig. 4c and Supplementary Fig. 6), as detailed in the Supplementary Information. Our model takes into account various phonon-scattering mechanisms: the phonon–phonon Umklapp process (U), point defect scattering (PD), grain boundary scattering (B), and nanoprecipitate scattering (NP). The experimental data can be better fitted when the contribution of Mg2Cu nanoprecipitate is factored into the model. This suggests that Mg2Cu nanoprecipitates play a substantial role in reducing the overall lattice thermal conductivity, especially at low temperatures.

Thanks to the remarkably high carrier mobility and ultralow lattice thermal conductivity, exceptional TE performance is realized for Mg3.2Bi1.195Sb0.795Te0.01 – x wt% Mg2Cu. In comparison to the fined-grained samples without nano-sintering-aid Mg2Cu, the large-grained samples exhibit much improved TE figure of merit zT. Specifically, at a temperature of 500 K, the x = 5 wt% sample reached a maximum zT value of 1.5 (Fig. 4d), surpassing the maximum value of 0.8–1.3 for most previously reported Mg3(Bi, Sb)2-based materials at the same temperature (Fig. 1). Moreover, we obtained a superior average zT (zTavg) of 1.25 within the temperature range of 300 K-600 K, ranking among the highest values in near-room-temperature and medium-temperature TE materials (Supplementary Fig. 7). Both high PF and zT suggest that the Mg3(Bi, Sb)2 family holds great promise for applications in the recovery of low-grade waste heat. Additionally, our samples showcase good thermal stability, as evidenced by the repeatable TE properties upon thermal circling (Supplementary Fig. 8).

TE module

We furtherly fabricate an 8-pair TE module by using the n-type Mg3.2Bi1.195Sb0.795Te0.01 – 0.5 wt% Mg2Cu and p-type Bi0.495Cu0.005Sb1.5Te3 materials, see in Fig. 5a. The module fabrication and testing details can be found in the experimental section. The sandwich-structure TE legs, consisting of TE elements and contact layer, are fabricated by the one-step sintering method. Fe and Ni are used as the contact layers for the n-type and p-type materials, respectively. The contact resistivity ρc at the n-type/Fe junction is only 4.5 μΩ cm2 (Fig. 5b), which is significantly lower than the reported ρc in literatures25,26,48, but slightly higher than the value (3.4 μΩ cm2) of Fe foil as the contact layer49. The ρc for the p-type/Ni junction is also as low as 2.3 μΩ cm2, ensuring minimal electrical energy loss at the interface. The measured internal resistance (Rin) and open circuit voltage (Voc) under different hot-side temperatures (Th) are also in line with the predicted values (Supplementary Fig. 9a). The current-dependent output power (P), heat-to-electricity conversion efficiency (η), load voltage (V), and heat flow (Q) of the module under a series of Th are plotted in Fig. 5c, d, Supplementary Fig. 9b, and Supplementary Fig. 10. With increasing current, The P initially increases and then reaches a maximum value when the resistance of external electrical load is equal to Rin of the module. A maximum P of ~ 0.3 W and a conversion efficiency η of 7.4% is achieved when the hot-side temperature is 495 K and ΔT is 207 K, surpassing all previously reported power generation modules in the same temperature range (Fig. 1c). Because the TE performance of the p-type partner is much lower than the n-type partner above 350 K (Supplementary Fig. 11), the prominent module performance is mainly contributed by our n-type materials.

Fig. 5: Performance of the TE module comprised of n-type Mg3.2Bi1.195Sb0.795Te0.01 – 0.5 wt% Mg2Cu and p-type Bi0.495Cu0.005Sb1.5Te3.
figure 5

a Schematic diagram of the 8-pair TE module. b Contact resistivities for the n-type/Fe junction and p-type/Ni junction. Current (I) dependence of (c) output power and d conversion efficiency.

Full size image

Discussion

In summary, we have successfully enlarged the grain sizes and then pushed the electrical properties and TE performance of Mg3(Bi,Sb)-based polycrystals to the limit in single crystals by introducing Mg2Cu nano-sintering-aid at GBs. Exceptional TE figure of merit and high efficiency TE module are realized near room temperature and at medium temperature, both of which are much superior to the literatures. This work provides an in-depth, cheap, and simple strategy for the fabrication of high-performance TE polycrystals for large scale applications.

Methods

Tantalum-sealing melting technique

A tantalum-sealing melting technique was adopted to synthesize coarse grain polycrystalline Mg3.2Bi1.195Sb0.795Te0.01. Stoichiometric Mg (magnesium slug, 99.95%, Alfa Aesar), Bi (bismuth shot, 99.999%, Aladdin), Sb (antimony shot, 99.999%, Alfa Aesar), and Te (Tellurium shot, 99.9999%, Alfa Aesar) were weighed out and loaded into tantalum tube in the Ar-filled glovebox. Herein, an excess Mg of ~7% was used to compensate for the Mg deficiency along the grain boundary and the mass loss due to its high chemical activity. An arc melting furnace is used to seal the tantalum tube under Ar atmosphere. The obtained tantalum tube was put into a sealed quartz tubes under vacuum, which was heated to 1373 K in 11 h and held at this temperature for 24 h, then naturally cooled to room temperature. The prepared ingot was crushed using an agate mortar in the glovebox.

Liquid-phase sintering process

For the synthesis of sintering aid Mg2Cu, Mg powder (99.99%, Aladdin) and Cu powder (99.9%, Alfa Aesar) were weighted out in the stoichiometric ratio of Mg2Cu and put into a stainless-steel vessel in the glovebox. The nano-Mg2Cu powder was obtained by a high-energy mill (MSK-SFM-3-1, Hefei Kejing Materials Technology Co. Ltd.) at 1500 rpm for 12 h. A series of Mg3.2Bi1.195Sb0.795Te0.01 – x wt% Mg2Cu (x = 2, 3, 5, 7, 10) composites were prepared by mixing the Mg3.2Bi1.195Sb0.795Te0.01 powder with nano-Mg2Cu powder using a low-speed ball milling for 10 min. For control purpose, the Mg3.2Bi1.195Sb0.795Te0.01 powder without Mg2Cu was treated with the same process. The resultant mixtures were loaded into graphite dies and sintered using a spark plasma sintering system (SPS-222H, Fuji Electronic Industry Co. Ltd) at 893 K under an axial compressive stress of 50 MPa for 6 min. All the samples remain robust, with relative density exceeding 98% (Supplementary Table 1).

Ball milling

For reference, a fine-grained Mg3.2Bi1.195Sb0.795Te0.01 sample was prepared by high energy ball milling technique. High purity Mg (magnesium powder, 99.95%, Alfa Aesar), Bi (bismuth shot, 99.999%, Aladdin), Sb (antimony shot, 99.999%, Alfa Aesar), and Te (Tellurium shot, 99.9999%, Alfa Aesar) were loaded in a stainless-steel vessel in the glovebox. Then the stainless-steel vessel undergoes a mechanical alloying process by a high-energy mill (MSK-SFM-3-1, Hefei Kejing Materials Technology Co. Ltd.) at 1500 rpm for 6 h. The obtained Mg3.2Bi1.195Sb0.795Te0.01 powder was densified by a SPS system with the same condition of melting samples.

TE module fabrication

An 8-pair TE module comprised of n-type Mg3.2Bi1.195Sb0.795Te0.01 – 0.5 wt% Mg2Cu and p-type Bi0.495Cu0.005Sb1.5Te3 materials was successfully fabricated. The stoichiometric of Bi (bismuth shot, 99.999%, Aladdin), Sb (antimony shot, 99.999%, Alfa Aesar), Te (Tellurium shot, 99.9999%, Alfa Aesar), and Cu (shot, 99.999%, Alfa Aesar) were weighed into sealed quartz tubes according to the atomic ratio of Bi0.495Cu0.005Sb1.5Te3 and then held at 1373 K for 12 h before quenching into water. The obtained ingot was annealed at 673 K for 5d and then hand ground to fine powder. The densification process was accomplished by spark plasma sintering system (SPS-222H, Fuji Electronic Industry Co. Ltd) at 683 K under an axial compressive stress of 50 MPa for 10 min. TE legs of module with interfacial layer is fabricated by the one-step sintering method and the Fe powder and Ni powder are chosen as the interfacial materials for n-type Mg3.2Bi1.195Sb0.795Te0.01 – 5 wt% Mg2Cu and p-type Bi0.495Cu0.005Sb1.5Te3 legs, respectively. In order to reduce the thermal resistance, we use super-high thermal conductivity aluminum nitride ceramics as the electrically isolated substrates at both the hot-side and cold-side (Fig. 5a). Based on the very analogous electrical and thermal transport properties (Supplementary Fig. 11), we determine that the cross-sectional area Ap of p-type legs is equal to that (An) of the n-type legs (Ap/An = 1). A longer leg length will produce a larger effective temperature difference across the TE module due to a smaller proportion of energy dissipation at the interface, which enables a higher conversion efficiency but a lower power output density. Meanwhile, the height of the module element can influence the fabrication process and cost. Longer and thinner modules are more difficult to fabricate with consistent quality. Herein, the length of the TE legs is decided to be 5 mm for balancing the maximum power generation performance and convenience of processing. Undergoing dicing, grinding, and polishing, the n-type and p-type TE legs are processed into 1.8 × 1.8 × 5 mm3 pieces. The lengths of the interfacial layer and thermoelectric elements are 0.5 mm and 4 mm, respectively. These 8-pair TE legs and copper electrodes were joined with Sn90Sb10 brazing material while the copper electrodes were connected to aluminum nitride ceramic with silver paste. Four copper wires were soldered to the cold-side electrodes for current and voltage measurements.

Material and module characterization

Room-temperature powder X-ray diffraction data were measured in a Bruker D8 Advance diffractometer to characterize the phases. A field emission scanning electron microscopy (FESEM, Tescan Mira3, Czech Republic) equipped with energy dispersive X-ray spectroscopy (EDS, Oxford, UK) was applied to observe the chemical compositions. The morphology of our samples was performed by a Talos F200X G2 field emission transmission electron microscope. Atom-probe tomography (APT) analysis was performed in a Cameca Instruments (LEAP 5000 XR) by applying a DC voltage of 2–4 kV and a laser pulse energy of 3 pJ. The needled-sharped samples for the APT analysis were prepared through the standard lift-out procedure using a focused ion beam (Helios, Nanolab 600). The electrical conductivity (σ) and the Seebeck coefficient (S) were measured using ZEM-3 (ULVAC Co. Ltd) under a helium atmosphere. The total thermal conductivity (κ) was calculated with the formula κ = ρCpD. The thermal diffusivity (D) was measured by a commercial laser flash device (LFA 457, Netzsch Co. Ltd). The density ρ was measured based on the Archimedes principle and the heat capacity Cp was estimated via the Dulong–Petit law. The electrical conductivity and Hall coefficient were measured by a physical property measurement system (PPMS-9, Quantum Design). Hall coefficient was using the Hall-bar method under a ± 3 T magnetic induction from 5 K to 300 K.

The power generation performance was measured using a home-made test system in Shanghai Institute of Ceramics, which offers precise temperature regulation, being crucial for accurate measurement of TE performance, especially under the fluctuating conditions of the hot-side temperature. A block of Cu, endowed with thermal conductivity of κCu, was utilized to serve as the heat flow meter. A custom-made heater, which is capable of operating at temperatures up to 900 K, was deployed to function as the heat exchanger. Our TE module was positioned between the Cu block and the heater, facilitating optimal thermal interaction. The power source and data acquisition process were managed through the LabView software. An external direct current electrical was loaded to the module, enabling the generation of voltage (V) and current (I) and the subsequent calculation of power output (P = VI). Then, the heat flow (Q) can be obtained based on the one-dimensional Fourier’s law:

$$Q={A}_{{{{\rm{C}}}}{{{\rm{u}}}}*\kappa {{{\rm{C}}}}{{{\rm{u}}}}*}\varDelta T/L$$
(1)

where Acu is the cross-sectional area of the Cu block, ΔT is the temperature difference measured by the thermocouples embedded in the Cu block, and L is their vertical distance. The TE conversion efficiency η was calculated using the following equation:

$$\eta=\frac{P}{P+Q}\times 100\%$$
(2)

The cold-side temperature was maintained at 288 K, while the hot-side temperature was varied from 323 K to 498 K.