Introduction

Biological ion channels usually present a high flux of 107 ~ 108 ions∙s−1 and a high ion selectivity1,2,3,4,5,6, and malfunctioning ion channels can cause a wide variety of disorders, including neurological, cardiac and skeletal muscle diseases7. Understanding of ion channel transport will be important for the question of how our life achieves ultralow energy consumption in the information transmission, energy conversion and biosynthesis8. Inspired by the biological channels, a large number of artificial membranes with nanopores have been developed that achieve ion transport with a high flux (~108 ions·s−1), high selectivity, and even ultralow resistance9,10,11,12,13,14,15,16. Although the high selectivity of ion channels has already been well studied17,18,19,20, the mechanism underlying the high flux and ultralow energy consumption is still lacking. Recent progress has shown that the ion current of biological channels is obviously different from that of classical Newton’s fluid. In 2016, based on two-dimensional infrared spectra of semisynthetic KcsA channels, a knock-on model was proposed for K+ ion permeation through the channel21. In this model, K+ ions alternating with water molecules collectively move through the filter when a new K+ enters the ion-selective filter. After that, molecular dynamics (MD) simulations of the Streptomyces lividans KcsA channel suggested a direct knock-on model for K+ ion transport, where dehydrated ions occupy all the binding sites of the filter without water molecules22. Moreover, polarizable MD simulations showed that the configuration of the four ions in the KcsA filter is thermodynamically stable under charge transfer23,24,25. Very recently, the study of a one-dimensional lattice model theoretically predicted that there is a quantum coherent ion state of KcsA channels, which can carry neural information26. Despite their difference, the new developments indicate the collective and ordered behavior of confined ions in biological channels, which provides a potential way to understand the energy-efficient high-flux ion transport of channels.

In this study, through molecular dynamics simulations and multitimescale fine analyses, we demonstrate that coherent ion oscillation and coherent ion transfer occur in the KcsA potassium channel, which together determine transport. The coherent oscillation state of K+ ions confined in the channel, remaining 103 ps, dominates each transport event, serving as the basis for the high flux of ~108 ions∙s−1. The coherent transfer of confined ions is a superfast process of several picoseconds without perturbation effect on the coherence, acting as the directional key of transport. An increase in ion coherence can significantly enhance the ion conductance and thus transport efficiency. Further analyses based on the de Broglie wave of ions indicate that such coherence is allowed by quantum mechanics.

Results and discussion

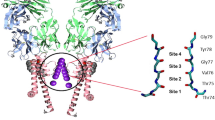
First, to include information on the transport dynamics of the KcsA potassium channel, we introduced a new region beyond the ion-selective filter, based on the ion distribution under a transmembrane voltage, named Filter+ (Fig. 1a). A model of the open-state KcsA channel (PDB IDs: 1K4C for the ion-selective filter and 3F5W for others22,27,28) was applied in our MD simulations, enveloped by a phospholipid bilayer membrane (Fig. 1a left; the whole simulation system is shown in Supplementary Fig. 1). According to protein structure, the channel is usually divided into three regions: the extracellular loop, ion-selective filter, and cavity29. To determine characteristics of the transported ions, we performed ion distribution analyses under different transmembrane voltages (V). As shown in Fig. 1a right, when V = 0, there were four sites (i.e., S1, S2, S3 and S4) for ions in the filter area, consistent with previous experiments and simulations23,27,28. When the voltage increased from 0 mV to 100 mV, site S4 shifted from the filter to the cavity, and the changes in the other three sites were very slight, which indicates that the distribution of ions in the area below S3 strongly depends on the transmembrane voltage, and thus is closely related to transport dynamics. In addition, a minor voltage-dependent peak of distribution was also observed in the area of KcsA extracellular loops, as labeled S1’. At V = 100 mV, the occurrence probabilities of ions at sites S1 + S1’, S2, S3 and S4 were 77%, 100%, 99% and 44%, respectively (Supplementary Figs. 1, 2). Hence, the Filter+ region, composed of KcsA filter with parts of the cavity and extracellular loops, can cover the distribution peaks S1’, S1, S2, S3 and S4 of the confined ions under a transmembrane voltage, which involves ion transport dynamics information of the KcsA channel.

Fig. 1: Ion coherence in the transport dynamics of the KcsA channel.
figure 1

a Transmembrane voltage dependence of the K+ ion distribution. Left: Simulation system of the KcsA channel. The KcsA protein (cyan) is embedded in a phospholipid bilayer membrane (green) in the presence of solution molecules (gray). Middle and right: Transmembrane voltage (V) dependence of the K+ ion distribution. The Filter+ region is introduced for covering the S1’, S1, S2, S3 and S4 peaks at a voltage of V = 100 mV. b Typical picosecond-scale z-coordinate trajectories of confined K+ ion oscillation and an ion moving out of the channel at the transmembrane voltage of 100 mV. The black, red, green and blue curves indicate the trajectories of the K1, K2, K3 and K4 ions, respectively. Top: Oscillation waveforms of confined ions in Filter+ along the channel axis. The peak locations (solid gray lines) per oscillating trajectory are almost the same as those of other trajectories, and a similar case also occurs in the trough locations (dotted gray lines), indicating that the oscillation phases of confined K+ ions match each other, i.e., coherent oscillation. Bottom: Ion transfer trajectories. The four ions simultaneously move up of ~2 Å during δ = 0 ps to 7 ps, the ions K1 and K4 separately move up ~2 Å during δ = 118 ps to 177 ps, and the K1 ion moves out of channel after δ = 177 ps. c Multitimescale evolution of the coherence-associated ion transport dynamics of the KcsA channel. Top: Typical picosecond-scale trajectory of the ion coherence degree αF+. Middle and bottom: Typical nanosecond- (middle) and microsecond- (bottom) scale trajectories of the ion coherence degree (black) and transport events (red). The dashed green line represents the time location of transport event occurrence. The green curve denotes the distribution probability of αF+, which has two peaks at 0.267 and 0.141, respectively, indicating two kinds of coherence states for the ions confined in the KcsA Filter + .

Full size image

To determine the ion coherence in KcsA transport dynamics, we carried out picosecond-scale analyses on the coordinate trajectories of the confined ions in Filter+ along the KcsA channel axis. The trajectories under a transmembrane voltage V = 100 mV are shown in Fig. 1b, with the K+ ions labeled K1, K2, K3 and K4. From δ = –220 ps to 0 ps, the four trajectories evolved along four parallel lines, indicating that the ions oscillate in their respective confinement sites of Filter + . As shown in zoom-in I of Fig. 1b, the peak locations of an oscillating trajectory were almost the same as those of other trajectories, and a similar case was also observed in the trough locations. The oscillation trajectories thus had an identical phase of oscillation, meaning that the confined ions coherently oscillate together, consistent with the coherence state expected by the one-dimensional lattice model26. From 0 ps to 7 ps, the z-coordinates of four ions simultaneously shifted up ~2 Å, suggesting that collective and superfast ion transfer takes place (Movie 1). After that and before δ = 118 ps, the four trajectories continued to evolve along four parallel lines, and their oscillation waveforms matched each other (see the locations of the peaks and troughs in zoom-in II of Fig. 1b), indicating that the oscillation coherence of the four ions remains. From 118 ps to 177 ps (Δt = 59 ps), the ions K1 and K4 separately moved up ~2 Å (Movie 2), different from the collective ion transfer above. Finally, the K1 ion moved out of Filter + , and the other ions underwent coherent oscillation in the channel (zoom-in III of Fig. 1b). In addition, the charge transfer between filter-confined K+ ion and filter is estimated to only have a weak effect on the Coulombe attraction between the ion and the carbonyl oxygen on the filter wall, and thus only a weak perturbation on the ion coherence (Supplementary Fig. 3, more discussions in Supplementary Information Section 1). Meanwhile, as the confined ions crossed the barrier between two sites of the filter, the dynamical change of charge per ion was ~0.05 e, which indicates that the dynamical charge change occurring in the superfast process of ions moving is very slight. Hence, we can conclude that there exists ion coherence in KcsA transport.

To study the relationship between ion coherence and transport dynamics of the KcsA channel, we conducted coherence-degree analyses on K+ ion transport dynamics. Based on the KcsA Filter + , an ion coherence order degree αF+ was introduced as follows:

$${\alpha }_{{{{\rm{F}}}}+}(t)={A}_{N}{{\sum}_{i < j}^{N}}f\left({{v}^{ \rightharpoonup }}_{{ij}}\right),$$
(1)

with

$$f\left({{v}^{ \rightharpoonup }}_{{ij}}\right)=1-\frac{\left|{{v}^{ \rightharpoonup }}_{i}-{{v}^{ \rightharpoonup }}_{j}\right|}{\left|{{v}^{ \rightharpoonup }}_{i}\right|+\left|{{v}^{ \rightharpoonup }}_{j}\right|},$$
(2)

where \({{v}^{ \rightharpoonup }}_{i}\) and \({{v}^{ \rightharpoonup }}_{j}\) indicate the velocities of the i-th and j-th transporting K+ ions, respectively, while \({A}_{N}=1/C(2,N)\) denotes the normalization constant of αF+, with N = 4. The degrees αF+ = 1 and 0 indicate full and no coherence, respectively. Although three- and four-ion occupation dominated the ion configuration of Filter+ in the transport process under a transmembrane voltage (Supplementary Fig. 2b), we still fixed N at 4 in the αF+ calculations. The three-ion configuration of Filter+ can be regarded as the case that there are still four ions taking part in a transport event, where three ions occupy Filter+ and one ion incoherently moves in water. As the picosecond-scale trajectory shown in Fig. 1c top, two plateaus of coherence degree αF+(t) were observed with average \({\bar{\alpha }}_{{{{\rm{F}}}}+}\) = 0.281 and 0.140 over the time of their respective plateaus, and the transition between them started at δ = 118 ps and took 59 ps. This result suggests that there are two coherence states of transported ions in the channel. A comparison with the ion coordinate trajectories shown in Fig. 1b indicates that from δ = 0 ps to 7 ps the collective and superfast ion transfer does not perturb coherence, i.e., a coherent transfer of ions occurs. Moreover, the transition from higher to lower coherence states during 118 ps to 177 ps can be attributed to the disordered transfer of K1 and K4 ions, as is clearly different from the effect above of coherent ion transfer. The correlation of coherent ion transfer and ion permeation events in the entire simulation was 98.1% (Supplementary Fig. 4), indicating that coherent ion transfer is a key to transport directionality. In the nanosecond- and microsecond-scale trajectories (Fig. 1c middle and bottom), the case of αF+ → 0 was not observed, suggesting that ion coherence cannot be ignored in all K+ permeation events. The coherence degree repeatedly switched between the higher and lower plateaus, which leads to two distribution peaks of αF+ at 0.267 and 0.141, respectively (Fig. 1c bottom), further indicating two kinds of ion coherence states in KcsA transport. The average lifetime of higher coherence states (i.e., the duration of plateaus) was 4.9 ± 4.4 ns and that of lower coherence states was 7.5 ± 6.0 ns, while the maxima were sharply located at 1.7 ns and 2.7 ns, respectively (Fig. 2a). The large error in the coherence state lifetime was caused by its non-normal distribution. The fractions of the system in higher and lower coherence states of overall time were 0.38 ± 0.07 and 0.58 ± 0.07, respectively (Fig. 2b). There thus exist the coherent states of KcsA-confined ions with a nanosecond-level lifetime. The permeation trajectory was discontinuous and quasi-continuous at the nanosecond and microsecond scales, respectively, consistent with the direct knock-on model (Fig. 1c bottom)22. The average flux was 5.9 ± 0.2 107∙ions∙s−1, agreeing with the experimental results of 107 to 108 ions∙s−11,2. The probability of a higher ion coherence state occurring within 100 ps before the permeation step was 98.1% (Fig. 2c), indicating that such a coherence state is necessary for transport. The average time per ion transport (i.e., one over flux) was 16.9 ns, comparable to the sum (12.4 ns) over the average lifetimes above of higher and lower coherence states, denoting that the high flux is closely related to the coherence states. Hence, we can conclude that the coherent ion oscillation state of nanosecond-level lifetime in KcsA Filter+ dominates each transport event, and the superfast coherent ion transfer of several picoseconds without perturbation of the ion coherence acts as the directional key of transport, which together leads to the high-flux transport of the KcsA channel.

Fig. 2: Ion coherent state analyses at the transmembrane voltage of 100 mV.
figure 2

a Non-normal distribution of coherent state lifetime (i.e., duration). b Occurrence probabilities of higher- and lower-coherence states of the overall time. Data are presented as mean ± SD with n = 4 samples. c Probability of a higher coherence state occurring before an ion permeation event. The label δ (<ΔtN) indicates the time region of counting the higher coherence state advanced to an ion permeation event, and ΔtN (~103 ps) denotes the time interval between the N and N + 1 ion permeation events.

Full size image

To explore the effect of ion coherence on the intrinsic property of channel (e.g., conductance that is usually used to describe the transport efficiency), we further introduced a KcsA intrinsic ion coherence degree (αF) that is independent of the transmembrane voltage (V) and flux (F). The αF of the KcsA protein was defined based on the KcsA filter (but not Filter + ) as follows:

$${\alpha }_{{{{\rm{F}}}}}(t)={B}_{n}{{\sum}_{i < j}^{n}}f\left({{v}^{ \rightharpoonup }}_{{ij}}\right),$$
(3)

where the normalization constant \({B}_{n}=1/C(2,n)\), and n indicates the number of K+ ions indeed confined in the KcsA filter. This degree would have a property different from the previous coherence degree αF+ due to the different definition domains and different normalization constants. To validate the independence of αF on the transmembrane voltage, we compared the trajectories at V = 100 mV and 0 mV. The coherence degree αF with the voltage of 100 mV remained at the level with an average value of \({\bar{\alpha }}_{{{{\rm{F}}}}}\) = 0.279, and that without the voltage at the level of 0.278, which agreed well with each other (Fig. 3a), clearly different from the Filter + -based degree αF+ that repeatedly switched between the levels of 0.267 and 0.141 (Fig. 1c). The fluxes at 100 mV and 0 mV were 5.95 × 107 ions∙s−1 and vanishing, respectively. Therefore, αF is a variable independent of transmembrane voltage and flux, and then the average value \({\bar{\alpha }}_{{{{\rm{F}}}}}\) can be taken as an order parameter to describe the intrinsic ion coherence of the KcsA protein.

Fig. 3: Ion coherence effect on the conductance of the KcsA channel.
figure 3

a Intrinsic ion coherence degree αF of the KcsA protein independent of transmembrane voltage V and flux. Upper and lower panels: Typical trajectories of αF with and without the voltage, respectively. b–d Resonant regulation of intrinsic KcsA ion coherence by an electromagnetic wave (EMW). Data are presented as mean ± SD with n = 4 samples. b Vibration spectra of K+ ions confined in the filter along the directions parallel (red) and perpendicular (green) to the channel axis (z axis). c Regulated coherence order parameter \({\bar{\alpha }}_{{{{\rm{F}}}}}\) (black) of the KcsA protein by the EMW with a frequency ν = 2.4 THz. The chartreuse curve indicates the system temperature in the presence of the EMW. d Frequency dependence of the regulation. e Ion coherence effect on KcsA conductance (black) and disordered transport-invalid event probability P− (light blue). Data are presented as mean ± SD with n = 4 samples. Insert: An invalid event of transport, i.e., the filter-confined K+ ion moves back to the cavity.

Full size image

With the help of the KcsA intrinsic ion coherence order parameter \({\bar{\alpha }}_{{{{\rm{F}}}}}\), we studied the effect of ion coherence on the intrinsic property of KcsA conductance. Firstly, to regulate the ion coherence \({\bar{\alpha }}_{{{{\rm{F}}}}}\) of the KcsA protein, an electromagnetic wave (EMW) with a specific frequency was added to the simulation system. Vibration spectrum analyses of the filter-confined K+ ions were performed to determine the frequency of EMW30. The characteristic peak of ion vibration parallel to the channel axis located at 2.4 THz (Fig. 3b), which was applied to resonantly regulate the transport-associated ion coherence. As shown in Fig. 3c, the intrinsic coherence order parameter \({\bar{\alpha }}_{{{{\rm{F}}}}}\) of the KcsA protein nonlinearly increased from 0.279 ± 0.0004 to 0.290 ± 0.002 as the 2.4-THz EMW strength increased from 0.0 V∙nm−1 to 0.4 V∙nm−1. Note: the strength effect of terahertz EMWs including far infrared light on a biological system is still required to explore, as is already beyond this study (more discussions in Supplementary Information Section 2). The system temperature remained at 310.00 ± 0.03 K (i.e., 36.85 ± 0.03 °C) with the increase of EMW strength, indicating that the heating effect of EMW can be ignored (the effects of EMW on the kinetic energy of the confined ion is shown in Supplementary Fig. 5, Supplementary Information Section 3). To study the frequency dependence of EMW regulation, we applied typical frequencies of 0.02 THz, 10 THz and 30 THz as comparisons (Supplementary Fig. 6). The 0.4 V∙nm−1 EMWs with these frequencies had only a weak influence on \({\bar{\alpha }}_{{{{\rm{F}}}}}\), clearly different from the effect of the 2.4-THz EMW (Fig. 3d, also Supplementary Fig. 7 without the EMW effect on water). Therefore, the 2.4-THz EMW can resonantly regulate the ion coherence of KcsA protein. Next, the ion conductance (G) was calculated by the equation G = qF/V, where the voltage V was set at 100 mV in the simulations, q (= 1 e) and F indicate the K+ ion charge and flux, respectively. Energy dissipation of the ion current then can be estimated to be proportional to 1/G. As the ion coherence increased from 0.280 to 0.290, the conductance of channel increased from ~6 × 108 e ∙ s−1 ∙ V−1 to ~19 × 108 e ∙ s−1 ∙ V−1 (Fig. 3e), which will cause the increase of ion flux at any fixed voltage. Therefore, the ion coherence can effectively enhance the KcsA conductance and then reduce the energy consumption of ion transport.

To reveal the mechanism underlying the coherence-caused enhancement of the conductance, we explored the effect of KcsA ion coherence on the probability (P − ) of disordered transport-invalid events (i.e., the filter-confined ion moves back to the cavity, Supplementary Fig. 8, Movies 3 & 4). As shown in Fig. 3e, P- was ~28% for \({\bar{\alpha }}_{{{{\rm{F}}}}}\) < 0.280 and only ~8% for \({\bar{\alpha }}_{{{{\rm{F}}}}}\) > 0.284, with a transition connecting them. The ion coherence thus can microscopically suppress the disordered invalid events of transport, causing the enhancement of KcsA conductance.

Besides the applied frequency of 2.4 THz above, the frequency of 53.7 THz can also be used to regulate the KcsA ion coherence and conductance. As shown in Supplementary Fig. 9a, there is a Coulomb coupling between the filter-confined K+ ions and the negatively charged oxygen atoms of C = O bonds on the filter wall, which will cause a strong correlation between them26. Our spectrum analyses on the ion-included selectivity filter of KcsA channel showed that the C = O bonds had a stretching vibration at 53.7 THz, while the filter-confined ions had an oscillation frequency at 2.4 THz (Supplementary Fig. 6). Therefore, the 53.7-THz EMW can resonantly regulate coherence of the oscillations of filter-wall C = O bonds, affecting the K+ ion coherence and transport properties (e.g., conductance, flux) with help of the coupling above (Supplementary Fig. 9b, c), like the effect of 2.4-THz EMW (more details in Supplementary Information Section 4). In fact, it has been reported experimentally that the 53.7-THz EMW nonthermally and resonantly enhances the K+ ion current through potassium channels of neuronal action potentials31 and accelerates associative learning32.

To explore the quantum mechanics validity of the KcsA coherent transport, we performed analyses on the de Broglie wavelength of filter-confined ions. Based on our simulations, the de Broglie wavelength was estimated to be in the range of 1 ~ 10 Å, which was consistent with the wavelength of predicted quantum state theoretically based on a one-dimensional lattice model of the K+ ion channel26. This scale was of the same order of magnitude as the dimension (~9 Å, Supplementary Fig. 9a) of three consecutive sites in the filter, and significantly larger than the wavelength (<0.5 Å) of a free ion at the temperature of 310 K33. The ion coherence is thus allowed by quantum mechanics, and then the confined ions moving as a quantum coherent body is possible, which is required to further explore in future.

Finally, we used a schematic representation to clearly present the coherence-determined ion transport of the KcsA channel (Fig. 4). In the initial state of a nanosecond-level transport event, three confined K+ ions (K1, K2, K3) coherently oscillate in the KcsA filter, and one K+ ion (K4) performs motion in the cavity (Fig. 4 top left). Three steps are conducted for coherent ion transport. In step I, the ion K4 enters the filter and coherently oscillates with the ions K1, K2 and K3, which takes ~50 ps. For step II, the four confined ions in Filter+ maintain the collective coherent oscillation for ~103 ps, during which these ions take ~7 ps to perform a coherent transfer that is a superfast process (Proc + ) without perturbation effect on the ion coherence, acting as a key to transport irreversibility. Finally, in step III of ~60 ps, the ion K1 leaves the Filter+ for the extracellular region and becomes incoherent from the coherent ions K2, K3 and K4, i.e., a coherent ion transport event of the KcsA channel is achieved. In addition, there is an alternative process (Proc–) instead of the transport key Proc+ (Fig. 4 bottom). Namely, the filter-confined ion K4 carries out a decoherence process (~30 ps) of moving back to the cavity as a transport-invalid event, which can be suppressed by increased ion coherence through a coherence-induced transition. The probability P– of Proc– is very small when the coherence is greater than a critical value, which can cause a large increase in the ion flux of the KcsA channel.

Fig. 4: A summary of ion coherence-determined transport through the KcsA channel.
figure 4

Initially, the confined K+ ions (K1, K2, K3) in the filter coherently oscillate together, with the help of ion-ion coupling caused by the negatively charged O atoms of C-O bonds on the wall of the filter. Meanwhile, one K+ ion (K4) performs free motion in the cavity. Top: Three steps of coherent ion transport. Step I: The K4 ion enters the filter and coherently oscillates with the ions K1, K2 and K3. Step II: The four confined ions in Filter+ coherently oscillate together, during which the ions undergo a coherent ion transfer (labeled Proc + ) as the directional key of transport. P+ indicates the probability of Proc + . Step III: The ion K1 moves out of the Filter+ and becomes incoherent from the coherent ions K2, K3 and K4. Bottom: An alternative process (Proc–) instead of Proc+ in step II, i.e., the ion K4 moves back to the cavity. An increase in the KcsA ion coherence \({\bar{\alpha }}_{{{{\rm{F}}}}}\) can cause a clear decrease in the probability P– of Proc– at a critical value of coherence, i.e., a coherence-induced transition, leading to a large increase in ion flux. The dashed orange and blue lines indicate the maximum probability locations of KcsA-confined ions and the terminus of the KcsA Filter + , respectively.

Full size image

In summary, by analyzing the multitimescale fine dynamics of confined K+ ions in KcsA channel, we demonstrated that ion coherence occurs in the biological channel, which determines transport. The coherent oscillation state of ions confined in the KcsA Filter+ as the physical basis of high flux dominates each of transport events, the superfast coherent ion transfer without perturbation effect on the ion coherence acts as the directional key of transport, which together leads to a current of ~108 ions∙s−1 in the KcsA channel. An increase in the ion coherence can effectively enhance the ion conductance and thus current, through a coherence-induced transition in disordered invalid transport events. The analyses of de Broglie wave indicate that such coherence is allowed by quantum mechanics. Our results provide an explanation from the perspective of ion coherence for the high-flux ion transport with ultralow energy consumption of biological channels. The findings will improve the understanding of the physics of energy-efficient ion transport in biological systems, potentially promoting developments in treatment strategies for ion channel-associated diseases and health problems, and even in design of bio-inspired materials and devices with ultralow energy consumption.

Methods

System preparation

We generated an open-state model of the KcsA channel employing the methodology outlined by Köpfer et al.22,34. Specifically, A high-resolution protein (PDB code: 1K4C27) was applied for the ion-selective filter and a low-resolution protein (PDB code: 3F5W28) in open state for the other parts (Supplementary Fig. 1). This approach was necessitated by the dearth of high-resolution (≤2 Å) structures depicting the open state of K+ ion-selective channel protein KcsA, despite the repository containing more than 100 crystallographic entries. The whole protein channel conformation was sufficiently optimized. The advanced Propka tool35 was used to predict the protein protonation state under a pH value of 7.0. Modifications to the protonation state of 71GLU were carried out based on the Bernèche’s method36. To generate the membrane system, the semi-automated processing tool CHARMM-GUI was used with the POPC lipid model. The KcsA protein was embedded in a lipid bilayer consisting of 216 POPC molecules. To enhance the probability of ion transport, the system was placed in a 9 × 9  × 20 nm3 water box with a concentration of K+ and Cl− ions at 0.4 M, consisting of 33,696 water, 218 K+, and 218 Cl−.

MD simulations

All molecular dynamics simulations were performed in the package GROMACS-2019, with the FF14SB and Slipids force fields used for the protein and lipid components, respectively. The water molecules were simulated by the TIP3P model, and the ions by the model of Lee et al.37. Hydrogen bonds were constrained using the linear constraint solver (LINCS) with a time step of 2 fs, and the Verlet scheme was applied to update the neighbor list. Long-range electrostatic interactions were calculated using the particle mesh Ewald (PME) method, with a cutoff of 1.2 nm for electrostatic and van der Waals interactions. The simulation system was maintained at a temperature of 310 K and standard atmospheric pressure, with temperature coupling by the V-rescale thermostat and semi-isotropic Berendsen thermostat for NVT and NPT simulations, respectively.

Firstly, the single bilayer membrane system generated by CHARMM-GUI was minimized for 100 ps, with the protein and lipids allowed to move freely. Then, all heavy atoms except for those in the ion-selective filter (TTVGYG) were restrained with a force constant of 1000 kJ/mol/nm2 and the system was equilibrated for 20 ns. After the single bilayer membrane system reached equilibrium, the system was duplicated along the z-axis to generate a composite bilayer membrane protein system, and all heavy atoms in the protein and lipid components except those of filter were restrained with a force constant of 1000 kJ/mol/nm2 for 20 ns of energy minimization and equilibration. Finally, the simulation protocol of computational electrophysiology in GROMACS (COMPEL) was initiated for 1 µs of production simulation under a fixed charge imbalance Δq = 4 e across the membrane in a fully equilibrated system38. The charge imbalance Δq leaded to an ion concentration gradient ΔC of 14.6 mM and a resultant transmembrane voltage V. The gmx potential tool was used to calculate V with the relative dielectric constant (εr) set as 439,40.

Quantum chemistry calculations

Structures for the calculations were selected from picosecond-scale MD trajectory (Fig. 1b), with one frame per 1 ps for a total of 500 frames. For each frame, the confined K+, the water molecules within 3.5 Å of confined K+ and the residues in the filter region were selected as a cluster model for charge calculations. The broken bond position was saturated with hydrogen. The size of the final structure was 271 to 296 atoms. The ground state was calculated using the Hatree-Fock method and 6–31 g basis set, and Mulliken charge analyses were applied, all of which were carried out in the BDF package41.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.