Introduction

The interplay between the orbital, spin, and structural degrees of freedom is a driving factor of many key properties of solids, including high temperature superconductivity, colossal magneto resistance and metal-insulator transitions. In the last decades, great progress in controlling this interplay to obtain materials with novel functional properties has been made by techniques such as epitaxial strain engineering and the design of heterostructures1,2,3. Adjustments in metal-insulator transition temperatures, modification of magnetic structures, or the creation of superconducting phases show the potential of these methods, which have focused in particular on transition metal oxides such as manganites4 and nickelates5. Driven by the development of new laser sources in recent years, the control over material properties was extended into the time domain by selective excitation of electronic, magnetic, and structural degrees of freedom6,7,8. While significant effort has been spent to coherently control collective excitations such as magnons9,10 and phonons11,12,13,14, there are only few studies on coherent orbital excitations in correlated materials15,16,17. Here, we demonstrate the resonant and coherent excitation of a purely orbital transition at THz frequency in a correlated rare earth quantum material.

The physics of these materials is defined by the rare earth ion’s 4f valence electrons. They are partially shielded from the environment by the filled 5s2 and 5p6 shells, which reduces their interactions and leads to more localized states18. This makes them ideal candidates to study orbital coherence in condensed matter. Enduring interest in the rare earth pyrochlore Tb2Ti2O7 (TTO) (Fig. 1a) stems from its evasion of magnetic order and formation of a strongly correlated magnetic state below temperatures of the scale of the Curie-Weiss constant, 13 K19,20,21,22,23,24, rather than long range magnetic order as originally anticipated25,26. Quantum fluctuations27, structural distortions28 or fluctuations21, hybridization of magnetic and structural fluctuations19, and quadrupolar degrees of freedom29 have all been explored as mechanisms by which magnetic order may be suppressed while preserving the unprotected local moment of the non-Kramers doublet ground state of the Tb3+ 7F6 multiplet in the D3d symmetry crystal field (CF). The first excited crystal field level lies ΔE = hν0 = 1.6 meV (ν0 = 0.4 THz) above the ground state, as schematically shown on the right-hand side of Fig. 1a. Optical measurements show that on cooling TTO into the correlated state, an absorption peak appears at ν0 = 0.45  THz, close to the lowest CF transition energy30. The temperature dependence of its oscillator strength tracks the population difference between the ground and the first excited CF level, which are both doublets31. Since the even symmetry (Eg) of the levels forbids an electric dipole excitation, the absorption is attributed to magnetic dipole coupling32,33. Here, we study the resonant excitation of this CF transition in the time domain. By measuring the magnetic and structural dynamics, we show that not only the population but also the relative phase of the CF levels involved in the wave function of the 4f shell can be controlled.

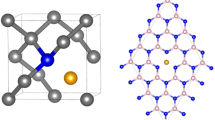
Fig. 1: Cubic pyrochlore structure of Tb2Ti2O7.
figure 1

a Lefthand side: corner-sharing tetrahedra, formed by the Tb ions (other ions are not shown for clarity). Righthand side: Tb3+ 4f CF levels. The orange arrow indicates the transition, which was resonantly excited. b X-ray absorption measured via total fluorescence yield across the Tb L3-edge (gray in the background) and energy dependence of the orbital (028) diffraction peak (black). The inset shows the alternating orientation of the oxygen cages, which distinguish neighboring Tb sites (green). The crystal structures were visualized using the VESTA software41. Source data are provided as a Source Data file.

Full size image

Results and discussion

In order to disentangle the orbital and magnetic dynamics from structural components of this transition, we employed time-resolved resonant and non-resonant x-ray diffraction using 50 fs x-ray pulses at the Bernina beamline of the SwissFEL Free Electron Laser34,35. Methods section “Experimental setup and geometry” and Supplementary Fig. 1 give more details on the experimental setup. For our experiments we use a single crystal of TTO with a (001) surface orientation (sample EP3 from ref. 36). The orbital dynamics were studied by tuning the x-ray photon energy to the Tb L3 edge. Figure 1b shows the photon energy dependence of the structurally forbidden (028) peak together with the x-ray absorption signal collected in total fluorescence yield mode. The intensity of the (028) peak shows a clear enhancement at 7522.5 eV, which originates from a periodic ordering of Tb orbitals caused by rotations of the oxygen cages surrounding them. Ionic motions were detected by following the diffracted intensity changes of the structurally allowed \(\left(\bar{1}37\right)\) diffraction peak.

The single cycle electromagnetic pulses used for the excitation reached peak electric and magnetic fields of 0.75 MV/cm and 0.25 T, respectively, with a central frequency of 0.6 THz as shown in Fig. 2a. The linearly polarized electric and magnetic field components were polarized along the sample [110] and \(\left[1\bar{1}0\right]\) directions, respectively. The same Figure shows the temporal evolution of the change in diffracted intensity of the structural \(\left(\bar{1}37\right)\) and the resonant orbital (028) diffraction peaks following excitation at 5 K sample temperature. We first discuss the time-resolved changes of the \(\left(\bar{1}37\right)\) peak intensity (green, panel b), which is insensitive to induced magnetic or orbital dynamics. Since all optically active phonon modes of TTO have frequencies >2.7 THz30,32, significantly higher than the driving field, they are not resonantly excited. Under these conditions, the ions simply follow the THz pump electric field E(t) in phase, like oscillators driven below their resonance frequency. Due to the large imaginary part of the atomic scattering factors at the Tb L3 edge, these atomic displacements modulate the intensity of the structural diffraction peak linearly. Hence, the associated changes in diffraction intensity are proportional to the electric field E(t), contributing to the change in diffracted intensity according to

$${\left(\frac{\Delta I}{I}\right)}_{{struc}}\left(t\right)={a}_{s}\cdot E\left(t\right),$$
(1)

where as is a constant.

Fig. 2: Time-dependent diffracted peak intensity at 5 K sample temperature and simulation results.
figure 2

a Magnetic field of the THz pump pulses, obtained by electrooptic sampling42. b, c Change in diffracted intensity of the structural \(\left(\bar{1}37\right)\) diffraction peak (green markers) and the resonant (028) diffraction peak (blue markers). Error bars reflect the 1σ (67%) confidence interval. Fourier transforms of the excitation pulse and the oscillatory component of the resonant peak are displayed in the insets. The experimental data are simulated (light solid lines) by fitting the coefficients of Eqs. (1) and (5) to the data. d Simulation results. The resonant excitation induces a coherent superposition between ground state \(|0\rangle\) (blue) and first excited Tb CF level \(|1\rangle\) (red), which reduces their occupation difference ∆n by around 0.1% (e). The off-diagonal term of the density matrix ρ10 (f) encapsulates the coherence of the CF levels, which manifests itself via a macroscopic oscillating magnetic dipole (gray line) due to the collective motion of the Tb spins (black arrows), which oscillate coherently with frequency ν0 = 0.45 THz. Source data are provided as a Source Data file.

Full size image

At early times, the diffraction intensity of the resonant peak (blue, panel c) shows similar behavior, albeit with opposite sign. This behavior is largely expected: the same ionic motion that is measured in the \(\left(\bar{1}37\right)\) peak is likely to also influence the position, orientation and shape of the Tb orbitals due to changes of the CF potential. The time-resolved intensity change of the (028) peak, however, has an important additional feature: a coherently oscillating component that persists beyond the driving pulse. Despite the broad excitation bandwidth, the spectrum of this induced oscillatory component is sharply peaked at ν0 = 0.45 THz, which corresponds to the energy difference ΔE between the resonantly excited levels (see Fourier transforms in panels a and c of Fig. 2).

In order to better understand the origin of this coherent signal, we simulate the dynamics induced by the coherent excitation of the first Tb CF level at ΔE = 1.6 meV. Since further CF levels are separated by ≥10 meV, they can be neglected. For a given ion, the direction of the transient magnetic field selects a preferential basis within the two doublets, coupling one singlet of the ground state doublet \(|0\rangle\) to one partner singlet in the excited state \(|1\rangle\). These pairs of ground and excited states form an ensemble of effective quantum two-level systems (TLS), each described by a wave function \(|\psi \rangle={c}_{0}|0\rangle+{c}_{1}|1\rangle\) (see Supplementary Text 1 for a detailed derivation). Given the moderate exchange and dipolar couplings between different Tb ions of ~ 1 meV estimated from the Curie-Weiss temperature, the short time dynamics of the ensemble is well described by the density matrix formalism for single ions37. The average state of an effective TLS is given by its density matrix ρ:

$$\rho=\left(\begin{array}{cc}\overline{{c}_{0}^{2}} & \overline{{c}_{1}^{*}{c}_{0}}\\ \overline{{c}_{0}^{*}{c}_{1}} & \overline{{c}_{1}^{2}}\end{array}\right),\,{\rho }_{10}={\rho }^{*}_{01}.$$
(2)

The diagonal elements \({\rho }_{00}=\overline{\left|{c}_{0}^{2}\right|}\) and \({\rho }_{11}=\overline{\left|{c}_{1}^{2}\right|}=1-\overline{\left|{c}_{0}^{2}\right|}\) represent the occupation of the ground and the excited state, respectively, while the off-diagonal elements ρ10 and ρ01 capture their phase coherence.

When the atoms are exposed to the magnetic field B(t) of a light pulse, the dynamics of the occupation difference \(\Delta n={\rho }_{00}-{\rho }_{11}\) and the induced coherence ρ10 evolve according to the coupled equations of motion:

$$\frac{d\Delta n\left(t\right)}{{dt}}= i\frac{2d{g}_{J}{{{{\rm{\mu }}}}}_{B}B\left(t\right)}{{{\hslash }}}\left({\rho }_{10}\left(t\right)-{\rho }_{10}^{*}\left(t\right)\right)\\ -\frac{\Delta n\left(t\right)-\Delta {n}_{{eq}}}{\tau };\,\Delta n\left(t=-{\infty }\right)=\Delta {n}_{{eq}}.$$
(3)
$$\frac{d{\rho }_{10}\left(t\right)}{{dt}}=-i{\omega }_{0}{\rho }_{10}\left(t\right)+i\frac{d{g}_{J}{{{{\rm{\mu }}}}}_{B}B\left(t\right)}{{{\hslash }}}\Delta n\left(t\right)-\frac{{\rho }_{10}\left(t\right)}{{\tau }_{c}};\,{\rho }_{10}\left(t=-{\infty }\right)=0.$$
(4)

Here, \({\omega }_{0}=2\pi {\upsilon }_{0}\) is the resonance angular frequency and the matrix element d ≈ 3 can be viewed as the effective magnetic moment of the two-level system. The prefactors \({g}_{J}=3/2\) and μB denote the Landé factor of the Tb 7F6 multiplet and the Bohr magneton. The first term in Eq. (3) describes the coherent build-up of an excited population with instantaneous Rabi frequency \({\Omega }_{R}\left(t\right)=d{g}_{J}{{{{\rm{\mu }}}}}_{B}B\left(t\right)\). The second term describes relaxation back to the equilibrium value \(\Delta {n}_{{eq}},\) with the lifetime of the excited state τ. The first two terms in Eq. (4) describe the unitary evolution of the coherence ρ10, while the last term captures its dephasing over a decoherence time τc with \({\tau }_{c}\le \tau\).

The (028) diffraction peak at the L3-edge probes the electric quadrupoles of the 5d electrons, which sense all 4f quadrupoles through intra-shell Coulomb interaction. As a result our experiment is insensitive to moderate changes in the occupation of only the lowest CF levels. In contrast, the coherence manifests itself as a macroscopic magnetic dipole moment \(\bar{\left\langle \mu \right\rangle }\left(t\right)={tr}\left(\rho \left(t\right){{{\boldsymbol{\mu }}}}\right)=2\mu {{\mathrm{Re}}}\left({\rho }_{10}\right)\left(t\right)\), which can be detected with high sensitivity. Due to the inequivalent quantization axes of the Tb ions defined by their orbital orientations, this transient magnetic ordering of the spins constitutes an additional contribution to the x-ray scattering of the (028) diffraction peak at resonance (see Methods section “Orbital and magnetic contributions to the diffraction intensity of the resonant (028) diffraction peak”). This dynamic magnetic contribution interferes with the static orbital contribution, which strongly enhances its detection sensitivity. Therefore, the total change in diffracted intensity of the (028) peak contains an additional magnetic contribution proportional to \({{\mathrm{Re}}}\left({\rho }_{10}\right)\left(t\right)\) driven by the magnetic field B(t) of the THz pulse. This results in an overall change to the (028) diffraction peak intensity in resonance of

$${\left(\frac{\Delta I}{I}\right)}_{{res}}\left(t\right)={a}_{s,o}\cdot E\left(t\right)+{a}_{m}\cdot {{\mathrm{Re}}}\left({\rho }_{10}\right)\left(t\right),$$
(5)

where as,o and am are constants.

We now use Eqs. (1) and (5) to reproduce the experimental data shown in Fig. 2b, c, respectively. The electric field E(t) of the THz pulse is measured via electro-optic sampling, from which the magnetic field B(t) is calculated. This magnetic field is used to obtain \({\rho }_{10}(t)\) via numerical solution of Eqs. (3) and (4). The parameters \({a}_{s},{a}_{{s\_o}},{a}_{m},{\nu }_{0},{\tau }_{c}\) are adjusted to best fit the data (see Supplementary Table 2 for a summary of the obtained values). Since the induced magnetization is sensitive only to the coherence time τc, the lifetime of the excited state τ cannot be used as fitting parameter and has been fixed instead to 4 ps estimated from the Tb-Tb hopping time given by their interaction energy of 1 meV. The resulting change in diffracted intensity is displayed in Fig. 2b, c as light lines, which agree well with the experimental data. The solution of the differential Eqs. (3, 4) is visualized in panels d-f of Fig. 2.

Following the excitation, the occupation difference (black curve) decreases, as ~0.1% of the Tb ions are excited from the ground state to the higher energy level. The coherent superposition of the two CF levels is reflected in coherent oscillations of the off-diagonal term ρ10 of the density matrix (Fig. 2f). These oscillations with frequency ν \({\nu }_{0}=0.45 \,{\rm {THz}}\) persist on the order of the coherence time τc beyond the end of the exciting pulse. The obtained coherence time τc of 2.4 ± 0.4 ps is of the same order as the 4 ps timescale set by Tb-Tb exchange and dipolar couplings, which sets an upper limit for the intrinsic lifetime of the excited state. Inelastic scattering from, or hybridization with acoustic phonons can further reduce the lifetime, indicating that the decoherence is dominated by the decay of the excited state19,21,32,38.

Finally, we discuss the temperature dependence of the oscillations, i.e., the coherence of the ensemble. Figure 3a–c show the amplitude, frequency and coherence time of the oscillatory magnetic component extracted from fits of the model (Eqs. (1) and (5)) to the data. In agreement with the model, the amplitude of the induced coherence follows Boltzmann statistics \(\Delta {n}_{{eq}}(T)=\tanh \left(\Delta E/2{k}_{B}T\right)\), reflecting its linear dependence on the occupation difference \(\Delta {n}_{{eq}}\) between the two CF states before excitation (see Eq. 3 and Supplementary Eq. 22). The observed frequency shows a slight increase from 0.39 to 0.45 THz as the temperature is lowered to 5 K. This shift presumably arises due to the onset of local correlations (with acoustic phonons or among Tb) that couple to the Tb ions, shifting and quasi-statically splitting the crystal field spectrum21,39. Signatures of induced coherence are found up to 50 K with a constant coherence time of 2.4 ps, suggesting that temperature independent relaxation of excitations (e.g., their hopping to a neighbor ion) dominates the dephasing. Reducing the magnetic exchange paths by diluting the rare earth ion with non-magnetic Y could enhance coherence times and shed more light on the magnitude of coupling between Tb and the lattice, which is unaffected by dilution and likely the dominant remaining decay channel17. In summary, our results demonstrate the persistence of quantum coherence even in the extreme limit of dense rare-earth compounds and higher frequencies up to 50 K, establishing a link with the observation of coherence in more dilute samples, which led to the proposal of using rare earth ion 4f shells for quantum computing processing40.

Fig. 3: Temperature dependence of the induced magnetic dipole.
figure 3

The data points show the amplitude (a), frequency ω0 (b) and coherence time τc (c) of the oscillatory magnetic component observed in the diffraction intensity change of the resonant peak. They have been extracted from fits of the model coefficients (Eqs. (1) and (5)) to the data. Error bars reflect the 1σ (67%) confidence interval. The dashed black line visualizes the occupation difference \(\Delta {n}_{{eq}}(T)\) of the two levels calculated from Boltzmann statistics (right side vertical axis). See Supplementary Fig. 2 for the individual time-traces of the orbital and structural peak. Source data are provided as a Source Data file.

Full size image

More generally the coherent control of orbitals constitutes a new tool for the ultrafast control of materials to manipulate magnetic properties on fs-ps timescales with elemental selectivity. The microscopic pattern of the oscillatory magnetic response depends on the polarization and the propagation direction of the THz pulse, since a different orientation of its magnetic field will select a different pair of effective two-level systems from the driven 4-level system. The excitation with linearly polarized light—as used here—induces an oscillatory magnetization on atomic sites selected by the crystal field transition. If circularly polarized light is used, the THz excitation will couple a pair of magnetized states in the ground and excited CF doublet that each carry a static magnetic moment. Such driving thus transfers angular momentum into the Tb ions 4f shell, inducing quasi-static magnetization, which rises during the pulse and persists on the order of the life time τ beyond the pulse (see Supplementary Text section 1.9). This ultrafast magnetic pulse reaches moments of the order of a Bohr magneton per site, creating internal fields of around 20 mT in Tb2Ti2O7. So far most efforts to achieve ultrafast control of materials has centered on the concepts of photodoping or the excitation of collective excitations such as phonons, magnons or electromagnons. We envision the coherent control of orbitals demonstrated here to become part of this toolbox to explore out of equilibrium phases of materials and to tune collective properties in analogy to the equilibrium control of orbital polarization and occupation by strain, fields and pressure. Further developments of this technique might open new ways to probe correlations and entanglement among ions in close proximity.

Methods

Supplementary Information is available for this paper.

Experimental setup and geometry

The experimental geometry is shown in Supplementary Fig. 1. The THz pulses (yellow) were generated outside the chamber by optical rectification of 7.4 mJ, 100 fs, 800 nm pulses in LiNbO3. They were guided through an 8 mm thick ZEONEX window into the vacuum chamber and focused by a 2inch diameter, 2inch focal distance parabolic mirror onto the sample. Their field strength and spectral content was characterized in vacuum by electrooptic sampling with 100 fs 800 nm pulses (red) in a 100um thick GaP crystal mounted next to the sample. The FWHM diameter of the 800 nm sampling pulses on the GaP was 90um, slightly larger than the 75um diameter x-ray pulses (dark blue), which were both guided through a hole in the parabolic mirror onto the sample, collinearly with the THz pulses. The photon energy of the 50 fs x-ray pulses was defined with a double crystal Si (111) monochromator to 7522.5 eV with a bandwidth of 1 eV. In diffraction condition of the (028) and \(\left(\bar{1}37\right)\) peaks, the incidence angle of the p-polarized THz pulses was 58.7° with respect to the sample surface. Due to the large refractive index of n > 7.3 within the spectral content of the THz pulses (extracted from ref. 36), they were strongly refracted into the sample, almost propagating along the [001] sample surface normal direction with an angle of 86° to the sample surface. At the angles given above, the penetration depth of the x-ray pulses along the surface normal is 4.6 µm, limited by the absorption of the material. The probed region is thus well within the region excited by the THz pulse, whose absorption length normal to the sample is around 40 µm at the peak of the absorption at 5 K (taking the intensity as a measure). The electric and magnetic field components were polarized along the [110] and \(\left[1\bar{1}0\right]\) directions. The sample was cooled with a helium flow cryostat to a base temperature of 5 K.

Orbital and magnetic contributions to the diffraction intensity of the resonant (028) diffraction peak

Static orbital contribution

The site symmetry of the Tb ion at Wyckoff position 16c of the space group Fd-3m (227) is −3m with a multiplicity of 16. The symmetry operations generate 4 unique Tb ions at positions Tb1 @ (0, 0, 0)cubic, Tb2 @ (3/4, 1/4, 1/2)cubic, Tb3 @ (1/4, 1/2, 3/4)cubic, and Tb4 @ (1/2, 3/4, 1/4)cubic. The remaining Tb ions in the unit cell are generated by translations of the unique Tb atoms by (0, 0, 0), (0, 1/2, 1/2), (1/2, 0, 1/2), and (1/2, 1/2, 0). Because of the local −3m symmetry, the only quadrupole moment that can contribute to the (028) equilibrium intensity is \({Q}_{3{z}^{2}-{r}^{2}}=\frac{1}{2}\left(2{f}_{{zz}}-{f}_{{xx}}-{f}_{{yy}}\right)\), where z points along the local C3 symmetry axis.

Dynamic magnetic contribution

In the following, we evaluate the contribution of magnetic scattering to the (028) diffraction intensity due to transient magnetic moments \(\vec{{{{{\rm{m}}}}}_{i}}\) induced by the resonant excitation of the first CFL on the 4 unique Tb sites denoted by the index i. Following equation (35), the induced magnetic moment can be evaluated by projecting the [1-10] polarized B-field onto the local quantization axis xyzlocal,i. Using the local Cartesian coordinate with z parallel to the C3 symmetry axis for Tb1 @ (0, 0, 0)cubic, we obtain x // [1-10], y // [11-2], and z // [111]. Supplementary Table 1 summarizes the positions, quantization axis as well as the induced magnetic moments of all 4 unique Tb ions. The magnetic form factor \({\vec{{{{\rm{F}}}}}}_{m}(t)={\sum}_{i}\vec{{{{{\rm{m}}}}}_{i}}{({{{\rm{t}}}}){{{\rm{e}}}}}^{2\pi i\left({hx}+{ky}+{lz}\right)}\) among the four Tb atoms can then be evaluated as:

$${\vec{{{{\rm{F}}}}}}_{m}(t)\approx -3.4M(t)\cdot \left(1,-1,0\right),$$

with \(M(t)={({g}_{J}{\mu }_{B})}^{2}\sin ({{{{\rm{\omega }}}}}_{0}t){\int }_{-\infty }^{t}d{t}^{{\prime} }{B}_{0}({t}^{{\prime} }){e}^{-(t-{t}^{{\prime} })/{\tau }_{c}}\) following from equation (32). The total magnetic scattering factor of a single unit cell is just a multiplication of the above form factor by the factor of four. The incident x-ray pulses were horizontally polarized along εi = [1-10] and the (028) peak was measured without polarization analysis. Since magnetic scattering is given by the projections of \({\vec{{{{\rm{F}}}}}}_{m}//\left(1,-{{\mathrm{1,0}}}\right)\) onto the propagations of the incident and scattered x-rays as well as its cross product, there is a finite contribution of magnetic scattering to the (028) reflection, which can interfere with the orbital scattering given by \({Q}_{3{z}^{2}-{r}^{2}}\) and induces a linear modulation of the orbital peak intensity.