Introduction

A solid grasp of thermal phonon dynamics in phase change materials is critical to better understanding the phase transition mechanism and engineering materials for thermal energy conversion and storage. Over the past decade, detailed first-principles phonon calculations based on density functional theory (DFT) at 0 K and three-phonon scattering1,2 have become routine. These traditional methods, however, have been proven difficult near phase transitions and at high temperatures due to the structural instabilities at 0 K and increased higher-order anharmonic interactions. Despite further developments of four-phonon scattering3, temperature-dependent effective potential (TDEP)4,5, self-consistent phonon theory6, the stochastic self-consistent harmonic approximation (SSCHA)7,8, and unified theory9, phase change materials remain largely unexplored because of the computational constraints in efficiently combining temperature effects with higher-order phonon scattering. This significantly impedes our understanding of phonon dynamics and thermal conductivity in phase change materials.

Germanium telluride (GeTe) provides an excellent yet challenging platform to study thermal transport behavior near temperature-induced phase transitions. The proximity to dynamic instability and the unique bonding characteristics of IV–VI materials further complicate the thermal transport picture. GeTe undergoes a structural phase transition from the rhombohedral to the cubic crystal structure near 650 K depending on the carrier concentration10,11,12,13, setting it apart from other IV–VI materials, and is attractive for phase change applications such as phase change memory cells14. In addition, GeTe is a prime candidate for thermoelectric applications and is considered a potential replacement for toxic lead telluride (PbTe)-based materials, with a high ZT value of up to \(2.5\) at around 700 K15. GeTe has also shown potential for spintronic devices due to its strong spin-orbit coupling and Rashba effect16. The lattice thermal conductivity of GeTe plays a crucial role in the aforementioned applications. Therefore, a sophisticated, atomic-scale picture of lattice thermal conductivity of cubic GeTe will not only advance our fundamental understanding of lattice dynamics near crystalline-to-crystalline phase-changes in general but also serve as the solid foundation for optimizing its performance in real applications.

Interestingly, experimental data from multiple independent groups all show an unexpectedly increasing trend for the lattice thermal conductivity of high-temperature phase cubic GeTe17,18,19,20,21,22. This challenges the conventional wisdom that at high temperatures, the lattice thermal conductivity of crystalline materials typically decreases with temperature, attributed to enhanced phonon-phonon scattering. Theoretical and computational studies are, however, scarce, leaving this abnormal trend yet to be explained. Fortunately, ML algorithms in the form of advanced linear regression have been recently applied to thermal transport modeling in crystals, which can account for finite temperature effects while extracting higher-order interatomic force constants (IFCs) with much greater efficiency23. However, applications of these algorithms to phase change materials are still in their infancy. To the best of our knowledge, only one study included the quartic IFCs for cubic GeTe at one temperature (800 K)24. The scarcity of computational data and the lack of temperature-dependent computational studies compel us to conduct this study to uncover the mystery of the experimental trend.

Herein, we carry out a thorough study of thermal transport in cubic GeTe, combining machine learning (ML)-assisted first-principles calculations and inelastic X-ray measurements (Fig. 1a). The computational approach in this study integrates considerations of temperature dependence, four-phonon scattering, and the coherence contribution, which is among the highest levels of theory so far25,26,27,28. More specifically, we use Bayesian Ridge (BR) regression to train linear models of thermalized force-displacement data generated from first-principles calculations at 693 K and higher. We efficiently extract the IFCs up to the fourth order, allowing us to consider the effects of temperature-dependent IFCs and four-phonon scattering. Additionally, by extending the unified theory9 to embrace the real-space displacement approach, we provide a first look into coherence effects in a high-temperature phase and with four-phonon scattering included. We corroborate the computational phonon dispersion and lifetimes with the first inelastic X-ray scattering (IXS) measurements of cubic GeTe at 693 K. This work provides a general computational framework to study a wide range of phase change materials.

Fig. 1: Overview of Methodology.
figure 1

The schematic of this work is where we (a) carried out integrated computational and experimental work to better understand the thermal transport properties of cubic GeTe. Using machine-learned IFCs and developing the real-space displacement approach for the unified theory, we were able to include effects from high temperatures, four-phonon scattering, and coherence (b) converted from a plane wave basis to a localized basis composed of pseudo-atomic orbitals (PAOs) to investigate pairwise bonding in cubic GeTe.

Full size image

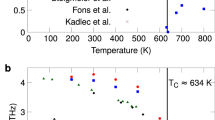
Remarkably, our lattice thermal conductivity calculations reproduce the increasing trend in temperature-dependent thermal conductivity that was universally observed across different experiments. This abnormal, strongly increasing trend awaits demystification, which motivated us to perform temperature-dependent interatomic bonding calculations (Fig. 1b). We correlate this unusual thermal conductivity trend in cubic phase GeTe to its peculiar interatomic bonding behavior, which are known to be unique for IV–VI materials generally. Specifically, we posit that this temperature-dependent bond strengthening between second-nearest neighbors, namely Ge-Ge and Te-Te bonds along the <110> direction, substantially contributes to the increasing thermal conductivity. This study not only offers the first insights into the unusual temperature dependence of thermal conductivity in cubic GeTe but also offers a new perspective of thermal transport near phase transitions in general.

Results and discussions

At 693 K, the X-ray diffraction (XRD) pattern of our GeTe sample shows that it has completed the phase transition from the rhombohedral to the cubic phase (Fig. 2a). More details can be found in SI. The calculated phonon dispersion at 693 K using renormalized harmonic IFCs fitted via BR regression is shown in Fig. 2b, where the higher order terms were renormalized onto the harmonic IFCs to prevent the imaginary frequencies indicative of an unstable structure. A cutoff of 10.5 Å was applied to include the long-range interactions. Our experimental phonon dispersion from IXS is also plotted in Fig. 2b. The calculated phonon frequencies agree well with those measured by IXS. The phonon dispersion of cubic GeTe is similar to that of IV–VI family, such as PbTe29, SnTe30, and SnSe31, which share the same space group of Fm3m. The phonon lifetimes of the acoustic and optical phonon modes of cubic GeTe at 693 K, extracted by IXS and calculated using both third- and fourth-order IFCs, are shown in Fig. 2c. The lifetimes exhibit an ω−2 dependence in the low-frequency range. Notably, including four-phonon processes significantly improves agreement with the experimental data, especially for the frequency range between 1 and 3.5 THz, the primary heat carriers, as shown in Fig. 2d. This suggests that including four-phonon scattering is essential. The comparison between calculations and experiment validates the accuracy of our ML-trained models from first-principles calculations.

Fig. 2: Structures before and after phase-change and thermal transport properties of GeTe from calculations and experiments.
figure 2

a GeTe undergoes a phase transition from the rhombohedral to cubic crystal structure around 650 K. b Calculated and measured phonon dispersion of GeTe single crystal at 693 K show good agreement. c Calculated and measured phonon lifetimes of GeTe at 693 K. The results follow a rough 1/ω2 trend, shown by the dark blue dashed line. The shaded region highlights the overestimation of lifetimes if only three-phonon is considered. d Spectral thermal conductivity contribution at 693 K indicates that the main contributors are between 1 and 3.5 THz.

Full size image

We then calculated the lattice thermal conductivity as a function of temperature by using the IFCs as input to solve the phonon Boltzmann transport equation (BTE). A comparison between our calculated lattice thermal conductivities32 and experimental data from the literature17,18,19,20,21,22 and those from others’ TDEP calculations33 are shown in Fig. 3a, b, respectively. Although TDEP with three-phonon scattering was able to match well with the experimental data of the rhombohedral phase, it drastically overestimated the thermal conductivity in the cubic phase. Our calculations with only three phonon scattering are in the same ballpark as TDEP. A more detailed comparison can be found in SI. However, by including four-phonon scattering, the thermal conductivity dropped by roughly half and fell into the experimental window33, and the good agreement holds for all other temperatures we calculated. This is further evidence that four-phonon scattering is vital for modeling thermal transport in cubic GeTe.

Fig. 3: Calculated thermal conductivity compared to experiments in literature.
figure 3

a Lattice thermal conductivity of GeTe at various temperatures according to experiment (hollow triangular markers and yellow shaded region)17,18,19,20,21,22 and our calculations. The gray area indicates the transition temperature range of GeTe33. Temperature-dependent lattice thermal conductivity measurements of PbTe34 and PbSe32 from the literature are also shown for comparison. b Lattice thermal conductivity of GeTe previously calculated via TDEP with three-phonon scattering33 (hollow rectangular markers) along with our calculations using BR-trained third-order IFCs (pink-filled circular markers), our calculations using BR-trained third- and fourth-order IFCs (magenta circular markers), and the latter with added corrections from coherence (dark red circular markers). The inset shows the contribution to thermal conductivity by coherence with both three- and four-phonon scattering included.

Full size image

We also accounted for the effect of coherence by modifying the unified theory to adopt the finite difference approach and to include four-phonon scattering rates. The coherence contribution is minor compared to the particle-like transport, similar to prior calculations on Tl3VSe425. Specifically, the coherence only increases total thermal conductivity by 1–2% (Fig. 3 inset), although including fourth-order phonon scattering leads to an increased broadening of phonon linewidth. This is because the coherence thermal conductivity, κC, shows a Breit-Wigner behavior. If the phonon linewidth is close to the Breit-Wigner resonance value (determined by the separation between phonon branches), phonon states can be viewed as “driven” by the scattering, meaning that the quantum coherence between the phonon states can be preserved. Otherwise, κC is small, which is the case for GeTe.

The most remarkable finding of this work is the increasing trend in the calculated lattice thermal conductivities beginning at 750 K and continuing through 850 K. This is the first computational study to reproduce the experimentally observed anomaly of lattice thermal conductivity vs. temperature. We carefully rule out a few possible explanations for the increasing trend. First, we are aware that the bipolar effect can produce an increasing trend in thermal conductivities at high temperatures. However, the increase in GeTe appears to be much steeper compared to PbSe and PbTe32,34,35 (Fig. 3). Moreover, the presence of Ge vacancies should make the sample p-type and thus render bipolar effects negligible. Second, since we only considered the lattice thermal conductivity from both our calculation and experiments, the electronic contribution, by definition, has already been subtracted from the total thermal conductivity and is not relevant to this discussion.

We can leverage the detailed calculations to gain insight into the underlying mechanisms for the unusual lattice thermal conductivity increase. Taking a closer look at the temperature dependence of the phonon dispersion shown in Fig. 4a, the most profound change in the frequency occurs in the transverse optical (TO) modes at the Gamma point. The TO mode frequency at the zone center vs. temperature closely aligns with the thermal conductivity trend (Fig. 4b). Over the past few years, in search of higher-performing thermoelectric materials, studies of phonon dynamics in IV–VI materials have attributed ultralow thermal conductivity to the soft TO modes induced by ferroelectric instability, and the proximity to the ferroelectric instability is typically adjusted via strain and/or alloying36,37,38. While TO mode softening in IV–VI materials is often related to the Peierls distortion, the Peierls distortion disappears in the cubic phase. As the temperature goes above the ferroelectric transition, the hardening of the TO mode over the temperature range we investigated is consistent with the literature39 and could be related to the increasing stability of the cubic phase. The increasing thermal conductivity is further supported by the temperature dependence of the Gruneisen parameter (Fig. 4c), which shows a roughly inverse relationship to thermal conductivity as illustrated in Fig. 4d. From 725 K to 850 K, both the increase in the TO mode frequencies and the decrease in the Gruneisen parameter indicate reduced anharmonicity, in contrast to the usual behavior with rising temperature.

Fig. 4: Calculated temperature-dependence of thermal properties.
figure 4

Calculated temperature-dependence of (a) phonon dispersion, (b) TO mode frequency at zone center, (c) spectral Gruneisen parameters, (d) total Gruneisen parameter.

Full size image

The decreasing anharmonicity and hardening of the TO mode with temperature are curious. Given that the bonding characteristics of IV–VI chalcogenides are unique, exhibiting properties of both metallic and covalent bonds, or ‘metavalent’ bonding40,41, we were motivated to dive deeper into the temperature-dependent bonding behaviors of cubic GeTe. To our knowledge, the understanding of the bonding and its temperature dependence in cubic GeTe is quite limited based on the current literature. There is a recent study of pairwise correlated atomic motion in GeTe42, but one cannot confidently deduce bonding strengths or thermal conductivity from it.

To go one step deeper than previous studies, we calculated Crystal Orbital Hamilton Population (COHP) curves at 693 K, 775 K, and 850 K to probe the temperature dependence of interatomic bonding in cubic GeTe. It should be emphasized that the COHP calculations are in no way dependent on the force constant calculations, thus providing an independent way to probe atomic pair interactions. Each COHP curve corresponds to one thermalized configuration of the supercell and represents an average of all bonds within the specified cutoff radii and that consist of the specified pair of elements. In these plots, negative values indicate bonding electrons, while positive values indicate anti-bonding electrons. It is difficult to notice any temperature dependent bonding from examining only the COHP vs. energy curves. Rather, to gauge the strength of bonding/anti-bonding interactions, one can integrate the COHP curves with respect to energy, where the value of the integrated COHP (iCOHP) at the Fermi level can be interpreted as an overall bonding/anti-bonding strength.

Examining the iCOHP results, the strongest bonds are between nearest neighbor Ge and Te pairs in the <100> directions, where p-orbital overlap is extensive, as expected. However, these bonds do not show a temperature dependence, and we observe a negligible 0.4% change in bonding strength with temperature from 693 K to 850 K. The covalent interactions of the second-nearest neighbor Ge-Ge and Te-Te bonds are much weaker. However, quite remarkably, the Ge-Ge and Te-Te bonds appear to increase in strength by 8.3% and 103%, respectively. The larger percentage increase of Te-Te bonds can be attributed to the fact that they are weaker since the magnitudes of the COHP increase in both the Ge-Ge and Te-Te bonds are similar. The increasing bonding strengths of Ge-Ge and Te-Te with temperature are peculiar, aligning with the reduced anharmonicity discussed earlier. We posit that while Ge-Te bonds are consolidated closer to the phase transition to stabilize the cubic structure, the second-nearest neighbors of Ge-Ge and Te-Te are not as settled, only reaching peak strength with further temperature increases. It should also be noted that in experimental cubic GeTe samples where Ge vacancies are thought to be common, the Fermi level lies closer to the valance band43. Since the difference in the iCOHP curves between 850 K and 693 K (dashed turquoise lines in Fig. 5) stays roughly constant right below the Fermi level as shown in Fig. 5, we do not expect electronic effects from p-doping to alter this bonding picture. Therefore, we believe that this unexpected bond strengthening is a strong contributor to the observed increasing trend.

Fig. 5: Calculations of temperature-dependent bond strengths.
figure 5

Comparison of COHP and integrated COHP (iCOHP) bonding curves at 693 K and 850 K for closest (a) Ge-Ge bonds (3.6–5.0 Å), and (b) Te-Te bonds (3.6–5.0 Å), and (c) Ge-Te bonds (0.1–3.5 Å). Values less than zero indicate bonding states, while values greater than zero indicate anti-bonding states. The left subplots show the COHP curves and the difference (labeled as ∆iCOHP850K, 693K) between the iCOHP curves for 850 K and 693 K, while the right subplots are the iCOHP curves with respect to energy with a narrow view near the Fermi level. The left subplots also show. The iCOHP curves show a decisive increase in bonding strengths for the Ge-Ge and Te-Te bonds, while hardly any difference exists for the Ge-Te bonds.

Full size image

Finally, we note that this increasing thermal conductivity at temperatures above that of the phase transition temperature is not just observed in GeTe. SnTe, which also undergoes a rhombohedral-to-rocksalt phase transition at much lower temperatures, exhibits increasing thermal conductivity versus temperature44. We note that the authors of the study of SnTe attributed this increasing thermal conductivity to the electronic contribution but that they also expressed doubts over the accuracy of the Lorenz number in their case. Thus, SnTe might behave similarly to GeTe at temperatures near its phase transition if the electronic contribution to thermal conductivity is properly calculated. Even more fascinating, we also find similar properties of phase transitions for SnSe, namely TO mode softening near the phase transition temperature of ~750–800 K45 and increasing lattice thermal conductivity (along certain crystal axes) just above the phase transition temperature46. Given that SnSe transitions from the Pnma to the Cnma crystal structures, differing from GeTe and SnTe, this suggests that the findings herein could have broad implications beyond GeTe, providing a pathway to understanding thermal transport near phase transitions more generally.

In summary, we applied a comprehensive approach combining emerging computational methods and experimental IXS measurements to study thermal transport in the high-temperature cubic phase of GeTe. Our calculations of the lattice thermal conductivity show an abnormally increasing trend starting from ~750 K, which aligns with the experimentally observed trend. We attribute the cause of this abnormal trend to a bond strengthening of second-nearest neighbor Ge-Ge and Te-Te bonds. We also highlight that the calculated phonon lifetimes and thermal conductivity with four-phonon scattering included are in much better agreement with IXS experimental data than calculations that only account for three-phonon processes. The use of a modified version of the unified theory and leveraging BR regression to efficiently train high-order linear models from first-principles data allowed us to properly account for the temperature dependence of thermal transport properties while considering four-phonon scattering and coherence effects simultaneously, which has been previously prohibitive. This work reconciles the significant discrepancies between calculated and experimentally measured thermal conductivity in the literature and provides new insights into the unusually increasing lattice thermal conductivity trend of cubic GeTe. More broadly, this work demonstrates an efficient and thorough pathway toward accurate modeling of highly anharmonic materials near phase transitions and/or at high temperatures that have promise for phase change, thermoelectric, and other energy applications.

Methods

Experiments

We purchased GeTe crystals from 2D Semiconductors. The samples were grown using the state-of-art flux zone technique. Before the IXS measurements, we performed XRD at room temperature to screen the samples. Details can be found in SI. We carefully selected a single crystal with a size of \(107\,\mu m\times 485\,\mu m\times 550\,\mu m\) for IXS measurements. To ensure a complete phase transition from the rhombohedral to the cubic phase, we heated the GeTe crystal to 693 K. The XRD reflection pattern of GeTe at 693 K confirmed the cubic phase and indicated good single crystallinity. The IXS measurements were conducted using beamline 30-ID at the Advanced Photon Source (APS), Argonne National Laboratory. IXS is a photon-in, photon-out spectroscopy technique used to probe the dynamics of phonons. This method involves directing a highly focused X-ray beam at a sample and analyzing the energy and momentum transfer that occurs when the X-rays scatter inelastically off the phonons. The high-energy-resolution inelastic X-ray spectrometer (HERIX) at APS 30-ID is a state-of-the-art spectrometer that provides high resolving power, micro-focused beam, nine analyzers, and large momentum transfer47 and we have performed IXS using it on semiconductors29,48 and hybrid materials49,50,51. The instrument operates at 23.7 keV, and the instrument energy resolution was determined prior to measurement to be 1.5 meV. Measured energy spectra were fitted with Lorentzian peaks convoluted with a pseudo-Voigt function to simulate instrument resolution. We performed three to five repeated energy scans and averaged the data for every q point to reduce statistical noise. After fitting the elastic and phonon peaks at each q point, we obtained the mode-dependent phonon frequencies and line widths. The inverse of phonon line width gives the phonon lifetime. An example of the raw data and the fitting curve is shown in Fig. 6.

Fig. 6: Illustration of IXS Data Fitting.
figure 6

Energy spectra from IXS measurement (blue circles) of the TA mode at q = 0.6 along [100] for cubic GeTe single crystal at 693 K characterized by an elastic peak centered at zero energy and inelastic peaks associated with the creation and annihilation of phonons. Cyan and red curves represent the instrumental resolution function and fitting core based on the Lorentzian function, respectively. The solid blue curve denotes the convolution between the resolution function and the fitting core.

Full size image

Computation

Four-phonon scattering of high-temperature phase

To efficiently extract effective higher-order IFCs at finite temperatures, we adopted the BR regression algorithm to train linear models of force-displacement data generated from DFT calculations, with each set of force-displacement data corresponding to a specific temperature. The efficiency of this process stems from the ability to construct linear models based on sparse solutions for underdetermined systems. We trained the linear models using the hiPhive package23, which interfaces with the scikit-learn ML library and its BR regression algorithm implementation. All reference data was split such that 80% was used for training and 20% was saved to validate the model. More specific details about BR regression and its advantages, as well as the training of the IFCs, can be found in SI. All of the force-displacement data were from configurations based on a 5 × 5 × 5 cubic GeTe supercell consisting of 250 atoms. More details regarding the DFT calculations can be found in SI. The optimized lattice constant using DFT calculations corresponding to 0 K was found to be 6.02 Å, which is within the experimental range of 6.016–6.022 Å for temperatures between 693 K and 800 K52.

To generate the temperature-specific sets of displacements, we used a self-consistent phonon method, also implemented in the hiPhive package. In this iterative process, harmonic force constants were calculated and used to generate new configurations by randomly populating the normal modes with a distribution corresponding to the desired temperature53. This idea is similar to that employed in SSCHA8, but with the equilibrium positions frozen. More details about the self-consistent phonon method, including a flowchart, can be found in the SI.

Once these temperature-specific sets of displacements were generated, we performed DFT calculations for each configuration to accurately obtain the corresponding forces. We used the resulting force-displacement data to obtain second, third, and fourth-order effective IFCs for each temperature using linear models trained with BR regression. In this way, thermal averaging effects are baked into the trained linear models and, thus, the predicted force constants. We used cutoffs of 10.5 Å, 8.0 Å, and 5.0 Å for the second, third, and fourth-order IFCs, respectively, to construct the linear models. We are aware of the long-range interactions typical of IV–VI rock salt structures,54 and a more detailed discussion on long-range interactions is included in SI. To best account for these long-range interactions, we used the cutoff of 10.5 Å, which is the maximum allowed for our 250-atom supercell, to train the second-order model. More discussions on long-range interactions can be found in SI. For our calculated phonon dispersion, we used calculated Born effective charges and dielectric constants from DFPT to apply non-analytical term corrections (see SI for more details on the DFPT calculations). Further increasing the third-order cutoff made little difference regarding the calculated thermal conductivity. Our fourth-order cutoff of 5.0 Å includes second-nearest neighbors, typically sufficient to converge fourth-order effects55. Notably, the fitting of the fourth-order IFCs, typically prohibitive, only took a few minutes using BR regression.

Using the IFCs as input, we solved the BTE iteratively for three-phonon processes and used the relaxation time approximation (RTA) for four-phonon processes. It is prohibitively expensive to solve the BTE iteratively for four-phonon processes. Fortunately, the Umklapp processes contribute significantly more to the overall scattering rates in cubic GeTe (see Fig. S2 in Supplementary information), justifying the treatment of four-phonon calculations using the RTA55. More details regarding the BTE calculations can be found in SI.

Coherence contribution

We applied a correction to the thermal conductivity by including the quantum coherence effect. This was motivated by the unified theory9, which shows that broadening the phonon branches can lead to quantum coherence and contribute to lattice thermal conductivity. The original unified theory was only shown to be compatible with the DFPT framework, and only included the coherence contribution from the third-order IFCs. We extended it to incorporate IFCs generated by the real-space displacement approach and include the coherence thermal conductivity from both the third and fourth-order IFCs (Fig. 7). This new implementation allows for (1) applying the unified theory to more complex materials in general because of the use of input from the real-space displacement approach instead of DFPT in reciprocal space; (2) including the four-phonon scattering contribution in the coherence term because the BR regression method drastically accelerated the fitting process and made the fourth-order IFCs accessible. We confirm the consistency of our approach with the original unified theory by calculating the thermal conductivity of \({CsPbB}{r}_{3}\), as shown in the Supplementary information.

Fig. 7: Comparison between the original unified theory recipe and our modification.
figure 7

Incorporating real-space displacement method enables computation for more complicated structures with larger unit cells.

Full size image

The coherence contribution to lattice thermal conductivity is denoted by

$${\kappa }_{C}^{\alpha \beta }= \frac{{\hslash }^{2}}{{k}_{{{\rm{B}}}}{T}^{2}}\frac{1}{{{\mathcal{V}}}{N}_{{{\rm{c}}}}}{\sum}_{{{\bf{q}}}}{\sum}_{s\ne {s}^{{\prime} }}\frac{\omega ({{\bf{q}}})_{s}+\omega ({{\bf{q}}})_{{s}^{{\prime} }}}{2}{V}^{\alpha }({{\bf{q}}})_{s,{s}^{{\prime} }}{V}^{\beta }({{\bf{q}}})_{{s}^{{\prime} },s}\\ \times \frac{\omega ({{\bf{q}}})_{s}\bar{N}({{\bf{q}}})_{s}\left(\bar{N}({{\bf{q}}})_{s}+1\right)+\omega ({{\bf{q}}})_{{s}^{{\prime} }}\bar{N}({{\bf{q}}})_{{s}^{{\prime} }}\left(\bar{N}({{\bf{q}}})_{{s}^{{\prime} }}+1\right)}{4{\left(\omega ({{\bf{q}}})_{s}-\omega ({{\bf{q}}})_{{s}^{{\prime} }}\right)}^{2}+{\left(\Gamma ({{\bf{q}}})_{s}+\Gamma ({{\bf{q}}})_{{s}^{{\prime} }}\right)}^{2}}\\ \times \left(\Gamma ({{\bf{q}}})_{s}+\Gamma ({{\bf{q}}})_{{s}^{{\prime} }}\right)$$
(1)

where \(\omega ({{\bf{q}}})_{s}\) and \(\Gamma ({{\bf{q}}})_{s}\) are the phonon frequency and linewidth, respectively, with the latter calculated using both the third and fourth order IFC, and \(\bar{N}({{\bf{q}}})_{s}={\left(\exp \left(\hslash \omega ({{\bf{q}}})_{s}/\left({k}_{{{\rm{B}}}}T\right)\right)-1\right)}^{-1}\) is the Bose-Einstein distribution. The generalized group velocity matrix is given by

$${V}^{\beta }({{\bf{q}}})_{s,{s}^{{\prime} }}={{{\mathcal{E}}}}^{*}({{\bf{q}}})_{s,b\alpha }{\nabla }_{{{\bf{q}}}}^{\beta }{\sqrt{D\left({{\bf{q}}}\right)}}_{b\alpha,{b}^{{\prime} }{\alpha }^{{\prime} }}{{\mathcal{E}}}({{\bf{q}}})_{{s}^{{\prime} },{b}^{{\prime} }{\alpha }^{{\prime} }}$$
(2)

where the unitary transformation \({{{\mathcal{E}}}}^{\star }({{\bf{q}}})_{s,b\alpha }D({{\bf{q}}})_{b\alpha,{b}^{{\prime} }{\alpha }^{{\prime} }}{{\mathcal{E}}}({{\bf{q}}})_{{s}^{{\prime} },{b}^{{\prime} }{\alpha }^{{\prime} }}={\omega }^{2}({{\bf{q}}})_{s}{\delta }_{s,{s}^{{\prime} }}\) diagonalizes the dynamical matrix \(D({{\bf{q}}})\). Conventional phonon packages based on the real-space displacement approach, such as Phonopy, can provide the dynamical matrix \(D({{\bf{q}}})\) and its gradient \({\nabla }_{{{\bf{q}}}}D\left({{\bf{q}}}\right),\, {{\rm{but}}}\) do not directly support the calculation of \({\nabla }_{{{\bf{q}}}}\sqrt{D\left({{\bf{q}}}\right)}\). Our solution is to obtain the matrix elements of \({\nabla }_{{{\bf{q}}}}\sqrt{D\left({{\bf{q}}}\right)}\) by numerically solving the matrix equation

$${\sqrt{D\left({{\bf{q}}}\right)}\nabla }_{{{\bf{q}}}}\sqrt{D\left({{\bf{q}}}\right)}+\left({\nabla }_{{{\bf{q}}}}\sqrt{D\left({{\bf{q}}}\right)}\right)\sqrt{D\left({{\bf{q}}}\right)}={\nabla }_{{{\bf{q}}}}D\left({{\bf{q}}}\right)$$
(3)

so that the complicated symbolic manipulation simplifies to a numerical equation, which significantly reduces the computational complexity even when the unit cell is large.

The coherence thermal conductivity scales as \({\kappa }_{C} \sim \frac{\Gamma }{4\triangle {\omega }^{2}+{\Gamma }^{2}}\), where \(\triangle \omega\) represents the scale of separation between phonon branches. When the phonon branch separations are much smaller than the broadening \(\Gamma\), the coherence contribution scales as \({\kappa }_{C}\, \sim \frac{1}{\Gamma }\), while when the broadening \(\Gamma\) is negligible compared to the phonon branch separation, \({\kappa }_{C} \sim \Gamma\). Specifically, for each \({{\boldsymbol{q}}}\) and every two phonon branches, the resonance occurs at \(\delta \omega \left({{\boldsymbol{q}}}\right)=2{\Gamma }_{{\!\!Total}}({{\boldsymbol{q}}})\), where \(\delta \omega \left({{\boldsymbol{q}}}\right)\) is the line separation between the two phonon branches, and \({\Gamma }_{{\!\!Total}}({{\boldsymbol{q}}})\) is the total linewidth by including broadening from both third and fourth-order interactions. It is worth mentioning that the quantum coherence of phonons is analogous to electronic Zener tunneling, in which electrons undergo quantum-mechanical inter-band transitions56 and exhibit resonance behavior.

Interatomic bonding

To obtain the COHP bonding curves, we projected the delocalized planewave basis set used within VASP onto a suitable localized basis set consisting of pseudo-atomic orbitals. The projections were quite computationally demanding for our large 250-atom supercells, so we provide calculations for three temperatures and one chosen configuration for each temperature. Each configuration was chosen such that the average force, maximum force, and average displacement all increased with temperature to ensure that the results reflected the intended change in temperature. We used the LOBSTER code57,58 to perform the basis set projection. We found the default localized basis set provided with LOBSTER to work well in this application, with a calculated charge splashing of only 1%, a low value indicative of a high-quality local basis set projection.