Introduction

Spin dynamics in antiferromagnets (AFM)1,2 has much shorter timescale than that in ferromagnets (FM), offering attractive properties for potential applications in ultrafast devices3,4,5,6. The frequency of typical antiferromagnetic dynamics falls into the terahertz (THz) region5, which is critical for developing the AFM-based oscillator1 in spin-based nanoscale devices7,8. It is generally considered that the spin-torques are used to drive the oscillations of magnetic moments in nano-oscillators, with an a.c. voltage signal as the read-out. The d.c. current is reported to trigger magnetic moment oscillations of gigahertz (GHz) frequency in FM layered structures9,10,11. However, using a d.c. current to excite antiferromagnetic moment oscillation and obtaining an a.c. voltage output in AFM-based structures have not been realized so far, as it is extremely difficult to detect a THz signal by pure electrical methods. In this regard, femtosecond laser pulse is expected to be a more promising tool to excite and detect the antiferromagnetic moment oscillation7,12,13. The optical generation, manipulation and pump-probe detection of THz spin dynamics in bulk AFM have been widely reported14,15,16. It has also been reported in thin film structures, THz electric field is used to exert Néel spin-orbit torque in Mn2Au thin films, and a precession of the Néel vector in the sample plane at 0.6 THz is probed by optical pulse17. Recently, the THz oscillation signal has been experimentally confirmed in antiferromagnetic insulator/heavy metal bilayers through THz emission spectroscopy18. However, the THz oscillation is excited by laser-induced heating, where the repetition frequency is restricted by the cooling time, limiting the potential applications considerably19. Here, we illustrate a non-thermal method to radiate THz oscillations via optical spin-orbit torque (oSOT), which has a profound significance for the development of low-dissipation and controllable AFM-based spin-torque oscillators.

Results

The circularly polarized light generates out-of-plane spin-polarized electrons (σz) in the conduction band due to the optical selection rules for dipole transitions20, and the spin-polarized electrons induce a spin torque which drives the magnetic moment oscillation21,22. In AFMs with local inversion symmetry breaking, such as CuMnAs and Mn2Au, Néel spin-orbit torques can be used to switch the magnetization in a single AFM film without the assistance of heavy metals23,24,25,26. Due to the local inversion symmetry breaking, a current induces opposite spin polarization at two sublattices, leading to the coherent switching of antiferromagnetic moments. Accordingly, antiferromagnetic moment oscillation is expected to occur in AFM driven by SOT, and a charge current can be generated via the spin-to-charge conversion in AFM with local inversion symmetry breaking. In this work, we experimentally demonstrate that the antiferromagnetic moment oscillation with frequency as high as 2 THz can be driven by oSOT in Mn2Au single layer. The oscillating signal can be detected when the direction of the THz detector is parallel to the direction of the antiferromagnetic moment. The spin polarization converts into an a.c. charge current due to the local inversion symmetry breaking and radiates THz electric field in free space. When the direction of the THz detector and antiferromagnetic moment are perpendicular to each other, the emitted THz signal is excited by the thermal effect of the laser and there is no antiferromagnetic moment oscillation signal.

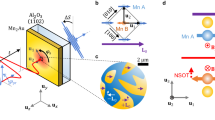
We demonstrate the ultrafast a.c. charge current generation in 15 nm Mn2Au thin films utilizing THz emission spectroscopy technique27,28,29. The Mn2Au film is (103)-oriented and grown on 0.5-mm-thick Pb(Mg1/3Nb2/3)0.7Ti0.3O3 (PMN-PT) (011) substrate25. A commercial Ti:sapphire laser (central wavelength of 800 nm, pulse duration of 100 fs, repetition rate of 1 kHz) is used for THz emission measurements, and the schematic of measurement setup is shown in Fig. 1a (Supplementary Note 1). The x- and y- component of THz electric field can be described as ETHz,x\(\hat{{{\bf{x}}}}\) and ETHz,y\(\hat{{{\bf{y}}}}\) (\(\hat{{{\bf{x}}}}\;{{\rm{and}}}\;\hat{{{\bf{y}}}}\) are the unit vectors along the x- and y- axis in the laboratory coordinate system), respectively. The circularly polarized laser pulses are used as a pump that propagates along the z-axis, and the sample is arranged perpendicular to the z-axis. The Néel vector n (parallel to antiferromagnetic moments) is parallel to \(\hat{{{\bf{x}}}}\) in the original state. Figure. 1b shows that the emitted electric field ETHz,y does not change sign upon the circular polarization reversal. This phenomenon indicates that the THz signal generation is related to the laser-induced thermal absorption effect16 and independent of the circular polarization of the laser. In comparison, the amplitude of THz signal in 15 nm FeRh30 without local broken inversion symmetry is negligible (Supplementary Note 2). It suggests that the non-vanished charge is generated in Mn2Au due to the local broken inversion symmetry. There is no obvious influence on the THz signal when a magnetic field (around 1 T) is applied, which is quite characteristic for antiferromagnetic Mn2Au (Supplementary Note 3). Obviously, Fig. 1c presents that the emitted THz electric field ETHz,x changes sign upon the reversal of the chirality. The spin polarization σz is generated by the circularly polarized laser and is converted into a charge current parallel to Néel vector n via the antiferromagnetic inverse spin Hall effect (AFM-ISHE)31.

Fig. 1: Experimental setup and THz spectrum.
figure 1

a The schematic of THz emission spectroscopy. The antiferromagnetic moments of Mna (red ball) and Mnb (blue ball) align in the (103)-surface. The circularly polarized laser pump propagates along the z-axis and sample is set in the x-y plane, left circular laser: + σ (red line) and right circular laser: – σ (blue line). Néel vector n (purple arrow) is parallel to x-axis in the origin state. The spin polarization + σz (red arrow) and – σz (blue arrow) represent the effective magnetic fields induced by left-handed + σ and right-handed – σ circularly polarized pumps, respectively. Temporal THz waveforms of ETHz,y and ETHz,x from 15 nm Mn2Au single layer upon circularly polarized laser are shown in (b) and (c).

Full size image

In particular, THz waveforms exhibit additional features in the form of oscillations in the longer delay time (as highlighted in the gray shaded part in Fig. 1c). A comparison of terahertz waveforms between ETHz,x and ETHz,y in the left circular laser pulse (+ σ) case is displayed in Fig. 2a. In contrast to the THz waveform of ETHz,y, the signal of ETHz,x shows a distinct oscillation E2 in a longer timescale, which is about 18% of the E1 amplitude for Mn2Au thin films. Since the generation mechanism of the response E1 (both in ETHz,y and ETHz,x) has been illustrated above. The oscillation response in ETHz,x and its absence in ETHz,y suggest that laser-induced heating absorption cannot be the driving force of a detectable antiferromagnetic moment oscillation, while the circularly polarized laser induced oSOT contributes to the oscillation. The difference signal shown in Fig. 2b reveals clear oscillations at a frequency of ~2 THz, and the oscillation signal is slightly misaligned, possibly due to the non-ideal polarization of terahertz field induced by the precession of antiferromagnetic moments.

Fig. 2: Terahertz spin oscillation excitation in Mn2Au thin film.
figure 2

a Comparison of the magnetization dynamics in the same sample with ETHz,x (pink curve) and ETHz,y (green curve). The terahertz oscillation excitation, is evident (much more pronounced) for ETHz,x. b The difference signal of the ETHz,x and ETHz,y. c The emitted THz signals in Mn2Au thin films with thickness of 7, 10, 11, and 15 nm. The inset of (c) presents the thickness-dependent THz signals of the difference between ETHz,x and ETHz,y. The oscillation behavior in terahertz signals of different thicknesses show the similar mode. d The oscillation frequency of ~2 THz in Mn2Au single films with different thicknesses, where the thickness of the metallic layer is comparable to the light penetration depth.

Full size image

The THz waveforms of different Mn2Au thicknesses (7, 10, 11 and 15 nm) are displayed in Fig. 2c. Remarkably, all of the samples are performed in the same THz emission spectroscopy setup and display a similar oscillation mode (Supplementary Note 4), illustrated in the inset of Fig. 2c. The oscillation frequency as a function of Mn2Au thickness is plotted in Fig. 2d. The frequency does not change with the thickness variation and remains ~2 THz, distinct from the standing spin wave excited by interfacial SOT32. This reveals the bulk nature of oSOT in Mn2Au, i.e., uniform torque excited a homogeneous eigenmode across the thickness.

To discuss the relationship between the THz oscillation and Néel vector n, we employ ferroelastic strain from the ferroelectric PMN-PT substrate to switch the Mn2Au Néel vector n25. The experimental data of emitted THz signals are summarized in Fig. 3. Figure 3a, b show schematics of non-volatile ferroelastic switching of Néel vector n in PMN-PT/Mn2Au structures. When a positive E+ (+ 4 kV cm–1), which is larger than the ferroelectric coercive field of PMN-PT (011), is applied, n is switched from [100] to [0\(\bar{1}\)1] (parallel to y-axis). In contrast, under a negative E− (– 2 kV cm–1) with the opposite polarity, n is aligned along [100] (parallel to x-axis).

Fig. 3: Relationship between THz signal and Néel vector n.
figure 3

a, b Schematic of ferroelastic strain switching of UMA driven by electric fields in Mn2Au/PMN-PT (011) structure. Néel moments are switched towards the compressive direction of the PMN-PT substrate, [0\(\bar{1}\)1] and [100] axes in (a) and (b), respectively. The inset of (a) shows a representation of the P–E loop, where P, E+ and E− represent the electric polarization, positive electric field (larger than the ferroelectric coercive field) and negative electric field (coercive field), respectively. The radiated THz emission signals in PMN-PT/Mn2Au structures with electric field E+ and opposite circularly polarized laser with ETHz,x (c) and ETHz,y (d). The radiated ETHz,x (e) and ETHz,y (f) signals from PMN-PT/Mn2Au structures with opposite circularly polarized lasers after electric field E− is applied.

Full size image

After applying a positive electric field E+, the emitted THz electric field ETHz,x and ETHz,y with circularly polarized laser pulses are shown in Fig. 3c and d, respectively. The signal ETHz,x detected in the direction perpendicular to n remains the same polarity and shows no oscillation, while the sign change and oscillation of THz waveforms can be observed in ETHz,y (the direction of THz detector is parallel to n). The similar behavior appears when a negative electric field E− is applied as shown in Fig. 3e and f. The experimental results demonstrate that oSOT contributes to the antiferromagnetic moment oscillation and the polarization of THz oscillation signal is parallel to Néel vector n.

Discussion

We finally discuss how the spin torque induce the THz oscillation in Mn2Au single film. Atomistic spin model simulations using VAMPIRE are carried out to get an insight of the dynamics of antiferromagnetic moments in the whole system33 (see the Methods for details). We describe the sublattice magnetizations in AFM by two unit vectors ma, mb and the net magnetization m = (ma + mb)/2. The dynamics of Mn2Au system can be described with Landau-Lifshitz-Gilbert (LLG) equation34.

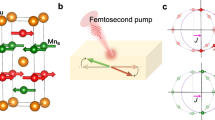
A 100 fs-wide spin-orbit field pulse is applied to the Mn2Au single film. The damping-like part of spin-orbit field is omitted since its tiny proportion compared with the field-like part in single layer system. The two magnetic moments ma and mb are originally arranged along x and –x direction, respectively. When the circularly polarized laser illuminates the sample surface and its chirality induce σz, the two magnetic moments deviate from the equilibrium position, driven by the combination of the field-like torque \({\tau }_{{FL}}={\hat{\sigma }}_{z}\times {{{\boldsymbol{m}}}}_{a,b}\) (parallel to y-axis) and the effective field Heff in Mn2Au. Since the x-y plane [(103)-plane] is not the easy magnetic plane of Mn2Au, a non-zero z-component of Mn magnetic moments can be observed under the effect of the anisotropic field (Fig. 4a). When the circularly polarized laser is removed and the field-like torque vanishes, the two magnetic moments oscillate back to the equilibrium position in 5 ps.

Fig. 4: Atomistic spin modeling of the terahertz spin oscillation in Mn2Au.
figure 4

a The spin polarization σz (green arrow) induced by circularly polarized laser pulse rotates ma (red arrow) and mb (blue arrow) towards y-axis via field-like torque (yellow arrow). ma (mb) oscillates back to the equilibrium in 5 ps once the laser is withdrawn. b The net magnetic moment m possesses an oscillation in y-z plane, and the variation of mx can be neglected. c The calculated terahertz oscillation ETHz,x and ETHz,y in free space.

Full size image

The simulation reveals the oscillating process of Mn magnetic moments in a three-dimensional coordinate system and the calculated oscillation of the net magnetic moment m is shown in Fig. 4b. Taking experimental conditions of thin film systems into consideration, the simulation results show an obvious oscillation signal with a frequency of nearly 2 THz in y- and z- direction but almost no signal along x-direction (Supplementary Notes 6 and  7). The spin polarization along y-direction (net magnetic moment my) converts into an a.c. charge current Jc along x-direction ETHz,x (Fig. 4c) due to the local inversion symmetry breaking of Mn2Au. The dynamics of magnetic moment mx can be negligible, leading to zero terahertz electric field in Fig. 4c (ETHz,y). The results correspond with our experiment measurement, that the THz oscillation signal E2 can only be observed when the THz detector is parallel to Néel vector (parallel to x-direction).

Our work demonstrates the mechanisms of ultrafast THz oscillations in the antiferromagnetic metallic Mn2Au thin films using circularly polarized laser. Unlike magnons generated by optical-induced thermal absorption16, THz oscillation excited by optical spin-orbit torque is thermal-independent. The non-thermal THz emission is explained by the combination of AFM-ISHE and the antiferromagnetic moment oscillation. We also demonstrate that the THz oscillation is directly linked to the intrinsic frequency of Mn2Au, confirmed by the atomistic spin modeling, which provides a key advance to overcome the THz communication gap. In conclusion, our work opens an attractive pathway towards the experimental promise of AFM-based oscillators.

Methods

Thin film growth

The (103)-oriented Mn2Au film is grown on a single-crystal 0.5-mm-thick Pb(Mg1/3Nb2/3)0.7Ti0.3O3 (PMN-PT) (011) substrate by d.c.-magnetron sputter deposition in a 0.4 Pa Ar atmosphere at 573 K from a Mn2Au alloy target (atomic ratio of 2:1). The growth rate is 0.07 nm/s and the base ultrahigh-vacuum pressure is 2.5 × 10−5 Pa. The thin film with thicknesses of 7 nm, 10 nm, 11 nm, 15 nm, 20 nm, 30 nm, and 50 nm is deposited in the same chamber and the same preparation condition.

THz emission spectroscopy

We conducted measurements of THz emission using a commercial Ti:sapphire laser. The main parameters of the laser are as follows: a central wavelength of 800 nm, a pulse duration of 100 fs, and a repetition rate of 1 kHz. The laser beam used for pumping is divided into two parts, with a ratio of 9:1 in terms of intensity. One part is used for photo-generation, while the other is used for electro-optic sampling of the THz spin currents. The chirality-polarized laser pulses are then focused onto the emission samples, with a pot diameter of approximately 3 mm. The laser fluence for the pump beam is 12 μJ mm−2. The emitted THz wave is collected and refocused by two parabolic mirrors with 5 cm reflected focal length. Then, the THz electric field is probed in a 1-mm-thick (110)-oriented ZnTe crystal by measuring the ellipticity modulation of the probe beam. All of the measurements were conducted at room temperature with dry air and the x-component of the THz electric field is measured. For the THz emission experiment, all the samples were kept at the same lattice orientation during the measurement.

Atomistic spin modeling

Atomistic spin model simulations are performed using VAMPIRE, a software dealing with magnetic order parameter of each atom in the whole system. The simulations of the dynamic process of the magnetic moments are based on the spin Hamilton calculating and Landau-Lifshitz-Gilbert (LLG) equation solving. The LLG equation can be described as follow:

$$\frac{\partial {{{\boldsymbol{m}}}}_{a,b}}{\partial t}=-\gamma \left({{{\boldsymbol{m}}}}_{a,b}\times {{{\boldsymbol{H}}}}_{{eff}}\right)+\alpha {{{\boldsymbol{m}}}}_{a,b}\times \frac{\partial {{{\boldsymbol{m}}}}_{{{\boldsymbol{a}}}{{\boldsymbol{,}}}{{\boldsymbol{b}}}}}{\partial t}+\gamma {\zeta }_{{FL}}{\hat{\sigma }}_{z}\times {{{\boldsymbol{m}}}}_{a,b}$$

where γ is the gyromagnetic ratio and α is the Gilbert damping parameter. The spin polarization σz is induced by the chirality-dependent laser pulse and applies the field-like torque on the y-direction. The effective field Heff is given by the anisotropic field and exchange field of Mn2Au, \({\zeta }_{{FL}}\) is the field-like parameter. Therefore, the dynamic process can be obtained once all these factors along with the material system are confirmed.

A Mn2Au crystal model including 1000 cells (10 repeating cells in each dimension) is built in order to carry out the simulations. For the material parameters, we set a Mn atomistic magnetic moment of 3.64 \({\mu }_{B}\), a Gilbert damping factor of 0.01, an easy-plane [(001)-plane] anisotropy of 2.293 meV/atom, an in-plane easy-axis [(100)-axis] anisotropy of 0.017 meV/atom30, exchange interactive energies for the first-, second- and third-neighboring atom pair of −17.075, −22.926 and 4.966 meV/atom. Since the (103)-oriented Mn2Au thin film may have different easy-axis [e.g.(010)-axis], we perform the simulation in this system as well, with an easy-plane anisotropy of 2.333 meV/atom and an in-plane easy-axis anisotropy of 0.017meV25.

The field-like pulse is totally 100 fs in width with 50-fs rising edge and 50-fs trailing edge. The peak strength of the field-like field is 0.01 T. The Mn2Au crystal system is first relaxed for 30 ps to get into equilibrium state. After the 100-fs wide pulse, the calculations are carried out for 30 ps, until the system shows little image of oscillation. A fast Fourier transform of the time evolution is employed to get the frequency of the oscillation.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.