Introduction

2D transition metal dichalcogenides (TMDs) have attracted considerable interest as fascinating quantum materials, exhibiting intricate interplay between charge, spin, and lattice degrees of freedom with strong spin-orbit coupling (SOC)1,2. This unique combination leads to the emergence of multiple intertwined orders with similar energies, giving rise to exotic physics that holds great potential for next-generation quantum devices1,2,3. In particular, the assembly of TMDs into vdWHs offers exciting prospects for realizing unexpected electronic ground states that are not present in the individual constituent layers2,4,5,6,7,8. Some of these states include nematicity, unconventional Ising superconductivity and chiral spin liquids4,6,9,10,11.

Ising superconductivity in TMDs, such as 2H-MoS2, is generally in-plane isotropic12. A few exceptions, such as few-layer 1Td-MoTe2, 2H-NbSe2 and 2M-WS2, possess in-plane anisotropic Ising-like superconductivity13,14,15. The mechanisms underlying this anisotropy have been under debate, with proposals such as anisotropic SOC13, competing superconducting order parameters14 and spin-orbit-parity coupling15. Hence, data from additional in-plane anisotropic Ising superconductors would help to unravel this puzzle. Another important physical effect, the AHE, typically found in magnetic systems with spin-dependent scattering16, in topological materials with nontrivial Berry phase17, or in systems with non-coplanar spin structures18,19, could be an indication of time-reversal symmetry breaking (TRSB). Recent reports of giant extrinsic AHE and TRSB in non-magnetic kagome metals AV3Sb520,21,22,23 and ScV6Sn624,25 suggest the involvement of chiral charge order induced loop currents. Thus, unveiling AHE in non-magnetic systems is of great importance to advancing scientific understanding in this field.

The non-magnetic TMDs 6R-TaS2 represents a promising natural vdWH26,27, with alternating 2D layers of trigonal-prismatic 1H-TaS2 and octahedral 1T-TaS2. Single layer 1H-TaS2 is shown to exhibit SOC-driven Ising superconductivity28 with a conventional s-wave order parameter29,30,31, while single layer 1T-TaS2 is proven to be a correlated Mott insulator hosting a gapless QSL ground state32,33. Below 200 K, single layer 1T-TaS2 undergoes a\(\sqrt{13}\times \sqrt{13}\) charge-density wave (CDW) transition, leading to the formation of a “start-of-David” deformation of the Ta atoms with localized electrons on an emergent frustrated triangular superlattice32,33,34. The electron spins of this superlattice are devoid of magnetic ordering due to strong frustration and quantum fluctuations, creating a QSL5,34 (Fig. 1b). Thus, differently stacked 1H and 1 T layers in the TaS2 family become a fruitful source of exotic physics. Recent spectroscopic studies have revealed Kondo coupling between the itinerant (1H) and the localized (1 T) electrons in MBE grown single layer 1H/1 T heterostructures of TaS2 and TaSe25,8. However, in another natural vdWHs 4Hb-TaS2, Kondo coupling and nematic Ising superconductivity is absent deep in the superconducting state6,35,36,37,38. Furthermore, transport signature of intertwined nematicity and local time-reversal symmetry breaking in 1H/1 T TaS2 vdWHs has been elusive so far.

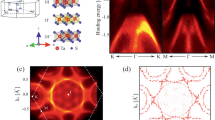
Fig. 1: Natural van der Waals heterostructures (vdWHs), quantum spin liquid (QSL) candidate and nematic Ising superconductivity (SC) in few-layer 6R-TaS2.
figure 1

a Crystal structure of 6R-TaS2 in three different angle views, exhibiting three-fold rotational (C3) symmetry along the c axis with broken inversion symmetry. The blue dashed lines represent a triangular lattice. The black dashed boxes represent a unit cell. b Schematics of a 1 T/1H bilayer comprising one-third of the 6R-TaS2 unit cell. The localized moments in the 1 T layer interacts with the Ising superconducting 1H layer through Kondo coupling (JK) or proximity effect. c Resistivity vs. T at zero magnetic field for 6R-TaS2 device #1 for T from 0.3 K to 360 K. Inset shows the zoom-in view of the superconducting transition. Here, TCDW and \({T}_{c}^{{onset}}\) represents the charge-density-waves transition and superconducting onset transition temperatures, respectively. d Polar plot of angular-dependent normalized in-plane resistance Rab/RN for device #1 under various T near the \({T}_{c}^{{onset}}\) at B// = 5 T, where the magnetic field angle α with respect to x axis ranges from 0° to 360°. Here, B// represents the in-plane magnetic field, and RN represents the normal state resistance at temperatures just above the superconducting transition. e Normalized in-plane upper critical field \({H}_{c2}^{//}/{H}_{{{\rm{p}}}}\) vs. reduced temperature T/Tc along the in-plane directions of α = 90° (solid dots) and 0° (empty dots). The brown dashed line denotes the normalized Pauli limit Hp.

Full size image

In this work, we provide solid experimental evidence of the emergence of a hidden order in 6R-TaS2 thin flakes below a characteristic temperature T* ~ 30 K. Such hidden order simultaneously breaks local time-reversal symmetry and in-plane rotational symmetry, and persists below the superconducting transition temperature. The coexistence of the hidden order with Ising superconductivity produces strongly nematic Ising superconductivity with simultaneous Kondo screening in the 1T-layer. The origin of the nematic Ising superconductivity is narrowed down to anisotropic Ising SOC13, unconventional mixed pairing channels14, or nematicity from the normal state; while the hidden magnetism is attributed to proximity coupling between 1H and 1 T TaS2 layers4,39. Our study provides a platform in the exploration of intertwined physics of nematicity, hidden magnetism and unconventional Ising superconductivity in non-magnetic TMDs vdWHs. A summary of the variety of interesting properties of the TaS2 family with different interlayer coupling can be found in Supplementary Fig. 1.

Results

Nematic Ising superconductivity in thin flake 6R-TaS2

The crystal structure of 6R-TaS2 consists of alternating 1H-TaS2 and 1T-TaS2 layers, which exhibits three-fold rotational (C3) symmetry along the c axis with broken inversion symmetry26 (Fig. 1a). The magneto-transport properties of superconducting and normal state 6R-TaS2 were studied in various sample thicknesses. The device fabrication process and characterization can be found in Methods and Supplementary Figs. 2–6. Three 6R-TaS2 thin flake devices, device #1 (with a thickness of 43.5 nm), device #2 (20.7 nm), and device #3 (7.9 nm), as well as bulk crystals, were investigated.

We found that all the thin flake devices exhibit 2D nematic Ising superconductivity. Data from device #1 is shown in Fig. 1c–e as well as in Supplementary Figs. 7 and 8. Similar data from devices #2 and #3 can be found in Supplementary Figs. 8–11. Figure 1c plots the temperature-dependent resistivity of device #1 at zero magnetic field. Several kinks at around 300 K represent the various CDW transitions of the sample26,27, and the superconductivity transition at around 2 K is shown in the inset. Figure 1d is the polar plot of the normalized in-plane resistance Rab/RN of device #1 from below Tc to above Tc with rotating in-plane magnetic field B// = 5 T, where \(\alpha\) ranges from 0° to 360° is the magnetic field angle with respect to the x axis. Two-fold (C2) nematicity in the superconducting state is evident, with minima of Rab/RN appearing at \(\alpha\) = 90° and 270° and maxima at \(\alpha\) = 0° and 180°. Angular-dependent in-plane upper critical field \({H}_{c2}^{//}(\alpha )\) (Supplementary Fig. 7e) and angular-dependent critical current \({I}_{{{\rm{c}}}}(\alpha )\) (Supplementary Fig. 7f) of device #1 also shows the same nematic behavior of Rab/RN. Furthermore, this anisotropy is pronounced in the superconducting state (\({T < T}_{{{\rm{c}}}}^{{{\rm{onset}}}} \sim 2{{\rm{K}}}\)), while it becomes undetectable at B// ≤ 5 T immediately above \({T}_{{{\rm{c}}}}^{{{\rm{onset}}}}\) (Fig. 1c). The above evidence unambiguously indicates that the two-fold anisotropy arises from nematic superconducting state rather than from resistance anisotropy9.

Figure 1e shows the \({H}_{c2}^{//}/{H}_{{{\rm{p}}}}\) versus reduced temperature T/Tc for α = 0° and 90° in 6R-TaS2 devices #1-#3, where Hp is the Pauli limit. In all the devices, \({H}_{c2}^{//}\) exceeds the Pauli limit for both B// directions, demonstrating nematic Ising superconductivity in the materials. The in-plane anisotropy obtained from \({H}_{c2,\max }^{//}/{H}_{c2,\min }^{//}\) ranges from ~2.6 to 6.5, which is much larger than previous results of Ising-like superconductors13,14,15. Additionally, nematic behavior is observed throughout the superconducting state of 6R-TaS2, in contrast to the isotropic behavior observed in the ultra-low T regime of another vdWHs 4Hb-TaS26. We have ruled out trivial origins of the C2 behaviors, including current induced vortex motion40, strain stress and misalignment of magnetic field (details in Supplementary Figs. 13, 14), leaving the only possibility of nematic Ising superconductivity. Together with evidence shown later in the text, we argue that this state emerges with the hidden order formed at the normal state of the material.

Nematicity and hidden magnetism below T * ~ 30 K

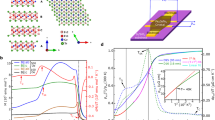
Above the superconducting temperature and below the CDW transition temperature, a hidden order is found in 6R-TaS2 below T* ~ 30 K, which is characterized by the concurrent emergence of nematicity and hidden magnetism. Figure 2a shows the derivative resistance (dRab(T)/dT) of device #1 at zero magnetic field, exhibiting an abrupt change at around 30 K. Figure 2b presents the longitudinal MR of device #1 under 14 T of out-of-plane magnetic field B⊥, together with the two-fold anisotropic MR (AMR = ΔR/Rmin(α)) under 14 T of in-plane magnetic field B//. Although MR and AMR are from completely different measurement configurations, we found that they could be easily scaled together, and both exhibit an upturn at around 30 K. Figure 2c plots the Hall resistivity of device #1 at various temperatures from 3 K to 80 K, with nonlinear Hall curves apparent at low temperatures. Since such nonlinear Hall curves mainly exhibits two sections with different slops (Hall resistance RH), we plot RH of the low and high magnetic field regions in Fig. 2d, where a bifurcation of the two RH is found below T* ~ 30 K. Figure 2e shows the anomalous Hall conductivity σAHE versus temperature, which again exhibits an upturn below T* ~ 30 K. Figure 2f depicts σAHE insensitive to the angles θ between the magnetic field and the c-axis (up to 75° for T = 8 K, and > 45° for T = 21 K and 25.5 K), proving that the observed signal is indeed AHE20,21. Similar data from devices #2, #3 and #bulk can be found in Supplementary Figs. 18–20.

Fig. 2: Hidden order with intertwined physics of nematicity, anomalous Hall effect (AHE), and magnetic field-tunable thermal hysteresis around T* ~ 30 K for device #1.
figure 2

a T-dependent derivative in-plane resistance (dRab/dT) at zero magnetic field, showing an abrupt change at around T* ~ 30 K. Inset shows measurement configuration, with the S and D represents source and drain electrode, respectively. b T-dependent longitudinal magnetoresistance (MR) under B⊥ = 14 T (extracted from Supplementary Fig. 15) and anisotropic magnetoresistance (AMR) under B// = 14 T (extracted from Supplementary Fig. 16), exhibiting a concurrent upturn at T* ~ 30 K. Here B⊥ represents the vertical magnetic field. c Hall resistivity \({\rho }_{{xy}}\)(B⊥) at various T from 3 K to 80 K, with nonlinear Hall curves apparent below T* ~ 30 K. Inset shows measurement configuration. d T-dependent Hall coefficient\({R}_{H}\equiv {d\rho }_{{xy}}/{dB}\) extracted from both low and high magnetic field regions, exhibiting a bifurcation below T* ~ 30 K. e T-dependent anomalous Hall conductivity \({\sigma }_{{{\rm{AHE}}}}\) (main panel) and magnetic field-dependent \({\sigma }_{{{\rm{AHE}}}}\) (inset) at various T, exhibiting an upturn in \({\sigma }_{{{\rm{AHE}}}}\) below T* ~ 30 K. The Hall conductivity\({\sigma }_{{xy}}={-\rho }_{{xy}}/({\rho }_{{xx}}^{2}+{\rho }_{{xy}}^{2})\), then \({\sigma }_{{{\rm{AHE}}}}\) obtained by subtracting the local linear ordinary Hall conductivity background. Here \({\rho }_{{xx}}\) is the longitudinal resistivity. f \({\sigma }_{{{\rm{AHE}}}}(\theta )/{\sigma }_{{{\rm{AHE}}}}(0^{\circ} \; )\) vs. θ, where θ is the angle between the magnetic field and the c axis under various T (extracted from Supplementary Fig. 17). Inset shows measurement configuration. g–i Magnetic field-tunable thermal hysteresis. g T-dependent resistance with decreasing and increasing T under B⊥ = 0 T and 8 T. Inset is a zoom-in plot of the thermal hysteresis at zero field. h T-dependent ΔR (difference in resistance between warming and cooling ramps), exhibiting the temperature range (between ~11 K to 30 K) of the thermal hysteresis. i B⊥-dependent integral area of the hysteresis loop and B⊥-dependent longitudinal MR at T = 15 K (extracted from Supplementary Fig. 21). The loop area is clearly independent of the MR.

Full size image

To our knowledge, no AHE has been reported in other non-magnetic TMDs. And the AHE in 6R-TaS2 is not associated with a CDW transition, in contrast to the CDW-induced AHE in non-magnetic kagome metals AV3Sb520,21 and ScV6Sn625. Furthermore, below T* ~ 30 K, a magnetic field-tunable thermal hysteresis loop (tunable by magnetic field up to ~20% and independent of the MR) is observed in the normal state resistance curve (Fig. 2g–i and Supplementary Figs. 21 and 22), suggesting a first-order phase transition which is not associated with conventional structural transitions, but rather, with an electronic symmetry breaking process arising from orbital41,42,43 or spin44,45 degrees of freedom. Indeed, there has been no report of structural or conventional magnetic phase transitions in 6R-TaS2 ~30 K26,27,46,47,48. The above results unveil a hidden order with intertwined nematicity and hidden magnetism below T* ~ 30 K in 6R-TaS2. The coexistence of the hidden order with Ising superconductivity produces strongly nematic Ising superconductivity with simultaneous Kondo screening in the 1T layer.

Giant extrinsic AHE and Kondo resonance in 6R-TaS2

AHE reflects the anomalous transverse velocity of charge carriers via extrinsic (side-jump or skew-scattering) and intrinsic mechanisms16. Figure 3a plots \({\sigma }_{{{\rm{AHE}}}}\) versus \({\sigma }_{{{\rm{xx}}}}\) of device #1, #2, and #3 together with data from other materials in the literature, spanning over the side-jump (\({\sigma }_{{{\rm{AHE}}}}\propto {\sigma }_{{xx}}^{1.6}\)), intrinsic (\({\sigma }_{{{\rm{AHE}}}}\propto\) constant), and skew-scattering (\({\sigma }_{{{\rm{AHE}}}}\propto {\sigma }_{{xx}}\)) regimes16. The linear dependence of \({\sigma }_{{{\rm{AHE}}}}\) versus \({\sigma }_{{xx}}\) is not obvious with a log-log scale in Fig. 3a, and can be clearly seen in Fig. 3b with a linear scale, similar to previous results in MnGe19, gated CsV3Sb549 and doped Fe16,50, pointing to the extrinsic skew-scattering origin16,19,49,50. Note that AHE is rarely found in non-magnetic materials, with limited examples such as kagome metals AV3Sb5 and ScV6Sn6 (chiral-CDW effects)20,21,25, Weyl semimetal ZrTe5 (Berry curvature effects)17, and 6R-TaS2 in this work.

Fig. 3: Extrinsic AHE with linear scaling relation and Kondo resonance in non-magnetic transition metal dichalcogenides (TMDs) 6R-TaS2.
figure 3

a Map of AHE (\({\sigma }_{{{\rm{AHE}}}}\) vs. \({\sigma }_{{xx}}\)) for various materials in double logarithmic coordinates, spanning over the side-jump (\({\sigma }_{{{\rm{AHE}}}}\propto {\sigma }_{{xx}}^{1.6}\)), intrinsic (\({\sigma }_{{{\rm{AHE}}}}\propto\) constant), and skew-scattering (\({\sigma }_{{{\rm{AHE}}}}\propto {\sigma }_{{xx}}\)) regimes. The solid lines are the linear fitting of \({\sigma }_{{{\rm{AHE}}}}\) vs. \({\sigma }_{{xx}}\) for 6R-TaS2 device #1, #2 and #3. The dashed line is the linear fitting of \({\sigma }_{{{\rm{AHE}}}}\) vs. \({\sigma }_{{xx}}\) for MnGe19. b The linear dependence of \({\sigma }_{{{\rm{AHE}}}}\) vs. \({\sigma }_{{xx}}\) for 6R-TaS2 samples with a linear scale. c T-dependent dI/dV spectrum of the 1H layer at zero magnetic field (Vs = −5 mV, I = 400 pA). d Zero-field scanning tunneling spectroscopy (STS) of the superconducting gap at T = 0.3 K and atomically resolved topography of the 1H layer (inset). The red dot shows the location where the STS spectra were measured. e Kondo resonance in the 1 T layer from 0.3 K (superconducting state) to up to 12 K (normal state) (Vs = −50 mV, I = 400 pA). f Kondo resonance of the 1 T layer at T = 0.3 K. Inset shows scanning tunneling microscopy (STM) topography of the 1 T layer with the \(\sqrt{13}\times \sqrt{13}\) charge-density-wave (CDW) pattern. The red dot shows the location where the STS spectra were measured.

Full size image

In order to elucidate the origin of AHE, we performed scanning tunneling spectroscopy (STS) on 6R-TaS2 bulk crystals with 1H and 1 T termination at temperatures ranging from 0.3 K to 12 K. The STS spectra on the 1H termination (Fig. 3c, d) reveal a normal metal to superconductor phase transition at ~2.5 K with a V-shaped nodal-like pairing gap Δ ~ 0.53 meV, proving 6R-TaS2 as a strong-coupling superconductor (2Δ/kBTc ~ 4.7), in contrast to 4Hb-TaS2 as a weak-coupling superconductor (2Δ/kBTc ~ 3.2)11,35,37. More interestingly, no clear superconducting gap is found in the 1 T termination (Fig. 3e, f), while Kondo screening emerges on each of the CDW centers below ~12 K (normal state) and persists down to 0.3 K (deep inside the superconducting state). The Kondo resonance in 6R-TaS2 is due to the screening of the localized spins on the CDW sites by the metallic 1H layer underneath5, possibly constituting a Kondo lattice like the artificial 1H/1 T heterojunctions5, which is further supported by the spatial dI/dV spectroscopic mapping of Kondo resonance at 4.2 K and 0.3 K (Supplementary Figs. 26 and 27). The quantitative analysis of Kondo resonance and Kondo coupling JK can be seen in Supplementary Fig. 25.

Based on all the findings presented above, we propose that spin-dependent coupling between the 1 T and 1H layers in 6R-TaS2 induces the unconventional hidden magnetism in 6R-TaS2 below T*; the spin state of the QSL in the 1 T layer may be significantly altered, i.e., the highly fluctuating spins may acquire additional broken symmetries akin to the chiral spin liquid phase4,18,51,52. It serves as magnetic scattering impurities without overall net magnetization, giving rise to the large extrinsic AHE in the normal states and hidden magnetism persisting down to the superconducting state in 6R-TaS2.

Phase diagram of nematicity, hidden magnetism and Ising SC

A global phase diagram of the nematicity, hidden magnetism and unconventional Ising superconductivity in 6R-TaS2 crystals is constructed with our experimental findings (Fig. 4a). The phase diagram can be divided into three regions: the isotropic region (gray color), the nematic normal state region with hidden magnetism (blue color), and the nematic Ising superconductivity region with Kondo screening (red color). The first region starts from high temperature down to 30 K, where the crystal is effectively featureless after the CDW transitions at ~305 K, with isotropic in-plane MR (anisotropy <0.5%) down to 30 K. The second region is the normal state below T* ~ 30 K, where nematicity and hidden magnetism emerge simultaneously. Here nematicity is characterized by in-plane AMR as defined in Fig. 2b; hidden magnetism is characterized by 1) large extrinsic AHE under B⊥, 2) magnetic field-tunable thermal hysteresis and 3) Kondo screening as shown in Figs. 3 and 4. The third region is the nematic Ising superconductivity coexisting with Kondo screening at the lower left corner of the phase diagram, defined as the resistivity of the sample below 90% of normal state resistivity RN (purple dots in Fig. 4a), under temperature-dependent critical in-plane fields along α = 90°. Since the orientation of the nematicity is the same for the normal state and the superconducting state, we can conclude that nematicity of the hidden order coexist with Ising superconductivity and substantially modified the superconducting gap in different in-plane directions, producing up to ~10,000% of anisotropy in resistivity. More intriguingly, when a small out-of-plane magnetic field is applied to suppress the superconductivity, the AHE effect is immediately visible without any intermediate state (Supplementary Fig. 28), together with the Kondo screening detected by STS below the superconductivity temperature, proving the coexistence of hidden magnetism and nematic Ising superconductivity in the material.

Fig. 4: Phase diagram of nematicity, hidden magnetism and Ising superconductivity in 6R-TaS2.
figure 4

a B// - T phase diagram of 6R-TaS2 (device #1), divided into three regions: the isotropic region (gray color), the weakly nematic with hidden magnetism region (blue color), and the nematic Ising superconductivity with hidden magnetism region (red color). The purple dots are the boundary between nematic Ising superconducting state and weakly nematic normal state, representing the upper critical field along \(\alpha\) = 90° determined by the 90% RN criterion (extracted from Supplementary Fig. 6g). The yellow ribbon around T* is the boundary between the weakly nematic and isotropic normal state regions. The color scale represents nematicity defined as \([{R}_{\max }(\alpha )-{R}_{\min }(\alpha )]{/R}_{\min }\)(\(\alpha\))(%) and extracted from the AMR (See Supplementary Fig. 16). b–d The representative in-plane AMR curves R(\(\alpha\)) at 5 K and 10 T (blue color region), 1.6 K and 2 T (red color region), 40 K and 10 T (gray color region), respectively. e In-plane AMR curves at 5 K measured with B// from 1 T to 14 T.

Full size image

Some key points are worth noting from the phase diagram (Fig. 4a). First, the hidden phase in 6R-TaS2 (T* ~ 30 K), driven by the particular coupling between the 1 T and 1H layers in the 6 R phase, is different from the spin liquid phase proposed in bulk 1T-TaS2 which persists up to 200 K32,33,34; Second, 6R-TaS2 is the first material in the TaS2 family to exhibit an AHE, which interestingly echoes with theoretical prediction of AHE in triangular lattice systems with Kondo coupling of itinerant electrons and a chiral spin texture53; Third, both the nematic normal state and nematic Ising superconductivity has never been reported in the TaS2 family, which are absent in both the single layer 1H-TaS228 and in ultra-low temperature limit of superconducting 4Hb-TaS26. Fourth, the coexistence of superconductivity and Kondo resonance in 6R-TaS2 has not been observed in either the artificial 1H/1 T heterojunctions5 (without SC gap on its 1H layer) or the natural vdWHs 4Hb-TaS2 (without Kondo resonance on its 1 T layer)36. We argue that although Kondo coupling may occur in all cases (Supplementary Fig. 1), subtle differences in the coupling can lead to large variation in the spin states of the 1 T layer as well as the electronic nematicity in the 1H layer, leading to marked differences in the QSL phases and other exotic physics. Thus manipulating interlayer stacking/coupling of vdWHs may help to construct customizable quantum systems with promising properties (Supplementary Fig. 1)54. Fifth, we note that the origin of the hidden magnetism in 4Hb-TaS2 is still under debate, including theoretical mechanisms related to CSL52, vison-vortex nucleation with ℤ2 topological order55, and type-II heavy Fermi liquids56. For 6R-TaS2, we cannot rule out these three possible mechanisms for the origin of hidden magnetism, as the complex interactions between the 1H and 1 T layers may lead to various possibilities for the spin state of 1 T. On the other hand, nematicity57 has been observed both in the normal state of cuprates58, iron-based59, kagome superconductors60, as well as in the superconducting state of magic-angle graphene9, doped Bi2Se361 and NbSe214. Although the microscopic origin is still unclear, nematicity may coexist, cooperate, or compete with other orders9,57,62. The discovery of a nematic electronic state and hidden magnetism in the normal phase 6R-TaS2 that cooperate with the Ising superconductivity points to the unconventional nature of this hidden order in the material.

Discussion

In conclusion, a hidden order is found in 6R-TaS2 below T* ~ 30 K that is characterized by simultaneous emergence of nematicity and hidden magnetism. The development of hidden magnetism may be related to significantly altered QSL state which acquire additional broken symmetries. Magneto-transport and scanning tunneling spectroscopy data strongly suggest a coexistence of hidden magnetism and nematic Ising superconductivity in 6R-TaS2. The entangled physics of unconventional nematic Ising SC, strong-coupling SC, hidden magnetism, Kondo screening, and \(\sqrt{13}\times \sqrt{13}\) CDW in 6R-TaS2 may provide a fertile ground for the exploration of pair density waves63,64, chiral superconductivity11, Yu-Shiba-Rusinov (YSR)–like bound states7, spin triplet superconductivity65 and more. This work unveils the potential of natural van der Waals heterostructures as a promising platform for exploring the intertwined and exotic physics.

Methods

Single crystals growth

Single crystal samples of 6R-TaS2 have been prepared by phase transition of 1T-TaS2 to 6 R at 800 °C in an inert atmosphere26,27. The pure 1T-TaS2 single crystals were firstly synthesized by the chemical vapor transport (CVT) method using the raw materials of tantalum powder (99.9%,) and sulfur powder (99.999%), combined in a molar ratio of 1:2. Meanwhile, the transport agent iodine spheres (99.99%) weighing 0.25 g/cm3 were placed into a crucible. Then, the crucible was sealed in a quartz tube under a high vacuum (pressure below 10−5 Torr). This assembly was then placed in a two-zone furnace with 1274 K for the end containing the mixture and 1224 K for the growth end. After about 200 h, the quartz tube was rapidly quenched into ice water. Then 1T-TaS2 single crystals can be obtained. At last, the 1T-TaS2 single crystals were further heated at 800°C in evacuated quartz tubes to obtain the 6R-TaS2 single crystal samples.

Single crystals characterizations

The sample has been characterized by diffraction (XRD) studies in θ–2θ geometry using lab-based sources. A Quantum Design Magnetic Property Measurement System (MPMS-3) was used to measure the temperature- and field-dependent magnetization of the samples. The thickness of the various samples was measured using Atomic Force Microscopy (AFM).

Device fabrication

Al2O3-assisted exfoliation technique was used to obtain thin flakes of 6R-TaS2 crystals with a thickness of down to 7.9 nm (more details in Supplementary Fig. 3). Standard e-beam lithography was used to pattern electrodes, followed by e-beam evaporation of Ti (5 nm) and Au (100 nm). The device fabrication process was carried out in an inert atmosphere and vacuum to minimize sample oxidation, and samples were briefly exposed to air only under PMMA capping layer protection. More details of device fabrication process can be found in Supplementary Fig. 4.

Transport measurements

Transport measurements were conducted at temperatures between 0.3 K and 360 K with magnetic fields up to 14 T using an Oxford Teslatron cryostat and a Quantum Design PPMS. Lock-in amplifiers were used to measure longitudinal resistance (Rxx) and Hall resistance (Rxy) at a frequency of 17.77 Hz with an AC current of 10 μA for nano-devices and 2 mA for the bulk devices. Changing the magnetic field direction was achieved by rotating the sample holder. To eliminate the influence of the slight Hall signals on the raw data of angular dependence of resistivity, the resistivity taken at every angle has been averaged with positive and negative magnetic fields. The in-plane resistivity was measured by the standard four-electrode method. Additionally, the c-axis resistance for the bulk sample was measured by the four-electrode method with the Corbino-shape-like configuration. Various resistivity/resistance quantities have been used in this experiment, and their definitions are summarized in the following: Rab represents the resistance in the ab plane, Rc is the out-of-plane resistance, Rxx and Rxy represent longitudinal resistance and transverse Hall resistance, respectively; while ρxx and ρxy represent longitudinal resistivity and transverse Hall resistivity, respectively.

STM/STS measurements

Bulk 6R-TaS2 samples were cleaved in an ultrahigh vacuum chamber at room temperature, and then immediately inserted into the STM head for further topography and spectrum measurements in continuous ultrahigh vacuum. STM measurements were performed using PtIr tips that were well-calibrated on Au(111) surface. All the dI/dV spectrum were taken using the standard lock-in technique (frequency f = 973 Hz) with a small AC modulation (Vmod = 0.05 mV) added to the DC bias.