Introduction

Since the discovery of monolayer magnets by magneto-optical methods, there has been a tremendous surge of interest in 2D magnetic materials in recent years1,2,3,4,5,6,7. These studies have led to the discovery of novel physics phenomena, such as correlated-electron physics8,9, ferromagnetic-superconducting transitions10, and magnon topology11. These discoveries provide an intriguing platform for the development of innovative spintronic devices and quantum information technologies. Among the various 2D magnets, NiPS3 has emerged as a strongly correlated antiferromagnet with complex interactions among spins, electrons, phonons, and magnons8,9,12,13,14,15. One of its notable features is the observation of an exceptionally sharp emission with an intrinsic linewidth on the order of hundreds of micro-electron-volts in the antiferromagnetic phase16,17,18. Furthermore, the excitonic emission shows a strong correlation with the spin order, suggesting the potential for innovative 2D antiferromagnet-based opto-spintronic devices19. The widely accepted explanation for the origin of this emission is Zhang-Rice excitons, a type of many-body exciton16, which is also theoretically understood using density functional theory recently20,21. However, other systematic studies, both experimental and simulation-based, provide substantial evidence to suggest that the emission may originate from either the intrinsic band structures or defect-bound states in NiPS318,22,23. Additionally, there have been conflicting reports regarding the origin of spin-induced linear polarization of exciton emission16,17,18, which is thought to arise from the spin orientation17 and the ferromagnetic zig-zag chain16,18,22. The controversy surrounding the mechanism of excitonic emission and its coupling to magnetism hinders advanced investigations in 2D magnetism and the development of future opto-magnetic devices24,25,26,27. Furthermore, the optical absorption studies on this excitonic transition reveal its resilience to spectral changes in both in-plane and out-of-plane magnetic fields up to 7 T16. Higher magnetic fields are necessary to amplify magneto-exciton effect, which can even result in the rotation or flipping of spins in 2D antiferromagnetic systems.

Here we conduct a systematic magneto-optical study on 2D antiferromagnetic NiPS3 under high magnetic fields to explore the spin-exciton coupling in the materials. The spin-correlated excitonic emission exhibits clear splitting features with applied magnetic fields in the Voigt geometry, accompanied by the spin rotation within the layer plane. The magnetic-field-dependent spectroscopy and polarization features of excitonic emission are further corroborated by precise simulation of spin evolution. Additionally, we also investigate the magneto-optical response of excitonic emission in the Faraday geometry, reaching up to 31 T. The demonstrated magneto-exciton effect in our study provides a deeper understanding of this new type of excitons and their coupling to spins in 2D NiPS3, and will advance fundamental exploration in the field of 2D magnets.

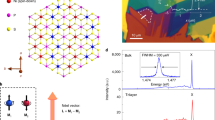
The atomic layers of NiPS3 stack in the C2/m space group, which belongs to the monoclinic crystal system28. When the temperature decreases across its Néel temperature (TN = ~152 K), NiPS3 undergoes a magnetic phase transition and forms a 2D antiferromagnetic XXZ model on a honeycomb lattice (Fig. 1a)12. Each spin is mainly aligned either in parallel or antiparallel along the in-plane a axis, with a slight out-of-plane component resulting in a tilt of the spin from a-b plane at an angle of approximately 7°29. Moreover, the intra-layer spin moments are arranged ferromagnetically in chains along the a axis, but are coupled antiferromagnetically with their neighboring chains. The spin structure of NiPS3 indicates that the a axis of the lattice is the easy axis of the spin structure29,30. Considering the XXZ-type spin structure of NiPS3, the anisotropic energy is small when the spins align along directions within the a-b plane30. Such spin alignment can be achieved by applying in-plane magnetic fields.

Fig. 1: Magneto-exciton effect of NiPS3 with external field direction along a axis.
figure 1

a Top view of lattice and spin structure of an NiPS3 single layer. The crystal orientations (a, b and c axes) are denoted by brown arrows, with the spin orientation primarily along the a axis of the crystal. The black arrow indicates the direction of the applied magnetic field, characterized by the angle θ relative to the a axis of the crystal in the Voigt geometry. b PL spectrum from exfoliated NiPS3 flakes excited by a 532-nm continuous-wave laser at 1.6 K. The sharp excitonic peak is labeled as X, accompanied by two small side peaks labeled as Sα and Sβ. The inset displays an optical microscopy image of exfoliated NiPS3 flakes on a SiO2/Si substrate, with the red point indicating the area where the signal was collected. c Magnetic-field-dependent PL color map of NiPS3 with the external field applied along a axis in the range from −31 to 31 T. d Magnetic-field-dependent PL spectra of NiPS3 with the external field applied along a axis in the range from 0 to 31 T. e Energy shift of the splitting excitonic peaks, X+ (ΔEX+) and X- (ΔEX-), as a function of the magnitude of the applied field. f Full width at half maximum (FWHM) of the excitonic emission as a function of the magnitude of applied field. Error bars represent standard errors from fitting function.

Full size image

NiPS3 flakes were mechanically exfoliated onto SiO2/Si substrates from as-grown bulk single-crystals28. The photoluminescence spectrum of NiPS3 shows a sharp emission (labeled as X) located at ~1.4756 eV with a linewidth of ~270 μeV at 1.6 K (Fig. 1b). The measured sample has a thickness of ~20 nm, as indicated by the atomic force microscopy measurement (Fig. S1). The PL mapping measurement indicates that its line-width is homogeneous on the flakes (Fig. S2), which contradicts the localized emission from an isolated impurity or a single emitter31,32. In addition to the main excitonic peak, two smaller side peaks labeled as Sα and Sβ were observed at 1.4768 and 1.4783 eV, respectively (Fig. S3). The energies of two side peaks are both ~0.5 meV lower than the reported values16, which could due to the sample variance. In contrast, the energy of the excitonic peak X is consistent with the reported values in previous studies16,17,18. An important characteristic of the excitonic emission is its near-unity linear polarization, which has been attributed to the anisotropy of the spin structure16,17,18,33,34. The excitonic emission intensity reaches a maximum when collecting polarization is perpendicular to the a axis17,22. However, within each NiPS3 layer, both the spin orientation and the zigzag ferromagnetic chains align along the a axis and break the three-fold rotation symmetry of the lattice. This results in ambiguity regarding the origin of the linear polarization of X16,17,18,22. It is worth noting that the orientation of spins in 2D antiferromagnets is of significant interest in the community of 2D magnetism, as it plays a crucial role in presenting information in the antiferromagnet-based devices and technologies24,25,26,27. Therefore, these two hypotheses represent distinct underlying physical mechanisms of spin-exciton coupling, which will shape the future development of opto-magnetic and opto-spintronic devices24. One strategy to differentiate the spin orientation from the zig-zag chain direction is to induce spin rotation through external modulations, such as the application of an external magnetic field16,17.

For this purpose, we conducted systematic magneto-optical measurements on NiPS3 bulk crystals in the Voigt geometry. We define θ as the angle between the external field direction and the a axis (Fig. 1a). When the magnetic field is applied along the a axis (θ = 0°), the excitonic peak splits into two branches, labeled as X+ and X-, in the range from −31 to 31 T (Fig. 1c, d). The splitting energy, ΔE = EX+ – EX-, linearly increases with the increase of applied field from 0 to 11 T, reaching a maximum of ~ 2.15 meV. However, when the magnitude of applied field increases above 11 T, the splitting energy drops dramatically and stabilizes at ~0.49 meV (Fig. 1e). The spectral behavior of X implies a wealth of information about the magneto-exciton effect in 2D antiferromagnets. Considering the spin-corrected nature of excitonic emission, we hypothesize that the abrupt change in the splitting energy originates from a field-induced magnetic phase transition from an antiferromagnetic phase to a spin-flop phase35,36. The magnetic phase transition hypothesis is further supported by the field-dependent full width at half maximum (FWHM) of excitonic emission (Fig. 1f). The measured FWHM of X in this set of magneto-optical measurements, even at B = 0 T, is obviously larger than the real value (Fig. 1b), mainly due to the chosen low-resolution grating (see Method section). However, the linewidth still exhibits a clear broadening in the range from 12 to 20 T, suggesting the presence of spin disorder during the magnetic phase transition, which has the same origin as the abrupt change in the splitting energy. In contrast, the original FWHM of excitonic peak at B < 11 T and B > 20 T may suggest a pure magnetic phase. Similar behavior can be also found in the extracted intensity of X (Fig. S4).

Although the spin orientation has been verified to align along the a axis of the NiPS3 crystal29, the XXZ nature of the spin structure still indicates a weak magnetic anisotropy in the a-b plane12,37. To further explore the field-induced energy splitting of the excitonic peak, we conducted series of magneto-PL measurements by applying the magnetic field with the magnitudes ranging from 0 to 12 T, while along different directions in the a-b plane of NiPS3. The energy splitting effect of X from the exfoliated NiPS3 flake exhibits distinct features at various angles (θ) (Fig. 2a). In contrast to the result when θ = 0°, the abrupt change in the spectra is absent with other six θ values from 15° to 90°, where the splitting energy shows a non-linear dependence on the applied field and a gradual variation in the range from 0 to 12 T. The energy splitting effects become inconspicuous as the field direction deviates from the easy axis, and no obvious peak splitting can be observed when the magnetic field is applied along the b axis (i.e., θ = 90°). The FWHM of X+ and X- is set at the same value during the fitting based on their shared origins. A clear broadening is observed from the bulk NiPS3 crystal with an external field up to 31 T along the a axis (Fig. 1f). Another notable characteristic of peak X in the spin-flop phase is the asymmetric behaviors in the peak intensities of the two splitting branches. In most of cases, the intensity of the low-energy branch is weaker than that of the high-energy branch, with an intensity ratio IX-/IX+ below 1. However, the intensity ratio dramatically increases at B > 10 T only when θ = 0° (Fig. S5). Similar results are also observed in another set of magneto-PL study conducted on bulk NiPS3 with magnetic fields ranging from −14 to 14 T in the Voigt geometry (Fig. S6).

Fig. 2: Energy splitting of excitonic emission in the Voigt geometry.
figure 2

a Magneto-optical measurements of exfoliated NiPS3 flakes in the Voigt geometry with the external field applied along different angles within the a-b plane. b Schematic of excitonic energy states in the antiferromagnetic (AFM) phase, featuring the quantum number difference \(\Delta {m}_{s}=\pm 1\) in the transition. c Schematic of excitonic energy states in the canted antiferromagnetic (CAFM) phase, featuring the quantum number difference \(\Delta {m}_{s}=\pm \delta\) in the transition, where δ < 1.

Full size image

The excitonic peak X can be well understood in the framework of Zhang–Rice exciton, which originates from the transition from Zhang–Rice singlet (ZRS) to Zhang–Rice triplet (ZRT) states16. ZRT state represents a state where spin directions at the Ni and S sites are the same, while ZRS state represents a state where spin directions at the Ni and S sites are opposite. The magnetic behaviors of X remain a variety of controversy within the framework of Zhang-Rice exciton. For instance, the spectral features of sharp emission have been reported to be insensitive to the magnetic field, which were considered to conform to the Zhang-Rice exciton nature16. However, a recent study presented a distinct phenomenon: a clear splitting effect of the X transition under in-plane fields38. Contrary to previous perspectives on the robustness of the spectral features of Zhang-Rice excitons, this remarkable response to magnetic fields was treated as clear evidence to rule out the Zhang-Rice picture as the origin38. Unlike the previous viewpoints on the magnetic response of Zhang-Rice excitons, in this work, we argue that the spectral evolution of X peak reveals its nature of singlet-triplet transition, which is consistent with the framework of Zhang-Rice exciton.

When the exciton transitions from singlet to triplet states, the spin orientations experience a spin flip, resulting in a change in quantum number from ms = 0 to ms = ±1 (Fig. S7a, b). Consequently, the triplet state with ms = ±1 splits under the external magnetic field, leading to the splitting of X (Fig. 2b). Meanwhile, with the application of an in-plane magnetic field, the spins rotate in-plane, and the spin structure of NiPS3 changes from the antiferromagnetic to canted antiferromagnetic phases when θ ≠ 0° (Fig. S7c, d). In the canted antiferromagnetic phase, the spin orientations at the Ni and S sites vary in two directions with an angle smaller than 180°. Therefore, the excitonic transition in the canted antiferromagnetic phase results in a quantum number difference Δms = ± δ = ± |M1 – M2 | /2 = ± |L | /2, where M1 and M2 represent two different spin momenta in NiPS3; and L = M1 – M2 is the Néel vector. Considering the antiferromagnetic nature of the spin structure, we assume the magnitude of each spin momentum as unity, i.e., M1 = M2 = 1, and we have δ < 1 in the canted antiferromagnetic phase (Fig. 2c). Compared to the split triplet state with ms = +δ, the ms = –δ state has lower energy and consequent higher carrier density with an application of positive magnetic field, resulting in a preference for transition from singlet and a higher peak intensity of X+ in the region of low magnetic field (Fig. S5). In contrast, the reversed intensity ratio between two splitting branches at B > 10 T and θ = 0° suggests that the energy diagrams described in Fig. 2b, c is no longer applicable under in the case of high applied fields. A stronger peak of low-energy transition potentially indicates a splitting of excited state, and further implies an entirely different energy diagram in the spin-flop phase.

The energy splitting of X branches (X+ and X−) is proposed to be described by the following equation,

$${E}_{{\rm{X}}+/{\rm{X}}-}={E}_{{\rm{X}}0}\pm {g}_{s}{\mu }_{B}B\cos \varphi {\Delta m}_{s}={E}_{{\rm{X}}0}\pm \frac{1}{2}{g}_{s}{\mu }_{B} \, {\bf{B}}{\,{\cdot }}{\, \bf{L}},$$
(1)

where gs ≈ 2.0 is the Landé g-factor for electrons, and φ is defined as the angle between B and L. When θ ≠ 0, with the increase of B, the spin momenta \({{\bf{M}}}_{{\boldsymbol{1}}}\) and \({{\bf{M}}}_{{\boldsymbol{2}}}\) experience an in-plane rotation, which is determined by the competition between super-exchange coupling and magnetic anisotropy constant36 (Fig. 3a). Therefore, φ is also expected to change with the increase of B in the Voigt geometry, resulting in a variation in the splitting energy. Here we define k = gsΔms cos φ to describe the slope of magnetic-field-dependent energy splitting of X. With B = 0, we have φ = θ and Δms = ±1 for the transition from singlet to triplet states. As a result, on the premise that the spin rotation could be neglected at a low field (e.g. B ≤ 4 T), the energy shift of X branches is nearly linearly dependent on the field magnitude for various applied field directions, where k = gs cos θ. Thus, we extract the k values from experimental data using k =ΔE/2μBB under B = 2, 3 and 4 T (Fig. 3b). The values of k match well with the calculated value, where we obtain gs ≈ 1.90 ± 0.02 by fitting. The result indicates that the splitting energy of peak X is determined by the effective field applied along the Néel vector direction.

Fig. 3: Simulated spin evolution in 2D antiferromagnetic NiPS3.
figure 3

a Schematic of spin evolution under an in-plane magnetic field. The blue, red, and orange arrows represent the spin momenta M1, M2, and Néel vector L, with angles φ1, φ2, and φ with respect to the positive direction of the applied field (depicted as a black arrow). b Magnetic-field-direction-dependent k values, which are derived from the experimental data using the formula \(k=\Delta E/2{\mu }_{B}B\). The dashed line represents the fitting line based on \(k={g}_{\text{s}}\cos \theta\). Error bars represent standard errors from fitting function. c Simulated k value as a function of the magnitude B and direction θ of the magnetic field. k is defined as \({g}_{s}\Delta {\text{m}}_{\text{s}}\cos \varphi\). d Simulated energy splitting ΔE as a function of the magnitude B and direction θ of the magnetic field. e Magnetic-field-dependent energy splitting extracted from experimental data by \(\Delta E={E}_{X+}-{E}_{X-}\), compared with calculated results. The experimental data of θ = 0o is compared with calculated data of θ = 2o.

Full size image

In order to quantitatively understand the excitonic transition under an external field, the spin states with a given applied in-plane field, described by B and θ, have been simulated. We consider a two-sublattice antiferromagnet characterized by two macrospin, S1 and S2, which correspond to the magnetic momentums M1 and M2 with unity magnitudes in NiPS3. M1 and M2 are antiparallel when the magnetic field is zero, representing the initial antiferromagnetic phase. The general Hamiltonian of the antiferromagnetic system can be written as36:

$$H=J{{\bf{M}}}_{1}\cdot {{\bf{M}}}_{2}-\frac{A}{2}\left[{\left({{\bf{M}}}_{1}\cdot \hat{x}\right)}^{2}+{\left({{\bf{M}}}_{2}\cdot \hat{x}\right)}^{2}\right]-{g{\mu }}_{B}{\bf{B}}\cdot \left({{\bf{M}}}_{1}+{{\bf{M}}}_{2}\right),$$
(2)

where J is the antiferromagnetic exchange coupling, and A is the easy axis anisotropy with \(\hat{x}\) refers to the easy axis of spin structure. The ground state can be obtained by minimizing the Hamiltonian. In an approximation, we can use this model to simulate the spin structure evolution of NiPS3 under an in-plane field. To simplify the calculation, we convert this equation into a function of three angles θ, φ1, and φ2 (see Methods). φ1 and φ2 are defined as the angles of M1 and M2 concerning the positive direction of the external field (Fig. 3a). The constant k = gs Δms cos φ and splitting energy ΔE = 2kμBB are simulated as a function of B and θ (Fig. 3c–d and Fig. S8). Also, ΔE are extracted from the experimental data in Fig. 2a through ΔE = EX+ – EX–. We compare the experimental results with the calculated values (Fig. 3e). Of particular note, the experimental data with θ = 0° matches better with the simulated curve of θ = 2° (Fig. S9). This minor angle difference may result from experimental errors in aligning the sample’s a axis with the magnetic field direction. For all the directions of the applied field, the simulated results strongly agree with the experimental data at low field region of B < 10 T, while they start to deviate at higher field region. The deviation may be attributed to emergence of complex local spin structures in NiPS3 induced by the high field, causing considerable variations on excitonic energy levels20,39. The small total energy differences among different magnetic configurations at the level of several to tens of meV might be reached by the application of an external field20.

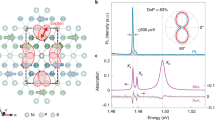
In addition to the spectral features under in-plane fields, the polarization of the excitonic emission also carries rich spin information in NiPS3. Previous studies have reported that the intensity of X is nearly independent of the incident laser polarization but strongly dependent on the collection light polarization16,17,18. The strong coupling between exciton dipole and local spin originates from the spin-flip during the singlet-triplet transition, resulting in the exciton dipole being perpendicular to the spin orientation17. In light of this, we measure the polarization-dependent photoluminescence spectra by rotating the analyzer angle with varying direction (θ) and magnitude (B) of the applied field (Fig. 4a and Fig. S10). Across all configurations, two splitting branches exhibit clear linear polarizations, with the maximal intensity consistently occurring at the same polarization angle (Fig. S11). The polarization angles of both branches further rotate with the increase of the in-plane field (Fig. 4b). The measured rotation of the polarization angle of X can be attributed to two roots: the rotation of the Néel vector induced by the in-plane magnetic field and the Faraday rotation of collection light passing through the objective lens along the magnetic field direction. To exclude the contribution from Faraday rotation, we conduct a controlled experiment described in Methods and Fig. S12. By removing the influence of Faraday rotation, the measured polarization of the X can be used as a probe to determine the Néel vector orientation in NiPS317. The Néel vector orientation can be calculated as φ = φ1 + φ2 + 90°, where φ1 and φ2 are also functions of B and θ (Fig. S13). Notably, the field-dependent polarization angle of the X with different θ exhibits excellent agreement with the simulation results (Fig. 4c), confirming the effectivity of our simulation in capturing both the energy splitting ΔE and the Néel vector orientation φ. This enables us to obtain a detailed understanding of the spin evolution in 2D antiferromagnetic NiPS3, as illustrated by typical spin configurations at various applied magnetic fields (Fig. 4d). Our magneto-optical investigation of the excitonic transition offers a multi-angle approach to study the unique spin-exciton coupling and magnetic behaviors in NiPS3.

Fig. 4: Exciton polarization evolution and spin evolution probe in NiPS3.
figure 4

a Collection-polarization-dependent PL color map with applied fields along the a axis under different magnetic fields at 5 K. b Polar plots of the intensity of X- branch as a function of the collection polarization angle at selected magnitudes of the applied field. In each panel, the black dashed line represents the polar fitting without an external field. The polarization angle of the X- rotates with the increase of magnitude of the applied field. c PL polarization angle of X as a function of the in-plane magnetic field with different θ, compared with calculated PL polarization (labeled with solid curves) by φCal-X = φL + 90°, where φL is the simulated Néel vector direction. The experimental polarization angles are the value after excluding the Faraday rotation effect. The experimental data of θ = 0o is compared with calculated data of θ = 2o. In the four configurations, the applied field direction is along 90o, which is denoted by the black dashed line. Error bars represent standard errors from fitting function. d Simulated spin evolution under magnetic field with different magnitudes B and directions θ. The red and blue arrows represent the spin momenta M1 and M2, respectively.

Full size image

In contrast to the sensitive response of the exciton to the magnetic field in the Voigt geometry, the excitonic emission becomes robust to the field in the Faraday geometry, where the applied field is nearly perpendicular to the spin direction in NiPS3 (Fig. 5a). We notice that X does not exhibit a clear variation at B < 10 T (Fig. 5b), which is consistent with previous results in the literature16. The anisotropy between the in-plane and out-of-plane directions should lead to considerable difficulty in rotating the spins by an out-of-plane field in the present experimental conditions. However, considering the small out-of-plane component of the spin momentum of NiPS3, the magneto-optical response of the excitonic transition is still expected to be observed, even though a strong external field is required. As a result, X exhibits an energy shift of ~ 97 μeV with a quenched intensity at B = 31 T, compared with the case of zero magnetic field (Fig. 5c). Moreover, the field-dependent peak position and FWHM exhibit nonlinear relations (Fig. S14), which are similar to the magneto-exciton behavior of bright excitons in transition metal dichalcogenides in the Voigt geometry40. This similarity suggests that the slight peak shift of X possibly originates from the diamagnetic shift and implies the existence of a dark state at higher energy that coupling with the X state. The X emission energy (EX) can be fitted well using the following formula40,

$${E}_{X}={E}_{X0}+\frac{\Delta {E}_{0}}{2}-\sqrt{{\left(\frac{\Delta {E}_{0}}{2}\right)}^{2}+{\left(\frac{{g}_{F}{\mu }_{B}B}{2}\right)}^{2}},$$
(3)

where EX0 and ΔE0 are the energy of X transition and the energy difference between X and higher dark state without the applied field; \({g}_{F}\) is the Landé g-factor for the transition in the Faraday geometry; \({\mu }_{B}\) is Bohr magneton; B is the magnitude of the applied field. We obtain ΔE0 = ~ 1.5 meV by fitting, which is matches the energy of Sα peak. However, two side peaks from the measured sample cannot be well resolved on the spectra, so we did not observe their field-dependent behaviors to further confirm whether Sα is the dark state for the bright excitonic state. Further investigation is necessary to verify this hypothesis.

Fig. 5: Magneto-exciton effect of NiPS3 in the Faraday geometry.
figure 5

a Schematic of the Faraday geometry with the applied field direction perpendicular to the a-b plane of NiPS3 crystal. The red and blue arrows represent the spin momenta, suggesting the XXZ-type antiferromagnetic spin structure of NiPS3. The black dashed lines represent the honeycomb spin structure, and the gray solid lines show the edge of the unit cell. b Magnetic-field-dependent PL spectra of NiPS3 in the Faraday geometry under 532-nm laser excitation at 5 K. The black dashed line indicates the peak position at B = 0 T for comparison. c Magnetic-field-dependent PL color map of NiPS3 in the Faraday geometry under 532-nm laser excitation at 5 K. The black dashed line represents the fitting curve of the magnetic-field-dependent peak position of X emission.

Full size image

Uncovering the underlying physics of antiferromagnetic spin states, especially in the 2D cases, poses a significant challenge due to the absence of net magnetism41,42,43. In this work, we observed a pronounced magneto-exciton effect in NiPS3, leading to substantial variations in the optical spectra. The exceptional sharp emission exhibits a Zeeman-like splitting under an in-plane magnetic field with a Landé g-factor around 2, providing strong experimental evidence to identify the exciton mode as an excitation of dominant triplet-singlet character. Moreover, the field-induced polarization rotation of exitonic emission is unambiguously proven to be correlated with the Néel vector rotation, which has been further supported by a simulation of spin evolution. Our investigation into the magneto-exciton coupling in NiPS3 sheds light on new facets of magnetism and opto-magnetism at the extreme nanoscale limit. The unique characteristics of antiferromagnets, such as terahertz resonance, multilevel states, and the absence of stray fields, make them highly attractive for spintronic devices. Leveraging the strong correlation between spins and excitons, optical methods could be employed to probe and manipulate the spin orders, paving the way for the further advanced studies to achieve a deeper understanding of fundamental physics in the field of 2D magnetism.

Note: Recently, a related work by Jana et al. appeared, reporting similar magneto-PL results38.

Methods

Sample preparation and characterization

NiPS3 single crystals were grown using a chemical vapor transport (CVT) method28. NiPS3 flakes were mechanically exfoliated onto Si substrates with a 285-nm SiO2 layer from a bulk single-crystal. The morphology and thickness of exfoliated flakes were characterized by optical microscopy (Olympus BX53) and atomic force microscopy (Bruker NW4) in a tapping mode. The crystal orientations (a and b axes) of NiPS3 sample were determined by polarized PL measurements, where the excitonic emission intensity reaches a maximum with collecting polarization along the b axis17,22.

Magneto-optical measurements

The magneto-PL experiments on exfoliated NiPS3 flakes were performed in a closed cycle cryostat (Attocube attoDRY2100). The magnetic field was applied in the Voigt geometry from 0 to 12 T. A 532-nm laser was used to excite the sample. PL signals were collected by a low-temperature objective, propagate in a free beam throughout collecting path, and measured by a spectrometer (Horiba iHR550) equipped with a liquid-nitrogen-cooled charge-coupled device (CCD). A high-resolution 1800g/mm grating was chosen to disperse the PL signal with a spectral resolution of ~70 μeV. The magneto-PL experiments of bulk NiPS3 crystals were performed in a 14 T DC magnet and a 31 T DC magnet in the National High Magnetic Field Laboratory. A 532-nm laser was used to excite the sample. In the Faraday geometry, the sample was horizontal placed in the center of the magnetic cell with the surface perpendicular to the applied magnetic field. In the Voigt geometry, a mirror was set between the objective and the sample with 45° to guide the optical path by 90°, and the sample was vertically placed in the center of the magnetic cell with the surface parallel to the applied magnetic field. A converted 10× objective in the magnetic cell was used to focus the laser beam on the sample and collect the PL signal. Both the incident and collection lights propagate in a free-beam in the magnetic cell. For the polarization-dependent PL measurement, the collected signal was filtered by an analyzer, subsequently collected by a multi-mode optical fiber, and measured by a spectrometer (Princeton Instruments, IsoPlane 320) equipped an electrically cooled CCD. A 1800g/mm grating was chosen to disperse the PL signal in the measurement in the Faraday geometry and a 1200 g/mm grating was selected in the measurement in the Voigt geometry.

Determination of the Faraday rotation of the PL signal

An ideal method to exclude the contribution of Faraday rotation is to conduct a control experiment with θ = 0°, where the Néel vector is considered unchanged before the field-induced phase transition to the spin-flop phase happens17. The Faraday rotation at different applied fields can be obtained by measuring the rotation of the polarization angle of excitonic peak X with θ = 0°. However, accurately aligning the NiPS3 sample with the a axis of the crystal along the direction of the applied field is challenging, the Néel vector will exhibit a considerable rotation (φ) even with a small value of θ, as shown in our simulation (Fig. S12a). The effect caused by the experimental error in θ can be estimated by the simulated value of dφ/dθ. In the range from 0 to 10 T, the value of dφ/dθ is relatively small when θ is around 30°. Therefore, in this work, we mount two samples with θ = 30° and −30°, and measured their polarization rotations of X emission, α1 and α2. In this case, these two samples will have the opposite Néel vector rotation and the same Faraday rotation. Thus, the contribution from the Néel vector rotation due to the small error in sample alignment will be canceled out. We obtain a Faraday rotation φF = (α1 + α2)/2 = ~2.305°/T in this work, which applies to all θ values for the same magnetic cell and optical path (Fig. S12b).

Simulation of spin rotation with the external magnetic field

To calculate the splitting energy with given B and θ, we consider a two-sublattice antiferromagnet featured by two macrospin, S1 and S2, manipulated by in-plane magnetic fields along different angles. S1 and S2 are antiparallel when the magnetic field is zero. The free energy density of two dimensionless vectors m1 and m2 can be written as36:

$$E=J{{\bf{m}}}_{1}\cdot {{\bf{m}}}_{2}-\frac{A}{2}\left[{\left({{\bf{m}}}_{1}\cdot \hat{x}\right)}^{2}+{\left({{\bf{m}}}_{2}\cdot \hat{x}\right)}^{2}\right]-{M}_{S}{{\bf{H}}}_{0}\cdot ({{\bf{m}}}_{1}+{{\bf{m}}}_{2}),$$
(4)

where m1 = S1/S1; m2 = S2/S2; H0 is the external magnetic field; \(\hat{x}\) refer to the easy-axis; J and A are the antiferromagnetic exchange coupling and the easy axis anisotropy, respectively.

We can then simplify the free energy density as a function of three angles:

$$E= \frac{{{\hslash }}}{2}\left[{\omega }_{J}\cos \left({\theta }_{1}-{\theta }_{2}\right)-\frac{{\omega }_{A}}{2}\left({\cos }^{2}{\theta }_{1}+{\cos }^{2}{\theta }_{2}\right)\right] \\ -\frac{{{\hslash }}{\omega }_{H}}{2}\left[\cos \left(\phi -{\theta }_{1}\right)+\cos \left(\phi -{\theta }_{2}\right)\right]$$
(5)

where ℏωJ = J, ℏωA = A, ℏωH = H0Ms; θ1, θ2, and ϕ are the angles of m1, m2, and in-plane magnetic field B to the easy axis. Here we scale all parameters into angular frequencies for calculation. We compensate for the calculated results by multiplying constants to match the experimental data.