Exhaustive local chemical space exploration using a transformer model

Abstract

How many near-neighbors does a molecule have? This fundamental question in chemistry is crucial for molecular optimization problems under the similarity principle assumption. Generative models can sample molecules from a vast chemical space but lack explicit knowledge about molecular similarity. Therefore, these models need guidance from reinforcement learning to sample a relevant similar chemical space. However, they still miss a mechanism to measure the coverage of a specific region of the chemical space. To overcome these limitations, a source-target molecular transformer model, regularized via a similarity kernel function, is proposed. Trained on a largest dataset of ≥200 billion molecular pairs, the model enforces a direct relationship between generating a target molecule and its similarity to a source molecule. Results indicate that the regularization term significantly improves the correlation between generation probability and molecular similarity, enabling exhaustive exploration of molecule near-neighborhoods.

Introduction

The so called similarity principle¹—that structurally similar molecules share similar properties—is a key concept in drug discovery and molecular design. The main challenge in drug discovery is to find compounds with a combination of desirable properties such as absorption, distribution, metabolism, elimination and toxicity, safety, and potency. Molecular optimization aims to address this challenge by exploiting the similarity principle, improving properties of molecules through small changes while still retaining or improving already desirable properties, for example retaining affinity against a drug target while improving aqueous solubility.

The enormous sized “drug-like” chemical space is frequently discussed. One estimation based on the GDB-17 dataset is that the chemical space contains 10³³ compounds². There is no broadly accepted way to quantify how much of this vast space is similar to a given compound of interest, in other words, how dense is the chemical space. Further, although there exist methods that allow for local combinatorial modification of compounds based on reagents^3,4 and based on matched molecular pairs (MMP)⁵, despite the key practical importance of this task, no existing method is currently available that can systematically and exhaustively sample this bespoke chemical space.

In recent years, the application of deep learning methods have had a dramatic impact in the field of chemistry^6,7 and drug discovery^8,9,10. Advances in machine learning, including transformers¹¹, which have already shown remarkable success in natural language processing^12,13 and computer vision^14,15,16, are readily adapted to solve domain-specific problems including molecular design. Many different deep-learning architectures have been proposed to explore the chemical space. Grisoni et al.¹⁷ and Segler et al.¹⁸ proposed recurrent neural networks, De Cao and Kipf¹⁹ investigated generative adversarial networks, and Gómez-Bombarelli et al.²⁰ and Jin et al.²¹ used variational autoencoders to sample new molecules. All of these techniques allow sampling compounds from the chemical space, but they do not naturally encode the localized search characteristic of molecular optimization. The generated molecules need to be refined with e.g., reinforcement learning approaches^22,23 or via coupling the latent representation to a predictive model.

Others²⁴ have been treating molecular optimization as a translation task between a source and a target molecule, inspired by natural language processing (NLP). These source-target-based methods require a dataset of molecular pairs for training. Inspired by the medicinal chemistry concept of matched molecular pairs, He et al.²⁵ generated molecular pairs based on MMP, identical scaffolds, or a Tanimoto similarity above a certain threshold. The set of pairs were used to train different molecular transformer models to explore the region of the chemical space relatively close to a source compound.

A molecular transformer is able to generate the most precedented (probable) molecular transformations from a specific source molecule. The precedence (probability) of generating a molecule is a novel concept not explicitly discussed in earlier work in deep learning-based molecular de novo generation.

Precedence of transformations is determined by the distribution of the observed data (empirical distribution) and, more specifically, by a criterion of pair generation. Given a source molecule, we consider the space comprising all possible transformations that do not violate the criterion used for generating pairs. We define as precedence the empirical data distribution on this space. In our approach, we introduce an inductive bias directing our model away from the empirical data distribution created by pair generation. This is achieved by explicitly adjusting sampling probability through regularization (see Eq. (3)) of negative log-likelihoods (NLLs) to align with a similarity metric rather than solely adhering to the empirical data distribution. We consider auto-regressive transformers with SMILES, which have emerged as powerful paradigm for molecular generation^24,25,26. In this approach, each generated token in the SMILES string is added with a certain probability. Thus each generated molecule (SMILES string) will have a certain probability. A precedented transformation for a given target molecule are those that have high probability to be applied to a given source molecule. The precedence associated to the molecular transformation to a generated target molecule is learnt by the transformer model during the training phase, but the precedence is not necessarily related to the molecular similarity between the source and target molecule, i.e., a transformer model can generate target molecules with a high precedence which are very dissimilar to the source molecule. This behavior is not optimal in applications such as lead optimization where one would like to be able to generate all similar and relevant compounds given a specific source molecule.

Motivated by the fact that aforementioned approaches have only an intrinsic knowledge of the similarity between molecules, given by the way the molecular pairs are constructed, we propose in this paper a framework to systematically sample target molecules that are simultaneously associated to precedented transformations and are similar to the source molecule. We stress the fact that similarity alone is not enough as there exist target molecules similar to a source molecule that should be associated to low precedented transformations, for example chemically unstable target molecules or target molecules containing an unusual atomic element not represented in the training set.

To improve on the existing molecular transformer models, we have developed a source-target molecular transformer model, trained at a large scale on 10¹¹ molecular pairs, that is able to pseudo-exhaustively sample the near-neighborhood, represented by highly precedented transformations and similar target molecules, of a given source molecule. We adopted the same molecular transformer model as proposed by He et al.²⁵ but included a regularization term into the training process to explicitly control the similarity of the generated molecules. This additional term penalizes the generated target molecules if their similarity to the source molecule does not align with their assigned negative log-likelihood (NLL), which is used as a proxy for precedence (probability). However, as discussed in the “Methods” section, the correlation between similarity and precedence will never be perfect, and there will be similar target molecules associated with low precedented transformations. In contrast to several recent works which used ChEMBL²⁷ to train transformer models, we used PubChem²⁸ which contains 40× more molecules, and accordingly many more molecular pairs that can be extracted and used for training. In this study, we retain the similarity principle assumption. Our aim is to develop a versatile model that can produce similar molecules efficiently and fine-tuned using reinforcement learning for task-specific requirements. Incorporating properties into the training set is also an option but it would require to retrain the model as soon as the desiderata properties change.

The main contributions of this work can be summarized as:

• a regularization term in the training loss for the source-target molecular transformer is introduced, which establishes a direct relationship between the precedence (probability, NLL) of sampling a particular target molecule given a specific source molecule and a given similarity metric;

• this method is used to train a foundational molecular transformer model trained on what is, to the best of our knowledge, the largest ever dataset of molecular pairs assembled, comprising of over 200 billion pairs. Some recent source-target models^24,25 used 2 to 10 million pairs, while previous foundational chemical transformer models such as ChemBERTa²⁹ were trained on approximately 100 million unique molecules. Contrastive-learning baselines are available at the 10 million molecule scale³⁰;

• our transformer model allows for the approximately exhaustive sampling by using beam search to identify all target molecules up to a user defined precedence (NLL) level for a given source molecule. This corresponds by construction to an approximately complete near-neighborhood chemical space of similar target molecules with a high precedence for a given source molecule;

• we demonstrated (refer to the section “Generalization of the method” and Supplementary Section 2.1) that our framework is applicable and generalizes to various dataset scenarios, similarity metrics, and models.

All software is based on Python 3.9. The transformer models and software to reproduce our results are available at https://github.com/MolecularAI/exahustive_search_mol2mol.

Results

Four different transformer models on ${\mathcal{D}}$ and ${{\mathcal{D}}}^{c}$ with and without ranking loss were trained and the impact of the regularization term during training and the count version of the ECFP4 fingerprints were evaluated (see Eq. (3) and the section “Model training and sampling” for training details).

Impact of ranking loss for sampling similar molecules

We evaluated all the metrics described in the section “Evaluation metrics” for the 821 compounds in the TTD database. The results in Table 1 clearly show that the binary and count versions perform approximately the same in terms of VALIDITY, UNIQUENESS, and TOP IDENTICAL. The models with regularization term (λ = 10) significantly improve the TOP IDENTICAL, RANK SCORE, and CORRELATION metrics. Finally, the model trained on ${{\mathcal{D}}}^{c}$ with λ = 10 outperforms all the other models on the RANK SCORE, and CORRELATION metrics, showing that the ECFP4 fingerprint with counts achieves superior results compared to the binary version. The models were trained on RDKit canonicalized SMILES strings, however, the transformer models can also generate non-canonicalized valid SMILES strings. The uniqueness after the molecules are canonicalized, remains close to 1.0 in all cases, indicating that in most cases the canonicalized version of the SMILES string is the only one generated. However once stereo-chemical information is removed (NS in Table 1), the uniqueness falls to 0.5–0.6, which suggests that the transformer models are generating approximately two stereo-isomers for most of the target molecules. The increase from 0–0.3 to 0.6–0.9 for TOP IDENTICAL when removing stereo-chemical information indicates that the transformer models generate different stereo-isomers with similar precedence.

Table 1 Combined results for all compounds in the TTD database for beam size B = 1000 and the different transformer models

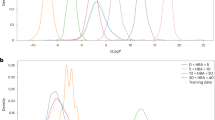
Figure 1 reports the results of the generated compounds corresponding to penicillin. Overall, the ranking score is always higher for the generated molecules from the regularized (λ = 10) models. Furthermore, the distribution of the Tanimoto similarity is always shifted to the right for the λ = 10 case, confirming that the regularized transformer models generate more target molecules similar to a given source molecule. More experiments showing the generality of the approach can be found in Supplementary Sections 2 and 4.

Fig. 1: Similarity (x-axis) and NLL (y-axis) of generated target compounds with penicillin as the source compound (depicted on top).

NLL represents the negative log-likelihood. Top and bottom scatter plots refer to ${\mathcal{D}}$ (fingerprints without counts) and ${{\mathcal{D}}}^{c}$ (fingerprints with counts), respectively. The first two scatter plots from the left show the Tanimoto similarity against the NLL for the λ = 0 and λ = 10 models. λ is the hyperparameter controlling the strength of the regularization term. The CORRELATION, i.e., the Pearson correlation coefficient between the Tanimoto similarity and the NLL, is always better for λ = 10 models. The green line in each scatter plot is the linear fitting of the data points. The plot to the right shows the distribution of the Tanimoto similarity of the generated compounds for the two models estimated for 100 samples.

Exhaustive sampling of the near-neighborhood

The correlation between the NLL and molecular similarity implies that sampling to a specific NLL threshold corresponds to exhaustively sampling of the near-neighborhood chemical space around a given source molecule. That is, given a source molecule of interest, the proposed training method for the transformer model creates a controlled and approximately complete enumeration of the local, precedented near-neighborhood chemical space for a given source molecule. The user can decide how large the chemical space should be sampled by varying the beam size. To demonstrate this results, we exhaustively sampled the near-neighborhood of all molecules in the TTD database with a large beam size of B = 30,000. All of the resulting generated target molecules with Tanimoto similarity greater or equal than 0.8 were extracted. We denote this set the near-neighborhood. Larger molecules have a larger near-neighborhood chemical space for a for a fixed Tanimoto similarity, and therefore source molecules were grouped based on their heavy atom count (HAC). Between ${\mathcal{O}}(10)$ and ${\mathcal{O}}(1{0}^{4})$ on average near-neighbors for source molecules between 13 and 36 heavy atoms, respectively (Fig. 2) were identified. A similarity threshold of 0.8 is chosen for illustrative purposes and represents a reasonable choice for a near-neighborhood chemical space. Supplementary Fig. 4 depicts the estimated near-neighborhood size for HAC 13-36 for different similarity thresholds for a beam size of B = 30,000. The transformer model based on count fingerprints trained with λ = 10 always generate larger near-neighborhoods than the model trained with λ = 0.

Fig. 2: Average neighborhood size (y-axis in log scale), defined by a similarity threshold of 0.8, to a source compound grouped by their number of heavy atoms (x-axis).

The Tanimoto similarity was evaluated with ECFP4 fingerprints with counts. The transformer models trained with λ = 10 always outperforms the transformer models trained with λ = 0. λ represents the hyperparameter controlling the regularization term. The filling color surrounding solid lines from HAC (heavy atom counts) 1 to 12 and 19 to 36 represent the standard deviation. The standard deviation is calculated based on a variable number of samples, which depends on the HAC and the specific dataset or generated compounds. Due to computational complexity, the similarity on GDB-12* was computed with ECFP4 fingerprints without counts. Also included in the figure is the size of the near-neighborhood retrieved from PubChem for each source compound. For HAC between 13 and 18, the neighborhood size was plotted explicitly since only a few source compounds were available in the TTD database, whereas for a HAC greater or equal than 19 the average and standard deviation are depicted.

To understand how close the results are to a truly exhaustive sampling of the local chemical space, we created the GDB-12 database, which was extracted from the GDB-13 database³¹. The GDB-12 database enumerates all possible compounds based on a set of rules up to 12 heavy atoms. The heavy atoms used are C, N, O, S, and Cl. This is, to our knowledge, the most complete lower bound of the possible density of organic chemical space available. For each compound in GDB-12, we computed the number of neighbors inside GDB-12 up to the same similarity threshold, and grouped them by the HAC.

We observed an exponential relationship between the HAC and the near-neighborhood size for GDB-12 (Fig. 2). Although the vocabulary set used for creating GDB-12 is smaller than the vocabulary set, V, used to train the transformer models, the behavior of trained transformer models follow the same trend as shown by GDB-12 for larger HAC, with an approximate linear slope of 0.10 and intercept of 0.55 for both GDB-12 and TTD for HAC 13-36 (i.e., neighborhood size ≈ 10^{0.10 HAC+0.55}). This suggests that, while our sampling remains a lower bound on the full local chemical space, it is approximately as complete as the enumerated near-neighborhood for the GDB-12 database. More approximations of the neighborhood size for different similarity thresholds can be found in Supplementary Fig. 5.

We also compared the results to the number of near-neighbors that could be retrieved by searching PubChem with the same similarity cutoff and source compounds. On average two orders of magnitude fewer near-neighbor compounds compared to the number of near-neighbors generated with the transformer models were retrieved. This highlights that the near-neighborhood, even for therapeutic molecules in the TTD database, is relatively unexplored.

Finally, we investigated the overlap between the generated similar target molecules with the transformer models and the similar molecules identified in PubChem with a given source molecule. This was done to assess if the trained transformer models identifies the same near-neighbors as was identified in Pubchem. As expected the trained transformer models are indeed able to retrieve most of the near-neighbors in PubChem with ~98% average recovery rate. As will be discussed in the section “Validation for novel compound series”, the missing near-neighbors not identified by the transformer models in Pubchem were missed because of two reasons. First, beam search is an approximation of an exhaustive search, meaning that there is no guarantee to find all the molecules below a certain NLL. Second, the transformer models do not provide a perfect correlation between the NLL and molecular similarity, meaning that the NLL between two similar source and target compounds can be high (low precedence) if the molecular transformation from the source molecule to the target molecule is not well represented in the training set. Incorporation of the ranking loss and count fingerprints both improve recovery, from 96.98% to 98.15% for models trained on ${\mathcal{D}}$ with λ = 0 and λ = 10, and from 97.19% to 98.38% for models trained on ${{\mathcal{D}}}^{c}$.

Validation for novel compound series

It is also of interest to validate the transformer model for retrieving similar compounds in a series of interest to a medicinal chemist. Therefore 200 chemical series from the recent literature were extracted from the ChEMBL database and collected in ChEMBL-series. The 200 series were used to evaluate if the trained transformer model can efficiently retrieve near-neighbors of interest. This was done through retrospectively investigating if known near-neighbors could be identified within the 200 chemical series. All the compounds within the 200 series are different from the training set for the transformer models, having been published after our training set was created. As an illustration, Fig. 3 depicts a chemical series in ChEMBL-series consisting of five compounds. Here, the series is represented as a graph where nodes are the compounds in the series and edges depict the NLL for the transformation of the source molecule to the target molecule and the Tanimoto similarity (calculated with ECFP4 count fingerprints) for the compound pairs. Note, that the Tanimoto similarity is symmetric for the molecular pair but the NLL is not, meaning that in general p(t∣s) ≠ p(s∣t), where s and t are the source molecule and target molecule, respectively. The transformer used in this experiment was trained with a regularization term and the ECFP4 count fingerprint. As expected, the NLL is strongly correlated with similarity and the NLL is lower for similar compounds and higher for dissimilar compounds. The difference between p(t∣s) and p(s∣t) is small when the compounds are similar. The lower-left plot in Fig. 3 shows the correlation between the molecular similarity and the NLL evaluated for all pairs in all of the 200 extracted chemical series. The correlation coefficient is 0.88, confirming the efficacy of the proposed ranking loss used in the training of the transformer. The similarity between compounds in the chemical series can be as low as 0.2, since the series assignment is solely based on that the compounds were extracted from the same publication. We observed markedly-poorer correlation between the NLL and the similarity for compound pairs with low similarity. The NLL decreases more rapidly for compound pairs with low similarity (deviations from the linear fit in Fig. 3). This is expected since our training of the transformer only includes source-target molecular transformations where the similarity is above ≥0.50, i.e., the model has not been trained on molecular transformations of pairs with a similarity below  <0.50 and accordingly these source-target molecular transformations have a low probability to be generated. The lower-right plot in Fig. 3 depicts the maximum NLL as a function of the beam size. Here, the NLL consistently increases as the beam size increases, allowing an exploration of an increasingly dissimilar chemical space.

Fig. 3: Overview of Tanimoto similarities (denoted with Sim in the figure) and NLLs (negative log-likelihoods) for a ChEMBL-series consisting of five compounds.

To the top the ChEMBL-series consisting of five compounds and displayed as a graph, where the nodes depict molecules and the edges depict the NLL of the molecular transformation and the Tanimoto Similarity (Sim in the plot) between the two connected nodes (molecules). Note that the NLL is not symmetric between a compound pair. The arrows on top of NLL denote the direction of the molecular transformation from the source molecule. If any generic pair of molecule in the graph s and t are connected then ${\overrightarrow{NLL}}$ denotes $-\log p(t| s)$ and ${\overleftarrow{NLL}}$ denotes $-\log p(s| t)$. The lower-left plot depicts the correlation between Tanimoto similarity (evaluated on fingerprints with counts) and the NLL for the molecular transformation for all the possible pairs contained in the 200 compound series. The red dots denote all the pairs of the above series. The lower-right plot illustrates the maximum NLL reachable with different beam sizes. The fill color surrounding the solid lines represents the standard deviation, which is calculated based on the beam the 200 compound series.

We repeated the analysis for all of the 200 compound series, for each series we considered in-turn all of the compounds as source molecules. Table 2 shows the results for beam sizes equal to 1000, 5000, and 10,000. To understand the results in Table 2 we need to introduce two cutoff thresholds, t_nll and t_sim, calculated for each series and each source compounds in the series. t_nll is defined as the highest NLL associated to a source compound found by beam search, while t_sim is defined as the similarity between the source compound and the target compound with the highest NLL found by the beam search. The choice of t_sim is reasonable as we report averaged results and therefore potential error would be canceled out, as confirmed by the low standard deviations reported in Table 2. We define as true positive (TP) the percentage of target molecules found by beam search, with true negative (TN) the percentage of target molecules not found by beam search where their similarity to the source molecule is lower than t_sim, and with false negative (FN) the percentage of remaining target molecules not found by beam search but should have been found in an ideal scenario. There are two types of FN: either due to beam search being an approximation of an exhaustive search, i.e., target compounds that have Tanimoto similarity greater than t_sim and NLL lower than t_nll (column FN-B in Table 2), or due to precedence i.e., target compounds that have a Tanimoto similarity greater than t_sim and NLL greater than t_nll (column FN-P in Table 2). In the latter case, the transformation between the source and target molecule is not well precedented in the training set and accordingly the NLL for the molecular transformation will be high. Table 2 reports mean and median, denoted with $\bar{x}$ and $\tilde{x}$, respectively, for TP, FN, and TN. The majority of the target compounds are retrieved correctly (TP + TN), while the FN are due to the limitations with beam search (slightly more) and low precedence (slightly less) for the transformation between the source and target molecule. We additionally calculated the rate of FN identified for beam size 1000 shifting to TP when the beam size increased from 1000 to 5000, having a decrease from 4.69% to 3.77% for FN due to the limitations of beam search, and an increase from 3.41% to 3.64% for FN due to low precedence of the molecular transformation. Thus it is possible through increasing the beam size to compensate for that the beam search is only an approximation of exhaustive search. We also computed the same metrics for a beam size of 10,000. A further decline in FN due to the limitations with beam search was observed to 3.48%. FN due to limited precedence of the molecular transformation decreased to 3.29% with 10,000 beam size. The percentages of FN in Table 2 for a beam size of 1000, 5000, and 10,000 show a decreasing trend with increased beam size. Thus it is shown that most near-neighbors to a compound in a compound series can be retrieved with a transformer regularized with a similarity constraint during training. The analysis of different physico-chemical properties also shows that the generated target molecules follow the same property distributions as the source molecules (see Supplementary Figs. 7 and 8).

Table 2 The table gives an overview of how well near-neighbors in a chemical series are retrieved with a transformer

Figure 4 highlights some limitations of the proposed method. A compound series with five compounds is used to illustrate the limitations. A compound was selected as source (the left-most in Fig. 4) and the remaining are the target compounds. Beam search with two different beam sizes, 1000 and 5000, was used and it was checked which of the target compounds was retrieved by the beam searches. The maximum NLL reachable by beam search was 11.90 and 12.63 for beam sizes of 1000, and 5000, respectively. This means that the compounds (represented to the right of the vertical red line in Fig. 4) for which the NLL is above these numbers cannot be retrieved as a larger beam size would be required. There are two reasons why a specific target compound is not found. The first is due to the beam search algorithm being a trade-off between a greedy and an exhaustive search controlled by the beam size. We notice that for beam size equals to 1000 the second compound in the series is not found even though its NLL is lower than 11.90. This happens because there is no guarantee that beam search will always find all the compounds below the maximum reachable NLL. The second reason is due to precedence as our method does not provide a perfect correlation between NLL and similarity. A high NLL i.e., low precedence can occur for similar molecules if the molecular transformation from the source molecule to the target molecule is not well represented in the training set. This might occur for instance for molecules containing unusual functional groups. Figure 4 shows that the right-most compounds has higher similarity than other two but its NLL is higher, meaning that has lower precedence. The low precedence for the right-most compound might be due to the azo substructure. Unfortunately, determining which tokens are responsible for an increased NLL in relation to a target compound is a complex task. This complexity arises from the fact that the NLL is influenced by both the source molecule and the generated target tokens. It is possible that the NLL is spread across all the target tokens, or alternatively, it may remain low until a specific point and then sharply drop with the introduction of the next token in the target compound. This is a general limitation of transformer-based architectures.

Fig. 4: A chemical series with a source molecule and the retrieved target molecules (with green borders) with beam search for two different beam sizes (BS).

The red vertical line represents the maximum NLL (negative log-likelihood) reachable by the two beam search sizes which is 11.90 and 12.63 for BS = 1000 and BS = 5000, respectively. The compounds to the right of the red vertical line cannot be found with these beam sizes due to the high NLL for the molecular transformation. The right-most compound has a similarity (denoted with Sim in the figure) of 0.71 to the source compound but low precedence as the NLL is equal to 17.23. The low precedence for the molecular transformation might be due to the azo group which is a relatively uncommon chemical substructure in the training set.

Generalization of the method

To demonstrate the generality of the proposed methodology, we have carried out a comprehensive series of additional experiments, encompassing:

• 1. eight experiments utilizing a dataset derived from ChEMBL. These experiments involve training two distinct models with two different similarity metrics, both with and without the incorporation of the proposed ranking loss;

• 2. an experiment with synthetic data (see Supplementary Section 2.1) which considers another similarity metric.

We used the dataset of pairs extracted from ChEMBL (direct link to the dataset: https://zenodo.org/records/6319821) by considering Tanimoto similarity greater or equal than 0.5 defined in ref. ²⁵. The dataset contains 6,543,684 training pairs, 418,180 validation pairs, and 475,070 test pairs. We also considered two similarity measures:

• k₁—Tanimoto similarity on ECFP4 with counts;

• k₂—Similarity induced by the autoencoder, as defined in ref. ³². In essence, the autoencoder takes a SMILES and employs a LSTM encoder network to generate a representation $z\in {{\mathbb{R}}}^{256}$ for the entire sequence. This representation can be utilized to compute a similarity measure between z_s and z_t, associated with a source s and target t, respectively, as follows:

  $${k}_{2}({z}_{s},\,{z}_{t})={z}_{s}^{T}{z}_{t},\quad {k}_{2}({z}_{s},\,{z}_{t})\in {\mathbb{R}}.$$

  (1)

The two similarities, k₁ and k₂, are poorly correlated (the Pearson correlation coefficient is equal to 0.27), and exhibit weak correlation and distinctions, as illustrated in Supplementary Fig. 9.

Regarding the models, we selected the identical transformer employed in the “Results” section and a straightforward sequence-to-sequence recurrent neural network (RNN) model, comprising a gated recurrent unit (GRU³³) encoder and decoder with 512 units each. Both models were trained with and without the ranking loss (refer to Eq. (3)), incorporating the two distinct similarity metrics, k₁ and k₂, for 30 epochs. We tested all the models by randomly selecting the same 1000 source compounds from the test set and running beam search with beam size B = 100. For all the generated compounds we reported the validity (see the section “Evaluation metrics”) and the correlation (see the section “Evaluation metrics”) between the chosen similarity. Table 3 shows the results demonstrating that the utilization of ranking loss consistently enhances the correlation between NLL and similarity (either k₁ or k₂ in this instance), independently of the specific model or dataset employed. Additionally, in conjunction with the experimental findings outlined in the “Results” section and Supplementary Section 2.1, we have provided a comprehensive overview, demonstrating the consistency of our framework across diverse datasets, models, and similarity metrics. The lower performances of the RNN compared to the Transformer are expected and attributed to its considerably smaller number of parameters, making it inherently more challenging to train. Nonetheless, it is important to highlight that the generated compounds exhibit a validity exceeding 70% across all cases, and the correlation consistently improves with the adoption of the ranking loss.

Table 3 VALIDITY and CORRELATION (see the section “Evaluation metrics” for definitions) for the RNN (recurrent neural network) and Transformer models, considering similarity k₁ and k₂ trained with and without ranking loss

Discussion

In this paper, we have introduced a strategy for training a source-target molecular transformer that explicitly links the NLL for molecular transformation of a source molecule to a target molecule with a similarity metric. The method has been applied in the context of molecular optimization. A transformer model has been trained on, to the best of our knowledge, the largest dataset of molecular pairs so far. The resulting model exhibits the intended relationship between the molecular similarity and the corresponding NLL, with a strong correlation across similarity ranges from 0.50 to 1.0 when evaluated for drug-like molecules, including molecules absent from the extensive training set. We could demonstrate a clear benefit in terms of the correlation between molecular similarity and NLL when applying our regularization method. The limitations of using a binary fingerprint vs a count fingerprint for the transformer model have also been described.

A model that exhibits this property can be used in novel applications for instance to estimate the density of the near-neighborhood chemical space. This was previously not possible. In particular, we could demonstrate an approximately exhaustive enumeration of the local, precedented chemical space for a molecule of interest. We showed that neighborhood sizes computed using this method scale in a similar way as the GDB-12 database.

From a drug design perspective, the presented model will be most influential at a later drug development stage, where the focus changes to exploring the chemical space around a lead compound. Using our model, we can cheaply but extensively explore the chemical space without being limited to available building blocks or previously synthesized molecules, and without needing to conduct similarity searches against massive virtual libraries. In a second step, a property evaluation of the generated molecules would follow to select the most promising compounds to follow up in a target-appropriate manner. Evaluation of such proprieties is target and project-dependent and not the focus of the current work. However, we emphasize that the models developed here can be practically useful idea generators for drug discovery applicable out of the box, and here we provide a simple example of using them for the structure-based virtual lead optimization of Phosphoinositide-dependent kinase-1 (PDK1) inhibitors in Supplementary Section 6.

We also investigated how many of the similar compounds we could retrieve in a chemical series extracted from the literature. With a beam search of 10,000, it was found that ~87% of the similar compounds could be retrieved. Reasons that a similar compound could not be retrieved is due to that beam search is an approximation of an exhaustive search or that the transformation from a source compound to a target compound have low precedence, i.e., the transformation is not well represented in the training set. This might happen for uncommon chemical substructures. Low precedence have been discussed in the context of modifying an atom in penicillin.

We believe that a molecular transformer model trained with a regularization term for the molecular similarity provides a completely novel way to address the classic question of how many near-neighbors a given molecule has. The transformer model therefore holds great promise as a tool for local molecular optimization and efficient local chemical search in a more exhaustive and controllable manner than previously possible. The proposed methodology to train transformer with a similarity metric as a regularizer is general and not dependent on any specific selected similarity metric. Here we have exemplified the methodology with binary and count versions of the ECFP4 fingerprint. However, any other similarity metric could have been used. If anyone is interested in another similarity metric, a transformer can be trained from scratch with that similarity metric. Alternatively, the trained transformer described here can be fine-tuned with molecular pairs constructed through another similarity metric.

Developed software, trained transformer models, and curated datasets will be publicly released upon acceptance of the manuscript.

Methods

Transformer model with a regularized loss function

A transformer^11,24,25 architecture trained on a SMILES (simplified molecular-input line-entry system) string representation of a molecule was used. The purpose of the study is to compare our proposed framework for training a molecular transformer with a regularized loss function with existing unconstrained training framework²⁵. However, our framework can in general be applied to any transformer model based on molecular pairs constructed with a similarity metric. Formally, we denote with ${\mathcal{X}}$ the chemical space, and with ${\mathcal{P}}=\{(s,t)\,| \,s,t\in {\mathcal{X}}\times {\mathcal{X}}\}$ the set of molecular pairs constructed from ${\mathcal{X}}$, s and t are the source and target molecules, respectively. Each element of sources and targets is a token (symbol) which takes values from a vocabulary (ordered set) V. Furthermore, we denote with ${f}_{\theta }:{\mathcal{X}}\times {\mathcal{X}}\to {[0,1]}^{| V| }$ the transformer with θ being the set of its parameters. To simplify, we denote with the same symbol a molecule and its SMILES string representation. The transformer, f_θ, consists of an encoder and a decoder which are simultaneously fed by source molecules and target molecules, respectively. Source molecules and target molecules are first tokenized and then converted into sequences of dense vector embeddings and passed over several stacked encoder and decoder layers, respectively. The final encoder output is merged into the decoder through a multi-head attention mechanism which captures the transformation from a source molecule to a target molecule. Figure 5 shows the general architecture of our transformer model, more details about the transformer architecture can be found in refs. ^11,24,25.

Fig. 5: Transformer training and inference flows are shown.

The training is depicted to left (a), while the inference to the right (b). a The transformer model receives as input pairs of molecules consisting of a source molecule and a target molecule (represented as SMILES strings). The SMILES associated to source and targets are CC(Cc1ccc(Cl)cc1)NCC(O)C(N)=O and CC(Cc1ccc(O)cc1)NCC(O)C(N)=O, respectively. The initial character of the target SMILES provided as input is the starting token ˆ. The model is trained to transform a source molecule to a target molecule by producing its next tokens (in parallel). The last character of the produced output is the ending token $. At training molecular pairs of source and target molecules are used to train the transformer model. b At inference a source molecule is transformed into several target molecules. In the figure, those are sampled target₁ and sampled target₂ corresponding to SMILES CC(Cc1ccc(Cl)cc1)NCC(O)C(N)=S and CC(Cc1ccc(Cl)cc1)NCC(F)C(N)=O, respectively.

f_θ models the probability p of the ℓ-th token of a target t_iℓ given all the previous t_i,1:ℓ−1 = t_iℓ−1, …, t_i1 target tokens and source s_i compound, i.e., f_θ(t_i,1:ℓ−1, s_i)[t_iℓ] = p(t_iℓ∣t_i,1:ℓ−1, s_i). The transformer’s parameters θ are then trained on ${\mathcal{P}}$ by minimizing the negative log-likelihood (NLL) of the entire SMILES string, p(t_i∣s_i), $({s}_{i},{t}_{i})\in {\mathcal{P}}$ for all $i=1,\ldots,| {\mathcal{P}}|$, that is

$${\text{NLL}}_{i}= -\log p({t}_{i}| {s}_{i})=-\log \mathop{\prod }\limits_{\ell=1}^{L}p({t}_{i\ell }| {t}_{i\ell -1},\ldots,{t}_{i1},\,{s}_{i})\\= -\mathop{\sum }\limits_{\ell=1}^{L}\log p({t}_{i\ell }| {t}_{i\ell -1},\ldots,{t}_{i1},{s}_{i})=-\mathop{\sum }\limits_{\ell=1}^{L}\log {f}_{\theta }({t}_{i,1:\ell -1},\,{s}_{i})[{t}_{i\ell }],$$

(2)

where L denotes the number of tokens associated to t_i, and [t_iℓ] denotes the index of vector f_θ(t_i,1:ℓ−1, s_i) corresponding to the token t_iℓ. The NLL represents the probability (precedence) of transforming a given source molecule into a specific target molecule. The NLL is always non-negative and the higher the NLL value, the less likely a target molecule will be generated. A NLL equal to 0.0 would imply that a specific target molecule would have the probability of 1.0 to be generated from the source molecule.

The loss in Eq. (2) allows the transformer to learn but it associates equal probabilities (i.e., same negative log-likelihood) to all the target compounds associated to the same source molecule. This uniform assignment occurs because the model observes these target compounds an equal number of times. This behavior is not ideal since during inference we would like the probability of generating a target molecule given a specific source molecule, p(t∣s), to be proportional to the similarity between the molecules. To mitigate this issue, we introduce in Eq. (3), a regularization term to the loss in Eq. (2) which penalizes the NLL if the order relative to a similarity metric is not respected.

$$\Omega (({s}_{i},\,{t}_{i}),\,({s}_{j},{t}_{j}))=\max (0,\,{\rm{sign}}\,(\kappa ({s}_{i},\,{t}_{i})-\kappa ({s}_{j},\,{t}_{j}))\,({\rm{NLL}}_{i}-{\rm{NLL}}_{j})),$$

(3)

where (s_i, t_i) and (s_j, t_j) are two pairs from ${\mathcal{P}}$, and κ is an arbitrary kernel function. The Tanimoto similarity was chosen as κ but our framework is general so any valid kernel can be used. Note that the NLL is always non-negative in this context. During training, we sample a batch of source-target molecule pairs and compute the regularization term in Eq. (3) for all the molecular pairs included in the batch. Figure 6 depicts an example of the ranking loss calculation. Finally, to train the model we propose the following loss function as a combination of Eqs. (2) and (3)

$${\mathcal{L}}=\frac{1}{| {\mathcal{P}}| }\mathop{\sum }\limits_{i=1}^{| {\mathcal{P}}| }{\text{NLL}}_{i}+\frac{\lambda }{| {\mathcal{P}}| (| {\mathcal{P}}| -1)}\mathop{\sum }\limits_{i=1}^{| {\mathcal{P}}| -1}\mathop{\sum }\limits_{j=i+1}^{| {\mathcal{P}}| }\Omega (({s}_{i},\,{t}_{i}),({s}_{j},\,{t}_{j})),$$

(4)

where λ ≥ 0 is a hyper-parameter controlling the weight of the regularization term.

The molecular similarity is in this study related to the notion of precedence. Precedence is learnt by a transformer model based on the training data and represents the probability for a source compound to be transformed into a specific target compound. The NLL can be used as proxy for the precedence where a low NLL means a high precedence and vice versa. Figure 7 illustrates an example where a nitrogen atom in penicillin is replaced by a oxygen atom, phosphorus atom, or arsenic atom, respectively. It is important to notice that the Tanimoto similarities (calculated with the count version of ECFP4 fingerprints) between Penicillin and the modified penicillin analogs are exactly the same, while their NLLs are different, as the penicillin analog with an arsenic atom has lower precedence than the penicillin analog with a phosphorus atom, and the penicillin analog with a phosphorus atom has lower precedence than the penicillin analog with an oxygen atom and the penicillin analog with an oxygen has lower precedence than penicillin itself. We can therefore expect that the penicillin analog with an oxygen atom will be retrieved with a much higher precedence (probability) during inference than the penicillin analogs with a phosphorous atom or arsenic atom, respectively.

Fig. 6: Two pairs of molecules (s₁, t₁), (s₂, t₂) with Tanimoto similarity 0.71 and 0.76, respectively, are shown.

The Tanimoto similarity is represented by κ in the Figure, and s₁ and s₂ denote two source molecules, while t₁ and t₂ two targets molecules. NLL₁ and NLL₂ are the negative log-likelihood associated with (s₁, t₁) and (s₂, t₂), respectively. In the left example NLL₂ > NLL₁, therefore the regularization term Ω (see Eq. (3)) is greater than 0. This indicates that NLL₁ and NLL₂ are incorrectly ordered, which we emphasize by enclosing Ω = 1.8 in a red box in the left picture. In the right example NLL₁ > NLL₂. In this case, Ω = 0 as the similarities and NLLs have the same rank-order, which we emphasize by enclosing Ω = 0.0 in a green box in the right picture.

The implementation relies on Python 3.9 with the following libraries: cupy-cuda11 10.6.0, lightning 2.0.1, MolVS 0.1.1, natsort 7.1.1, numpy 1.24.4, pyyaml 6.0.1, rdkit 2022.9.7, scipy 1.10.1, torch 1.12.1, and tqdm 4.65.0. The datasets used in the paper are available at https://doi.org/10.5281/zenodo.12818281. Source data are provided with this paper.

Fig. 7: Penicillin (used here as the source molecule) and its analogs where a nitrogen atom (N) is replaced with an oxygen atom (O), phosphorus atom (P), and arsenic atom (As), respectively.

The area enclosed within the orange circles in the lower part of the figure contains the atoms that differ from the penicillin. The molecular similarity, denoted with S in the figure, between Penicillin and the modified analogs are the same, while their corresponding NLLs (negative log-likelihoods or precedence) are different. The molecular transformation from penicillin to the analog with an arsenic atom has lower precedence (higher NLL) than transforming penicillin to the analog with phosphorus and oxygen, respectively. The derivative with an oxygen atom has the highest precedence after penicillin. The Tanimoto similarity is denoted with the letter S on top of the penicillin analogs in the lower part of the figure.

Approximately exhaustive sampling of the chemical space

Two different techniques can be used to sample target molecules with a molecular transformer: multinomial sampling (used e.g., by He et al.^24,25) and beam search³⁴. Multinomial sampling allows fast generation of compounds distributed according to their NLL. Given a source compound $s\in {\mathcal{X}}$, the length L of the tokens in the SMILES string associated with s, and V the vocabulary, i.e., the set of possible tokens, the computationally complexity of multinomial sampling is O(L ⋅ ∣V∣). However, multinomial sampling suffers from mode collapse i.e., the same target compound might be sampled multiple times, and the method is not deterministic, i.e., different runs produce different target compounds. Beam search is, in contrast to multinomial sampling, deterministic but computationally more complex ${\mathcal{O}}(B\cdot L\cdot | V| )$, where B is the beam size. Beam search retains B unique SMILES strings sorted by their corresponding NLL. Note that for both the techniques, the complexity of the underlying transformer model impacts the performance. This complexity arises because SMILES strings are generated iteratively by feeding the transformer with n − 1 tokens to obtain the n-th. In fact, for multinomial sampling, the model needs to compute the probabilities of each token in the vocabulary, while for beam search, we need to store the B SMILES subsequences with the most favorable NLL. Similarly to multinomial sampling, we also need to compute the probabilities of each token in the vocabulary for each subsequence. Note that beam search is an approximate exhaustive search and it might miss compounds with a favorable NLL.

Data preparation

Molecular structures were downloaded from PubChem as SMILES strings. In total 102,419,980 compounds were downloaded (PubChem dynamically grows. This number reflects the available compounds by the end of December 2021). The dataset was pre-processed as follows:

• the SMILES strings were standardized using MolVS (https://molvs.readthedocs.io/en/latest) including the following steps: sanitize, remove hydrogens, apply normalization rules, re-ionize acids, and keep stereo chemistry;

• all duplicate structures were removed;

• all the compounds containing an isotopic label were removed.

Starting from the set of pre-processed SMILES strings ${\mathcal{X}}$ (containing 102,377,734 SMILES strings), we constructed a dataset ${\mathcal{D}}=\{(s,t)\,| \,s,t\in {\mathcal{P}},\,\kappa (s,t)\ge 0.5\}$ containing all the pairs having a Tanimoto similarity κ(s, t) ≥ 0.50. The Tanimoto similarity is calculated with the RDKit³⁵ (version 2022.09.5) Morgan binary fingerprint (ECFP4) with radius equals to 2, 1024 bits, calculated from the SMILES strings in ${\mathcal{X}}$. The number of molecular pairs in ${\mathcal{D}}$ is 217,111,386,586, which is only 0.002% of the over 10¹⁶ possible molecular pairs). The Tanimoto similarity for the molecular pairs can be computed efficiently by storing the fingerprints in a binary matrix of size N × 128 bytes in the GPU memory. In this way, the Tanimoto similarity among all the possible pairs can be efficiently computed by utilizing GPU parallelism. For each SMILES string in ${\mathcal{X}}$ we can calculate the Tanimoto similarity at once against all the other SMILES strings. The calculation of all molecular pairs took 10 days on 16 A100 GPUs with 40GB of memory.

Starting from ${\mathcal{D}}$, we constructed an additional dataset ${{\mathcal{D}}}^{c}$ where we kept all the pairs having a ECFP4 Tanimoto similarity with counts greater or equal than 0.50. The major advantage of Morgan fingerprints with counts compared to their binary counterpart is their ability to capture the frequency of a substructure within a molecule. Using count fingerprints makes it possible to differentiate between molecules having the same substructures but different frequency of them and therefore a lower similarity value can be assigned when comparing the two molecules. Supplementary Fig. 2 shows an example of the Tanimoto similarity between two molecules with the binary and count fingerprints. The Tanimoto similarity with count fingerprints cannot be computed as efficiently as for binary fingerprints, therefore we first construct ${\mathcal{D}}$ and then refine it to obtain ${{\mathcal{D}}}^{c}$, where for each pair ${\mathcal{D}}$ we recomputed the Tanimoto similarity on fingerprints with count and kept only those with values greater or equal than 0.50. ${{\mathcal{D}}}^{c}$ contains 173,911,600,788 pairs. In the “Results” section, we will show results for both ${\mathcal{D}}$ and ${{\mathcal{D}}}^{c}$.

Transformers receive a sequence of integers, therefore each SMILES string is first tokenized and then translated into a specific integer number. The tokens are collected into a dictionary where keys are tokens and values are integers, that is

$$V=\left\{*: 0,\!\! \hat {\;\;\;\;:\;} 1,\, \$ : 2, < {\rm{UNK}} > : 3,\ldots,\, 1 : 48,\ldots,\, {\rm{C}} : 60,\, {\rm{Cl}} : 61,\ldots \right\}.$$

Note that V contains 4 special tokens: * is the padding token used to enforce the same length of all SMILES, ˆ is the starting token, $ the ending token, and <UNK> is the unknown token used at inference time if a new token is observed. We constructed V from ${\mathcal{D}}$ which contains 455 different tokens. Supplementary Fig. 1 shows an example of the SMILES string tokenization procedure.

Model training and sampling

Four transformer models were trained on ${\mathcal{D}}$ and ${{\mathcal{D}}}^{c}$ and with and without ranking loss. In our experiments, we employed a standard transformer model^11,25 with the following key parameters:

• Number of layers:

  • — Encoder layers: the model consists of N = 6 identical layers in the encoder stack. Each encoder layer consists of two main sub-layers: a multi-head self-attention mechanism and a position-wise fully connected feed-forward network.

  • — Decoder layers: Similarly, the decoder stack also contains N = 6 identical layers. Each decoder layer includes an additional sub-layer for multi-head attention over the encoder’s output.

• Hidden dimension: the dimensionality of the input and output vectors, denoted as d_model was set to 256. This dimension is consistent across all layers and serves as the size of the embeddings and the internal representations within the model.

• Feed-forward network dimension: within each layer, the position-wise feed-forward networks expand the dimensionality to d_f f = 2048. This expansion is achieved through two linear transformations with a ReLU activation in between.

• Number of attention heads: each multi-head attention mechanism is composed of h = 8 attention heads. The model splits the d_model = 256 into 8 subspaces of size 16. These heads allow the model to focus on different parts of the input sequence simultaneously.

• Dropout rate: to mitigate overfitting, a dropout rate of 0.1 was applied to the output of each sub-layer before adding the residual connection and layer normalization.

Every model was trained for 30 epochs, utilizing 8 A100 GPUs, with each training cycle lasting for 30 days. During an epoch all the source-target molecular pairs in the training set are included once. All models were trained following the same strategy and using the same hyperparameters as in ref. ²⁵, including a batch size of 128, Adam optimizer and the original learning rate schedule¹¹ with 4000 warmup steps. Due to the computational time required to train a model, we could not optimize λ (see the “Transformer model with a regularized loss function” section). However, while not necessarily optimal, the value we chose for λ, i.e., λ = 10 already highlights (see the “Results” section) the benefits from using the ranking loss when assessing the overall quality of the models.

Once trained, the models can be used to generate target molecules conditioned on a source molecule by predicting one token at a time. Initially, the decoder processes the start token along with the encoder outputs to sample the next token from the probability distribution over all the tokens in the vocabulary. The generation process iteratively continues by producing the next token from the encoder outputs and all the previous generated tokens until the end token is found or a predefined maximum sequence length (128) is reached. To allow for the sampling of multiple target molecules, beam search is used (see the “Approximately exhaustive sampling of the chemical space” section), and unless otherwise stated, a beam size of 1000 was used.

Evaluation setup

The model was evaluated on two publicly available datasets: the Therapeutic Target Database (TTD)³⁶ and ChEMBL-series which consists of compound series from recent scientific publications extracted from the ChEMBL database²⁷. TTD contains clinically investigated drug candidates, which we used to investigate exhaustive sampling of the near-neighborhood for drug-like molecules. The compound series from publications contains only novel molecules that were not part of our training data, resulting in a out-of-distribution set of molecules that we cluster into chemical series based on the publication that they were extracted from.

Each dataset was pre-processed using the strategy described in the “Model training and sampling” section, and compounds that contained tokens not present in the vocabulary V (used to train the models) were removed. A final filtering was applied to both datasets in order to remove peptides and other non-drug-like small molecules. Only compounds that satisfied all the following criteria were kept:

• Lipinski rule of five compliant³⁷;

• molecular weight larger than 300 Dalton;

• less than eight ring systems.

The final TTD dataset contains 821 compounds, while the ChEMBL-series dataset contains 2685 compounds distributed in 200 series with 5 to 60 compounds in each series. Both curated datasets are released together with the code. Notably, compounds from ChEMBL-series were selected to be distinct from both training sets ${\mathcal{D}}$ and ${{\mathcal{D}}}^{c}$, ensuring no overlap in between the sets.

Evaluation metrics

To evaluate the impact of ranking loss (see Eq. (3)) on a fully trained model we considered several metrics (for all of them the higher the better):

• VALIDITY: the percentage of target compounds generated by the transformer model that are valid according to RDKit. VALIDITY is calculated by averaging the percentage of valid target compounds sampled for each source compound;

• UNIQUENESS: the percentage of unique target compounds generated by the transformer model. In order to evaluate the uniqueness, the generated valid target compounds are canonicalized with RDKit to identify duplicates; UNIQUENESS is calculated by averaging the percentage of valid unique target compounds sampled for each source compound;

• TOP IDENTICAL: the number of cases where the target compound with the lowest NLL is identical to the source compound. TOP IDENTICAL allows to evaluate whether the ranking loss forces the transformer model to generate the source compound as the generated target compound with the lowest NLL. Note that, κ(s, s) = 1 for all possible source compounds s. TOP IDENTICAL is calculated by averaging over the source compounds;

• RANK SCORE: the Kendall’s tau score τ between the Tanimoto similarity and the NLL for the top ten compounds sampled by beam search. The score measures the correspondence between the two rankings. The score have values in [−1, 1] range, where the extremes denote perfect disagreement and agreement, respectively. Given a source compound s and N generated compounds ${\hat{t}}_{1},\ldots,{\hat{t}}_{N}$ from s, τ is computed as:

  $$\tau=\frac{2}{N(N-1)}\sum _{i < j}\,{\rm{sign}}\,(\log p({\hat{t}}_{j}| s)-\log p({\hat{t}}_{i}| s))\,\,{\rm{sign}}\,(\kappa (s,{\hat{t}}_{j})-\kappa (s,{\hat{t}}_{i})).$$

  (5)

• CORRELATION: the Pearson correlation coefficient between the Tanimoto similarity and the NLL, which measures the linear correlation between the Tanimoto Similarity and the NLL. It have values in the [ − 1, 1] range, where the extremes denote perfect disagreement and agreement, respectively. Given a set of pairs $P={\{({x}_{i},\,{y}_{i})\,| \,{x}_{i}\in {\mathbb{R}},\,{y}_{i}\in {\mathbb{R}}\}}_{i=1}^{N}$ the Pearson correlation coefficient is computed as:

  $$\rho=\frac{\mathop{\sum }\nolimits_{i=1}^{N}({x}_{i}-\bar{x})({y}_{i}-\bar{y})}{\sqrt{\mathop{\sum }\nolimits_{i=1}^{N}{({x}_{i}-\bar{x})}^{2}}\sqrt{\mathop{\sum }\nolimits_{i=1}^{N}{({y}_{i}-\bar{y})}^{2}}},$$

  (6)

  where $\bar{x}$ (and similarly $\bar{y}$) is the average of all the x_i, i.e., $\bar{x}=1/N\mathop{\sum }\nolimits_{i=1}^{N}{x}_{i}$. CORRELATION is calculated by averaging over all the sampled target compounds.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.