An end-to-end framework for the prediction of protein structure and fitness from single sequence

Abstract

Significant research progress has been made in the field of protein structure and fitness prediction. Particularly, single-sequence-based structure prediction methods like ESMFold and OmegaFold achieve a balance between inference speed and prediction accuracy, showing promise for many downstream prediction tasks. Here, we propose SPIRED, a single-sequence-based structure prediction model that exhibits comparable performance to the state-of-the-art methods but with approximately 5-fold acceleration in inference and at least one order of magnitude reduction in training consumption. By integrating SPIRED with downstream neural networks, we compose an end-to-end framework named SPIRED-Fitness for the rapid prediction of both protein structure and fitness from single sequence with satisfactory accuracy. Moreover, SPIRED-Stab, the derivative of SPIRED-Fitness, achieves state-of-the-art performance in predicting the mutational effects on protein stability.

Introduction

Proteins serve as the primary executors for biological functions typically by folding into unique three-dimensional structures, which highlights the importance of protein structure determination. The structural information of a protein is theoretically prescribed by its amino acid sequence¹, but could be excavated from the evolution of protein sequences more easily in practice^2,3,4,5,6. In the past years, deep learning models developed based on this principle have made remarkable progress in the field of protein structure prediction. Representative models, such as AlphaFold^7,8 and RoseTTAFold^9,10, utilize evolutionary information extracted from multiple sequence alignments (MSA) to predict protein structures and attain accuracy close to experimental results. Later on, single-sequence-based predictors, such as ESMFold¹¹, OmegaFold¹², HelixFold-Single¹³, trRosettaX-Single¹⁴, and RGN2¹⁵, have been designed to accelerate protein structure prediction by employing the pre-trained protein language model (PLM), which learns evolutionary information hidden in the dependencies between amino acids from hundreds of millions of available protein sequences. As an example, ESMFold and OmegaFold can accomplish the structure prediction for generic proteins in the time scale of seconds, surpassing the speed of AlphaFold by orders of magnitude. Despite the amazing progress, current structure prediction methods still have limitations, mainly in the prohibitive computational cost in both inference and model training. Firstly, in situations with a limited number of GPUs, which is typical for ordinary research groups, both ESMFold and OmegaFold are still speed-inadequate for high-throughput structure prediction. For instance, it takes around 8 s to predict the structure of a 500-residue protein using ESMFold and OmegaFold (without recycling). If applied for tens of thousands or millions of mutant sequences, the aforementioned methods will be time-consuming for the generation of structural features required by downstream protein functional analysis and prediction tasks. Secondly and more importantly, whether it is AlphaFold or ESMFold, the training procedure requires significant computational resources that far exceed the affordability of ordinary research groups. This hinders the extensive explorations on the modification of model architecture, the update of model parameters by retraining, as well as the finetuning of structure prediction models for downstream functional analysis.

Considering the decisive impact of protein structures on their functions, one of the ultimate goals of protein structure determination or prediction should be to facilitate the engineering of protein functions through sequence modification^16,17. In the rational design or engineering, the protein sequence could be changed to alter the protein structure or structural stability, eventually achieving protein functional remodeling. Historically, intensive labors and resources have been invested to screen a large number of mutants for proteins with various desired functions (e.g., the enzyme activity and protein stability), which are comprehensively named as the protein fitness¹⁸. Obviously, accurate prediction of the fitness changes caused by single and multiple mutations is of high importance in protein design and functional studies. Numerous previous researches suggest that proper utilization of protein structural information could effectively enhance the accuracy of protein fitness prediction^19,20,21. With the rapid development in the field of protein structure prediction, vast structures predicted by AlphaFold and ESMFold allow the overcoming of previous challenges caused by the limited number of experimentally resolved protein structures^22,23,24. In a recent work, we proposed a method called GeoFitness²⁵, which significantly improves the prediction of mutational effects on protein fitness as well as two specific downstream metrics of protein stability, namely the ΔΔG and ΔT_m, by utilizing input features extracted from AlphaFold-predicted structures. Despite the success, such methods are still limited by the lack of communication between the sequence-based structural prediction and the structure-based functional prediction tasks, because results of the former are simply used as input features of the latter. Ideally, the structural prediction algorithm should be integrated as a part of the overall fitness prediction model, which not only enables sufficient communication between the structural prediction module and the fitness prediction module in the whole neural network through end-to-end model training, but also allows comprehensive utilization of existing data of protein sequences, structures and fitness scores to improve the prediction of protein mutational effects. Unfortunately, the heavy computational consumption of models like AlphaFold and ESMFold prohibits such an implementation. In this respect, a light-weight, fast protein structure prediction model with comparable performance to the state-of-the-art methods is still in urgent demand.

To address the limitations mentioned above, in this work, we first developed a protein structure prediction model, structural prediction based on inter-residue relative displacement (SPIRED), aiming for reducing the computational consumption. Through a distinctive design in model architecture and loss function, SPIRED achieves approximately 5-fold acceleration in the inference speed and at least 10-fold reduction in the training cost. Furthermore, SPIRED reaches comparable accuracy to the state-of-the-art methods like OmegaFold on CAMEO^26,27 and CASP15²⁸ benchmarks. Subsequently, by combining SPIRED and downstream graph neural networks, we proposed an end-to-end framework called SPIRED-Fitness, which is capable of rapidly and accurately predicting the protein structure and the fitness changes caused by all single and double mutations from the amino acid sequence simultaneously. Moreover, through end-to-end model finetuning, we demonstrated the feasibility of co-training the protein structural prediction module and fitness prediction module within a universal neural network and validated the assistance of this design in the further improvement of the protein functional prediction. Particularly, when reutilizing the pre-trained SPIRED-Fitness for the prediction of downstream metrics of ΔΔG and ΔT_m caused by mutations, the corresponding program SPIRED-Stab attains the state-of-the-art performance.

Results

Overview of algorithms

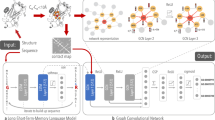
In this work, we propose an algorithm SPIRED to predict the structure from the amino acid sequence of a protein. SPIRED adopts an innovative model design of sequentially arranged Folding Units (Fig. 1a, b and Supplementary Fig. S1) and engages a relative displacement loss (RD Loss, Fig. 1c) to significantly improve the computational efficiency. After sufficient training using the PDB²⁹ database, SPIRED achieves comparable prediction accuracy to the other state-of-the-art methods, but with remarkably enhanced inference speed and significantly reduced training cost. The pre-trained SPIRED is then utilized as the information extractor in the SPIRED-Fitness model to predict the single and double mutational effects on the protein fitness from the wild-type amino acid sequence (Fig. 1d). SPIRED-Fitness is sufficiently optimized using a plethora of multi-labeled deep mutational scanning (DMS)³⁰ data. Subsequently, majority of the pre-trained SPIRED-Fitness model is reutilized in the SPIRED-Stab model to predict the change of protein stability, namely ΔΔG and ΔT_m, caused by an arbitrary number of mutations given the input of wild-type and mutant sequences (Fig. 1e).

Fig. 1: The model architecture of SPIRED, SPIRED-Fitness, and SPIRED-Stab.

a The model architecture of SPIRED and the protein structure prediction procedure by SPIRED and GDFold2³¹. b Diagram for information flows in the Folding Unit. Each Folding Unit can predict multiple sets of C_α coordinates. I/R/CN means Instance/Row/Column Normalization⁶⁰. c Comparison between the RD Loss and the FAPE Loss⁷. T_k in the FAPE Loss refers to the rotation matrix for the local coordinate system of residue k. In the RD Loss, the relative displacement between a pair of residues i and j is evaluated over all local reference frames, exemplified by k and l in the figure. N is the number of amino acid residues in the protein. d Prediction of protein fitness upon single and double mutations by SPIRED-Fitness using the wild-type sequence as input. e SPIRED-Stab combines the wild-type sequence and mutant sequence to predict protein stability changes caused by arbitrary mutations, with antisymmetry guaranteed. For both mutant and wild-type sequences, the model parameters within the gray box have shared weights. The SPIRED-Stab model parameters within the dashed box are initialized based on the final parameters of the SPIRED-Fitness model within the dashed box in subplot d.

SPIRED performs well for CAMEO and CASP15 targets without recycling

To validate the performance of our protein structure prediction method, we evaluate SPIRED against two state-of-the-art models, ESMfold and OmegaFold, on CAMEO and CASP15 targets at two options: Cycle = 1 (i.e. without recycling) and Cycle = 4 (i.e. four recycling cycles). Here, GDFold2³¹ is used to perform side-chain packing and main-chain adjustment for the C_α-based structures predicted by SPIRED (SPIRED+GDFold2 in Fig. 2). The CAMEO set has 680 single-chain proteins (released from August 2022 to August 2023). The CASP15 set contains 45 publicly released protein domains. Proteins in these test sets are all released after the date cutoff (March 2022) of the training set of SPIRED.

Fig. 2: Comparison of model performance on CAMEO and CASP15 targets.

a The boxplot compares the TM-scores of structures predicted by SPIRED, SPIRED+GDFold2, OmegaFold, and ESMFold with Cycle = 1 on the CAMEO set, which is composed of 680 samples of proteins. Here, the green triangle indicates the mean value with the corresponding number marked aside, the center line represents the median, the box limits correspond to the upper and lower quartiles and the whiskers extend to 1.5 inter-quartile range. A more detailed comparison is shown in the scatter plot, where each point represents a protein sample, the vertical axis represents the TM-score of SPIRED+GDFold2 predictions, and the horizontal axis represents the results of OmegaFold and ESMFold, respectively. b Similarly, the boxplot and scatter plot present the general and detailed comparisons between the evaluation results for these models with Cycle = 1 on the CASP15 set, which is composed of 45 samples of protein domains, whose sequences and ground truth structures are available from the CASP15 official website. The boxplot is constructed in the same way as that in subplot a. In both boxplots, the single-sequence-based predictors under evaluation are also compared with the standard AlphaFold2 (ColabFold⁶⁷ version, Cycle = 1) taking the MSA or single sequence as input, respectively, as well as an ultrafast predictor EMBER3D⁶⁸ (unrelaxed version). Source data are provided as a Source Data file.

Without recycling (Cycle = 1), SPIRED performs well on the CAMEO set (average TM-score³² = 0.786), slightly surpassing OmegaFold (average TM-score = 0.778), as shown in Fig. 2a. Notably, for the SPIRED prediction, GDFold2 optimization introduces a significant enhancement in the local structural quality despite a minor drop in the TM-score (see Supplementary Information 1.7 and Supplementary Table S1 for a detailed discussion). When four recycling cycles are employed (Cycle = 4), SPIRED exhibits a slightly lower prediction accuracy compared to OmegaFold: TM-score of 0.787 vs. 0.805 (Supplementary Fig. S2a). As for the CASP15 targets, SPIRED exhibits a similar prediction accuracy to OmegaFold at both options (Fig. 2b for Cycle = 1 and Supplementary Fig. S2b for Cycle = 4). Clearly, ESMFold shows better performances than SPIRED and OmegaFold on both CAMEO and CASP15 sets. This is, however, not unexpected considering that the model parameters of ESMFold outnumber those of SPIRED and OmegaFold by approximately five times, and that ESMFold engages a large amount of AlphaFold2-predicted protein structures for model training (Supplementary Table S11), both factors reported as essential for achieving the high prediction accuracy in the ESMFold paper¹¹. Incidentally, single-sequence-based protein structure prediction methods in general still can not reach the level of the MSA-based version of AlphaFold2 but outperforms the AlphaFold2 version that takes the single sequence as input.

Nevertheless, SPIRED exhibits considerable prediction accuracy in the absence of recycling, with a generally comparable performance to the nowadays state-of-the-art single-sequence-based protein structure predictors, which supports its candidate role for end-to-end training with downstream protein function prediction networks. Other models like OmegaFold rely on recycling to improve prediction accuracy, and the termination of gradients during recycling obviously hinders the joint training of such models with downstream networks in the recycling state. ESMFold, despite its high prediction accuracy without recycling, has vast model parameters and consumes large amounts of training GPU memory, thus exceeding the affordability of ordinary research groups for the similar joint training.

Evaluation of structure prediction at the level of protein folds

In previous studies, the performance evaluation of structure prediction models often focused on dozens or hundreds of proteins from double-blind competitions, which covered a limited range of topological structure types and therefore could not comprehensively evaluate the model performance on the protein folds of common interests. For instance, the 680 CAMEO proteins only cover 20.6% (253 out of 1,231) of the SCOPe³³ fold types based on Foldseek³⁴ search. Therefore, in this study, we systematically analyze the model performance at the level of all known protein folds (or topologies). The SCOPe³³ database categorizes experimentally determined protein structures into different folds, each containing one or more structural domains. We use SPIRED, ESMFold, and OmegaFold to predict the structures for 34,021 SCOPe domains belonging to a total of 1231 folds (in the SCOPe v2.08 S95 database), and take the average TM-score of all domains within each fold as the indicator of the model performance for this specific type of topology.

In general, SPIRED exhibits significantly better performance than OmegaFold and ESMFold on numerous folds (Fig. 3a, b). Particularly, SPIRED shows an advantage of > 0.2 in TM-score over ESMFold in 91 folds, whereas ESMFold outperforms SPIRED by >0.2 in TM-score only in 14 folds. The kernel density estimate (KDE) plot of TM-scores across different folds (Fig. 3c) clearly suggests that SPIRED has the lowest density in the low prediction accuracy region (i.e. 0.2 < TM-score < 0.5) and the highest density in the high accuracy region (i.e. TM-score = ~0.9) among the tested models. Detailed evaluations within the SCOPe classes show the similar trend (see Supplementary Figs. S3 and S4). Furthermore, SPIRED has a higher average TM-score over all folds than both OmegaFold and ESMFold (Fig. 3d). Taking the GFP protein folding type (SCOPe Fold ID: d.22) as an example, SPIRED has an average TM-score of 0.959, while OmegaFold and ESMFold can only achieve average TM-scores of 0.577 and 0.485, respectively. More case studies of successful SPIRED predictions could be found in Supplementary Fig. S5, while the SCOPe fold types poorly predicted (TM-score < 0.5) by SPIRED, OmegaFold and ESMFold are listed in Supplementary Data 1–3, respectively.

Fig. 3: Comparison of the prediction accuracy on the SCOPe v2.08 S95 structural classification database.

a, b In the scatter plot, each point represents the average TM-score of all domains of one fold in SCOPe. The vertical axis is the prediction performance (TM-score) of SPIRED on different SCOPe folds, while the horizontal axis represents results for OmegaFold and ESMFold, respectively. c The KDE plot is used to visualize the distribution of model performance (in TM-score) over different SCOPe folds for the tested models. d The boxplot compares the TM-scores calculated over all SCOPe folds (sample size = 1231) for different models, where the green triangle indicates the mean value with the corresponding number marked aside, the center line represents the median, the box limits correspond to the upper and lower quartiles and the whiskers extend to 1.5 inter-quartile range. Source data are provided as a Source Data file.

The same phenomenon is observed when evaluated at the level of CATH³⁵ topologies (Supplementary Fig. S6, see Supplementary Information 1.5 for details). Our analysis on the SCOPe and CATH databases suggests that nowadays state-of-the-art single-sequence-based protein structure prediction methods are still unable to provide reliable predictions for a number of known protein topologies although these proteins have been included in their training sets. More detailed analysis about the imbalanced behaviors of these methods at the level of protein folds and the discussion about the possible reasons could be found in Supplementary Information 1.6. In comparison with the other state-of-the-art methods, SPIRED exhibits a significantly more balanced prediction power at the protein fold/topology level, an advantage that supports its comprehensive competitiveness in facilitating the downstream functional analysis as well as the protein design and engineering.

Remarkable advantage of SPIRED in training time and inference speed

SPIRED significantly prevails OmegaFold and ESMFold in terms of training consumption. As shown in Supplementary Table S11, the training of SPIRED only costs 85 GPU days, in sharp contrast to the 3456 GPU days of OmegaFold (derived from the Supplementary 2.8 and Table S3 of the OmegaFold paper¹²) and the ~896 GPU days of ESMFold (obtained by communication with the first author). Therefore, in comparison to the other state-of-the-art methods, SPIRED effectively reduces the training cost by at least one order of magnitude, mainly through the innovative design on the network architecture and loss function. On the other hand, the number of parameters in the structure prediction module of SPIRED (125M) is in a similar level to that of OmegaFold (124M), both of which are much less than that of ESMFold (690M). Regarding the training samples, both SPIRED and OmegaFold primarily focus on single-chain proteins from the PDB database, supplemented with protein domains from available structural classification databases. In contrast, besides the PDB data, ESMFold also incorporates a large amount of high-quality structures predicted by AlphaFold2 in its training set, which would further exacerbate the training cost.

Based on evaluation upon the model inference speed, we find that SPIRED is approximately 5 times faster than ESMFold and OmegaFold. The time consumption for inferring proteins with length ranging from 100 to 1000 residues on the NVIDIA A100 GPU (80GB) is shown in the Fig. 4. Without recycling, SPIRED takes <1 s when inferring proteins smaller than 400 residues. For example, when inferring a protein of 300 residues, SPIRED takes ~0.5 s, while ESMFold and OmegaFold take 2.7 s and 2.1 s, respectively. For proteins of 600 residues, SPIRED takes ~2.1 s, while ESMFold and OmegaFold take 13.5 s and 12.1 s, respectively. Even when recycling is activated at Cycle = 4, SPIRED still maintains a similar speed advantage in model inference.

Fig. 4: Comparison of inference time.

The horizontal axis represents the length of the proteins, and the vertical axis represents the time taken for inference. In order to generate the plots, protein lengths are discretized into 10 intervals ranging from 100 to 1000 and 4 different proteins are selected in each interval to evaluate the time cost for structure prediction. Source data are provided as a Source Data file.

In summary, the significant advantage of SPIRED in both training cost and inference speed implies its potential in the high-throughput protein structure prediction as well as in the joint training with downstream protein functional prediction models.

Protein fitness prediction by SPIRED-Fitness

Based on the good performance, low training cost and high inference speed of SPIRED, we integrate this model into the protein fitness prediction network and compose an end-to-end framework named SPIRED-Fitness. As mentioned in Methods, we trained the SPIRED-Fitness model primarily using a plethora of multi-labeled DMS data, assisted by PDB data to prevent the potential bias elicited by the limited number of proteins in the DMS dataset. Notably, in the second stage of model training, parameters in the SPIRED module were released for optimization, aiming for further performance improvement by end-to-end training. The final SPIRED-Fitness model takes a single sequence as input and outputs the predicted structure as well as the predicted protein fitness changes caused by all possible single and double mutations in the time scale of seconds for generic proteins.

Here, we compare the fitness prediction performance of SPIRED-Fitness with two well-performed protein fitness prediction models, ECNet³⁶ and GeoFitness v2, using all test data from 485 proteins. Unlike SPIRED-Fitness that only requires the amino acid sequence for inference, ECNet engages evolutionary information from MSA to improve prediction. GeoFitness v2, updated from our prior method GeoFitness v1²⁵, adopts nearly the same model architecture and training procedure with SPIRED-Fitness (Stage 1) but takes the structural information from AlphaFold2 prediction instead. Hence, such comparison can illustrate the role of SPIRED structure prediction and end-to-end training in the protein fitness prediction task. The brief introduction of GeoFitness as well as the modification in GeoFitness v2 and training details could be found in Supplementary Information 3.3. As shown in Table 1, when tested on all single and double mutational data, SPIRED-Fitness exhibits a comparable performance to both ECNet and GeoFitness v2 in terms of the average Spearman correlation coefficient between predicted and experimental values (0.85 vs. 0.84 and 0.83), implying that the precision of SPIRED structure prediction can fulfill the requirement of fitness prediction. Based on detailed protein-wise comparison (Supplementary Fig. S7), SPIRED-Fitness (Stage 2), the end-to-end training version, surpasses both GeoFitness v2 and SPIRED-Fitness (stage 1), the version with frozen SPIRED parameters. Specifically, the end-to-end training in Stage 2 introduces a gain of 2% in the fitness prediction, with only an acceptable minor loss in the structure prediction accuracy (Supplementary Table S2, see Supplementary Information 2.1 for details). This observation further supports the positive impact of end-to-end training frameworks in the protein functional prediction tasks. It is noteworthy that the apparently high performance of ECNet should be less concerned, since ECNet can only process single-labeled data and thus has to be retrained for each specific protein target with known data before inference, whereas both SPIRED-Fitness and GeoFitness v2 are universal models that only need to be trained once using the whole multi-labeled DMS data and are able to provide predictions for unseen proteins. Consequently, during the overall evaluation process, both SPIRED-Fitness and GeoFitness v2 cost significantly less time than ECNet (Table 1), by the avoidance of model retraining. Incidentally, SPIRED-Fitness is faster by 1900 times than GeoFitness v2, because of the highly efficient protein structure prediction by SPIRED in comparison to the AlphaFold2 employed in the GeoFitness pipeline for feature generation.

Table 1 Fitness prediction performance and time consumed for evaluation

The cDNA proteolysis dataset³⁷ and the MaveDB^38,39/DeepSequence⁴⁰ datasets that are used for training SPIRED-Fitness (see “Methods” section) have highly distinct labels: the former is closely related with the protein stability, while the latter ones resemble conventional, diversified DMS data that correspond to various indicators for multiple cellular processes. Moreover, the proteolytic data greatly outnumbers the non-proteolytic data, raising the risk of biased model training. To investigate this potential problem, we reevaluated SPIRED-Fitness against ECNet and GeoFitness v2 within the proteolytic and non-proteolytic types of data, respectively. As shown in Supplementary Table S3, the generally similar level of performance between SPIRED-Fitness and ECNet within each of the two categories of data (in terms of single + double mutations) negates the presence of significant bias elicited by data imbalance during model training, considering that each ECNet model is optimized for one individual protein using one specific set of DMS data. Moreover, finetuning the SPIRED-Fitness model using non-proteolytic data alone brings only negligible changes to the model performance (Supplementary Table S3), further supporting the lack of bias during the model training of SPIRED-Fitness. The apparently weaker Spearman correlation of SPIRED-Fitness within the double mutants is suspected to arise from the design of our training loss function, which is proposed to constrain on the ranking of all mutants within each individual protein without distinguishing the single and double ones. Considering the imbalanced distribution of single and double mutational data among DMS assays (Supplementary Table S4), further model finetuning over assays with sufficient amount of double mutational data may correct this deficit.

Since some methods in the field of fitness prediction only allow inference on single mutational effects, for a broader performance comparison, we trained SPIRED-Fitness using the single mutational data in the training set and evaluated its performance against unsupervised models including RF_joint^17,41, MSA Transformer⁶, ESM-2¹¹, ESM-1b⁵, ESM-1v⁴², and DeepSequence⁴⁰ as well as supervised models including ECNet³⁶ and SESNet¹⁹ also on the single mutational data in the test set. As shown in Supplementary Fig. S8, SPIRED-Fitness outperforms all unsupervised models on the vast majority of proteins and its overall performance is also better than the supervised models (average Spearman correlation coefficient of 0.87 in SPIRED-Fitness vs. 0.83 in ECNet and SESNet). Supplementary Table S5 presents the detailed performance comparison of all of the above methods on the proteolytic and non-proteolytic types of data. Furthermore, we find that as the training sample size decreases, ECNet quickly loses its prediction power, in sharp contrast to the mild decline in the performance of SPIRED-Fitness (Fig. 5a). Particularly, with only 10% of the training samples, the Spearman correlation coefficients of SPIRED-Fitness and GeoFitness v2 still stay above 0.7, while that of ECNet goes below 0.4, indicating that in the few-shot fitness prediction scenarios, SPIRED-Fitness and GeoFitness v2 are much more robust than ECNet, due to the effective utilization of multi-labeled data in model training. To further evaluate the generalizability of SPIRED-Fitness and GeoFitness v2, we conducted 10-fold cross validations, in each experiment of which 80% proteins were chosen for training and validation while 20% unseen protein were left for testing (Fig. 5b). In such a test mimicking the zero-shot prediction scenarios, both SPIRED-Fitness and GeoFitness v2 achieve good performance (median value of the average Spearman correlation efficient > 0.7).

Fig. 5: Detailed analysis of SPIRED-Fitness.

a Comparison of ECNet, GeoFitness v2 and SPIRED-Fitness when trained with various proportions of data on single mutations of 485 proteins. The full training set contains 70% of the single mutational data in the whole dataset, which corresponds to the maximum value on the horizontal axis in the bar chart. Each bar represents the Spearman correlation coefficient averaged over the 485 proteins. b 10-fold cross validation of GeoFitness v2 and SPIRED-Fitness with the protein-specific data splitting. The boxplot is constructed from the results of 10 independent experiments, in each of which 80% proteins are chosen for training/validation and the remaining 20% unseen proteins are used for testing. Each red dot represents the result of one individual experiment. The center line of each boxplot shows the median of the validation results with the value marked aside. The box limits correspond to the upper and lower quartiles, whereas the whiskers extend to 1.5 inter-quartile range. Source data are provided as a Source Data file.

Given the above analysis, the newly developed end-to-end framework SPIRED-Fitness greatly enhances the power and convenience of protein fitness prediction, considering its high accuracy, robustness, broad generalizability, significant speed advantage and bypass of cumbersome feature engineering.

Benchmark of SPIRED-Fitness on ProteinGym

In order to further evaluate the potential role of SPIRED-Fitness in practical protein engineering, we tested SPIRED-Fitness on ProteinGym⁴³, a large-scale and holistic set of benchmarks specifically designed for protein fitness prediction and design. ProteinGym, which contains over 200 standardized DMS assays, allows two testing modes, the supervised setting and zero-shot setting, which are proposed to benchmark protein fitness predictors trained with and without existing DMS labels for a target protein, respectively.

We first evaluated SPIRED-Fitness in the zero-shot setting. The original SPIRED-Fitness only allows the prediction of single and double mutational effects, incapable of handling the triple or higher-order mutational data in ProteinGym. To address this problem, we propose an iterative approach to infer the multiple mutational effects through multiple rounds of SPIRED-Fitness inference on single mutations (Supplementary Fig. S9, see Supplementary Information 2.4.1 for details). Notably, all proteins redundant with the training set of the original SPIRED-Fitness model should be excluded from evaluation in order to guarantee the truly zero-shot benchmarking on unseen proteins. After removing the redundant and/or extra-large proteins, we finally focused on 50 DMS assays for formal analysis. The proteins in these assays meet the following criteria: sequence identity < 50% with the training set of the original SPIRED-Fitness model and length < 900 residues (full list of assays available in Supplementary Data 4). Before the zero-shot prediction of SPIRED-Fitness, we first clustered these ProteinGym assays into 10 groups based on protein sequence similarity, with the maximal inter-group sequence identity < 50%. For the inference on assays of each individual group, we finetuned the original SPIRED-Fitness (Stage 2) model on all assays falling outside the group (i.e. from the other 9 groups). Hence, we produced 10 finetuned SPIRED-Fitness models in total, each of which was purposed as the zero-shot predictor for a specific group of testing assays. In practical fitness prediction on new assays, results of these 10 models could be utilized in ensemble to further improve the reliability of prediction. Here, we compare SPIRED-Fitness with ProteinGym baselines as well as GVP-MSA⁴⁴, a recently proposed method that also allows zero-shot functional prediction. All methods are generally classified into three groups: single-sequence-based, MSA-based, and structure-based. Clearly, SPIRED-Fitness and traditional protein language models fall into the first category, exhibiting marked advantage in inference time over the other two categories, which rely on MSA search either explicitly or implicitly through AlphaFold2 prediction. As shown in Table 2 for the prediction of single mutational effects, at least in terms of the Spearman correlation coefficient, AUC and MCC, SPIRED-Fitness is only slightly inferior to two state-of-the-art MSA-based predictors, TranceptEVE L⁴⁵ and GEMME⁴⁶, and outperforms the other single-sequence-based methods, although the advantage diminishes in the NDCG and the Top 10% recall. Moreover, when evaluated on double, triple and quadruple mutation data (Supplementary Table S6), SPIRED-Fitness achieves satisfying prediction accuracy, ranking among the top within single-sequence-based predictors and exhibiting a comparable performance to VESPA⁴⁷ in general (Supplementary Table S7).

Table 2 Comparison of SPIRED-Fitness with other zero-shot predictors on ProteinGym single mutation data

Subsequently, we evaluated SPIRED-Fitness in the supervised setting on all ProteinGym assays. The single mutational data in ProteinGym assays are split in three different strategies with increasing learning difficulties: Random, Modulo and Contiguous. Conventionally, the ProteinGym supervised predictors should be trained and evaluated by 5-fold cross validation independently for each splitting strategy of each individual assay. Hence, the overall evaluation process of a supervised model on 201 assays typically needs 201 × 3 × 5 = 3015 repeats of model training in total, which is highly laborious and tedious. Unlike the traditional approaches, the design of SPIRED-Fitness allows the training of a universal model for all assays by employing a Soft Spearman Loss⁴⁸ (see Supplementary Information 4.2 for details) to learn the general mutational effects from various DMS indicators. Therefore, for each data splitting strategy and each fold of cross validation, we combined data from all assays to train a unified model and then evaluated its performance on each individual assay. This approach reduces the number of repeated model training from 3015 to 15, greatly simplifying the evaluation process. Here, we compare with strong ProteinGym baselines. Again, all methods are classified into two categories: MSA-based and single-sequence-based. The latter category includes SPIRED-Fitness as well as the ESM-1v and/or One Hot Encoding (OHE) related methods, which make prediction purely based on the amino acid sequence without using any information from MSA. As shown in Supplementary Table S8, SPIRED-Fitness leads the other single-sequence-based methods, outperforms the Augmented linear regression⁴⁹ (i.e. DeepSequence + OHE), a conventional method that explicitly uses the results of MSA-based zero-shot predictors for prediction, and is only behind the state-of-the-art ProteinNPT⁵⁰. Moreover, we slightly modified the architecture of SPIRED-Fitness to allow the prediction of multiple mutational effects (Supplementary Fig. S10a). After optimizing learnable parameters in the appended MLP and output layers using the multiple mutational data (full list of assays available in Supplementary Data 5), SPIRED-Fitness exhibits a satisfactory performance in the supervised learning on the multiple mutational effects (Supplementary Fig. S10b).

Hence, the good performance of SPIRED-Fitness on the ProteinGym benckmark further supports that our SPIRED-Fitness model adequately learns the general mutational effects.

Prediction of the mutational effects on protein stability by SPIRED-Stab

Considering that SPIRED-Fitness effectively learns the general mutational effects, we reutilize its major components in the SPIRED-Stab model to overcome the challenge of limited amount of labeled data for protein stability prediction. As a proof of principle for this idea, we first tested the zero-shot prediction behavior of SPIRED-Fitness on the S669⁵¹/S461⁵² and S557 datasets (see “Methods” section), the conventional test sets for evaluating ΔΔG and ΔT_m prediction methods, respectively. Subsequently, we trained the SPIRED-Stab model using the Dual Task Dataset and then evaluated its prediction behaviors for ΔΔG and ΔT_m prediction tasks on the S669/S461 and S557 datasets, respectively. Notably, during conventional evaluation upon the ΔΔG/ΔT_m predictors, the Spearman/Pearson correlation coefficients are estimated over all variants across proteins in the test set. Such a cross-protein evaluation approach will bring artifacts to the evaluation results, since relative ranking/magnitude of ΔΔG/ΔT_m between variants from different proteins is less informative to the practical protein engineering that typically focuses on mutations within one individual protein. Consequently, in this work, we evaluate metrics like the Spearman correlation coefficient within each individual protein and report the mean and standard deviation of each metric over all tested proteins as its indicator for the overall performance. Exemplar results of the conventional evaluation approach are shown for the S461 dataset in the Supplementary Table S10.

As shown in Table 3, Supplementary Table S9, and Table 4, the zero-shot prediction by SPIRED-Fitness has already surpassed most of the mainstream ΔΔG/ΔT_m predictors, achieving comparable performance to our old version of GeoDDG and GeoDTm that have been sufficiently trained using experimental ΔΔG/ΔT_m labels as well as a few recently proposed methods including ThermoMPNN⁵³, RaSP⁵⁴, PROSTATA⁵⁵, Pythia⁵⁶ and Mutate Everything⁵⁷ in the ΔΔG and ΔT_m prediction tasks. Hence, SPIRED-Fitness has indeed learned the mutational effects from the DMS data fairly well and is capable of predicting the protein stability change with considerable power even in the absence of protein stability data. Furthermore, after sufficient training using the experimental ΔΔG/ΔT_m data, SPIRED-Stab shows an additional performance enhancement as expected. Specifically, SPIRED-Stab and GeoStab v2 (updated from GeoFitness v2 as described in Supplementary Information 3.3) outperform the other methods in nearly all metrics. Noticeably, in comparison to GeoStab v2, SPIRED-Stab is faster by orders of magnitude in practice due to the avoidance of MSA feature generation for AlphaFold2 prediction, in addition to the advantage in performance.

Table 3 Comparison of SPIRED-Stab with other ΔΔG predictors on the S669 dataset

Table 4 Comparison of SPIRED-Stab with other ΔT_m predictors on the S557 dataset

In conclusion, SPIRED-Stab developed from the end-to-end framework SPIRED-Fitness remarkably improves the accuracy and speed for the prediction of protein stability metrics, ΔΔG and ΔT_m, caused by arbitrary mutations.

Discussion

Currently, mainstream single-sequence-based protein structure prediction models exemplified by ESMFold and OmegaFold tend to adopt structure folding modules similar to AlphaFold2 in order to achieve high prediction performance. Albeit successful, this approach also brings new issues. Firstly, models engaging AlphaFold2-type structural folding module require considerable time and vast computational resources to accomplish model training, which nearly precludes the chance of ordinary research groups to update model parameters by retraining, to freely modify the model architecture, and/or to finetune the model for downstream tasks. Secondly, the running time and memory costs of these models are still unsatisfactory, which not only hinders high-throughput inference required by downstream functional analysis, but also prohibits the integration of them with downstream models for end-to-end training. In this work, we introduce an initial endeavor to address this problem. By designing an innovative network architecture (i.e. the Folding Units) for structural modeling and proposing a loss function (i.e. the Relative Displacement Loss) for structural constraining, we successfully reduce the model training consumption in single-sequence-based protein structure prediction algorithms by at least one order of magnitude and improve the model inference speed by 4–5 times. Moreover, our SPIRED model shows a comparable performance to OmegaFold on CAMEO and CASP15 targets, and outperforms both ESMFold and OmegaFold when evaluated on all known protein folds or topologies, targets that are more relevant for the downstream functional analysis as well as the practical protein design and engineering. Our endeavor paves the way for the joint training of sequence-based structure prediction model and structure-based functional prediction network in an end-to-end manner.

The deep learning data in biology exhibits a highly diverse nature. Protein fitness data, encompassing different types of labels such as protein stability, enzyme activity and binding affinity, differ from the single-type labels in language learning and image recognition. The integration of multiple small pieces of data with highly variable labels is crucial for improving the protein fitness prediction. In our prior work on GeoFitness²⁵, we used the Soft Spearman Loss to leverage the multi-labeled data and successfully constructed a universal fitness prediction model with state-of-the-art performance. In this study, we construct a single-sequence version of the fitness prediction model, SPIRED-Fitness, by integrating the structure prediction module SPIRED and the fitness prediction module into an end-to-end framework. By this means, the model inference is accelerated by 1900 folds (in comparison with GeoFitness v2), through bypassing the time-consuming sequence alignment and structural modeling processes of AlphaFold2. More importantly, we demonstrate that the end-to-end training from sequence to structure to function can improve the prediction of single and double mutational effects by around 2% to 3%. Such an end-to-end scheme may be extended to other fields like the protein design, where the joint training of structure-based sequence generation modules and sequence-based structure prediction modules is expected to further improve the foldability of designed sequences.

The mutational effects on protein stability constitute an important problem within the scope of protein fitness. We achieve the state-of-the-art prediction for ΔΔG and ΔT_m in SPIRED-Stab using a Russian-doll-style pre-training approach (Fig. 6). Specifically, SPIRED-Stab is trained by a limited amount of protein stability data, but the SPIRED-Fitness module within this model has been pre-trained by a plethora of DMS data. Similarly, SPIRED-Fitness is trained by multi-labeled DMS data, but the SPIRED module within this model has been pre-trained by vast uniformly labeled PDB data. At the next level, SPIRED is trained by tens of thousands of pieces of protein structure data, but the ESM-2 module within this model has been pre-trained by 65 million pieces of sequence data from UniRef⁵⁸. Through such a hierarchical training scheme, our final SPIRED-Stab model benefits greatly from the comprehensive utilization of data from various sources, e.g., the sequence database, the structure database, the protein fitness data and the protein stability data. Such a pre-training strategy may be extended to the prediction of other biological properties, considering the “fragmented" and “multi-labeled" characteristics of most data in biological and medical sciences.

Fig. 6: The Russian-doll-style pre-training strategy for SPIRED-Fitness and SPIRED-Stab.

The step-by-step pre-training from sequence to structure, and then to fitness, and finally to stability. SPIRED can be regarded as the pre-trained structure model for SPIRED-Fitness, which itself is also the pre-trained model for SPIRED-Stab.

Methods

Network architecture of SPIRED

The SPIRED model mainly consists of four Folding Units (Fig. 1a, Algorithm 1 of Supplementary Information 5.1). When predicting the protein structure, SPIRED only requires the amino acid sequence of the target protein, which is encoded into high-dimensional embedding (1D information) by the ESM-2¹¹ language model. The sequence embedding is then fed into the Folding Units, in each of which 1D and 2D information mutually updates and multiple sets of coordinates of C_α atoms are predicted. Unlike mainstream methods like AlphaFold2 and ESMFold that employ the 1D information to predict the atom coordinates in the global coordinate system (i.e. the laboratory coordinate system in which a protein structure is determined experimentally), in each Folding Unit of SPIRED, the 2D information is used to predict a total of L (i.e. the number of residues) sets of relative coordinates for the C_α atoms, each taking the local coordinate system of an individual residue (i.e. the coordinate system in which C_α atom is placed at the origin, C atom is placed on the x-axis and N atom is placed in the xy plane) as the reference frame. Since both outputs and labels (i.e. relative C_α coordinates in individual local frames) are ro-translationally invariant, our design avoids the equivariant operations that usually augment the computational complexity. The multiple sets of C_α coordinates predicted by the last Folding Unit, along with pLDDT and main-chain torsional angles (also composed of 2D matrices), are passed to GDFold2³¹, an in-house folding algorithm based on gradient descent optimization, for main-chain adjustment and side-chain packing, resulting in the full atomic coordinates of the protein.

The network structures of the first three Folding Units are essentially the same. Here, we take Folding Unit1 (Fig. 1b, Algorithm 2 of Supplementary Information 5.1) as an example to illustrate the basic network architecture of Folding Units. For Folding Unit1, the 1D feature is the sequence embedding provided by ESM-2 and the 2D feature is initialized as a zero-valued tensor. While for the other Folding Units, the input 1D and 2D features are generated by the preceding Folding Unit. Within a Folding Unit, the 1D and 2D features are first updated by the Triangular Self-Attention module^7,11,59. The new 1D feature is directly passed on to the next Folding Unit, whereas the updated 2D feature goes through Instance/Row/Column Normalization operations⁶⁰ (I/R/CN in Fig. 1b, Algorithm 4 of Supplementary Information 5.1), followed by the coordinate prediction module Pred-XYZ (Algorithm 5 of Supplementary Information 5.1). The first Pred-XYZ module predicts the absolute C_α coordinates and generates a new 2D feature that is passed on to the next Pred-XYZ module, while the second Pred-XYZ module predicts additional corrections to the C_α coordinates. The two Pred-XYZ modules have shared parameters. The pairwise distances between C_α atoms are then calculated from the predicted coordinates (Algorithm 6 of Supplementary Information 5.1). The distance matrix, along with the 2D feature, is then passed to ConvBlock (Algorithm 7 of Supplementary Information 5.1), resulting in a new 2D feature that enters the next Folding Unit.

The network architecture of Folding Unit4 (Algorithm 3 of Supplementary Information 5.1) is slightly more complex than the other Folding Units as it engages six Pred-XYZ modules for coordinate prediction and updates, where the first four Pred-XYZ modules and the last two Pred-XYZ modules are constrained by two slightly different versions of the RD Loss (see Algorithm 11 and Algorithm 12), respectively, and are thus designed to have two separate sets of shared weights. The coordinates updated by the last Pred-XYZ module in Folding Unit4 serve as the final C_α coordinates.

In addition, the 2D feature generated by Folding Unit4 is also utilized to predict the C_β distance distribution, dihedral and scalar angles quantifying inter-residue orientation (Algorithm 8 of Supplementary Information 5.1) as well as main-chain torsion angles (Algorithm 9 of Supplementary Information 5.1). Incidentally, each Folding Unit has the capacity to predict pLDDT (Algorithm 10 of Supplementary Information 5.1), and we consider the pLDDT values output from Folding Unit4 as the representative ones. Finally, since the sequential arrangement of multiple Folding Units yield similar benefits for structure refinement akin to the recurrent expansion by recycling (Supplementary Fig. S1, see Supplementary Information 1.1 for details), recycling is abandoned by default (i.e. Cycle = 1) to accelerate inference but could be optionally activated (e.g., Cycle = 4) in SPIRED.

Relative displacement loss in SPIRED

During the training process of SPIRED, the RD Loss (Fig. 1c, Algorithms 11 and 12 of Supplementary Information 5.2) is utilized to constrain the C_α coordinates predicted by each Folding Unit. RD Loss is a loss function that is designed to achieve the constraining role of the FAPE Loss⁷ in a computationally less intensive manner. In comparison to the FAPE Loss, it circumvents the laborious coordinate alignment and the costly prediction of rotation matrices, but focuses on evaluating the average prediction accuracy of relative displacement vectors between each pair of C_α atoms in the multiple reference local coordinate systems.

Before calculating the RD Loss, a local coordinate system is established for each individual residue, where C_α is set as the origin and the basis vectors are determined from the positions of C_α, C and N atoms, following the AlphaFold2⁷ definition. SPIRED predicts the C_α coordinates of all residues in each local reference frame. As shown in Fig. 1c, in the local coordinate system of residue k, the relative displacement between a pair of residues i and j is evaluated for the predicted structure (${\overrightarrow{\tilde{x}}}_{ij}={\overrightarrow{\tilde{x}}}_{kj}-{\overrightarrow{\tilde{x}}}_{ki}$) and the ground truth (${\overrightarrow{x}}_{ij}={\overrightarrow{x}}_{kj}-{\overrightarrow{x}}_{ki}$), respectively. The RD Loss is then computed as the difference between the predicted and ground truth vectors averaged over all residue pairs and over all reference frames. In contrast, almost all mainstream structure prediction models (e.g., AlphaFold2, ESMFold and OmegaFold) use the FAPE Loss, which requires predicting quaternions to achieve rotation and laboriously aligning the predicted and true coordinates. Although the offsets between predicted and true coordinates are also evaluated in the FAPE Loss, the inter-residue relative displacement ${\overrightarrow{\tilde{x}}}_{ij}$ is not specifically considered. Therefore, the RD Loss brings two advantages for training the structure prediction model. Firstly, the RD Loss avoids predicting the rotation matrices, only requiring the prediction of relative positions between residues, thereby alleviating the difficulty of model training of SPIRED. Secondly, the RD Loss places more focuses on the relative displacement between residues, a metric that is more intensively correlated with the inter-residue vibrations rather than the global translation and rotation.

Besides the RD Loss, the inter-residue distance and angle distribution losses are computed based on the C_β distance distogram as well as the dihedral and scalar angles of all residue pairs following the trRosetta⁶¹ definition and are utilized as auxiliary losses for the training of SPIRED. In addition, the C_α distance loss (Algorithm 13 of Supplementary Information 5.2), pLDDT loss (Algorithm 14 of Supplementary Information 5.2) and C_α clash loss (Algorithm 15 of Supplementary Information 5.2) are also computed as auxiliary losses. Details about the implementation and combination of these losses are described in Supplementary Information 4.1.

Network architecture of SPIRED-Fitness and SPIRED-Stab

The SPIRED-Fitness model engages ESM-2 and SPIRED as the extractors for 1D and 2D information, respectively (Fig. 1d). The downstream Fitness Module is mainly composed of the Geometric Encoder that adopts the Graph Attention Network (GAT) architecture (Algorithms 16, 17 and 18 of Supplementary Information 5.3) to iteratively update the node and edge features provided by ESM-2 and SPIRED. Specifically, the node feature is initialized by the sequence embedding of ESM-2 (650M), whereas the edge feature includes the multiple sets of C_α coordinates and the pLDDT values predicted by SPIRED. The updated node and edge features are then fed into MLP (i.e. multiple layer perceptron) layers for the prediction of fitness changes caused by single and double mutations, respectively. Notably, in the prediction of single mutational effects, the fitness landscape is generated from the 1D MLP output in combination with the ESM-1v⁴² logits (i.e. logits before Softmax operation in the last output layer of the ESM-1v model), following the procedure of our prior work in GeoFitness v1²⁵ (see Supplementary Information 3.3 for a brief introduction). As for the prediction of double mutational effects, the fitness scores of all possible mutations for each residue pair are predicted from each individual term of the 2D MLP output directly.

Since the SPIRED-Fitness model could be sufficiently optimized by the abundant DMS data to learn the general mutational effects, reutilization of SPIRED-Fitness modules in SPIRED-Stab would effectively overcome the challenge of limited amount of data in the protein stability prediction. A similar idea has been validated in our prior work on GeoDDG/GeoDTm v1²⁵ (see Supplementary Information 3.3 for a brief introduction). Specifically, majority of the SPIRED-Fitness model (ESM-2, SPIRED and the Geometric Encoder, as enclosed by a dashed box in Fig. 1d) is directly implanted into SPIRED-Stab with the same network architecture and parameters, followed by MLP layers for the prediction of stability score (Algorithms 19 and 20 of Supplementary Information 5.3). Noticeably, SPIRED-Stab retains shared weights for the two channels of inputs, i.e. the wild-type and mutant sequences, and the difference of their prediction scores is then scaled to predict the absolute values of ΔΔG and ΔT_m, a similar design to our prior GeoDDG/GeoDTm v1 models that intrinsically guarantees the antisymmetry of prediction results.

Training set for SPIRED structure prediction

First, we collected protein structures available until March 2022 from the PDB²⁹ database, but filtered out the structural files with >5 polypeptide chains and with resolution >5 Å. Then, we split the remaining structures into multiple single chains and retained chains with length between 40 and 1,200 residues. Next, we clustered these chains using MMseqs2⁶² easy-cluster with the sequence identity threshold of 100% and only kept the representative chains of clusters, which finally resulted in 113,609 chains. We also utilized domain structures from the CATH³⁵ database (v4.2, S35) as supplementary training data, which contained 24,183 domains with length ranging from 63 to 600 residues.

Training process for SPIRED structure prediction

As shown in Supplementary Table S12, the training process of SPIRED is mainly divided into four stages, during which the learning difficulty is continually enhanced (e.g., by including hard protein samples or increasing the cropping size), allowing the model to grasp the protein sequence-structure relationship gradually. Technical details of the four stages are shown as follows:

First stage, we performed clustering on 101,915 polypeptide chains (before May 2020) with 30% sequence identity using MMseqs2, which resulted in 24,179 clusters. We trained SPIRED for ~10,000 update steps with the clustered PDB chains, where one chain was iteratively chosen from every cluster in each epoch. During this process, the learning rate was linearly warmed up from 10⁻⁶ to 10⁻³ in the first 1,000 updates, retained at the peak value of 10⁻³ for the next 6,500 updates, and declined down to 5 × 10⁻⁴ for the final 2500 updates.

Second stage, we selected an “easy subset" with length <400 residues and resolution <3 Å from the whole training set. We then trained SPIRED with the ~63,000 “easy subset" chains for ~8,000 updates. The learning rate was declined from 5 × 10⁻⁴ to 10⁻⁴ in this stage.

Third stage, we used the whole training set, containing 113,609 PDB chains (before March 2022) and 24,183 CATH domains, to train SPIRED for ~23,000 updates, with the learning rate annealed from 10⁻⁴ to 5 × 10⁻⁵. The cropping size was kept at 256 in the first three stages.

Fourth stage, we trained SPIRED for 18,000 updates with the cropping size expanded to 350, and kept the cropping size at 420 for the next 12,000 updates. The learning rate was annealed from 5 × 10⁻⁵ to 10⁻⁵ during this stage.

The batch size was fixed to 64 and the Adam optimizer was used throughout the training process of SPIRED.

Test sets for protein structure prediction

We used two test sets to evaluate the performance of structure prediction methods. The first test set was constructed from CAMEO²⁶ targets (August 2022  ~ August 2023), consisting of 680 protein chains with the length ranging from 50 to 1,126 residues (Supplementary Data 6). The second test set was composed of 45 protein domains released from the CASP15²⁸ official website (Supplementary Data 7).

We used two kinds of structure classification databases, SCOPe³³ database (v2.08, S95, September 2021) and CATH³⁵ database (v4.2, S35, July 2017), to evaluate the structure prediction power on different types of protein backbone folds or topologies. We selected domains from SCOPe with length ranging from 50 to 800 residues, resulting in 1231 folds and 34,021 domains in total. Similarly, 1223 topologies and 24,183 domains were collected from CATH.

Training and test sets for protein fitness prediction

We utilized DMS data to train and test fitness prediction models, which included data from three different sources.

cDNA proteolysis dataset³⁷. Tsuboyama et al. constructed a library in which mutated proteins were covalently linked to cDNA. These proteins were subsequently subjected to proteolysis, and the cDNA fragments connected to those proteins that were not cleaved could be detected through sequencing, allowing the determination of the quantity of intact proteins at different protease concentrations. Due to the fact that mutated proteins with lower folding stability are more susceptible to proteolytic cleavage in the experiment, protein ΔG values can be estimated using protein cleavage rate data and Bayesian inference. This experimental method facilitates the large-scale analysis of the impact of mutations on protein stability, enabling the examination of folding stability across 900,000 protein domains in a week. From the data provided in the article, we selected 412 proteins with length ranging from 32 to 72 residues to compose a dataset for protein fitness prediction. Of these proteins, 153 proteins have data for both single and double mutations, while the rest only have data for single mutations.

MaveDB^38,39 is a database that contains fitness data of mutated proteins obtained from DMS experiments and massively paralleled reporter assays, including enzymatic activity, binding affinity, etc. We selected 51 proteins from MaveDB for the training and testing of our models.

DeepSequence Dataset⁴⁰ collects fitness data of mutated proteins from DMS experiments. After filtering out data that are redundant with the MaveDB database, we finally retained 22 proteins from this dataset for the subsequent fitness training and testing purposes.

Details of the combined MaveDB/DeepSequence datasets could be found in Supplementary Data 8. The data from all of the three aforementioned sources collectively constituted a dataset of 485 proteins, consisting of ~693,000 single mutations and ~265,000 double mutations. For each protein, all fitness data were randomly assigned for training, validation and testing with a ratio of 7:1:2.

Training process for SPIRED-Fitness

The training of SPIRED-Fitness could be mainly divided into two stages.

In the first stage, the SPIRED parameters were frozen and only parameters of the Fitness Module were updated for ~400 epochs. The learning rate was initially set to 10⁻³ and was adjusted following the learning rate scheduler of ReduceLROnPlateau (factor = 0.5, patience = 10). The Fitness Module corresponding to the best performance of the fitness prediction on the validation set was used for continued training in the next stage (Fitness Module hyper-parameters: node_dim = 32, pair_dim = 32, N_head = 8, N_block = 2, see Algorithms 17 and 18 of Supplementary Information 5.3). When calculating the loss of this training stage, single mutations and double mutations are combined as a comprehensive mutation set. The Soft Spearman Loss⁴⁸ (see Supplementary Information 4.2 for details) between the predicted fitness scores and the ground truth values is computed within this mutation set (Eq. (1)).

$${{{\rm{Fitness}}}}\_{{{\rm{Loss}}}}={{{\rm{Soft}}}}\_{{{\rm{Spearman}}}}\_{{{\rm{Loss}}}}(\{{{{\rm{single}}}}\_{{{\rm{mutation}}}}\}\cup \{{{{\rm{double}}}}\_{{{\rm{mutation}}}}\})$$

(1)

In the second stage, both the SPIRED module and the Fitness Module were allowed to update parameters, using training data from two sources: the structural data and fitness data. The structural data were initially taken from the training set of the fourth training stage of SPIRED (Supplementary Table S12) with lDDT >0.5 (~133,000 protein chains), and were then randomly shuffled and divided into 133 subsets, each of 1000 samples. The fitness data were the DMS data used in the first stage. For each epoch of the training process, the samples included one subset of structural samples and nearly all fitness samples (from 482 proteins after excluding 3 large proteins with length > 800 residues), in total of 1482 proteins. After training over all structural samples by 133 epochs, SPIRED-Fitness was finetuned on CPU for the three large proteins excluded previously from the fitness samples. The learning rate for the SPIRED module was fixed at 10⁻⁵, while that for the Fitness Module was initialized to 10⁻⁴ and then manually adjusted to 10⁻⁵. The loss for this stage is represented by the Union Loss defined in Eq. (2): the Structural Loss alone was applied for the structural samples, while the joint loss of structure and fitness was applied for the fitness samples. The Structure Loss took the same form as that used in the SPIRED model training (see Supplementary Information 4.1 for details), but was scaled by a weight of 0.05.

$${{{\rm{Union}}}}\_{{{\rm{Loss}}}}=\left\{\begin{array}{ll}0.05\times {{{\rm{Struct}}}}\_{{{\rm{Loss}}}} \hfill \quad &({{{\rm{Structure}}}}\,{{{\rm{data}}}})\\ 0.05\times {{{\rm{Struct}}}}\_{{{\rm{Loss}}}}+{{{\rm{Fitness}}}}\_{{{\rm{Loss}}}}\quad &({{{\rm{Fitness}}}}\,{{{\rm{data}}}}) \hfill \end{array}\right.$$

(2)

Training and test sets for protein stability prediction

The datasets utilized for training and testing in SPIRED-Stab are described in detail here.

Dual Task Dataset is a dataset constructed in this work for the training of SPIRED-Stab. We collected single, double and triple or higher-order mutation data of both ΔΔG and ΔT_m from two protein stability databases, ProThermDB⁶³ and ThermoMutDB⁶⁴, and cautiously cleaned each piece of data to generate the dataset for the ΔΔG/ΔT_m dual task training of SPIRED-Stab. The final dataset contains 8458 pieces of single mutation data, 966 pieces of double mutation data and 619 pieces of triple or higher-order mutation data (i.e. mutation points ≥3), where 5331 pieces of data only have the ΔΔG label, 2560 pieces of data only have the ΔT_m label and 2152 pieces of data have both ΔΔG and ΔT_m labels.

S669⁵¹ is a widely used test set to assess the accuracy of ΔΔG prediction. This dataset consists of 669 single-point mutations derived from 94 proteins selected from ThermoMutDB (v1.3). These proteins have sequence similarity of < 25% with the proteins in the S2648 and VariBench databases that have been extensively used as training data in many previous researches.

S461⁵², a subset of S669 dataset with the errors manually corrected, contains 461 single-point mutations. The S461 dataset is used as an auxiliary benchmark test dataset to evaluate ΔΔG prediction.

S557 is a subset of S571 dataset constructed in our previous work²⁵ to specifically address the ΔT_m evaluation problem. We no longer consider pH values, and thus have removed redundancy from the original dataset. This dataset now contains 557 pieces of single mutation data, and is used as an objective benchmark test dataset to evaluate the ΔT_m prediction.

Training process for SPIRED-Stab

The training of SPIRED-Stab could be divided into three stages. In all training stages, we adopted the Adam optimizer and the learning rate would decline by half if the validation loss did not decrease for five consecutive epochs.

In the first stage, the model parameters of SPIRED-Fitness (except for the MLP module) were used as the starting point of SPIRED-Stab. The training dataset was the cDNA proteolysis dataset described above, and the Soft Spearman Loss was used to evaluate the Spearman correlation coefficient between the predicted ΔΔG and the experimental values. The initial learning rate of this stage was 10⁻³ and all parameters except the final ΔΔG_coef and ΔT_m_coef parameters (Algorithm 19) were optimized.

Since the ΔΔG values in the cDNA proteolysis dataset are derived from Bayesian inference, it is necessary to train the model on the ΔΔG/ΔT_m dataset with experimentally measured values. In the second stage, SPIRED-Stab was further trained on our collected and curated ΔΔG/ΔT_m dataset, namely the Dual Task Dataset, with the Soft Spearman Loss employed for the optimization of ranking correlation. In this stage, the MLP layer for the ΔΔG prediction was optimized with the initial learning rate of 5 × 10⁻⁴ and the corresponding value for the ΔT_m prediction was 5 × 10⁻³ (Fig. 1e).

In the third stage, the numerical difference between the predicted and experimentally determined ΔΔG/ΔT_m values was computed, following the Mean Squared Error (MSE) Loss. During the training in this stage, the majority of the parameters of SPIRED-Stab were frozen, and only the final ΔΔG_coef and ΔT_m_coef parameters were updated with an initial learning rate of 10⁻², aiming for matching the predicted values towards the actual ΔΔG/ΔT_m distribution without perturbing the learned ranking of mutational effects.

Evaluation metrics

In this study, we utilize TM-score and lDDT to assess the similarity between predicted and true protein structures. Besides, we mainly employ the Spearman correlation coefficient to assess the prediction power of the tested models on fitness, ΔΔG and ΔT_m values. Specifically, we examine the correlation between the predicted scores and the experimental fitness/ΔΔG/ΔT_m for different mutations.

TM-score³² (Template Modeling score) is a metric used to assess the topological similarity between protein structures. The protein structure of interest (i.e. target) is aligned to a reference structure (i.e. template), and the root-mean-square-deviation (RMSD) of the aligned residue pairs is calculated. According to Eq. (3), TM-score ranges from 0 to 1, with the value of 1 indicating a perfect match between structures. TM-score is more sensitive to the global topology than to local structural difference, with the value below 0.17 as an indicator of lack of relationship between the protein structures and a value greater than 0.5 as an indicator of belonging to the same topology.

$${{{\rm{TM}}}}-{{{\rm{score}}}}={{{\rm{Max}}}}\left[\frac{1}{{L}_{N}}{\sum}_{i=1}^{{L}_{r}}\frac{1}{1+{(\frac{{d}_{i}}{{d}_{0}})}^{2}}\right],$$

(3)

where d_i represents the distance between the i^th aligned residue pairs, d₀ is a normalization scale, L_N denotes the original length of the protein, and L_r represents the number of aligned residues.

lDDT⁶⁵ (local Distance Difference Test) is a superposition-free score that indicates the difference in local inter-residue distances between the predicted structure and reference structure. First, the distance (L_true) between each pair of atoms in the reference structure is calculated, excluding distances beyond the threshold R₀ and atoms within the same residue. The distances (L_pred) between corresponding atom pairs are then computed for the predicted structure. Next, the absolute difference in distances between the two structures for each atom pair is calculated (Diff = $\left\vert {L}_{true}-{L}_{pred}\right\vert$). The counts of atom pairs with Diff values below four thresholds (0.5, 1, 2, and 4 Å) are calculated, and the average of these counts divided by the total number of atom pairs produces the lDDT score. In this study, we only calculate the lDDT score for C_α atoms (lDDT-C_α) with R₀ = 15 Å.

Pearson correlation coefficient (r) is a measure used to quantify the strength of the linear relationship between two variables, X and Y. As shown in the Eq. (4), it is computed by calculating the ratio of the covariance between the two variables to the product of their standard errors. The coefficient ranges from −1 to 1, where −1 indicates a perfect negative correlation, 0 indicates no correlation, and 1 indicates a perfect positive correlation.

$${{{{\boldsymbol{r}}}}}_{X,Y}=\frac{{{{\rm{cov}}}}(X,Y)}{{\sigma }_{X}{\sigma }_{Y}},$$

(4)

where cov denotes the covariance and σ stands for the standard deviation (i.e. the square root of variance).

Spearman correlation coefficient (ρ) is commonly used to describe the strength of a monotonic relationship between two variables. As shown in the Eq. (5), Spearman correlation coefficient is calculated by utilizing the ranked values of a pair of variables (X, Y). This characteristic makes the Spearman correlation coefficient more robust to outliers in the data.

$$\begin{array}{rc}{{{{\boldsymbol{\rho }}}}}_{X,Y}={{{{\boldsymbol{r}}}}}_{{{{\rm{R}}}}(X),{{{\rm{R}}}}(Y)}&=\frac{{{{\rm{cov}}}}({{{\rm{R}}}}(X),{{{\rm{R}}}}(Y))}{{\sigma }_{{{{\rm{R}}}}(X)}{\sigma }_{{{{\rm{R}}}}(Y)}},\end{array}$$

(5)

where R denotes the ranking operation for the variables.

Kendall correlation coefficient (τ) is another non-parametric metric to measure the correlation between ranks of the variables and can be interpreted as the probabilities of observing the agreeable (concordant) and non-agreeable (discordant) pairs (Equation (6)). The Kendall correlation coefficient is more robust than the Spearman correlation coefficient while usually being smaller in magnitude.

$$\tau=\frac{{n}_{c}-{n}_{d}}{{n}_{c}+{n}_{d}},$$

(6)

where n_c denotes the number of concordant pairs while n_d denotes the number of discordant pairs.

Top K precision is a metric measuring the fraction of the truly top K mutations among the predicted top K mutations (Equation (7)). This metric serves as a reference for the success rate in the real-world protein engineering process.

$${{{\rm{Top}}}}\,{{{\rm{K}}}}\,{{{\rm{precision}}}}=\frac{{\sum }_{i}^{n}{I}_{1\le rank({\hat{Y}}_{i})\le K}{I}_{1\le rank({Y}_{i})\le K}}{{\sum }_{i}^{n}{I}_{1\le rank({\hat{Y}}_{i})\le K}},$$

(7)

where $rank({\hat{Y}}_{i})$ and rank(Y_i) denote the rank (in descending order) of the predicted value and that of the label, respectively, and I is the indicator function.

NDCG (Normalized Discounted Cumulative Gain) is a metric in ProteinGym⁴³ for evaluating the fitness prediction methods. Suppose that the top K scores provided by a predictor are sorted in descending order as ${\hat{Y}}_{1}\ge {\hat{Y}}_{2}\ge \cdots \ge {\hat{Y}}_{K}$. DCG (Discounted Cumulative Gain) reports the sum of corresponding true labels by discounting each term according to its predicted rank:

$${{{\rm{DCG}}}}=\mathop{\sum}_{i}^{K}\frac{{Y}_{i}}{{\log }_{2}(i+1)},$$

(8)

where Y_i is the true label for the i^th ranking variant among the top K predictions. NDCG normalizes DCG of a predicted rank by ideal DCG, which is calculated similarly to DCG but with a perfect ranking based on true labels. The metric encourages models to accurately rank higher fitness values in earlier positions.

Top 10% recall is a metric adopted by ProteinGym⁴³ for fitness prediction evaluation, which reports the proportion of truly Top 10% variants among the Top 10% predictions. Its definition is identical to Equation (7), except that K refers to a specific ratio of 10%.

AUC, the abbreviation of the area under a receiver operating characteristic (ROC) curve, is a metric adopted by ProteinGym⁴³ for measuring the binary classification performance of models. The value of AUC ranges from 0.5 to 1, where 0.5 and 1 correspond to random and perfect classifications, respectively.

MCC (Matthews correlation coefficient) is a metric adopted by ProteinGym⁴³ for evaluating the performance of binary and multiclass classifications. The true and false positives/negatives are considered in the calculation of MCC. The value of MCC ranges from -1 to 1, where -1 represents a reverse prediction of classification, 0 stands for a random prediction, and 1 refers to perfect classifications. For the binary classification, the calculation of MCC is proceeded in the following manner:

$${{{\rm{MCC}}}}=\frac{({{{\rm{TP}}}}\times {{{\rm{TN}}}})-({{{\rm{FP}}}}\times {{{\rm{FN}}}})}{\sqrt{({{{\rm{TP}}}}+{{{\rm{FP}}}})({{{\rm{TP}}}}+{{{\rm{FN}}}})({{{\rm{TN}}}}+{{{\rm{FP}}}})({{{\rm{TN}}}}+{{{\rm{FN}}}})}},$$

(9)

where TP, FP, TN, and FN represent the numbers of true positives, false positives, true negatives and false negatives, respectively.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.