Not all oil types are alike in trade substitution

Abstract

Motivated by the ongoing war in Ukraine and the public debate on sanctioning crude oil imports from Russia, we estimate the elasticity of substitution between different crude oil types. Using European data on country-level crude oil imports by their field of origin, we argue that crude oil is far from a homogenous good, and that the relevant substitutability for analyzing the impact of trade sanctions must account for the quality of different oil types in terms of their density and sulfur content. Distinguishing crude oil imports by their chemical composition, the elasticity of substitution between types is substantially lower than suggested by previous estimates. Our results also suggest that, by neglecting these differences in quality, standard estimates underestimate the production disruptions and price effects in crude oil refining resulting from sanctions.

Introduction

Following the Russian Federation’s invasion of Ukraine, many countries, including the European Union (EU), have adopted trade-related sanctions against Russia. Due to the EU’s reliance on Russian oil and gas, the debate on sanctioning these commodities attracted widespread attention by the media and policymakers alike. Political considerations regarding the economic viability of sanctions hinge on the volume of energy imports that must be replaced and the substitutability of Russian oil and gas imports through direct replacement or alternative energy sources. An aspect widely ignored in the debate of sanctions against Russia are disparities in quality between and within different types of crude oil.

Our analysis relates to the existing literature that considers different oil types as imperfect substitutes in the evaluation of economic policies. Çakır Melek et al.¹ estimate substitution elasticities between light and heavy crude oil in order to investigate the economic effects of the U.S. shale oil boom and crude oil export ban. Several other studies also focus on the U.S. economy^2,3, leaving a gap in our understanding of the European market. The recent EU sanctions on crude oil imports from Russia have raised questions about their consequences. Although EU crude oil imports from Russia may have been partially replaced with U.S. exports, most studies on the impact of energy sanctions ignore the fact that not all oil types are alike⁴. Given the importance of the elasticity of substitution for both the welfare gains from globalization as well as the welfare losses from sanctions^5,6,7 and the importance of oil trade and consumption², our results inform the political debate on sanctioning Russian crude oil and other commodities with similar characteristics.

From an economic perspective, crude oil quality matters because “light” (i.e. high API gravity) crude oil yields a larger share of high-value refined products and because removing sulfur — the most common impurity of crude oil — is costly. A profit-maximizing refinery tries to minimize the costs of its intermediate inputs, while maximizing the output share of refined products that are currently in high demand. Moreover, the equipment installed or layout of a refinery determines the range of processable crude slates — the mix of crude oils used by refineries as an input in the production process.

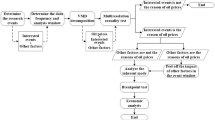
From a technical perspective, petroleum refineries transform crude oil into refined products, which are used as transportation fuels (i.e. kerosene, diesel, gasoline), heating oil, bitumen, and petrochemical feedstock⁸. When crude oil enters the refinery, it is desalted, heated, and separated into different fractions in the distillation column. The distillation unit determines the volume a refinery can process, as all crude oil needs to go through the distillation step (Fig. 1). The resulting proportions of each fraction depend on the crude oil quality — mainly its density, which is measured by API gravity. The higher the quality of the crude oil, the higher the yield of premium distilled products, such as gasoline. As a result, low-quality crude oil trades at a discount in global markets. Speight⁹ provides an extensive discussion on the chemical composition of crude oil.

Fig. 1: Refinery process.

Simplified illustration inspired by U.S. Energy Information Administration (EIA)⁸ and Gary et al.¹⁰. Favennec⁴⁰ estimates that the costs of building a new complex refinery with a capacity of 160,000 b/d in Europe in 2022 was approximately $6 billion, while a simple refinery (i.e. just distillation column) with a capacity of 100,000 b/d would cost about $3 billion.

To increase the output share of high-margin products, such as gasoline or diesel, refineries aim at upgrading low-value fractions in the conversion process by the use of cokers, alkylation, reforming, or some kind of cracking unit¹⁰. Although the installation of cracking and coking units is costly, they greatly increase the efficiency and flexibility of a refinery with regard to processable crude slates, whereas simple refineries without conversion units (a.k.a. topping refineries) are much more restricted with respect to the slates they can process. Given that they produce a larger share of low-margin heavy fuel oil, these refineries are less common today and mainly used in remote areas for the production of industrial fuels or to prepare feedstocks for the petrochemical industry.

The last refining step discussed here is desulfurization. Due to environmental regulations and for technical considerations, crude oil impurities in general must be removed in the refining process. The most common impurities in crude oil are sulfur compounds⁹, which cause oxidation and reduce thus the lifespan of a refinery. Removing sulfur is costly, as it requires refineries to use high temperature and pressure as well as hydrogen. For both technical and cost reasons, refineries therefore prefer crude slates with low sulfur content.

The above description, although simplified, emphasizes that crude oil is not a homogenous input in the refining process. On the one hand, sulfur impurities are costly to remove and accelerate attrition. On the other hand, higher-density crude oil yields a large share of low-margin refined products from distillation and must therefore be upgraded, which is costly and requires the installment of a conversion unit. For example, recent crude assays by BP¹¹ indicate that distillation of Iraqi Basrah Heavy (23.7^∘ API gravity) yields 57.2% of low-value residual fuels, whereas distillation of the global benchmark Brent crude (38^∘ API density) yields only 39.7% of residual fuels.

We use comprehensive country-level data on EU crude oil imports to show that the elasticity of substitution between crude oil types is much lower than suggested by previous estimates. While crude oil is commonly regarded as a standardized commodity, in reality, it is far from homogenous, owing to the variability in its chemical composition. The data we use contains detailed information on the density (i.e., low or high API gravity) and the sulfur content (i.e., “sweet” or “sour”) of oil varieties across different fields of origin. This allows us to group crude oils by their chemical composition into technically heterogeneous oil types and disentangle the elasticities of substitution within and between these types.

In this work, we contribute to the existing literature in four key dimensions. First, we provide estimates for the elasticity of substitution between different crude oil types that explicitly account for its chemical composition. Second, we link this to the recent policy debate of EU sanctions on crude oil imports from Russia, acknowledging the fact that crude oil varies in its chemical composition and, hence, its quality. Third, we leverage EU data on crude oil imports by country to estimate country-specific elasticities of substitution between different types of crude oil. Fourth, we quantify the importance of our estimates for production and prices in the refining sector associated with a crude oil import ban.

Results

Table 1 reports the coefficient estimates of a hedonic pricing model, where we regress the import price of crude oil on quality characteristics and observables that are typically included in gravity models of international trade. The price differential between heterogeneous crude oil types has been studied extensively in the prior literature^12,13,14.

Table 1 Hedonic pricing model

Based on our previous discussion, all else equal, higher API gravity should be associated with a higher crude oil price, as lighter crude oil yields a larger share of high-value refined products. Conversely, higher sulfur content should be associated with a lower crude oil price, as removing impurities is costly for refineries. Including time, importer, and exporter fixed effects, the respective coefficient estimates reported in Table 1 have the expected signs, are highly statistically significant and economically relevant. For example, comparing Brent crude (38^∘ API gravity, 0.4% sulfur content) and Basrah Heavy (23.7^∘ API gravity, 4.12% sulfur content), the latter trades at an average discount of 6.22$/bbl in our sample.

Definition of goods and varieties

To avoid a confounding effect of differential exchange rate dynamics during our sample period and to ensure the comparability of country-level estimates, we focus on crude oil imports of Euro Area member states in what follows. While applying a widely used method introduced by Feenstra¹⁵ to calculate the elasticity of substitution, we depart from the original Armington¹⁶ assumption that different varieties of the same good are identified by their countries of origin. To gauge the effects of sanctioning oil imports from Russia or other major oil-exporting countries on production, we instead define different varieties of crude oil by their objectively measurable chemical composition. Following Broda and Weinstein¹⁷, we then estimate the elasticity of substitution between these heterogeneous crude oil types.

We measure crude oil quality along two dimensions — API gravity and sulfur content. To categorize similar crude oil types, practitioners usually differentiate between light, medium, and heavy as well as sweet and sour crude oil, where light indicates a low density (i.e. high API gravity) and sweet indicates low sulfur content.

Figure 2 illustrates different aggregation methods using the EU Crude Oil Import Register (COIR). Panel (a) depicts Euro Area crude oil imports over the entire sample period by field of origin. Accordingly, each symbol refers to a specific oil field, while the size of the symbol indicates the volume of crude oil imported from this field. Simply applying Feenstra’s¹⁵ methodology to the disaggregated data addresses the question of how easily crude oil imports from any field can on average be replaced by crude oil imports from any other field.

Fig. 2: Different product/variety specifications for Euro Area crude oil imports.

a Crude oil imports by field of origin. Russian Urals accounts for the majority of medium-sour imports. b Crude oil imports aggregated by country of origin. Kazakhstan is the largest single provider of light-sweet crude oil. c Light-sweet crude oil imports by field of origin³⁵. d Crude oil imports by oil type. Euro Area refineries strongly depend on Russia for medium-sour imports, while Kazakhstan accounts for less than a fifth of total light-sweet imports.

Following Armington¹⁶ and Feenstra¹⁵, we aggregate crude oil imports by their country of origin in panel (b). Different varieties of crude oil are then defined at the country level. Given that more than one oil field may be located on the same country’s territory, the number of varieties decreases relative to panel (a).

In the spirit of Blonigen and Soderbery¹⁸, we can classify light sweet crude oil as a separate good and define different varieties of light sweet crude oil by their fields of origin, which may be located in different countries. This is shown in Panel (c). Broda and Weinstein¹⁷ refer to this as the “within-product elasticity of substitution”.

Panel (d) depicts our preferred definition of varieties based on the chemical composition of different crude oil types. Rather than differentiating varieties of the heterogeneous good crude oil by their countries or fields of origin, we aggregate crude oil imports into five economically meaningful types, which arguably reflect their quality and have different chemical properties in the refining process. In contrast to panel (c), which speaks to the within-type elasticity of substitution, this allows addressing the question of how easily one can replace imports of medium-sour crude oil (indicated by the light-blue square) by imports of light sweet crude oil (indicated by the orange circle), for example. In light of the recent debate on sanctions, this seems to be the relevant elasticity of substitution when it comes to quantifying the cost of replacing Russian Urals — a medium-sour type, for which there are few within-type substitutes available — by other crude oil types.

Elasticities of substitution

We estimate the substitution elasticity of crude oil for each aggregation method shown in Fig. 2. Table 2 reports the estimated elasticities for three different specifications of crude oil varieties by oil field, country of origin, and oil type, respectively, for selected EU countries in the COIR data set.

Table 2 Elasticities of substitution for different product/variety specifications

In the Oil Field column, we distinguish varieties by their fields of production, at the most granular level available in the COIR data set, and estimate elasticities of substitution across all oil types. While it is difficult to form priors on the values of the substitution elasticities, given the granularity of varieties, we would expect these estimates to be higher than for the other two levels of aggregation. Except for Austria, our estimates indeed tend to be high and, considering the confidence bands, imprecisely estimated.

Using Feenstra’s original approach and distinguishing crude oil varieties by their countries rather than fields of origin, our point estimates tend to drop significantly, albeit not for all countries in our sample. These values are directly comparable with estimates previously reported in the literature^2,6.

Considering our specification of crude oil types in the third column, the estimated elasticities of substitution are even lower. Estimates of the order in the third column of Table 2 suggest potentially non-trivial welfare effects of an expansion or shrinkage of this set. Given that Russian Urals accounts for the vast majority of medium-sour imports in the COIR data set (see Fig. 3), some EU countries effectively lose access to this oil type, if Russian pipeline imports are banned, as well. Assuming that the crude slate of refineries in the EU was conditionally optimal before the adoption of sanctions, as they benefited from cheap Russian crude oil, the former would be confronted with a narrower set of varieties or higher costs of importing Saudi Arabian medium-sour or U.S. light-sweet crude oil via vessels. According to Alan Gelder, Wood Mackenzie’s lead downstream analyst, the ideal replacement for Russian crude would be Arab light oil, which is actually a medium density oil type. However, with Saudi Arabian production stalling, EU refineries have switched to lighter grades such as US crude. In either case, this leads to inefficiencies due to a sub-optimal crude slate and more costly transport over longer distances (Table 1).

Fig. 3: Distribution of Euro Area imports for the two most common crude oil types.

Total crude oil imports during our sample period (2013–2019) are shown. Dotted-bars refer to medium-sour and striped bars refer to light-sweet crude oil imports. Russian imports of the two types are highlighted in red and blue, respectively.

In what follows, we compare our approach with that in Feenstra¹⁵. In particular, we show that the implications of the two approaches for refinery production and prices may differ substantially and what this depends on. In international economics, it is common practice to consider the change in product varieties when calculating consumer welfare. Given that several studies^6,15 report welfare gains due to an increase in available varieties, this is also known as the “gains from variety”. Sanctions instead lead to a reduction in the available set of varieties and thus to a potential welfare loss.

Approximation of production disruptions

Our first exercise is inspired by the production theory of Ethier¹⁹, who assumes that downstream producers — in our case refineries — prefer a larger variety of inputs to enhance their productivity. In line with our previous approach, we modify the functional-form assumptions in Ethier¹⁹ and allow for a nested constant-elasticity-of-substitution (nested CES) type production function, similar to Çakır Melek et al.¹, where we distinguish the substitutability of crude oil varieties within and between nests, and each nest corresponds to a different oil type. The final output of country c’s oil sector is a nested CES aggregate of oil varieties:

$${Y}_{c}={\left[{\sum}_{g\in {{\boldsymbol{\Omega }}}}{\left({\sum}_{v\in {{{\bf{V}}}}_{g}}{q}_{gv}^{\frac{\sigma -1}{\sigma }}\right)}^{\frac{\sigma }{\sigma -1}\cdot \frac{\gamma -1}{\gamma }}\right]}^{\frac{\gamma }{\gamma -1}}$$

(1)

where q_gv denotes the processed quantity of oil variety v ∈ V_g in oil type (nest) g ∈ Ω. Individual oil varieties (i.e. different oil fields) may be more substitutable within the same oil type than against other oil types (if γ < σ) or less substitutable (if γ > σ). Our empirical results, however, clearly suggest the former case. This has important implications when analyzing the abrupt stop of oil imports of a certain region as a result of sanctions. The ultimate impact on Y_c depends on whether a representative refinery in country c retains access to close alternative substitutes within the same oil type or whether the imposed sanctions are equivalent to the loss of access to an oil type. To fix ideas and focus on the role of changes in the availability of varieties versus oil types, we abstract here from heterogeneity in quantities of oil varieties. This allows us to rewrite Eq. (1) as

$${Y}_{c}={{{\boldsymbol{\Omega }}}}^{\frac{\gamma }{\gamma -1}}{{{\bf{V}}}}^{\frac{\sigma }{\sigma -1}}q.$$

(2)

Inspecting Eq. (2) immediately shows that the elasticity of production with respect to changes in nests (Ω) or varieties (V) depends on the substituability parameters γ and σ. The respective elasticities are given by $\frac{d\ln {Y}_{c}}{d\ln {{\boldsymbol{\Omega }}}}=\frac{\gamma }{\gamma -1}$ and $\frac{d\ln {Y}_{c}}{d\ln {{\bf{V}}}}=\frac{\sigma }{\sigma -1}$, which are only identical for γ = σ. This is the implicit assumption made by Feenstra¹⁵. In all other scenarios, the results will differ from the case with only one elasticity of substitution, with the deviations increasing in the difference between γ and σ.

In a final step, we apply these theoretical considerations to our empirical results. Table 3 contrasts Feenstra estimates of the CES elasticity based on the Country of Origin from Table 2 with our estimates based on the characterization by Oil Type and the nested CES production technology in Eq. (1). Column 1 refers to the standard CES case, where σ ( = γ) represents the elasticity of substitution between crude oil imported from different countries. In columns 2 and 3, we report the average within-type elasticity (Supplementary Table 2) for the nested CES case as well as the elasticity of substitution between different crude oil types (γ). In all cases, we find that γ < σ, indicating a lower substitutability between than within nests, and hence a more significant impact on production in case of the loss of access to an entire oil type.

Table 3 Approximation of production disruptions

This can be seen in column 4, where we investigate the hypothetical scenario of a loss of access to medium-sour crude oil (i.e. a complete nest). This is relevant, given that a ban of Russian oil comes close to the latter scenario for countries where Russian Urals accounts for the largest fraction of total medium-sour oil imports. In column 5, we remove crude oil imports (of any type) from Russia.

The reported values correspond to differential changes in production in percentage points between the standard CES and the nested CES case, where we subtract the former from the latter. Accordingly, a negative value indicates that the implied change in production is larger when assuming a nested CES structure and our estimates for the within- and between-type elasticities, which is always the case. The predicted losses in production from removing all imports of medium-sour crude oil in Euro Area refineries, for example, are 4.74 percentage points larger when accounting for the fact that not all oil types are alike. This pattern of underestimating the disruptions in production from sanctioning crude oil imports from Russia is consistent across both scenarios and for all countries and regions in Table 3. Since some of the oil supplied by Russia is Siberian light sweet crude, which can be more easily substituted by light sweet imports from other countries, the difference is smaller in the scenario of a complete halt of crude oil imports from Russia. The difference between the two scenarios tends to be smaller for countries that mainly import medium-sour crude oil from Russia and have a low estimated elasticity of substitution.

While the scenarios in columns 4 and 5 are based on actual expenditure shares for 2013–2019, prior to the COVID-19 pandemic and the Russian invasion of Ukraine, they do not account for the potential replacement of crude oil imports from Russia in the data. For this reason, column 6 reports the differential production losses when accounting for actual changes in import quantities across types between 2021 and 2023 — before and after the introduction of a price cap on Russian crude oil. For all (groups of) countries, production losses are larger when allowing for a nested CES production structure and the associated elasticity estimates in columns 2 and 3 than in the standard CES case, reaching 7.9 percentage points for Germany.

The four panels of Fig. 4 plot total EU crude oil imports by their chemical composition aggregated to annual data for 2020, 2021, 2022, and 2023, respectively, and illustrate that the partial loss of access to a particular oil type — namely medium sour — was not merely a hypothetical scenario. The rectangles and bubbles in red indicate the quality and quantity of medium sour Urals and light sweet Siberian crude oil imports from Russia. While the volume of these imports hardly changed between 2021 and 2022, after the Russian invasion of Ukraine, and imports of Siberian actually increased, imports of both Urals and Siberian came to a near halt between 2022 and 2023, after the EU’s adoption of sanctions against Russia in December 2022.

Fig. 4: Total EU crude oil imports by quality characteristics before and after the introduction of sanctions.

Panels a and b refer to 2020 and 2021, respectively – the years preceding the sanctions. Panels c and d refer to 2022 and 2023, respectively – the years during and following the adoption of sanctions. In all panels, Russia is highlighted in red.

Figure 4 also shows that the EU was not able to compensate this shortfall by raising imports of medium sour crude oil from other countries of origin (light-blue rectangles). Instead, the quantity of all medium sour imports decreased substantially after the adoption of sanctions against Russia.

Input costs in refinery production

In a second exercise, we quantify the price effects of sanctioning crude oil imports from Russia with standard and nested CES production, respectively. Given that crude oil is primarily used as an input into refinery production rather than directly consumed by households, we derive an exact import price index of EU refineries to account for the loss of access to some crude oil varieties.^6,15,18,20 The construction of the price index is described in detail in the Methods section.

Table 4 reports the change in this index between 2021 and 2022 and between 2022 and 2023 in columns 1 and 2, respectively, for the CES case with homogeneous crude oil and the nested CES case, which allows for different substitutability of crude oil varieties between and within oil types. In either case, we use our empirical estimates of the substitution elasticities for the Euro Area from Table 2 and Supplementary Table 2. In columns 3 and 4, we present an extension of the conventional nested CES price index with oil type-specific tastes, where we hold tastes constant at their pre-COVID levels. This alternative approach is based on the notion that sanctions represent exogenously imposed rather than voluntary changes in refineries’ optimal crude slate. Accordingly, a deviation from the optimal slate incurs a penalty on the import price paid by refineries. The details of the approach are described in the Methods section. In Table 4, we also report the observed import price change (i.e. the volume-weighted change in prices of crude oil imports) and the average change in the price of diesel relative to gasoline across EU member states for the same periods.

Table 4 Exact crude oil import price index for the Euro Area

The steep increase in the observed import price by 42.9% between 2021 and 2022 is almost perfectly reflected by the change in the exact price index in the CES case. In the nested CES case, the exact price index increases slightly less. Splitting up this increase, we find that the nested structure attenuated the increase in the exact price index by about 3.2% due to favorable adjustments in the composition of imports across oil types.

Following the decline in global oil prices between 2022 and 2023, the observed COIR import price also dropped, despite the adoption of sanctions on crude oil imports from Russia in December 2022. While this drop is again closely replicated in the CES case, the exact price index decreases by only 6% in the nested CES case, as about half of the negative contribution within types is offset by the positive contribution between types.

With fixed tastes, the aggregate change in the exact price index between 2021 and 2022 is smaller than observed in the CES case and larger than observed in the nested CES case, indicating that the nested structure exacerbates the increase in the average COIR import price. Between 2022 and 2023, after the adoption of crude oil sanctions, the nested CES price index with fixed tastes displays a much smaller decrease compared to both the standard CES price index and the observed import price change.

Assuming that the composition of crude oil imports prior to the sanctions reflected the optimal crude slate of Euro Area refineries, the imperfect substitutability across crude oil types, the lack of alternative sources of medium sour crude oil, and the resulting change in the composition of imports between 2022 and 2023 implies a muted reduction in the exact price index relative to that of world crude oil prices.

Discussion

Our estimates suggest that the substitutability between oil types is much lower than within oil types. As shown in Table 3, this has important implications for evaluating EU sanctions on crude oil imports from Russia. Russian Urals served as an important medium-sour benchmark for European refineries that is more technically challenging and thus more expensive to replace. Figure 4 further illustrates that EU member states effectively lost access to medium sour crude oil after the start of sanctions in December 2023. Given that crude oil is used almost exclusively as an intermediate input in the refining process rather than consumed directly, these sanctions impair the “ideal set” of a refinery’s crude slate and thus consumer welfare indirectly through higher prices of refined petroleum products, given that refineries pass through changes in production costs to consumer prices²¹.

As conjectured by Bachmann et al.⁴, Fig. 5a shows that EU countries redirected their crude oil imports towards the U.S. after the Russian invasion of Ukraine. At the same time, Fig. 5b illustrates that there is very little overlap in quality characteristics between recent crude oil imports from Russia and the U.S. Crude oil imports from Russia with an average API gravity of 31^∘ and a sulfur content of 1.52% were replaced by imports from the U.S. with an average API gravity of 42^∘ and a sulfur content of 0.24%. These differences in the chemical composition have two major disadvantages for European refineries. First, U.S. crude oil trades at a premium and causes thus higher input costs. Fitted values derived from our hedonic pricing model (Table 1) suggest a price differential of 3.23$/bbl. Second, although of higher quality, U.S. crude oil yields less diesel and jet fuel but more gasoline than the previously imported Russian type²². Given the comparatively larger market share of diesel fuel in Europe, this presents a non-trivial concern. Accordingly, the replacement of Russian Urals with U.S. light sweet crude oil implies economically relevant deviations from the optimal crude slate and potential reconfiguration costs of refineries, similar to those faced by U.S. refineries after the shale oil revolution³. According to Ed Scardaville from U.S. consultancy Baker & O’Brien, losses in distillate production of a full-conversion complex refinery may reach up to 7% after switching from Russian Urals to WTI²², consistent with our estimates for Germany in Table 3.

Fig. 5: European crude oil imports from the United States and Russia before and after the start of the EU crude oil embargo.

a Time series of imported volumes from Russia and the U.S. into the EU. b Chemical composition of crude oils imported from Russia [blue squares] in the year before the sanctions and chemical composition of U.S. imports [red bubbles] in the first year of the oil embargo. The size of the symbols refers to the volume of crude oil imports.

Although these costs accrue to EU refineries rather than consumers directly, they are reflected by the average change of diesel fuel relative to gasoline prices. After the start of sanctions against Russia and the effective loss of access to medium sour crude oil (Fig. 4), which has a higher boiling point and yields a larger share of diesel fuel²³, the relative price of diesel increased in the vast majority of EU member countries and by 8.2% on average (Table 4). This suggests that the higher input costs in refinery production due to the involuntary deviation from the optimal crude slate were passed on to EU consumers in the form of higher output prices, in particular of diesel fuel.

Methods

To estimate the elasticity of substitution between different crude oil types, we apply the econometric approach proposed by Feenstra¹⁵ and later refined by Broda and Weinstein⁶. This method has been widely discussed in the literature^24,25,26,27. We use this methodology for two reasons. First, it is widely used in empirical work^28,29. Second, it allows for heterogeneity in the substitution elasticity across countries. Çakır Melek et al.¹ follow an alternative approach using simulated method of moments to estimate substitution elasticities between light and heavy crude oil and investigate the effects of the U.S. shale oil boom and crude oil export ban in a calibrated general-equilibrium model of the world economy.

Feenstra¹⁵ and Broda and Weinstein⁶ are interested in estimating an exact aggregate price index to study the gains from trade due to a larger set of varieties, we focus on estimating the elasticity of substitution between imported varieties of the same good. Feenstra et al.³⁰ refers to this as the micro-elasticity of substitution. We first explain the econometric method intuitively below before discussing it in detail.

Intuition

Feenstra’s approach uses a General Method of Moments (GMM) identification via heteroskedasticity of supply and demand shocks, which goes back to the standard identification problem. Given data on prices and quantities but no additional information on external shocks, supply and demand elasticities cannot be identified uniquely³¹. Feenstra¹⁵ recognizes that by adding another dimension to the data, namely differences in varieties, we obtain a panel data set, which allows for estimating supply and demand elasticities. Intuitively, one can estimate a hyperbola of optimal supply and demand elasticities for each variety. Assuming that the elasticity of substitution is constant across varieties and that the same holds for the supply elasticity, the true estimator is given by the intersection of the hyperbolas. A sufficient condition for the applicability of Feenstra’s approach is that the hyperbolas are not the same across varieties. It can be shown that the curve for each variety depends on the variances and covariances of supply and demand shocks, which in turn depend on macroeconomic fluctuations. As long as some of the economies that a country imports from face different macroeconomic shocks, efficient estimates can be obtained.

Estimating substitution elasticities

In the following, we describe the estimation procedure of the elasticity of substitution. We start our formal exposition with Feenstra’s generalized version of the minimum cost function:

$$c\left({\pi }_{t},\,{{{\bf{V}}}}_{t},\,{{{\bf{b}}}}_{t}\right)={\left[{\sum}_{v\in {{{\bf{V}}}}_{t}}\left({b}_{vt}{\lambda }_{v,\,t-1}/{\lambda }_{vt}\right){P}_{vt}^{1-\sigma }\right]}^{1/(1-\sigma )},$$

(3)

where

$${\lambda }_{r}\equiv {\sum}_{v\in {{\bf{V}}}}{p}_{vr}{m}_{vr}/{\sum}_{v\in {{{\bf{V}}}}_{r}}{p}_{vr}{m}_{vr}\, {{\rm{for}}}\, r=t-1,\, t.$$

In (3), v refers to a specific variety in the set V_t available in period t, σ is the elasticity of substitution, and b_v,t denotes a variety-specific (random) taste or quality parameter. π_t refers to the exact price index and is equal to the conventional price index $P\left({{{\bf{p}}}}_{t-1},\,{{{\bf{p}}}}_{t},\,{{{\bf{m}}}}_{t-1},\,{{{\bf{m}}}}_{t},\,{{\bf{V}}}\right)$, which ignores new product varieties, times the additional term ${\left({\lambda }_{t}/{\lambda }_{t-1}\right)}^{1/(\sigma -1)}$. λ_t denotes the fraction of expenditure on goods available in both periods relative to the expenditure on goods available in period t. p_v and m_v refer to prices and quantities of variety v, respectively. Since we only consider non-oil-producing countries, we will also refer to m_v as import volumes. Note that Feenstra¹⁵ distinguishes varieties by their countries of origin¹⁶.

From the minimum cost function in (3), we can derive the import demand equation for each variety, which is expressed in the first differences of import shares:

$$\Delta \ln {s}_{vt}={\phi }_{t}-(\sigma -1)\Delta \ln {P}_{vt}+{\varepsilon }_{vt},\,$$

(4)

where ${\phi }_{t}\equiv (\sigma -1)\ln \left[c\left({\pi }_{t},\, {{{\bf{V}}}}_{t},\, {{{\bf{b}}}}_{t}\right)/c\left({\pi }_{t-1},\, {{{\bf{V}}}}_{t-1},\, {{{\bf{b}}}}_{t-1}\right)\right]$ is a random effect, because b_t is random, and ε_vt = Δln(b_vtλ_vt/λ_v,t−1) appears as an error term. We use shares s_vt rather than quantities, given that the former are not affected by potential measurement error³².

The export supply equation is given by

$$\Delta \ln {P}_{vt}={\psi }_{t}+\rho {\varepsilon }_{vt}/(\sigma -1)+{\delta }_{vt},\,\quad 0 \, \le \, \rho \, < \, 1,\,$$

(5)

where ${\psi }_{t}=\omega \left({\phi }_{t}+\Delta \ln {E}_{t}\right)/(1+\omega \sigma )$ is a random effect, δ_vt ≡ ξ_vt/(1 + ωσ) is the error, ρ ≡ ω(σ − 1)/(1 + ωσ) and ω denotes the inverse supply elasticity (assumed to be the same across varieties). ξ_vt is the random error from the supply equation expressed in quantities rather than shares and assumed to be independent of ε_vt. Hence, δ_vt and ε_vt are assumed to be independent.

Note that ϕ_t and ψ_t depend on time only. It is therefore convenient to define a reference variety k and difference Eqs. (4) and (5) relative to variety k. Accordingly,

$${\tilde{\varepsilon }}_{vt}={\Delta }^{k}\ln {s}_{vt}+(\sigma -1){\Delta }^{k}\ln {P}_{vt},\,$$

(6)

$${\tilde{\delta }}_{vt}=(1-\rho ){\Delta }^{k}\ln {P}_{vt}-\frac{\rho }{\sigma -1}{\Delta }^{k}\ln {s}_{vt},\,$$

(7)

where Δ^kx_vt = Δx_vt − Δx_kt, ${\tilde{\varepsilon }}_{vt}\equiv {\varepsilon }_{vt}-{\varepsilon }_{kt}$ and $\tilde{{\delta }_{vt}}\equiv {\delta }_{vt}-{\delta }_{kt}$.

To take advantage of the independence of ${\tilde{\varepsilon }}_{vt}$ and ${\tilde{\delta }}_{vt}$, we multiply Eqs. (6) and (7) and divide by (1 − ρ)(σ − 1) > 0 to obtain

$${({\Delta }^{k}\ln {P}_{vt})}^{2}={\theta }_{1}{({\Delta }^{k}\ln {s}_{vt})}^{2}+{\theta }_{2}({\Delta }^{k}\ln {s}_{vt})\times ({\Delta }^{k}\ln {P}_{vt})+{u}_{vt},\,$$

(8)

where

$${u}_{vt}=\frac{{\tilde{\varepsilon }}_{vt}{\tilde{\delta }}_{vt}}{(1-\rho )(\sigma -1)},\,\quad {\theta }_{1}\equiv \frac{\rho }{{(\sigma -1)}^{2}(1-\rho )},\,\quad {{\rm{and}}}\quad {\theta }_{2}\equiv \frac{(2\rho -1)}{(\sigma -1)(1-\rho )}.$$

The problem with Eq. (8) is that the error term, u_vt, is correlated with the dependent variables. By exploiting the panel structure of the data together with the assumption that demand and supply elasticities are constant across varieties, consistent estimates can nevertheless be obtained. The variance of the error term in Eq. (8) depends on the variety v. Thus, we need to correct for heteroskedasticity in order to obtain efficient estimates.

Calculating the CES and nested CES price index

To measure the impact of the EU sanctions on crude oil imports from Russia, we calculate the exact price index¹⁵ for European refineries based on a CES and a nested CES production function, respectively. Feenstra¹⁵ generalizes the exact price index of a single good, while taking new and disappearing varieties into account. In the CES case, we follow the same approach, where crude oil is treated as a homogeneous product and each country of origin is assumed to provide one distinct variety. In the nested CES case, we adapt Feenstra’s method for each oil type (e.g. light sweet crude oil), while the varieties correspond to the oil fields that provide this specific oil type. To calculate the aggregate price index for the nested CES production function, we aggregate across the individual price indices and account for the change in the expenditure share of each nest²⁰.

First, we discuss the calculation of the exact price index. Following Feenstra, we focus on the following CES production function:

$${M}_{gt}={\left({\sum}_{v\in {{\bf{V}}}}{b}_{gvt}^{\frac{1}{\sigma }}{m}_{gvt}^{\frac{\sigma -1}{\sigma }}\right)}^{\frac{\sigma }{\sigma -1}},\,\quad \sigma \, > \, 1,\,$$

(9)

where g refers to the good under consideration (i.e. crude oil in the CES case and, for example, light sweet crude oil in the nested CES case) and σ represents the elasticity of substitution between countries of origin (CES) and between oil fields that provide the same type of crude oil (nested CES).

The unit cost requirement resulting from Eq. (9) is given by

$${\phi }_{gt}\left({{{\bf{V}}}}_{gt},\, {{{\bf{b}}}}_{gt}\right)={\left({\sum}_{v\in {{{\bf{V}}}}_{gt}}{b}_{gvt}{p}_{gvt}^{1-\sigma }\right)}^{\frac{1}{1-\sigma }},\,\quad \sigma \, > \, 1,\,$$

(10)

where V_gt denotes the good-specific variety set that is available in the current period, and b_gt is a good-specific vector of taste shocks.

Taking variety change into account, we define the exact price index, π, such that

$$\frac{{\phi }_{gt}\left({{{\bf{V}}}}_{gt},\, {{{\bf{b}}}}_{g}\right)}{{\phi }_{g,\,t-1}\left({{{\bf{V}}}}_{g,\,t-1},\, {{{\bf{b}}}}_{g}\right)}= {\pi }_{gt}\left({{{\bf{p}}}}_{gt},\, {{{\bf{p}}}}_{g,\,t-1},\,{{{\bf{m}}}}_{gt},\,{{{\bf{m}}}}_{g,\,t-1},\,{{{\bf{V}}}}_{g}\right)\\ = {P}_{gt}\left({{{\bf{p}}}}_{gt},\,{{{\bf{p}}}}_{g,\,t-1},\,{{{\bf{m}}}}_{gt},\,{{{\bf{m}}}}_{g,\,t-1},\,{{{\bf{V}}}}_{g}\right)\cdot {\left(\frac{{\lambda }_{gt}}{{\lambda }_{g,\,t-1}}\right)}^{\frac{1}{{\sigma }_{g}-1}},$$

where V_g = V_gt ∩ V_g,t−1 denotes the set of varieties that are available in both periods. The first term P_gt( ⋅ ) corresponds to the “conventional" price index proposed by Sato³³ and Vartia³⁴ defined as

$${P}_{gt}\left({{{\bf{p}}}}_{gt},\, {{{\bf{p}}}}_{g,\,t-1},\, {{{\bf{m}}}}_{gt},\,{{{\bf{m}}}}_{g,\,t-1},\,{{{\bf{V}}}}_{g}\right):={\prod}_{v\in {{{\bf{V}}}}_{g}}{\left(\frac{{p}_{gvt}}{{p}_{gv,\,t-1}}\right)}^{{w}_{gvt}\left({{{\bf{V}}}}_{g}\right)}.$$

This price index corresponds to the geometric mean variety price change, weighted by the ideal log-change weight for each variety:

$${w}_{gvt}\left({{{\bf{V}}}}_{g}\right):=\frac{\left(\frac{{s}_{gvt}-{s}_{gv,\,t-1}}{\ln {s}_{gvt}-\ln {s}_{gv,\,t-1}}\right)}{{\sum}_{v\in {{{\bf{V}}}}_{g}}\left(\frac{{s}_{gvt}-{s}_{gv,\,t-1}}{\ln {s}_{gvt}-\ln {s}_{gv,\,t-1}}\right)}$$

where ${s}_{gvr}:=\frac{{p}_{gvr}{m}_{gvr}}{{\sum }_{v={{{\bf{V}}}}_{g}}{p}_{gv}{m}_{gvr}}$ is the variety cost share in period r. The λ-ratio in the exact price index adjusts the “conventional" price index for new and disappearing varieties, and λ is defined as

$${\lambda }_{gr}=\frac{{\sum }_{v\in {{{\bf{V}}}}_{g}}\, {p}_{gvr}{m}_{gvr}}{{\sum }_{v\in {{{\bf{V}}}}_{gr}}\, {p}_{gvr}{m}_{gvr}}.$$

Thus, the adjustment of the conventional price index will be stronger the larger the λ-ratio and the smaller the elasticity of substitution, σ. While the λ-ratio covers the change in varieties, the elasticity of substitution accounts for the substitutability between different varieties (i.e. crude oil imports from different countries of origin in the CES case).

Second, we discuss the calculation of the nested CES aggregate price index. In the nested CES case, we assume that the aggregate unit expenditure function is given by the CES aggregate of Equation (10) for each oil type g ∈ Ω:

$${P}_{t}={\left[{\sum }_{g \in {{\boldsymbol{\Omega }}}}{B}_{gt}{P}_{gt}^{1- \gamma }\right]}^{\frac{1}{1- \gamma }},\, \quad \gamma \, > \, 1,$$

where γ denotes the elasticity of substitution between different nests (i.e. oil types), and B_gt denotes an oil type-specific taste parameter. Depending on the transport infrastructure, layout of its refineries, or market share of a particular refined product (e.g. diesel), a country might be more or less inclined to import a certain type of crude oil.

Following Redding and Weinstein²⁰ and applying Shephard’s Lemma to the aggregate unit expenditure function, the aggregate expenditure share on oil type s_gt is given by

$${s}_{gt}=\frac{{B}_{gt}{P}_{gt}^{1-\gamma }}{{\sum}_{g\in {{\boldsymbol{\Omega }}}}{B}_{gt}{P}_{gt}^{1-\gamma }}=\frac{{B}_{gt}{P}_{gt}^{1-\gamma }}{{P}_{t}^{1-\gamma }}.$$

Rearranging this expenditure share, and taking logarithms, we obtain the following expression for the aggregate unit expenditure function:

$$\ln {P}_{{{\rm{t}}}}=\ln {P}_{gt}-\ln {B}_{gt}+\frac{1}{\gamma -1}\cdot \ln {s}_{gt}.$$

Differencing over time and averaging across oil types, the change in the aggregate cost of crude oil in refinery production can be expressed as the following exact CES price index:

$$\Delta \ln {P}_{t}=\frac{1}{| {{\boldsymbol{\Omega }}}| }\cdot {\sum}_{g\in {{\boldsymbol{\Omega }}}}\Delta \ln {P}_{gt}+\frac{1}{\gamma -1}\cdot \frac{1}{| {{\boldsymbol{\Omega }}}| }\cdot {\sum}_{g\in {{\boldsymbol{\Omega }}}}\Delta \ln {s}_{gt},\,$$

where we normalize the oil type-specific taste parameters to have a constant geometric mean across oil types:

$$\frac{1}{| {{\boldsymbol{\Omega }}}| }\cdot {\sum}_{g\in {{\boldsymbol{\Omega }}}}\ln \left(\frac{{\phi }_{gt}}{{\phi }_{g,\,t-1}}\right)=0.$$

Third, we discuss the calculation of the nested CES price index with constant tastes. As a robustness check, we furthermore construct the conventional nested CES price index, while keeping oil type-specific tastes constant at their pre-COVID levels. This alternative approach is based on the notion that sanctions represent exogenously imposed rather than voluntary changes in refineries’ optimal crude slate. For this reason, it would be misleading to interpret changes in the expenditure shares of different oil types as changes in tastes over time. To mitigate anticipation effects and pandemic-related disturbances, we calculate average tastes for our baseline period from 2013 to 2019. This extended time frame also helps to reduce the impact of short-lived fluctuations in expenditure shares on our analysis.

Within each nest (i.e., oil type), we assume that the tastes for all varieties are identical. This assumption is based on the homogeneity of crude oil grades within types and supported by the high within-type elasticity estimates in Supplementary Table 2.³⁵

Consider the nested CES production function

$$Y={\left[{\sum}_{g\in {{\boldsymbol{\Omega }}}}{B}_{g}^{\frac{1}{\gamma }}{\left({\sum}_{v\in {{{\bf{V}}}}_{g}}{b}_{gv}^{\frac{1}{\sigma }}{m}_{gv}^{\frac{\sigma -1}{\sigma }}\right)}^{\frac{\sigma }{\sigma -1}\frac{\gamma -1}{\gamma }}\right]}^{\frac{\gamma }{\gamma -1}},\,$$

(11)

where b_gv: = ∣V_g∣⁻¹ due to the assumption of identical tastes for all varieties within each nest.

Assuming perfect competition in the refining market, a representative refinery maximizes

$${{\Pi }}=PY-C=P{\left[{\sum}_{g\in {{\boldsymbol{\Omega }}}}{B}_{g}^{1/\gamma }{\left({\sum}_{v\in {{{\bf{V}}}}_{g}}{b}_{gv}^{1/\sigma }{m}_{gv}^{\frac{\sigma -1}{\sigma }}\right)}^{\frac{\sigma }{\sigma -1}\frac{\gamma -1}{\gamma }}\right]}^{\frac{\gamma }{\gamma -1}}-{\sum}_{g\in {{\boldsymbol{\Omega }}}}{\sum}_{v\in {{{\bf{V}}}}_{g}}{m}_{gv}{p}_{gv}$$

with respect to the optimal import quantity of variety v of type g. Rearranging the corresponding first-order condition yields the (conventional) nested CES price index

$$P={p}_{gv}{\left(\frac{{m}_{gv}}{{b}_{gv}}\right)}^{1/\sigma }{({B}_{g}Y)}^{-1/\gamma }{Y}_{g}^{\frac{\sigma -\gamma }{\sigma \gamma }}$$

(12)

where ${Y}_{g}:={\left({\sum }_{v\in {{{\bf{V}}}}_{g}}{b}_{gv}^{\frac{1}{\sigma }}{m}_{gv}^{\frac{\sigma -1}{\sigma }}\right)}^{\frac{\sigma }{\sigma -1}}$ denotes the component of production due to nest (i.e. oil type) g.

Now consider the optimal choice of quantities at the nest level, Y_g. In this case, the outer part of the nested CES production function can be written as

$$Y={\left[{\sum}_{g\in {{\boldsymbol{\Omega }}}}{B}_{g}^{\frac{1}{\gamma }}\cdot {Y}_{g}^{\frac{\gamma -1}{\gamma }}\right]}^{\frac{\gamma }{\gamma -1}}.$$

(13)

Maximizing the refinery’s profit function with respect to Y_g rather than m_gv and solving for the nest-specific taste B_g yields

$${B}_{g}={\left(\frac{{P}_{g}}{P}\right)}^{\gamma }\cdot \frac{{Y}_{g}}{Y},\,$$

(14)

where P_g denotes the nest-specific price index. We can solve for each B_g numerically and compute the price index for the years 2021–2023 using nest-specific tastes for our baseline sample period, 2013–2019, as outlined in Equation (12).

Data

We use data from the European Commission’s (EC) Crude Oil Import Register (COIR), which mandates EU member countries to report their crude oil imports by field of origin. The data are available on a monthly basis for January 2013 through December 2019. Due to the volatility of crude oil imports at the monthly frequency and to facilitate a comparison with estimates of substitution elasticities for crude oil in the existing literature, the data is time-aggregated to annual frequency. It is important to note that the prices reported in the EC’s COIR are Cost, Insurance, and Freight (CIF) prices. Accordingly, our estimates of substitution elasticities reflect the quality dimension of crude oil as well as a country’s geographical location and the transport infrastructure in place.

Regarding the measurement of quality, the COIR data has a key advantage over standard trade data. EU member countries must report their crude oil imports by field of origin along with their defining characteristics, in particular the API gravity and sulfur content. Where quality information is missing, we obtain supplementary information from various sources, such as the McKinsey Energy Insight and the Energy Information Administration. However, quality assignment is not perfect, as some imports are classified as Other Crude Oil from Country X. The most critical case in terms of volume is Russia, where countries either report imports of Urals Crude Oil or other Russian Crude Oil. Labeling all Other Russian Crude Oil as Siberian Light Sweet — the second largest type produced in Russia — would result in unreasonably high imports of the latter. Other studies^36,37 show that the main type of crude oil exported from Russia to the European Union is Urals. We therefore assume that Other Russian Crude Oil comprises of 70% Urals and 30% Siberian Light Sweet crude oil — the two types’ shares in Russian production. This may be considered a conservative approach. Our results remain qualitatively unchanged without this assumption.