Introduction

The stage where a planet’s silicate interior is completely or partially molten during early differentiation (so-called magma ocean) is crucial in defining the chemical structure of rocky planets within the solar system1,2, and those in extrasolar systems3. To gain a deeper understanding of the depth, dynamics, and duration of the magma ocean, it is imperative to determine the physical properties and atomic structure of liquid silicates over the whole range of temperature and pressure conditions encountered in planetary mantles. On Earth, pressure reaches up to 136 GPa at the base of the rocky mantle. The recent discovery of Super Earths—exoplanets exhibiting densities consistent with rocky interiors and radii up to 1.8 times that of Earth4 —requires expansion of the current investigation of molten silicates over a wider pressure range. Examining the influence of elevated pressure and temperature conditions on the local structure of liquid silicates provides a unique opportunity to glean insights into the effects of size and mass on early planetary differentiation processes. By understanding these complex relationships, we can unlock valuable insights into the diverse nature of exoplanets.

Despite the importance of understanding the atomic scale structure of silicate liquids at high pressures, such measurements are challenging using static compression techniques. For example, the complexity of multi-anvil presses experiments above 30 GPa and 3000 K limits the application of method for studying liquid silicates at the pressure conditions relevant to the deep interiors of Earth and super-Earths5. To extend the range of pressures explored, laser-heated diamond-anvil cells (DACs) combined with synchrotron X-ray diffraction have been used in recent years to determine silicate melting temperatures6,7,8,9. However, due to a range of issues including limited reciprocal space coverage, severe background contribution from the diamond anvils, and strong thermal gradients, no study has been able to determine the atomic-scale structure of silicate liquids at the relevant pressures to inform Earth and super-Earth exoplanets’ interiors. In our previous study, we have combined high-brilliance X-ray beams from an X-ray free electron laser (XFEL) with high-power lasers at nanosecond timescales, to conduct in situ XRD investigations of shock-compressed liquids and glasses, highlighting qualitative similarities with the XRD patterns of glasses compressed at ambient temperature10. However, those experiments did not provide sufficient coverage in reciprocal (Q) space (up to 50 nm−1) to directly assess the atomic structure of the silicate melts and glasses, thus hindering quantitative comparison. The recent developments at the LCLS provide now higher X-ray energies (17 keV in the present study), combined with the large angle coverage and the low background signal from the recently installed ePix 10 K detectors, has expanded the experimental capabilities, enabling the collection of diffuse scattering over a large enough Q-range (15–105 nm−1) (Fig. 1). Increasing the Q range from 50 to 105 nm−1 allows for the Fourier transform of the diffuse scattering, and therefore to quantitatively determine the atomic structure in real space through the pair distribution function, g(r). With these developments, we provide the first in situ study of the atomic-scale structure of liquid silicate at unprecedented pressure-temperature (P-T) conditions relevant for deep magma oceans of Earth and super-Earth exoplanets, i.e., up to 385(40) GPa over 18,000 K.

Fig. 1: Schematic illustration of the experimental set up available at MEC end-station.
figure 1

The four epiX 10k detectors are covering a Q-range between 15 and 106 nm−1, for an X-ray beam energy of 17 keV. The diffuse scattering recorded on each detector can be then stitched to reconstruct the full signal (Fig. S2).

Full size image

Here, we present experimental results on the structural investigation of laser-shocked (Mg,Fe)SiO3 glasses performed at the MEC end-station of LCLS and a comparison with ab initio molecular dynamics calculations under similar thermodynamic conditions. Our dataset probes a large range of Fe content (up to 0.2 for the X(Fe) / [X(Fe) + X(Mg)] ratio) and of pressure along the Hugoniot (from 80 to 385 GPa), greatly expanding previous investigations that had been limited up to 60 GPa11. These comparisons allow us to understand the densification mechanism up to densities relevant for deep magma oceans of super Earths. Indeed, 385 GPa would correspond to the core-mantle boundary of super-Earths with ~3 times the mass of the Earth12.

Results

The use of the short duration/high brightness XFEL pulse probe allowed us to acquire high-quality diffuse scattering data from shock-compressed liquid silicates, providing appropriate signal-to-noise ratio to perform structural analysis on data from a single pulse acquisition (~60 fs). The use of the high-power laser driver at the MEC instrument enabled us to shock compress the samples up to hundreds of GPa and several thousands of K (18,000 K at the highest probed pressure) conditions over a few nanoseconds; data acquisition was thus performed on timescales shorter than those of chemical diffusion, avoiding potential migration and changes in stoichiometry. The thermodynamic P-T conditions reached during the shock were assessed using interferometric measurements and reformulated equation of state data (details in the Methods section).

The high quality of the diffuse scattering data obtained by combining the LCLS X-ray source and high-power laser at MEC end-station is apparent in Fig. 2, which shows the normalized X-ray structure factor (SX(Q)) (the X superscript stands for X-ray data, to distinguish from non-X-ray weighted ab initio data) alongside the corresponding radial distribution function gX(r) for a series of representative shock-compressed (Mg0.95Fe0.05)SiO3 liquids up to ~350 GPa.

Fig. 2: Experimental dataset of liquid (Mg0.95Fe0.05)SiO3 along the Hugoniot.
figure 2

a X-ray weighted structure factors SX(Q) after normalization. b Inferred radial distribution function gX(r). Pressure and density were determined from VISAR measurements (see Methods). Analysis was performed using the Amorpheus software13 (see Methods).

Full size image

The calculation of SX(Q) and gX(r) from Ab Initio Molecular Dynamics (AIMD) calculations provides valuable insights to analyze and interpret the experimentally obtained total scattering. Indeed, each peak in the SX(Q) results from the combined complex contributions of each atomic pair, possibly positive or negative (Fig. 3, left panel). The first peak at Q ~ 28.5 nm−1 results from the positive contribution of the cation-cation pairs together with the O-O bonds. The second peak at Q ~ 38 nm−1 is mainly due to O-O and Mg-O bonds, with an increasing contribution of Si-O at larger Q values. In the X-ray weighted total radial distribution gX(r) function (Fig. 3, right panel), the first coordination sphere, denoted as r1, primarily encompasses the shortest bonds such as Si-O and Mg-O. On the other hand, the second coordination sphere, referred to as r2, predominantly represents the O-O bond distance, together with small contributions from cation-cation pairs, mainly Mg-Si bond.

Fig. 3: AIMD calculations on MgSiO3 glass Hugoniot at 6000 K (P = 167 GPa; density of 5.17 g/cm3).
figure 3

a Total and partial X-ray weighted (see Methods and Figure S7) structure factors SX(Q). b Total and partial X-ray weighted (see Methods and Figure S6) radial distribution functions gX(r).

Full size image

Our experimental data does not exhibit any significant trend or structural difference due to changes in Fe content (Fig. S5). This is further supported by comparison of AIMD calculations of the structure factors and radial distribution functions between pure MgSiO3 and in a composition close to (Mg0.9Fe0.1)SiO3 (Fig. S9) at similar conditions. Thus, given the relatively low Fe contents and the overall weak contribution to the local structure, our approach comparing our Fe-bearing experimental results with AIMD calculations on pure MgSiO3, cold compression of MgSiO3 glass14 is suitable.

In our previous study10, we demonstrated that, at comparable densities, there are significant similarities in the diffractogram of high-temperature glasses and liquids, as well as cold compressed glasses, in particular the diffuse diffraction peak positions. However, the limited Q-range prevented us from investigating the local structure gX(r) and determining whether the features observed in reciprocal space have comparable signatures and similarities in real space. In this study, thanks to the availability of high-energy XFEL radiation at 17 keV, we can analyze the structural properties of MgSiO3 glass shock-compressed along the Hugoniot, and provide a direct and quantitative comparison with previously published local structure data obtained at comparable densities14 (Fig. 4). Furthermore, the comparison with AIMD simulations enables us to deconvolute the contributions from different atomic pairs, providing a detailed view of the local atomic structure.

Fig. 4: Direct comparison between DFT-MD calculations (dashed curves) and experimental results (solid curves) for shock compressed (Mg,Fe)SiO3 at similar conditions (thermodynamic conditions are indicated).
figure 4

a Structure factors SX(Q). b Radial distribution function gX(r).

Full size image

The AIMD-derived total gX(r) is obtained by summing the partial gX(r) following the formalism presented in ref. 15; the result is directly comparable to our experimental data, and it exhibits good agreement, capturing well the overall shape and the peak position (Fig. 4, right panel). The main difference between experiments and calculations is the shape of the first and second coordination spheres. This is an expected effect due to the limited experimental Q range, which affects the height and width of the peaks, but not their position15. In addition to the comparison in real space, partial structure factors could be calculated (see Methods) to derive X-ray weighted Density Functional Theory-Molecular Dynamics (DFT-MD) total SX(Q) to be compared with our experimental results (Fig. 4, left panel).

Dynamic compression anchors the sample’s P-T conditions along the Hugoniot curve. In order to compare the structure of liquid silicates over this wide pressure and temperature range, we find that using density (ρ) provides straightforward comparison10; indeed ρ variations control the local volume and, therefore the bond distances. Here, our results are collected along the Hugoniot, from 4.58(09) g/cm3 (at 81(9) GPa) up to 6.01(12) g/cm3 (385(40) GPa), as determined from VISAR interferometric measurements.

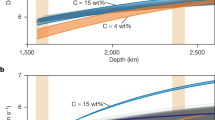
In order to interpret our dataset, positions of the maximum of the two first oscillations of the gX(r), i.e., r1 and r2, are plotted as a function of ρ (Fig. 5). We observe only a small shift of the first peak (from 0.17 to 0.175 nm) while the second peak exhibits a more marked shift toward lower r values at increasing density (from 0.22 to 0.25). For both peaks, we report an overall agreement between experimental data extracted from XRD and our AIMD calculations (Fig. 5).

Fig. 5
figure 5

Peak positions (r1 and r2) of total gX(r) from shock-compressed MgSiO3 liquids compared with cold compressed MgSiO3 glasses (and associated error bars)14 and DFT-MD (Supplementary Data 2), as a function of density and temperature (See Methods). r1 and r2 refer to the two first peaks of the total gX(r). Star symbols represent AIMD simulations performed on the Hugoniot P-T-ρ conditions for MgSiO3 glass starting material.

Full size image

Utilizing the Hugoniot P-T-ρ relation computed in the present study (see Methods), temperature estimations can be derived for each shot, as outlined in Supplementary Data 1. Upon examining the first peak (r1), a slight increase with increasing density and increasing temperature along the Hugoniot path could be seen (Fig. 5, top), with an excellent agreement between theory and experiment. For the second peak (r2), the experimental findings align remarkably well with the temperature trend derived from ab initio MD, with decreasing trends with increasing density and increasing temperature, provoking a merging with r1 above 8000 K (Fig. 5, bottom).

Discussion

During shock compression, each sample reaches a specific state of pressure, density, and temperature that lies along the Hugoniot curve of the material, which complicates the disentanglement of temperature and pressure effects in our dataset. Consequently, the most effective approach to compare laser-driven shock compression at extreme temperatures up to 10,000 K with cold compressed glass at 300 K is to directly compare the changes in the local structures as a function of density. The analogy should be thus drawn at similar densities rather than similar pressures, as high-pressure states along the Hugoniot are necessarily affected by temperature effects. For instance, structural features observed in a cold compressed MgSiO3 glass at 80 GPa should be compared with the liquid’s structural organization at 135 GPa and 4000 K, representing conditions at the Earth’s core-mantle boundary.

The position of the first peak r1, associated with Si-O and Mg-O bonds, is barely modified by increasing density, highlighting the stiffness of these bonds with respect to pressure. Along isothermal paths, AIMD simulations show that r1 peaks are following a monotonic decrease with increasing density, although changes remain limited to a few % over the whole range here examined. Our experimental points, on the contrary, exhibit a slight increase along the Hugoniot P-T states. This trend is well reproduced by AIMD calculations, and it is mainly related to the rapid increase in temperature along the Hugoniot.

Contraction of O-O and Mg-Si distances with increasing pressure and temperature for liquid silicates is noticeable from the DFT-MD results (Fig. 3 and Fig. S8) and confirmed by our experimental results. A distinct shift in the gX(r) second peak, r2, becomes evident with increasing pressure and temperature, both in the experiment and in the calculations highlighting a significant contrast between shock and static compression (Fig. 5). The overall temperature dependence of the local structure is thus more significant for the O-O and Mg-Si networks (r2 peak) compared to the Si-O/Mg-O distances (r1 peak). This temperature dependence of the r2 peak at a given density underscores the limitations of the glass/liquid analogy at extreme pressure conditions.

Under ambient pressure, the importance of the O-O network in determining the material’s properties, such as glass-forming ability, has been evidenced by the differences between MgSiO3 and Mg2SiO4 liquids16. The present experimental evidence of a strong O-O contraction has thus important implications for understanding the mechanism of densification of liquid silicates17. It is interesting to note that the relative stiffness of the Si-O bond compared to the strong O-O compaction had been already highlighted in the absence of Mg and Fe, i.e., for liquid SiO2 by DFT-MD calculations made up to 500 GPa18.

Different hypotheses have been proposed to explain the liquid silicates densification processes under high pressure, for instance, structural disorder17, Si-O-Si bond angle change19, and oxygen tri-clusters increase20. For density below 5 g/cm3, Si-O bond length evolution, in correlation with coordination changes, has a strong impact on the densification process14. However, for densities up to 6 g/cm3, our experimental measurements combined with DFT-MD results demonstrate that the main factor driving the densification process is the O-O and Mg-Si bonds contraction. Hence, different mechanisms may regulate the densification processes under deep Earth and super-Earth pressure conditions, respectively.

Our data highlight the dramatic shortening of r2, by more than 30% over the density range investigated, in contrast to the slight evolution of the r1 feature. Extrapolated to higher pressure and temperature conditions, this trend could lead toward the merging of the first and the second coordination spheres under extreme pressures. This is clearly visible in DFT-MD and experimental structure under the most extreme conditions (Fig. 5). While this is in part due to the extreme temperatures that enlarge the coordination sphere, our study reveals that the main driver is likely the dramatic compression of the O-O and Mg-Si networks.

The use of in situ XRD combined with laser-driven compression directly probing silicates in their liquid state under extreme conditions offers significant potential for advancing geophysical research. Here, we report data on liquid (Mg,Fe)SiO3 at unprecedented pressures, providing information on the local structure up to 385 GPa. Interestingly, our data shows no clear evidence of MgSiO3 dissociation, a phenomenon previously reported in the liquid state21. This absence of transition bears significant implications for understanding the dynamics of large magma oceans in young Super-Earths. Furthermore, the temperature-dependent shift in peak positions highlighted in Fig. 5 underscores discernible differences in the local structure between glass and liquid phases, potentially reshaping previous assumptions regarding processes occurring in the deep Earth’s mantle14. Lastly, the observed O-O bond contraction, along with Mg-Si distance, may exert a profound influence on macroscopic properties, potentially leading to drastic implications for the dynamics of large magma ocean planets. The dramatic changes in local structure as a function of density here observed suggest that different differentiation processes may determine the evolution of rocky planets depending on their size rather despite having similar chemical compositions. This would imply a potentially different internal structure and evolution for planets like Venus and the Earth and large, “Super-Earth” exoplanets.

The development of XFEL sources combined with high-power lasers offers exciting opportunities to study in situ the local structure of shock-compressed materials under pressure and temperature conditions that are not currently achievable with static compression techniques. Here, a high-energy XFEL probe of 17 keV allows the extension of the Q range of XRD measurements to 100 nm−1, enabling the quantitative structural analysis of liquid silicates at pressures of hundreds of GPa for the first time, extending by almost one order of magnitude the pressure and temperature achieved in previous experiments11. The excellent agreement with DFT-MD calculations demonstrates the high quality of our experimental results and make now possible a detailed study of the densification mechanism, mainly dominated by the contraction of the O-O and Mg-Si networks. This study opens exciting new opportunities for studying planetary materials under magma ocean conditions for Earth and Super Earth conditions.

Methods

Target preparation

The (Mg1-xFex)SiO3 glasses used in this study were synthesized through the laser levitation method. We mixed (Mg,Fe)O and SiO2 reagents to reproduce the starting material compositions of (Mg,Fe)SiO3. Four compositions were prepared with varying iron contents (x = 0, 0.05, 0.1, 0.2). The synthesis was conducted in a reducing atmosphere buffered by a CO-CO2 gas mixture to ensure the ferrous state of Fe.

These spheres were then cut and double-face polished to approximately 50 µm. The thickness of each individual target was measured using a comparator, leading to a precision of ±1 µm for the thickness. After polishing, the front surface of the sample was coated with ~300 nm layer of Al, then glued using UV glue on 75 µm black Kapton, serving as an ablator for the shock experiments.

Laser-driven shock compression

Laser-driven shock compression experiments have been performed using the frequency-doubled Nd-glass laser beams available at the Matter in Extreme Conditions (MEC) end-station of the Linac Coherent Light Source (LCLS) at SLAC National Accelerator Laboratory. We produced Hugoniot states inside the sample by using flat-top temporal pulses of 8 ns with focal spots of 150 and 300 µm diameter on target using continuous phase plates available at MEC. The delay between the drive laser and the X-ray pulse was chosen to ensure homogeneous P-T conditions inside the shocked area probed with X-ray pulses. For our target design, this condition is met up to a maximum shock front propagation distance of ~40 μm inside the sample and before the shock front breaks out from the sample.

The hydrodynamics was monitored using two velocity interferometry systems for any reflector (VISAR) operating at 532 nm. For typical targets, without a rear window, VISAR images provide the transit time of the shock inside the sample and eventually its free surface velocity. Some targets had a LiF window, so that VISAR measured the apparent velocity of the sample/LiF interface. From the known properties of shocked LiF22 and by impedance matching with MgSiO3 glass Hugoniot, this measurement allows us for the determination of the sample pressure at its interface with the LiF.

1D hydrodynamic simulations with the MULTI code have been used to design the target assembly (75 µm black kapton/0.3 µm Al coating/50 µm target) and optimize the uniformity of shock compression. The thickness of the Kapton layer played a crucial role in maintaining shock stationarity within the MgSiO3 glass, extending up to 40-45 µm depths, as evidenced in Fig. S1, which presents time sequences of the shock pressure within the silicate layer. As the X-rays probe the bulk target, the timing of the X-ray pulses was set at 0.5−1 ns prior to shock breakout. This choice guarantees contributions from uniformly shocked samples, ensuring the reliability of the XRD patterns.

MgSiO3 glass Hugoniot has been investigated by both gas-gun23,24,25,26 and laser-driven10,21,27 shock compression experiments as well as ab initio molecular dynamics simulations (AIMD)28. While both experimental and DFT-MD data agree in the pressure range covered by gas-gun experiments (up to 160 GPa), discrepancies exist above 450 GPa between existing AIMD and laser-driven shock experiments from Spaulding et al.21. On one hand, these laser-shock experiments on MgSiO3 glass21 have not been reproduced by decaying shock experiments27. On the other hand, the AIMD Hugoniot from Militzer28 assumes the internal energy of the glass at ambient conditions to be equal to the one of crystalline enstatite. (see AIMD section below). For these reasons, we constructed a Hugoniot relation for MgSiO3 glass considering both previous gas-gun measurements and AIMD Hugoniot data from the present study. We performed a linear fit using the following formulation:

$${U}_{s}=S{U}_{p}+{C}_{0}$$
(1)

where \({U}_{s}\) and \({U}_{p}\) are the shock front and fluid velocities, respectively, and \(S=1.4712\) and \({C}_{0}=3.5084\) km/s with the following covariance parameters:

$${\sigma }_{{SS}}^{2}=2.560\times {10}^{-4},{\sigma }_{{C}_{0}{C}_{0}}^{2}=5.069\times {10}^{-3},{\sigma }_{S{C}_{0}}=-1.026\times {10}^{-3}$$
(2)

We consider a similar hydrodynamic behavior between pure and Fe-bearing (Mg,Fe)SiO3 glasses, i.e., the relation between Us and Up remains valid for all the compositions investigated here. This assumption is acceptable given the low Fe concentrations investigated here. It can be further supported as existing gas-gun Hugoniot data included in the fit have samples with initial densities between 2.76 and 2.83 g/cm3, similar to glasses with Fe content up to (Mg0.9,Fe0.1)SiO3, without apparent influence on the Us-Up trend. The initial density of the glass is considered when calculating the pressure (\({P=\rho }_{0}{U}_{s}{U}_{p}\)) and the density (\({\rho=\rho }_{0}{U}_{s}/({U}_{s}-{U}_{p})\)) of shocked state. The initial densities of the different compositions are provided in Supplementary Data 1.

X-ray diffraction (XRD) analysis

The incident X-ray probe was set at an energy of 17 keV, with a pulse duration of ~60 fs and focused down to a size of 30 µm of diameter FWHM. X-ray diffraction signal was recorded using four ePix 10k detectors. The standard configuration with these detectors covers an angular range between 8 and 72 two theta degrees, resulting in an XRD pattern with an exploitable Q-range of 15–105 nm−1 (Fig. 1). An example of a stitched pattern combining signals from all four detectors is given in Fig. S2.

As the probe time is adjusted before the shock breakout of the target, an XRD pattern contains a contribution from both ambient condition glass and a hot shock-compressed liquid. The removal of the contribution from the cold glassy part is performed using the patterns measured before the shock (Fig. S3). The percentage of cold contribution is first fixed following VISAR timing and then adjusted to obtain a continuous low Q range on the shocked signal. The diffuse scattering from the undriven glass is markedly different from the high-pressure one, with a strong contribution at low Q. This difference allows for finely tuning the fraction of unshocked glass to be subtracted from the XRD pattern and avoid artifacts in the low Q-range of the shocked liquid patterns.

The corrected diffraction patterns for shocked liquid are then analyzed using the Amorpheus Python code13. This software allows for the extraction of the density of liquid using the minimization at a low distance on the obtained X-ray weighted radial distribution function gX(r)29,30. The global analysis is performed after 5 iterations, for the removal of the noise at low r. Final gX(r) is obtained by applying a Lorch modification function13. The obtained data are presented in Fig. 2.

Our research, enabled by the use of XFEL technology, has been at the forefront of extracting density values from XRD analysis of liquid materials under high pressure, complementing our study of the local structure. The methodology previously employed for laser-heated diamond-anvil cell experiments or large volume press30 has been successfully applied to laser-driven shock datasets. Since the probing time ensured that the thermodynamic conditions are on the Hugoniot, the density obtained from the analysis using the Amorpheus software could be directly compared with VISAR measurements and the density derived from the Hugoniot P-ρ relation (Fig. S4).

Despite the relatively large error bars, a reasonable agreement between VISAR and Amorpheus densities (Fig. S4) is observed up to a density of 5.8 g/cm3. However, beyond this point, the density extracted from Amorpheus appeared to plateau, while the VISAR density continued to increase. This discrepancy might be attributed to the observed structural changes, as the different features of SX(Q) shifted towards higher Q ranges with increasing density. Achieving a more refined density estimation may necessitate an expansion of the Q range at higher densities. The acquisition of density information through structural refinement in the liquid state holds significant importance for future measurements of liquid properties off the Hugoniot, such as release or double shock experiments31.

Ab initio Molecular Dynamics (AIMD) calculations

MgSiO3 liquid was investigated by AIMD simulations within the Born-Oppenheimer approximation as implemented in the plane-wave code VASP v5.232,33. For a given configuration of the Mg, Si and O pseudo-nuclei, the electronic ground state is calculated from finite-temperature density functional theory (DFT) using Mg (8 valence electrons), Si (4 valence electrons) and O (6 valence electrons) standard projected augmented wave pseudopotentials. The resulting forces are used to compute the dynamics of the system in a classical framework. We employed the Perdew-Burke-Ernzerhof (PBE) exchange-correlation functional34 used a cut-off of 700 eV for the plane wave basis set expansion and sampled the Brillouin zone at the Gamma-point. We simulated the evolution of a cubic supercell containing 160 atoms in a NVT ensemble with a time step of 0.5 fs or 1 fs and a temperature controlled by velocity scaling (isokinetic ensemble). At least 4000 steps were dedicated to thermal equilibration of the system and more than 20,000–60,000 steps were used for statistics and trajectory processing.

We sampled more than 45 different volume-temperature conditions along four different isotherms at 4000, 6000, 8000, and 15000 K (Supplementary Data 2). The initial MgSiO3 liquid configuration was produced by melting a 1x1x2 supercell of enstatite at 6000 K using LAMMPS using Oganov potentials35 first in NVT and then NPT ensembles to obtain a cubic supercell at around 40 GPa. This structure was then equilibrated using VASP at 6000 K and served as a starting configuration for all DFT-MD performed at 6000 K. For each volume, the last configuration obtained at 6000 K served as the starting configuration at 4000 K, 8000 K, and 15000 K.

The Hugoniot of MgSiO3 glass is determined by finding the pressure-volume (P-V) conditions which validate the following equation along each isotherm:

$$E-{E}_{0}+\frac{1}{2}\left(V-{V}_{0}\right)\left(P+{P}_{0}\right)=0$$
(3)

This calculation requires the knowledge of the initial volume (V0) or density (ρ0) and internal energy (E0) of the undriven MgSiO3 glass. Obtaining this value in the ambient temperature glass requires a good structural equilibration, which is not straightforward due to the limited time and spatial scales accessible with AIMD. To avoid this issue, Militzer28 assumed that the internal energy of ambient MgSiO3 enstatite crystal is close to the one of the glass. In the present study, we calculate E0 of the glass at 300 K by first equilibrating a liquid at 4000 K and at the ambient conditions density (2.74 g/cm3) and then by ‘slowly’ quenching it down to 300 K at a rate of ~0.3 K/fs. Such high-temperature structural equilibration and quench procedure have been proven to provide the best comparison between computed and experimental glasses36. We obtain a final pressure of 0.5 GPa at 300 K and 2.74 g/cm3. At both 300 K and 4000 K (better configurational statistics), structure factors compare well with experimental data at ambient density. This agreement suggests that the corresponding E0 of MgSiO3 glass at 300 K (−34.5336 kJ/g) is reliable. We note that using the E0 of MgSiO3 glass instead of using the E0 of crystalline enstatite (as done in ref. 16) results in a ~4–5 GPa difference in the computed Hugoniot pressures.

DFT-MD partial static structure factors \({{{{\rm{S}}}}}_{{{{\rm{\alpha }}}}{{{\rm{\beta }}}}}({{{\rm{Q}}}})\) are directly calculated from the atomic positions \({{{{\rm{r}}}}}_{{{{\rm{i}}}}}\) using the library Dynasor (https://dynasor.materialsmodeling.org/) and considering an isotropic system as follows:

$${{{{\rm{S}}}}}_{{{{\rm{\alpha }}}}{{{\rm{\beta }}}}}({{{\rm{Q}}}})=\frac{1}{\sqrt{{{{{\rm{N}}}}}_{{{{\rm{\alpha }}}}}{{{{\rm{N}}}}}_{{{{\rm{\beta }}}}}}}{\sum}_{{{{\rm{i}}}}}^{{{{{\rm{N}}}}}_{{{{\rm{\alpha }}}}}}{\sum}_{{{{\rm{j}}}}}^{{{{{\rm{N}}}}}_{{{{\rm{\beta }}}}}}\left\langle {{{{{\rm{e}}}}}^{{{{\rm{iQ}}}}\cdot {{{{\rm{r}}}}}_{{{{\rm{i}}}}}}{{{\rm{e}}}}}^{-{{{\rm{iQ}}}}\cdot {{{{\rm{r}}}}}_{{{{\rm{j}}}}}}\right\rangle$$
(4)

where \( < > \) denotes the ensemble average and \({{{{\rm{N}}}}}_{{{{\rm{\alpha }}}}}\) the number of atoms of species \({{{\rm{\alpha }}}}\). Ashcroft-Langreth partial structure factors \({{{{\rm{S}}}}}_{{{{\rm{\alpha }}}}{{{\rm{\beta }}}}}^{{{{\rm{AL}}}}}({{{\rm{Q}}}})\) are then obtained from \({{{{\rm{S}}}}}_{{{{\rm{\alpha }}}}{{{\rm{\beta }}}}}({{{\rm{Q}}}})\) by:

$${{{{\rm{S}}}}}_{{{{\rm{\alpha }}}}{{{\rm{\beta }}}}}^{{{{\rm{AL}}}}}({{{\rm{Q}}}})=\frac{1}{\sqrt{{{{{\rm{c}}}}}_{{{{\rm{\alpha }}}}}{{{{\rm{c}}}}}_{{{{\rm{\beta }}}}}}}{{{{\rm{S}}}}}_{{{{\rm{\alpha }}}}{{{\rm{\beta }}}}}({{{\rm{Q}}}})$$
(5)

where \({{{{\rm{c}}}}}_{{{{\rm{\alpha }}}}}={{{{\rm{N}}}}}_{{{{\rm{\alpha }}}}}/{\sum}_{{{{\rm{k}}}}}{{{{\rm{N}}}}}_{{{{\rm{k}}}}}\). From the set of \({{{{\rm{S}}}}}_{{{{\rm{\alpha }}}}{{{\rm{\beta }}}}}^{{{{\rm{AL}}}}}({{{\rm{Q}}}})\), the X-ray weighted total structure factor (Fig. 4) is given by:

$${{{{\rm{S}}}}}_{{{{\rm{tot}}}}}^{{{{\rm{X}}}}}({{{\rm{Q}}}})={\sum}_{{{{\rm{\alpha }}}}}{\sum}_{{{{\rm{\beta }}}}}{{{{\rm{f}}}}}_{{{{\rm{\alpha }}}}}({{{\rm{Q}}}}){{{{\rm{f}}}}}_{{{{\rm{\beta }}}}}({{{\rm{Q}}}})\sqrt{{{{{\rm{c}}}}}_{{{{\rm{\alpha }}}}}{{{{\rm{c}}}}}_{{{{\rm{\beta }}}}}}{{{{\rm{S}}}}}_{{{{\rm{\alpha }}}}{{{\rm{\beta }}}}}^{{{{\rm{AL}}}}}({{{\rm{Q}}}})/{\sum}_{{{{\rm{k}}}}}{{{{\rm{c}}}}}_{{{{\rm{k}}}}}{{{{\rm{f}}}}}_{{{{\rm{k}}}}}^{2}({{{\rm{Q}}}})$$
(6)

with \({{{{\rm{f}}}}}_{{{{\rm{\alpha }}}}}({{{\rm{Q}}}})\) the atomic X-ray elastic scattering factors are taken from Waasmaier and Kirfel, Acta Cryst. A51, 416-431 (1995)37.

Following this, we defined X-ray weighted partial structure factors \({{{{\rm{S}}}}}_{{{{\rm{\alpha }}}}{{{\rm{\beta }}}}}^{{{{\rm{X}}}}}({{{\rm{Q}}}})\):

$${{{{\rm{S}}}}}_{{{{\rm{\alpha }}}}{{{\rm{\beta }}}}}^{{{{\rm{X}}}}}({{{\rm{Q}}}})=(2-{{{{\rm{\delta }}}}}_{{{{\rm{\alpha }}}}{{{\rm{\beta }}}}}){{{{\rm{f}}}}}_{{{{\rm{\alpha }}}}}({{{\rm{Q}}}}){{{{\rm{f}}}}}_{{{{\rm{\beta }}}}}({{{\rm{Q}}}})\sqrt{{{{{\rm{c}}}}}_{{{{\rm{\alpha }}}}}{{{{\rm{c}}}}}_{{{{\rm{\beta }}}}}}{{{{\rm{S}}}}}_{{{{\rm{\alpha }}}}{{{\rm{\beta }}}}}^{{{{\rm{AL}}}}}({{{\rm{Q}}}})/{\sum}_{{{{\rm{k}}}}}{{{{\rm{c}}}}}_{{{{\rm{k}}}}}{{{{\rm{f}}}}}_{{{{\rm{k}}}}}^{2}({{{\rm{Q}}}})$$
(7)

such that the summation of the X-ray weighted partial structure factors equals the X-ray weighted total structure factor.

The pair radial distribution functions are X-ray weighted according to the Warren-Krutter-Morningstar approximation38,39:

$${{{{\rm{g}}}}}_{{{{\rm{\alpha }}}}{{{\rm{\beta }}}}}^{{{{\rm{X}}}}}({{{\rm{r}}}})={{{{\rm{c}}}}}_{{{{\rm{\alpha }}}}}{{{{\rm{c}}}}}_{{{{\rm{\beta }}}}}{{{{\rm{f}}}}}_{{{{\rm{\alpha }}}}}({{{\rm{Q}}}}=0){{{{\rm{f}}}}}_{{{{\rm{\beta }}}}}({{{\rm{Q}}}}=0)/{\left({\sum}_{{{{\rm{k}}}}}{{{{\rm{c}}}}}_{{{{\rm{k}}}}}{{{{\rm{f}}}}}_{{{{\rm{k}}}}}({{{\rm{Q}}}}=0)\right)}^{2}$$
(8)

and the X-ray weighted total PDF is obtained by:

$${{{{\rm{g}}}}}^{{{{\rm{X}}}}}({{{\rm{r}}}})={\sum}_{{{{\rm{\alpha }}}}}{\sum}_{{{{\rm{\beta }}}}}{{{{\rm{g}}}}}_{{{{\rm{\alpha }}}}{{{\rm{\beta }}}}}^{{{{\rm{X}}}}}({{{\rm{r}}}})$$
(9)

An example of the comparison between X-ray weighted and non X-ray weighted data is presented in Figs. S6 and S7. For each DFT-MD, the corresponding comparison is provided in the Supplementary Dataset.