Rapid context inference in a thalamocortical model using recurrent neural networks

Abstract

Cognitive flexibility is a fundamental ability that enables humans and animals to exhibit appropriate behaviors in various contexts. The thalamocortical interactions between the prefrontal cortex (PFC) and the mediodorsal thalamus (MD) have been identified as crucial for inferring temporal context, a critical component of cognitive flexibility. However, the neural mechanism responsible for context inference remains unknown. To address this issue, we propose a PFC-MD neural circuit model that utilizes a Hebbian plasticity rule to support rapid, online context inference. Specifically, the model MD thalamus can infer temporal contexts from prefrontal inputs within a few trials. This is achieved through the use of PFC-to-MD synaptic plasticity with pre-synaptic traces and adaptive thresholding, along with winner-take-all normalization in the MD. Furthermore, our model thalamus gates context-irrelevant neurons in the PFC, thus facilitating continual learning. We evaluate our model performance by having it sequentially learn various cognitive tasks. Incorporating an MD-like component alleviates catastrophic forgetting of previously learned contexts and demonstrates the transfer of knowledge to future contexts. Our work provides insight into how biological properties of thalamocortical circuits can be leveraged to achieve rapid context inference and continual learning.

Introduction

Context is an abstract collection of goals, memories and external cues that inform appropriate behavioral responses^1,2. Humans and animals exhibit flexible decision-making based on changing contexts. This flexibility is demonstrated by the ability to generate context-dependent learned actions and to adapt quickly and flexibly to new contexts without overwriting previous learning. To accomplish these goals, context inference is an essential process that underlies many aspects of cognitive flexibility. Empirical evidence from studies in both humans and animals highlights the importance and benefits of context inference^3,4,5,6,7. Impaired context inference has been associated with reduced cognitive flexibility and several mental disorders, such as schizophrenia^8,9.

The neural mechanisms underlying context inference are still under investigation using different techniques, e.g., neurophysiological measurements and computational theories. It has long been known that the prefrontal cortex (PFC) plays a critical role in cognitive flexibility^1,10. The PFC receives many inputs from and sends outputs to other brain regions, including the cortex, thalamus, and amygdala. Among these regions, the mediodorsal thalamus (MD) has received particular attention recently due to its dense projections to the PFC^11,12. Recent studies have demonstrated that MD regulates PFC dynamics and effective connectivity in the service of adaptive behaviors^{4,13,14,15,16,17,18,19,20}. Specifically, the MD amplifies local cortical connectivity and sustains rule representations in the PFC^13,21,22. The MD encodes cueing contexts (the statistical regularity of cue presentation) and regulates the PFC responses. In this way, the MD sustains context-relevant PFC representations while suppressing the context-irrelevant ones⁴. Behavioural performance in mice suggests that context inference can occur rapidly within just a few trials. In addition to its role in context inference, the MD has been implicated in a range of other cognitive functions^12,23,24,25. These findings underscore the critical role of thalamocortical interactions in inferring temporal context, a key component of cognitive flexibility⁶.

In recent years, recurrent neural networks (RNN) have been widely used for computational modeling of prefrontal cortex (PFC) dynamics^3,26,27. Although neural networks have shown good performance in various cognitive tasks^28,29, they usually suffer from severe performance degradation on previously learned tasks when tasks are learned sequentially, which is referred to as catastrophic forgetting. The whole neural networks are re-trained with new tasks without protecting prior learned knowledge of past tasks (Fig. 1B). Continual learning or lifelong learning is essential in human learning in dynamic environments and enables models to solve different tasks simultaneously without interference^30,31,32. Many continual learning approaches have been proposed and could mainly be categorized into three strategies: replay-based methods, regularization-based methods, and architecture-based methods^{33,34,35,36,37,38}, e.g., architecture-based methods utilize masking strategies to construct modular structures and regularization-based methods use task inference to have separate critical parameters across tasks. However, most continual learning methods require explicit task identifications during training, e.g., one-hot encoding vector of task identification is provided to model as well as inputs during training³. It is unclear how temporal task or context identification can be quickly and accurately inferred from neural representations while performing tasks. Here we show that incorporating biological properties of thalamocortical circuits into neural networks can help the networks infer temporal contexts continuously within a few trials and achieve continual learning in dynamically changing environments.

Fig. 1: The PFC-MD model framework with the synaptic plasticity.

A A cortico-thalamic neural network model with a Hebbian learning rule in the PFC-to-MD connections to infer temporal context and MD gating in the PFC. B The challenge in continual learning. Standard artificial neural networks modeling one brain region are optimized on single contexts and suffer from catastrophic forgetting. The learned critical model parameters of old contexts are changed in new contexts. The right arrows denote the learning process with context switch. C We propose a synaptic plasticity with pre-synaptic and post-synaptic traces, adaptive thresholding, and winner-take-all in the MD to make the neural network infer temporal contexts and enable continual learning.

To develop a rapid and online computational model of context inference, we present a novel two-system recurrent neural network model comprising an MD thalamus module and a PFC module in this work. Our model used Hebbian learning-based synaptic plasticity between the PFC and the MD in an unsupervised way, enabling the MD module to infer temporal contexts by integrating context-relevant activities over trials. The task representations of the PFC were gated by the MD projections to avoid interference between different task representations. We trained the network to perform a classification task, which was analogous to the attention-guided behavioral task that mice were trained to do. Neural recordings from the PFC and the MD of mice performing the task were consistent with the neural network. We found that the PFC-MD network outperformed a PFC-only model in being able to flexibly switch between temporal contexts. We also evaluated the model performance on more general cognitive tasks learned sequentially and compared the model performance with existing biologically plausible continual learning methods. The results demonstrated the computational advantages of the PFC-MD network in both continual learning and knowledge transfer. Our work provides insight into how biological properties of thalamocortical circuits can be leveraged to achieve rapid context inference and continual learning.

Results

The MD thalamus infers temporal context from the PFC unsupervisedly with synaptic plasticity

Our first objective is to build a simplified cortico-thalamic network model that enables the rapid inference of temporal context in the thalamus using Hebbian plasticity. This model is inspired by previous studies in mice that demonstrated selective context coding in the MD thalamus⁴. Our model comprises two critical components: (1) a Hebbian learning rule in the connections from the PFC to the MD that allows the MD to infer temporal context, and (2) the MD-to-PFC inputs that gate the activities in the PFC.

We begin by empirically demonstrating that our proposed plasticity rule allows for the robust and rapid inference of context in the MD thalamus. In subsequent sections, we will delve deeper into the details of this plasticity rule. To test the ability of our model thalamus to encode contexts, we use a context-dependent cognitive task that has been used in mice by Rikhye and colleagues⁴. In an attention-guided behavioral task, mice were presented with different cue sets corresponding to visual or auditory targets, with each cue set representing a distinct cueing context (Fig. 2A). Each cue corresponded to a specific rule, namely, attend to audition or attend to vision. The experimental results demonstrated that while the PFC neurons exhibited mixed selectivity, with some neurons responding to specific cues (cue selective) and others responding to rules regardless of cues (cue invariant), the MD neurons selectively encoded cueing context. One promising hypothesis is that the MD neurons obtain context selectivity by pooling context-specific cue inputs from the PFC and suppress the context-irrelevant PFC activities⁴.

Fig. 2: Selective encoding of temporal context in a PFC-MD model.

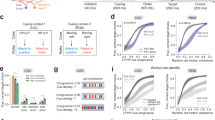
A An attention-guided behavioral task with two cueing contexts presented in blocks. B Neural networks are trained in similar alternating blocks. Cues 1 and 2 are used in context 1, while cues 3 and 4 used in context 2. Block 3 returns to context 1 to evaluate the model performance in continual learning. C The PFC and the MD neuronal activities in one single early trial of context 1 and context 2. D Decoding context (left) and rule (right) in model PFC (red) and MD (blue). MD contains information about the current context, but not the current rule (cue). Shaded area: cue period. E The decoding performance of context (brown) and rule (green) in the MD with varying numbers of cycles during training. Each cycle consists of two trials of cue 1 and cue 2 during context 1 and two trials of cue 3 and cue 4 during context 2, in random order within each cycle. The MD selectively encodes temporal contexts within a few trials. Shaded areas denote the standard deviations. F There are different clusters in the t-SNE maps of the PFC and the MD neuronal activities. Both rule and context can be decoded from the PFC while only context can be decoded from the MD. Red and blue colors denote different rules while green and orange colors represent different contexts, respectively.

We examine our neural network using a similar task design, as illustrated in Fig. 2B. Each context consists of two cue inputs, and on each trial, only one cue is input to the neural network. Figure 1A illustrates the model framework. The input is the cue sequence while the output of the network is to predict the corresponding rule given the cue input via supervised learning. We use a recurrent neural network to model the PFC and input of the PFC consists of cue input, recurrent input, and MD gating. The MD module is a feed-forward network which aims to infer the temporal context from the PFC via unsupervised learning. We consider a scenario where the network encounters a series of contexts. Standard artificial neural networks are optimized on single contexts and suffer from catastrophic forgetting since the learned critical model parameters of old contexts are totally changed in new contexts (Fig. 1B).

We propose a synaptic plasticity between the PFC and the MD to make the neural network infer temporal contexts and enable continual learning (Fig. 1C). Distinct subsets of PFC neurons are more active than others in each context. The assumption is based on the previous experimental findings by Rikhye and colleagues⁴. The experimental observations showed that the PFC neurons had mixed selectivity. A subset of PFC regular spiking neurons was cue-selective, meaning that these neurons responded to specific cues, while the context signal was more readily decodable from fast-spiking neurons in the PFC. Therefore, we develop the cortico-thalamic neural network model with the assumption that there is some degree of context-specific separation in the PFC.

The challenge for the MD thalamus is to infer the current context of the PFC in an unsupervised manner. To achieve this, we propose a Hebbian learning-based synaptic plasticity between the PFC and the MD, with three components: pre-synaptic and post-synaptic traces, winner-take-all, and adaptive thresholding (Fig. 1C; see “Methods” section for details). The synaptic weights are updated using the rule

$$\Delta w(t)=\eta \left({r}_{post}^{MD}(t)-0.5\right)\otimes \left({r}_{pre}^{MD}(t)-{\theta }_{pre}(t)\right),$$

(1)

where η is the learning rate, t is the time step within each trial. ${r}_{post}^{MD}(t)$ and ${r}_{pre}^{MD}(t)$ are the post-synaptic and pre-synaptic traces, respectively, and θ_pre(t) is an adaptive threshold. This plasticity rule allows the MD to infer temporal contexts and gate the activities and dynamics of the PFC, as shown in Fig. 1A.

To extract context information, it is necessary to consider the collection of structured information over multiple trials. Therefore, instead of relying solely on instant responses, synaptic traces are used in our model to extract context information. This is because naive Hebbian learning rules are limited in their ability to infer context, due to the timescales involved^39,40. The pre-synaptic trace extracts context information by integrating the PFC activities over time, while the post-synaptic trace stabilizes the MD outputs of different trials within the same contexts. Both traces are calculated with moving averaging over neural activities within a defined time window. Although context information can be obtained via the PFC-to-MD feed-forward connection, direct context coding is distributed (population coding) and therefore not robust and efficient for the feedback regulation in the PFC dynamics. To overcome this, we introduce competition and normalization in the MD thalamus neurons through winner-take-all (WTA), which amplifies the context coding in the MD. Following WTA, only the top K MD neurons with highest membrane potential are activated, with the hyperparameter K representing the number of the MD neurons required to encode one context. We also implement adaptive thresholding to facilitate faster learning of connections between current-context PFC and corresponding MD neurons, while simultaneously slowing the forgetting of other-context pairs. This balances the potentiation and depression of the PFC-MD synaptic weights. Hebbian learning aligns the weight vector with the direction of greatest variance in the data. Therefore, another interpretation of the PFC-MD synaptic plasticity is that the MD representation is a discretized representation of the largest principal component of the time-averaged PFC activities for generality.

Consistent with the experimental findings by Rikhye and colleagues⁴, our classification results show that both rule and context information can be decoded from the PFC while only context information can be decoded from MD, as shown in Fig. 2D. Consistently in the experimental data, the MD and PFC fast spiking neurons are the most informative of the context, whereas the PFC transient neurons are most informative of the rule in the PFC-MD network. This suggests that our proposed plasticity rule between the PFC and the MD selectively enables the MD to gain context information from the PFC. The plasticity rule allows for rapid and online context inference, and the learning of temporal contexts is fast, with the MD able to infer temporal contexts in about six trials, or three training cycles (where each cycle sequentially presents all cues from the same context). Moreover, the MD is able to adapt to varying numbers of cycles within each context during training, as shown in Fig. 2E. The context information is embedded in a low-dimensional feature space in the MD. Although by design different sets of PFC neurons are activated in different contexts (as shown in Fig. 2C, top), the separation of activation by contexts is more apparent in the MD (as shown in Fig. 2C, bottom), suggesting that the MD extracts and amplifies context information that is already presented in the PFC.

After training, the synaptic plasticity strengthens the connections between context-specific PFC neurons and the corresponding MD neurons. The synaptic weights PFC  → MD and MD  → PFC are shown in Supplementary Fig. 1. In our experiments, the first consecutive 400 PFC neurons received one context input while the following 400 PFC neurons received another context. There were totally 10 MD neurons. Analysis of the learned synaptic weights between the PFC and the MD revealed that the context-specific PFC neurons have stronger connections with the corresponding subsets of the MD neurons, while these activated MD neuron subsets inhibited the context-irrelevant PFC neurons. By projecting the high-dimensional activities of the PFC and the MD neurons onto a low-dimensional neural space using the t-distributed stochastic neighbor embedding (t-SNE) algorithm (Fig. 2F), we found evidence for both context and rule coding in the PFC, and selective context coding in the MD.

The robust selective temporal context encoding of the MD thalamus

We have demonstrated that the MD component selectively encodes temporal contexts. However, context can be decoded from the PFC as well. One interesting question would be the difference in context selectivity between the PFC and the MD. In this section, we aim to show that the MD can robustly encode temporal context even when context cannot be effectively decoded from the PFC.

To test the robustness of the PFC and MD context selectivity, we introduced different levels of time-varying noise with Gaussian distributions to the inputs and the recurrent units. At low noise levels, temporal context can be decoded from both regions, while high noise levels corrupt context decoding in both regions (Fig. 3A, B). However, at intermediate noise levels, context selectivity is substantially corrupted by noise in the PFC, while it remains strong in the MD. This effect is particularly pronounced during the delay period when the cue is no longer present (Fig. 3A, B, bottom). These results indicate that the context representations in the MD are not the same as those in the PFC.

Fig. 3: Robustness comparison of the context decoding performance in the PFC and the MD when different levels of noise are introduced to PFC units or the inputs. The MD outperformed the PFC in context decoding under various noise conditions, especially in the delay period when the cue stimuli were off.

A Comparisons of the context decoding performance with varying levels of PFC noise in the cue (top) and delay (bottom) periods. Shaded areas denote the standard deviations. B Comparisons of the context decoding performance with varying levels of input noise in the cue (top) and delay (bottom) periods. Shaded areas denote the standard deviations. C, D The MD context selectivity is robust to different model hyperparameters, e.g., the number of the MD neurons, the number of contexts. The MD can selectively encode context rather than rule with different numbers of the MD neurons and contexts in the experiment setups. Shaded areas denote the standard deviations.

Additional results that support the robustness of the MD thalamus in encoding selective temporal context are presented in Supplementary Fig. 2. From the learned weights between the PFC and the MD and the decoding performance, the selective temporal context encoding of the MD is robust to different noise and input manipulations. Even with increasing input uncertainty, where multiple cues were presented simultaneously for a short time period (e.g., 20 time steps out of an 100 time-step cue period), the MD can still robustly infer temporal context.

In our PFC-MD model, every MD neuron is assigned to encode one specific context, with no overlapping neurons between different contexts. We further demonstrate that the MD context selectivity is robust to different model hyperparameters, such as the number of MD neurons (Fig. 3C) and the number of temporal contexts represented (Fig. 3D). Notably, another key parameter in both cases is the number of the MD neurons to encode one temporal context, which was used in the top K winner-take-all in the MD normalization. The parameter K should be smaller than the number of the MD neurons divided by the number of temporal contexts to ensure the MD module encodes all temporal contexts as shown in Fig. 2C.

The mechanism of the PFC-MD synaptic plasticity in inferring temporal context

To gain further insight into the proposed PFC-MD synaptic plasticity mechanism, we examined various task-related variables with the network trained on a three-context switching task across consecutive 30 trials in each block and at the end of each block. Only the activities and weight changes in the first few trials of each block were shown in Fig. 4. There were three distinct temporal contexts (Fig. 4A), each consisting of two cues. Specifically, each cue activated a non-overlapping set of 200 PFC neurons as illustrated in Fig. 1C, left. In this analysis, we assigned the first, the second, and the third 400 PFC neurons to receive Context 1 inputs (PFC_Cxt1), Context 2 inputs (PFC_Cxt2), and Context 3 inputs (PFC_Cxt3), respectively. Additionally, we assumed that there were three subsets of the MD neurons (10 MD neurons in total): MD_A, MD_B, and MD_C neurons, selectively encoding three contexts, respectively. The pre-synaptic traces enabled the plasticity rule to integrate context information over time, resulting in higher traces for the first 400 PFC neurons relative to other context-irrelevant neurons within a few trials (Fig. 4B, left panel, and Fig. 1C, middle). The activation of the MD neurons might not be stable over different trials within the same contexts, especially in the beginning of each block (Fig. 4C, left). The post-synaptic trace was calculated by averaging the MD outputs. The winner-take-all mechanism amplified the context coding in the MD, with a few randomly activated MD neurons at the start, and increasingly stable activation of the selected MD neurons with more training trials (Figs. 4C and 1C, right).

Fig. 4: How Hebbian plasticity supports context inference in MD.

A The PFC-MD model was trained in alternating blocks with three contexts. Each context consist of two cues. Three task variables of consecutive trials in block 1 and block 2 are shown: B the MD presynaptic traces, C the MD outputs and D the weight changes over time. The first column is block 1 (Context 1) and the second column is block 2 (Context 2). Suppose that there were three types of MD neurons: MD_A, MD_B, and MD_C. E In the first block, the connections between Context 1 PFC neurons and MD_A neurons were enhanced while the connections between Context 2 PFC neurons and both MD_B and MD_C were enhanced. When Context 2 was presented, MD_B and MD_C neurons were separated to encode different contexts. The dashed arrow denotes the weakened connection between neurons. F The changes of the PFC-MD synaptic weights over time during model training: synaptic weights PFC  → MD (top) and additive synaptic weights MD  → PFC (bottom). The temporal contexts were encoded sequentially in the MD as incoming contexts were presented in blocks.

The proposed mechanism of adaptive thresholding enables the PFC-MD model to learn new temporal contexts quickly while forgetting old temporal contexts relatively slowly. Adaptive thresholding is defined as ${\theta }_{pre}(t)=\frac{1}{N}{\sum }_{i}{r}_{i,pre}^{MD}(t)$, where ${r}_{i,pre}^{MD}(t)$ is the MD pre-synaptic neuron activity at time t. Adaptive thresholding balances potentiation and depression in the PFC-MD synaptic weights determined by the differences between the MD pre-synaptic traces and the average pre-synaptic activity (${r}_{pre}^{MD}(t)-{\theta }_{pre}(t)$). According to the PFC-MD synaptic plasticity ($\Delta w(t)=\eta ({r}_{post}^{MD}(t)-0.5)\otimes ({r}_{pre}^{MD}(t)-{\theta }_{pre}(t))$), the connections between the activated PFC and MD neurons were enhanced (PFC_Cxt1 → MD_A) as shown in Fig. 4D (left). Due to the thresholding in the learning rule, the connections between the rest of the PFC and MD neurons were enhanced moderately (PFC_Cxt2 → MD_B, PFC_Cxt2 → MD_C). MD_B and MD_C neurons were not separated since only one context was presented (Fig. 4E, left). In the second block (Context 2), a different subset of the PFC and the MD neurons was activated. The connections between PFC_Cxt2 and MD_B were strengthened while the connections between PFC_Cxt2 and MD_C were weakened (Fig. 4D, E, right). MD_C neurons were saved to encode future temporal contexts. Moreover, we can see that the speed of learning and forgetting was different due to the adaptive threshold used in the synaptic plasticity. Only a small subset of the PFC neurons was stably activated given one cue as an input in a specific context. The adaptive threshold was closer to most MD pre-synaptic neuronal activities. Therefore, the connections encoding current contexts (learning) were strengthened faster (larger differences between ${r}_{pre}^{MD}(t)$ and θ_pre(t)), while the connections encoding past contexts (forgetting) were weakened more slowly. Specifically, learning is faster than forgetting about context, which is essential for learning multiple contexts.

The evolution of the PFC-MD weights over time during model training is illustrated in Fig. 4F. During the first block, only Context 1 was presented. Two MD neurons had stronger connections with Context 1 neurons in the PFC. In Block 2, two more MD neurons were selected to encode Context 2, while previous context-selective MD neurons were protected. In Block 3, another subset of the MD neurons was utilized to encode Context 3 with Context 1 and Context 2 connections protected. In Block 4, the learned PFC-MD synaptic weights were further activated and enhanced. Therefore, multiple temporal contexts were encoded sequentially in the MD during the model training.

Rapid MD context inference for more general cognitive tasks

In this section, we aim to extend our previous results, which made two major simplifying assumptions. First, we assumed a relatively simple task with static cues and a simple cue-to-output mapping, requiring no complex network dynamics. Second, we assumed a reservoir network with only learned output connections, with no learning in the recurrent network. To relax both assumptions, we present the results using more complex tasks and recurrent neural networks with learned recurrent weights. Specifically, we investigate the robustness of the PFC-MD model in more complex tasks that require dynamic processing of the input and learning in the recurrent network. Our goal is to demonstrate that the proposed model can generalize to a broader range of tasks beyond those previously investigated.

We first argue that rapid context inference is particularly challenging when the model needs to infer temporal context online and learn complex cognitive tasks at the same time (Fig. 5A). The key issue is the inherent tension between the need for rapid context inference, and the variability in PFC activities, resulting from within-trial dynamics, across-trial differences, and learning. Context representations in one single RNN (i.e., PFC) are unstable due to different time scales between task learning and the PFC-MD synaptic plasticity (rapid context inference). Within a trial, different neurons are activated at different time points. While context inference is completed within a few trials, task learning requires thousands of trials to converge in complex cognitive tasks. With complex sensory dynamics, different neurons are involved in various trials even within the same context (Fig. 5A middle). Additionally, long-term task learning also gradually changes representations in the network. Because the PFC-to-MD synaptic plasticity integrates neuronal activities of context-relevant neurons within a few trials, it is inherently unable to integrate dynamical and slow-changing representations within one single PFC (Fig. 5A right). In other words, task learning and the PFC-MD synaptic plasticity could interfere with each other in the same network module. How to balance the learning speed between context inference and task learning is challenging⁴¹.

Fig. 5: MD context inference with more complex tasks and PFC learning.

A The unique challenge of rapid context inference with complex task dynamics across trials. Different sets of neurons are activated within and across trials. The trace computation can not guarantee to cover all target task neurons that are required for all possible inputs in specific tasks. B The designed network architecture with two pathways: the task learning pathway optimized with supervised learning through the PFC and the context inference pathway through the PFC-ctx to regulate the PFC neurons. C Comparison of rules decoding and cueing context decoding accuracy in the mice experiment data, measured as mutual information, in the PFC transient neurons (cue-selective and cue invariant), the PFC fast spiking neurons and the MD neurons. ***P<0.001, Bonferroni-corrected Kruskal–Wallis ANOVA. Figure 5C reproduced from Fig. 2F of Rikhye, R.V., Gilra, A. & Halassa, M.M. Thalamic regulation of switching between cortical representations enables cognitive flexibility. (https://doi.org/10.1038/s41593-018-0269-z). D The context decoding performance of different modules: the MD, the PFC-ctx, and the PFC. ***P < 0.001, **P < 0.005, Bonferroni-Corrected Rank-Sum test. E The context decoding performance of different modules: the MD, the PFC-ctx, and the PFC over time within each trial. F The neural trajectories of different tasks in the PFC only model and the PFC-MD model.

To empirically demonstrate the challenge of context inference in this regime, we trained a recurrent neural network to continually learn selected pair of tasks from 15 cognitive tasks that test various cognitive functions, including working memory, decision making, categorization, and inhibitory control (Supplementary Fig. 3). Similar to the attention guided task, we trained the neural network to learn two tasks sequentially in two consecutive blocks and switched back to learning the first task in the third block.

To deal with the new challenge, we proposed another form of thalamocortical interaction by separating task learning and context inference into two pathways (task learning and context inference) through the addition of a new PFC-context (PFC-ctx) module (Fig. 5B). The design of the new PFC-ctx module was associated with the experimental observations⁴. Across the PFC-MD network, the MD and the PFC fast spiking neurons were the most informative of the cueing context, whereas the PFC transient neurons were the most informative of the rule (Fig. 5C). We modeled these two types of PFC neurons (transient neurons and fast spiking neurons) as the PFC module and the PFC-ctx module, respectively, in the new framework. In the task learning pathway, supervised learning is used to optimize performance, while the context inference pathway serves to gate the PFC neurons. A critical assumption in this approach is that the connections from input to PFC-ctx are task-disjoint, meaning that during each task, the inputs would target a different group of PFC-ctx neurons. Inputs from different tasks activate different PFC-ctx neurons. Furthermore, we will demonstrate that the PFC-ctx and the MD neurons have different roles in context inference. The learned synaptic weights between different modules of the proposed model are shown in Supplementary Fig. 4. It is worth noting that the PFC-ctx module cannot simply replace the MD module, as demonstrated by our experiments in which we knocked out each module of the model. For example, when we knocked out the MD module but kept the PFC-ctx module, the unstable context encoding in the PFC-ctx module significantly impeded task learning (Supplementary Fig. 5).

To further understand the context encoding abilities of the PFC-ctx and the MD modules, we conducted a study exploring their performance with respect to noise in the PFC-ctx and stability of synaptic connections between the inputs and the PFC-ctx. We parametrically controlled different levels of noise and synaptic stability, where synaptic transmission from the inputs to the PFC-ctx could fail randomly at each time step. We recorded the neural activities of the PFC, the PFC-ctx, and the MD and trained linear classifiers to predict temporal contexts (Fig. 5D, E). Results showed that the MD outperformed both the PFC and PFC-ctx in context encoding. By integrating the neural activities of the PFC-ctx across trials, the MD was able to selectively encode temporal contexts, as shown by a significant performance gap between the PFC-ctx and the MD in terms of context encoding (Fig. 5D), which was consistent with the performance gap between the PFC fast spiking neurons and the MD neurons in the mice experiment data (Fig. 5C). Notably, the MD encodes temporal contexts robustly even in high noise levels and low synaptic stability conditions. This highlights the MD’s ability to encode context information in a low-dimensional space and regulate high-dimensional PFC dynamics in complex cognitive tasks in our newly designed network architecture.

To better illustrate the effect of MD regulation on task representations, we plotted the neural trajectories of different tasks in both the PFC only model and the full model, as shown in Fig. 5F. Our results demonstrate that the inclusion of MD regulation promotes more disjoint and modular task representations in the PFC compared to the PFC only model. Specifically, in the PFC-MD model, the neural trajectories of different tasks do not overlap, further highlighting the effectiveness of MD regulation in promoting task-specific information segregation in the PFC.

Model MD supports continual learning in the PFC

We have demonstrated that the MD component is capable of robustly inferring temporal contexts in various conditions. In this section, we will further show that the MD-to-PFC connections can enable the PFC to perform continual learning of many cognitive tasks, as a consequence of the MD’s context inference.

The role of the MD component is to enable fast, few-trial online context inference and stable context encoding, which can then be used to improve continual learning in complex cognitive tasks. Besides inferring temporal contexts, the MD has two different effects on the PFC: the multiplicative and additive effects, which are context-specific enhancement of neuronal connectivity and suppression of neuronal activities, respectively (Fig. 6A, only the feedback projections from the MD to the PFC in the PFC-MD model are shown.). The multiplicative term models the multiplicative effect of the MD on the total recurrent inputs to individual PFC neurons. It effectively enhances the recurrent inputs for context-relevant neurons. Meanwhile, the additive term suppresses neuronal activities of context-irrelevant PFC neurons. These two terms are inspired by the previous experimental data, which has shown that the MD thalamus has two distinct effects on the PFC neural activity: amplification of local functional connectivity and suppression of neural activity^13,22, corresponding to the multiplicative and additive effects modeled in the neural network, respectively. Additionally, two genetic MD cell types have been identified that have different projections to the PFC, enabling decision making in uncertainty⁴². By incorporating the MD component, the neural representations between distinct temporal contexts become disjoint, facilitating effective population coding within the PFC. The neuronal activities of the PFC with and without the MD are shown in Supplementary Fig. 6.

Fig. 6: The model MD supports continual learning in the PFC.

A The MD effects on the PFC neurons, enhancing current-context PFC activities and inhibiting other-context PFC activities. B The model performance (mean square error, MSE) of the PFC-MD model and the PFC only model during training in the attention-guided behavioral task. C The model performance of the third block when the learned context was switched back. In comparison with the PFC only model, the PFC-MD model had low prediction errors after context switch, alleviating catastrophic forgetting. D The experimental data were collected when mice performed similar three-block switching tasks. The left and middle boxplots show the effect of bilateral MD suppression on behavioral performance. The right boxplot shows the comparison of performance on the consecutive sessions. ***P < 0.001, Bonferroni-corrected rank-sum test. Figure 6D adapted from Fig. 5F of Rikhye, R.V., Gilra, A. & Halassa, M.M. Thalamic regulation of switching between cortical representations enables cognitive flexibility (https://doi.org/10.1038/s41593-018-0269-z). E The model performance of the PFC-MD model and the PFC model. MD suppression significantly degraded the performance when the model switched back to the previous context. ***P < 0.001, Bonferroni-corrected rank-sum test. F The boxplots of the changes in connection weights from the current-context and the other-context PFC neurons to the output neurons during Context 1 and Context 2 presentations. **P < 0.005, ***P < 0.001; statistical test with analysis of variance (ANOVA). Adding an MD component protected synaptic weights in neurons that were not currently context-relevant, which reduces interference in model parameters across different temporal contexts. G The mean performance of the PFC-MD model learning two cognitive tasks in Neurogym sequentially. Orange and green colors represent Task 1 and Task 2, respectively. Shaded areas denote the standard deviations. H We compared the PFC-MD model with two other continual learning methods: EWC and SI, and the PFC only model (left: task 1 performance, right: task 2 performance). The PFC-MD model obtained the best model performance among these methods. I The mean model performance of the PFC-MD model with more cognitive task learned sequentially. The PFC-MD model could flexibly switch between different tasks without forgetting.

We compared the performance of the PFC-MD model with those of the PFC only model in terms of continual learning. The network was trained to perform a three-block switching task, which was similar to the attention-guided behavioral task that mice were trained to do⁴. Notably, the PFC-MD model demonstrated substantially lower output errors when it switches back to a previously experienced context, as shown in Fig. 6B–C. We compared the model performance to the mice experimental data. Mice performed the task well without significant difference in performance across blocks. In contrast, bilateral MD suppression after the second block significantly impaired the performance in the third block (Fig. 6D, left and middle). And this manipulation did not have long-lasting effects (Fig. 6D, right). The performance returned to normal without the MD suppression in the next session. The model performance of the PFC-MD model and the PFC-only model were consistent with the mice experiment data under the manipulation in the three-block framework (Fig. 6E). MD suppression significantly degraded the task performance when the model switched back to the previous context.

The continual learning performance benefited from the MD-mediated inhibition. The PFC-MD model had a weight protection mechanism on the learned contexts, as shown in Fig. 6F. The weight changes of the other-context connections with the MD were significantly smaller than those without the MD in the same contexts. In other words, the PFC-MD model protected the synaptic weights in neurons that were not currently context-relevant. By inferring temporal contexts and targeting context-relevant neurons in the PFC, the MD component allowed the PFC to restrict learning to the task-relevant population. Consequently, adding an MD component protected synaptic weights in neurons that were not currently task-relevant. More specifically, by providing an inhibitory control signal to task-irrelevant prefrontal networks, the MD thalamus prevents them from becoming engaged and thereby preserves their synaptic weights from being adjusted through activity-dependent synaptic plasticity between the PFC and the MD. The weight protection mechanism was validated by the mice experiment data as well in the previous study⁴. The experiment data suggested that context-relevant functional connections rapidly stabilized, protecting recently engaged but currently irrelevant connectivity patterns, which were consistent with the weight protection in the PFC-MD model. More details about the mice data were shown in the previous study⁴.

We further evaluated continual learning performance on more general cognitive tasks in Neurogym⁴³ shown in Fig. 6G. With the effect of MD regulation on the PFC, the MD allows non-overlapping groups of the PFC neurons to be activated in each context. Specifically, The MD neurons maintain the activities of current context-relevant and inhibit the activities of current context-irrelevant PFC neurons. The synaptic weights between the MD and the PFC were randomly generated and fixed during learning. Consequently, there was no catastrophic interference between tasks, and the PFC-MD model preserved perfect performance when switching from task 1 to task 2 (Fig. 6G).

Recently, various continual learning approaches have been proposed using different strategies in different scenarios. Among them, two widely used plasticity-based methods are elastic weight consolidation (EWC)³⁴ and synaptic intelligence (SI)³³. Both algorithms evaluate the importance of synaptic connections for each task at the end of each training block. They selectively slow down learning on the important weights for past tasks and use the unimportant weights of past tasks for learning in future tasks to reduce catastrophic forgetting. However, the estimation of weight importance and the control of learning might not be accurate across tasks in practice. We compared the model performance of the PFC-MD model with those of the EWC and SI models in Fig. 6H. The PFC-MD model outperformed the other continual learning models. The weight protection of our model against catastrophic forgetting is stronger than that of the regularization-based methods, such as EWC and SI. Regularization-based methods offer a ‘soft’ protection of synapses deemed important for previously learned tasks by penalizing changes to these synapses. In contrast, the PFC-MD model utilizes modular structures for learned tasks through the MD gating, allowing for stronger weight protection. To test whether the initialization in the PFC recurrent weights influences the performance, we performed the experiments with different initialization in the PFC recurrent weights: the scaled identity matrix and random orthogonal initialization⁴⁴. Both initializations are orthogonal, making gradient backpropagation more efficient⁴⁵. The results of the scaled identity matrix were shown above while similar performance was obtained with random orthogonal initialization (Supplementary Fig. 7).

We evaluated the continual learning performance with more cognitive tasks involved, e.g., three tasks were learned sequentially (Fig. 6I). However, scaling up the number of cognitive tasks to learn is not straightforward. Learning three tasks could be more challenging than learning two tasks in terms of more computational interference across tasks during learning. Synaptic plasticity must balance learning and forgetting of synaptic weights associated with learned and future tasks in order to alleviate catastrophic forgetting. From the results (Fig. 6I), we can see that the PFC-MD model can perform continual learning without forgetting and flexibly switch between multiple cognitive tasks. In comparisons with other baseline methods, e.g., EWC and SI, the PFC-MD model achieved the best continual learning performance in multiple-task learning (Supplementary Fig. 8A). Results involving more tasks were obtained because of the adaptive thresholding, one of the key principles in the PFC-MD synaptic plasticity. The principle allowed for faster context learning than context forgetting (Supplementary Fig. 8B). Therefore, the PFC-MD model is able to encode multiple temporal contexts and learn different cognitive tasks sequentially without forgetting. It should be noted that although context inference is rapid, previously learned contexts should not be forgotten because task re-learning in contexts requires more resources from scratch.

Forward transfer of the PFC-MD model with task similarity measurement

So far, we have demonstrated that introducing an MD model can alleviate catastrophic forgetting and facilitate continual learning in the PFC. However, beyond merely avoiding forgetting, human and animal brains exhibit a high degree of flexibility in transferring knowledge from previously learned tasks, a phenomenon known as forward transfer. Specifically, forward transfer refers to the ability that previously learned tasks improve both the performance and learning efficiency on related future tasks³⁰. Unfortunately, the MD effects we imposed on the PFC-MD model prohibit forward transfer, as the disjoint subsets of PFC neurons dedicated to specific tasks do not overlap, meaning that there are no shared neurons involved in common computations across similar tasks. The disjoint PFC-MD model effectively learns each task in a separate network. Our experimental results thus far demonstrate that the clustered PFC neurons resulting from the disjoint MD effects enable continual learning, but not forward transfer. In this section, we will explore the effect of relaxing the disjoint input assumptions.

In contrast to the MD effects that operate on distinct PFC neuron subsets discussed in previous sections, a fraction of PFC neurons is selected to not receive inhibition from all context-selective MD neurons. In addition to inhibiting task-irrelevant PFC neurons, context-selective MD neurons maintain the activities of some common PFC neurons across tasks, as shown in Fig. 7A. The MD-to-PFC projections can be manipulated based on task similarity (see “Methods” section). Therefore, task representations in the PFC can be either totally or partly modular, corresponding to the disjoint or overlapping MD-to-PFC effects (Fig. 7A).

Fig. 7: Forward transfer of the PFC-MD model with the task similarity measurement.

A To enable the PFC-MD model with the ability of forward transfer, the MD gating of different tasks is overlapped on some PFC neurons so that cognitive tasks share a subset of PFC neurons. B The task similarity is measured by the inner product of task variance, which is obtained from one recurrent neural network with interleaved training. C The mean performance of the PFC-MD model with different MD-to-PFC effects, and similar and non-similar task pairs to learn. The disjoint PFC-MD model didn’t have forgetting for learned tasks regardless of task similarity but had no forward transfer, while the overlapping PFC-MD model obtained performance improvement in terms of forward transfer. D The mean continual learning (CL) and forward transfer (FT) performance with varying task similarity in the disjoint and overlapping MD-to-PFC projections. The error bars denote the standard deviations.

To determine the task transferability and the corresponding MD-to-PFC effects, we need to quantify the task similarity across different cognitive tasks. Here, we quantified the task similarity according to the task representations in a recurrent neural network²⁷ (Fig. 7B). Basically, a single-hidden layer recurrent neural network learns multiple cognitive tasks simultaneously with interleaved training. With task variance analysis²⁷, we computed the task variance value of each hidden unit for the tasks. Task variance vectors are more similar across similar cognitive tasks (Supplementary Fig. 9). Task similarity is then quantified by the inner product of task variance vectors between two tasks (Fig. 7B).

We showed the mean performance of the PFC-MD model with disjoint or overlapping MD-to-PFC effects, and similar and non-similar task pairs in Fig. 7C. The disjoint PFC-MD model exhibited no forgetting of learned tasks regardless of task similarity, as shown in Fig. 6E. However, this model was unable to transfer knowledge from previously learned tasks to future tasks, i.e., it lacked forward transfer. In comparison, the overlapping PFC-MD model exhibited more forgetting but also demonstrated more forward transfer, especially for similar task pairs.

We analyzed how the model performance changed with varying task similarity in the disjoint and overlapping MD-to-PFC projections, respectively (Fig. 7D). The continual learning (CL) and forward transfer (FT) performance were defined as task 1 performance at the end of block 2 and task 2 performance at the end of block 1, respectively. The disjoint PFC-MD model achieved perfect continual learning but no forward transfer across all levels of task similarity. In contrast, the overlapping PFC-MD model experienced a drop in performance in terms of continual learning but obtained a performance improvement in forward transfer, indicating a trade-off between preventing forgetting and facilitating forward transfer. From the results, we found the performance of forward transfer were highly dependent on the level of task similarity. Specifically, when the tasks to be learned were more similar, the overlapping PFC-MD model achieved higher performance in forward transfer.

We compared the forward transfer performance with those of the baseline models, namely EWC, SI, and the PFC only models, and found similar relationships between forward transfer and task similarity (Supplementary Fig. 10A–B). All models exhibited positive correlations between forward transfer performance and task similarity. Although the baseline methods could achieve forward transfer due to their weight penalty mechanisms across tasks, their continual learning performance decreased as the learned cognitive tasks became more similar (as evidenced by negative correlations in continual learning vs. task similarity). In contrast, the PFC-MD model with the overlapping effects demonstrated moderate improvements in both continual learning and forward transfer with more similar tasks. Further details regarding the performance of continual learning and forward transfer as a function of task similarity are shown in Supplementary Fig. 10C.

Discussion

Associative cortical areas, particularly the prefrontal areas, are heavily involved in numerous cognitive processes. Recent studies have suggested that the mediodorsal thalamus encodes the temporal context and regulates PFC dynamics accordingly. In this study, we developed a PFC-MD model with a recurrent neural network and synaptic plasticity for learning multiple cognitive tasks sequentially. Our proposed Hebbian learning-based synaptic plasticity between the PFC and the MD allows the MD to robustly infer temporal contexts. The MD enhances the context-relevant recurrent inputs and suppresses the context-irrelevant neuronal activities in the PFC neurons, making the PFC modular for different temporal contexts. The model results validated the experimental findings in the attention-guided behavior task in mice⁴. Furthermore, we scaled up the PFC-MD model to learn multiple complex and general cognitive tasks. We found that the MD could robustly infer the temporal contexts and the PFC-MD model learned multiple cognitive tasks without forgetting. The PFC-MD model outperformed other methods in terms of continual learning performance. Finally, we enabled the PFC-MD model with the ability of forward transfer with the overlapping MD effects on the PFC. The proposed model had the feasibility of continual learning and transfer learning with the disjoint and overlapping MD-to-PFC projections.

The biological implementation of the computations needs further investigation. We highly considered the biological plausibility when we designed the PFC-MD synaptic plasticity: (1) the MD was model as a feed-forward neural network given no recurrence found in the MD neurons^19,46; (2) the PFC-MD synaptic plasticity was based on the Hebbian learning rule, which is a widely used learning rule in brain-like computing⁴⁷; (3) the three key components: pre-synaptic and post-synaptic traces, winner-take-all, and adaptive thresholding could be possibly implemented in the brains, which were widely used in previous work as well; (4) the assumption that different subsets of PFC neurons are more active than others in each context and the MD encodes temporal contexts was inspired by the experiment data in Rikhye et al.⁴. We have shown some comparisons between the model outputs and the experiment data. However, more experiment evidence should be explored for implementing these computations.

We experience our daily activities continuously, yet these experiences are segmented into distinct events in perception and memory by contextual changes known as event boundaries^48,49,50. Previous cognitive studies have showed that event boundaries are determined by the changes of external stimulation and internal goals. However, computational models that can infer temporal contexts from continuous activities are not well-understood. In this paper, we develop an MD component with synaptic plasticity that interacts with the PFC to enable the rapid and online inference of temporal contexts. The inference of temporal contexts is performed continuously and quickly adapts to new contexts while the main PFC neural network is learning various cognitive tasks. However, it should be noted that the term context might have different meanings in different domains. In our study, the context is about the combinations of sensory cues or task identification. The potential use of our PFC-MD model in other contexts (e.g., the probability of receiving a reward for a given choice) needs further investigations. Another limitation of our PFC-MD synaptic plasticity is that the MD representation of temporal context is a discretized representation of the first principal component of the time-averaged PFC activities. But temporal context may not necessarily be encoded as the first principal component of neural activities in all situations.

Unlike other continual learning approaches such as EWC and SI that constrain key model parameters at the end of each context, our proposed framework infers temporal contexts online while learning complex cognitive tasks at the same time. Some continual learning approaches provide explicit task identifications directly to the models during training, e.g., an one-hot encoding vector of task identification was given to recurrent neural networks as well as the inputs³. A recent neural network model of human continual learning was proposed by augmenting standard supervised training with Hebbian learning, where a “sluggish” task signal was directly introduced without automatic inference to compare model performance of blocked and interleaved training⁵¹. Rapid and online inference of temporal contexts with biological plausibility is the fundamental difference from existing continual learning. In our experimental setups, the PFC-MD model was trained in a blocked manner. Blocked training strengthens the ability to link the context-specific neurons to the corresponding MD neurons, allowing the MD model to infer temporal contexts. However, we should acknowledge the limitation of our study that the context here represents pairs of stimuli that appear in blocks or task identification. Distinct populations are activated in the PFC in different contexts. In the real world, we process a continuous stream of sensorimotor experience and our brain infers context based on experiences with tasks. Meanwhile, under naturalistic conditions, context is typically uncertain. Our study demonstrates a thalamocortical framework for context inference but more investigations on the computational and neural bases of context-dependent learning are needed⁵².

Learning in artificial and biological neural systems requires both plasticity and stability to integrate new knowledge and to prevent forgetting of previous knowledge, respectively, known as the stability-plasticity dilemma. Previous studies have examined how different task variables contribute to addressing this dilemma. Some evidence suggests that the brain may use orthogonal representations to minimize interference between tasks^53,54. In contrast, disentangling the neural representations of different contexts or tasks into totally separate activated modules is an ideal solution but might not be practical due to inefficient representations of different contexts or tasks. Especially, these kinds of methods lack the capability of knowledge transfer between contexts or tasks. A recent human study has showed that neurons in the medial frontal cortex encoding various task variables were intermixed, forming a representational geometry that simultaneously allowed task specialization and generalization⁵⁵. Computationally, task-general neurons learn common knowledge across tasks, while task-specific neurons learn private knowledge of individual tasks, which allows knowledge transfer between tasks and maintain good performance in each task as well. However, it remains unclear how distinct groups of neurons with different functionalities collaborate to facilitate multiple-task learning.

There are two distinct perspectives about where neural computation is performed in the brain. One perspective suggests that each individual neuron has a specific computational function with distinct response profiles. For instance, distinct groups of neurons in the orbitofrontal cortex have been identified, each with a particular response profile in task-variable space⁵⁶. The other perspective suggests that neural computation is performed at the level of an entire population, with neural dynamics in a low-dimensional manifold.⁵⁷ Task variables are distributed randomly across neurons.⁵⁸ However, our current understanding of how to align both individual response profiles at a neuron level and neural dynamics at a network level remains limited. A recent study has showed that the dimensionality of the dynamics and subpopulation structure play complementary roles.^59,60 Various tasks can be implemented with different sizes of neural networks with fully random populations. However, complex and flexible tasks require multiple subpopulations. Distinct groupings with different functionality allows for more flexible input-output mappings and are modulated differently as a gain control mechanism, specifically for context-dependent tasks. In the study, we have explored both computation mechanisms, i.e., individual response profiles on the attention-guided behavioral task and neural dynamics with subpopulation structures on the NeuroGym cognitive tasks. But how to flexibly target a sparse random subset of PFC neurons for activation for individual contexts and organize distinct groupings with different functionality remains an unsolved question.

We leverage both task general (overlapping MD-to-PFC effects) and task specific (disjoint MD-to-PFC effects) representations to enable the balance between forward transfer and continual learning in our PFC-MD model. However, a limitation of our study is that we did not measure task similarity over time for the forward transfer experiments, and further investigation is needed to determine how to compute the similarity among multiple tasks. To address this issue, an additional module could be added to analyze and compare current tasks with previously learned tasks to provide an online measurement of task similarity.⁶¹ A potential promising approach to solve this question in continual learning is to incorporate a memory module that can replay previous tasks^37,62,63. Notably, studies have shown that the relationship between task similarity and forgetting is non-monotonic, and intermediate task similarity is usually most damaging^64,65. Thus, further investigations are necessary to determine how the memory replay affects the relationship between task similarity and forgetting.

Another critical component of the model is the gating in the prefrontal cortex. The gating is utilized in the prefrontal cortex to minimize interference between different tasks¹. It is used to not only control switching between already learned tasks, but also to learn novel tasks without forgetting. In our model, the gating is implemented with the MD effects based on the findings of the PFC-MD interactions in cognitive flexibility. It has also been suggested that basal ganglia could regulate the gating of PFC representations⁶⁶. However, gating is typically hand-crafted^67,68,69. We demonstrate how Hebbian learning between the PFC and the MD can facilitate gating learning. Similarly, a Hebbian training step was shown to learn the gating scheme from scratch⁵¹. However, there is a need for further research into more learnable and flexible gating schemes that consider multiple tasks simultaneously, especially when the similarity among them varies.

The MD thalamus has dense projections to the prefrontal cortex, a brain region heavily involved in cognition¹¹. Individual MD neurons can target multiple prefrontal regions. In our PFC-MD model, the MD neurons maintain the context-relevant neural activities and suppress the context-irrelevant neural activities in the PFC. Various computational models have been proposed to model the role of thalamus in cognition. Our model is highly related to the recent work by Hummos et al.^70,71, which proposed thalamocortical neural models in cognitive flexibility. Their PFC-MD frameworks were similar with the MD mediation on the PFC. However, their models had limited MD neurons (e.g., 2 neurons) and reservoir neural networks in the PFC⁷⁰. The block change points were estimated by another module, rather than the MD in the unified framework as our work. In the Thalamus model⁷¹, there were feedback projections from the PFC population outputs instead of the individual PFC neurons.

Experiments showed that damage to the MD can cause diminished behavioral flexibility and working memory impairment^72,73. In particular, patients with the MD damage have difficulty with tasks that require rapid cognitive switching⁷³. These findings demonstrate the critical role of the MD in cognitive flexibility⁷⁴. The thalamus has undergone substantial expansion and variation throughout evolution^75,76. The thalamus, even the MD, is believed to perform a broad range of computations and inform the cortex about expected outcomes or changes in key task-relevant variables⁷⁶. The thalamus receives rich stimulus-related information from sensory cortices and performs computational effects on the prefrontal areas. The evolutionary and developmental trajectory of the thalamus highlights its unique role in flexible behaviors. These potential task indicators would be beneficial to train task learning neural networks with task identification. A component consisting of task context/rule activations and sensory cortices integrate in association cortex to produce conjunctive activations for cognitive flexibility in the Guided Activation Theory^1,77. Therefore, the MD thalamus component has the potential to facilitate continual learning.

To conclude, we propose a PFC-MD neural network model that allows rapid, online context inference using a Hebbian plasticity rule. Specifically, an MD thalamus-like component is incorporated to infer temporal contexts and gate context-irrelevant neurons in the recurrent neural network of the PFC. The MD can effectively infer temporal contexts online in a few trials and adapt to different contexts. There are three primary properties in the PFC-MD model: the PFC-to-MD synaptic plasticity with pre-synaptic traces and adaptive thresholding, and winner-take-all normalization in the MD. These properties enable the recurrent neural network to learn different cognitive tasks sequentially. The proposed model offers significant computational advantages in terms of continual learning and knowledge transfer.

Methods

Network structure

We use a recurrent neural network to model the PFC. The rate of each neuron is defined as ${r}_{i}^{PFC}=tanh({I}_{i})$ if I_i > 0 and 0 otherwise, where I_i is the input of neuron i. The input consists of cue input, recurrent input, and MD gating. The neural dynamic of the reservoir neurons is defined with a exponential decay as follows

$${\tau }_{PFC}\frac{d{I}_{i}(t)}{dt}= -{I}_{i}+{\sum}_{k}{w}_{ik}^{in}cu{e}_{k}(t)+{\sum}_{j}(1+{\mu }_{i}(t)){w}_{ij}{r}_{j}^{PFC}(t) \\ +\frac{2}{L}{\sum}_{l}{w}_{il}^{MD+}{r}_{l}^{MD}(t),$$

(2)

where τ_PFC = 20 ms is the time constant of the PFC, L is the number of the MD neurons, cue_k is a one-hot vector, where each element corresponds the presentation of a specific cue. The entry is 1 if the corresponding cue is on and 0 for those off. The input weights ${w}_{ik}^{in}$ are set such that each cue k stimulates a set of 200 neurons, disjoint with the sets for other cues, with each weight chosen uniformly between 0.75 and 1.5. w_ij is initialized with a Gaussian distribution with mean=0 and standard deviation=$0.75/\sqrt{400}$ and the mean is subtracted across each row of the matrix. ${r}_{l}^{MD}$ is a vector representing the MD neuron activity. ${w}_{il}^{MD+}$ is set with a Gaussian distribution with mean=0 and s.d.=1. μ_i mediates the multiplicative effect of the MD on the total recurrent input to neuron i and is given by

$${\mu }_{i}=\frac{2}{L}{\sum}_{l}{w}_{il}^{MD\times }{r}_{l}^{MD},$$

(3)

where ${w}_{il}^{MD\times }$ is set with a Gaussian distribution with mean=0 and s.d.=1.

The neural dynamic of the MD neuron l is modeled as follows

$${\tau }_{MD}\frac{d{V}_{l}(t)}{dt}=-{V}_{l}+{\sum}_{j}{w}_{lj}^{PFC}{r}_{j}^{PFC}(t),$$

(4)

where V_l is the input of MD neuron l and τ_MD is the MD time constant, which is 4 × τ_PFC. The MD neurons decay more slowly than the PFC neurons in order to integrate the PFC inputs. ${r}_{j}^{PFC}(t)$ is the PFC output. ${w}_{lj}^{PFC}$ is the synaptic weights from the PFC to the MD, which is initialized randomly with a Gaussian distribution with mean=0 and s.d.=1. Here we have L MD neurons, each subset of the MD neurons encodes individual context. We use adaptive multilevel thresholding as normalization to calculate the MD neuron activity ${r}_{l}^{MD}$ given the input V_l. By comparing all inputs $V,{r}_{l}^{MD}$ is set to 1 if the input V_l is within the top K largest and 0 otherwise.

$${r}_{l}^{MD}(t)=\left\{\begin{array}{ll}1&\,{{\mbox{Top}}}\,\,K\,\,{{\mbox{high}}} \, {{\mbox{membrane}}} \, {{\mbox{potential}}}\,\,V\,\,{{\mbox{in}}}\,\,L\,\,{\mbox{MD neurons}}\,\\ 0 & \,{\mbox{Otherwise}}\,,\hfill \end{array}\right.$$

(5)

where K is the number of MD neurons to encode a context.

We use the Hebbian plasticity to learn the synaptic strengths ${w}_{il}^{MD+},{w}_{il}^{MD\times }$ and ${w}_{lj}^{PFC}$ between the PFC and the MD.

$$\Delta w(t)=\eta \left({r}_{post}^{MD}(t)-0.5\right)\otimes \left({r}_{pre}^{MD}(t)-{\theta }_{pre}(t)\right),$$

(6)

$${r}_{pre}^{MD}(t)={r}_{pre}^{MD}(t-1)+\frac{1}{5T}\left(-{r}_{pre}^{MD}(t-1)+{r}^{PFC}(t)\right),$$

(7)

$${\theta }_{pre}(t)=\frac{1}{N}{\sum}_{i}{r}_{i,pre}^{MD}(t),$$

(8)

$${\tilde{r}}_{trace}^{MD}(t)={\tilde{r}}_{trace}^{MD}(t-1)+\frac{1}{5T}\left(-{\tilde{r}}_{trace}^{MD}(t-1)+{r}^{MD}(t)\right),$$

(9)

$${r}_{post,i}^{MD}(t)=\left\{\begin{array}{ll}1&\,{{\mbox{Top}}}\,\,K\,\,{{\mbox{high}}} \, {{\mbox{activities}}} \, {{\mbox{in}}}\,\,{\tilde{r}}_{trace}^{MD}(t)\\ 0&\,{\mbox{Otherwise}}\,,\hfill \end{array}\right.$$

(10)

where r^MD is the MD output vector, r^PFC is the PFC output vector, η is the Hebbian learning rate, ${r}_{pre}^{MD}$ is the MD pre-synaptic traces (the PFC outputs) filtered over 5 trials, and ${r}_{post,i}^{MD}$ is the ith MD post-synaptic trace after normalization forming the vector of the MD post-synaptic traces ${r}_{post}^{MD}$. T is the total time steps in a trial. The synaptic weights between PFC and MD can be updated with Δw. The update for PFC → MD and MD → PFC is as follows,

$${w}^{PFC}(t)={w}^{PFC}(t-1)+\Delta w(t),$$

(11)

$${w}^{MD+}(t)={w}^{MD+}(t-1)+0.1 * \Delta {w}^{T}(t),$$

(12)

$${w}^{MD\times }(t)={w}^{MD\times }(t-1)+0.1 * \Delta {w}^{T}(t).$$

(13)

The synaptic weights are clipped if the values are larger or smaller than some thresholds. The value intervals of w^PFC, w^MD+, and w^MD× are [0, 1], [-10, 0], [0, 7] or [0, 0.75], respectively. In the PFC-MD model, the additive weights w^MD+ are always negative, which represent the MD suppression on the other-context PFC neurons. The multiplicative weights w^MD× are always positive, which represent the MD enhancement on the current-context PFC neurons.

For the attention-guided behavioral task, the model has two output neurons corresponding to two rules: attend to vision and attend to audition. The neural dynamic of the readout units is modeled as

$$\tau \frac{d{I}_{n}^{out}}{dt}=-{I}_{n}^{out}+{\sum }{{w}_{ni}^{out}} \, {r}_{i}.$$

(14)

The output is ${r}_{n}^{out}=tanh({I}_{n}^{out})$ if ${I}_{n}^{out} \, > \, 0$, and 0 otherwise. ${w}_{ni}^{out}$ is initialized to zero and updated in an error-driven way as follows,

$$\Delta {w}_{ni}^{out}=-{\eta }^{out}{r}_{i}\left({r}_{n}^{out}-{r}_{n}^{target}\right),$$

(15)

where η^out is the learning rate, ${r}_{n}^{out}$ is the model output, and ${r}_{n}^{target}$ is the target output of the readout neuron n.

Modified network architecture with separate task learning and context inference pathways

To deal with more general cognitive tasks, we propose another form of thalamocortical interaction: separating task learning and context inference into two pathways by adding a new PFC-context (PFC-ctx) module. Besides the sensory input and readout layers, the network consists of three functional area: PFC, PFC-context (PFC-ctx), and MD.

PFC layer

We use a continuous-time recurrent neural network to model PFC, which receives inputs from the input layer, other PFC neurons and the MD neurons.

$${\tau }_{PFC}\frac{d{I}_{i}^{PFC}\left(t\right)}{dt}= -{I}_{i}^{PFC}\left(t\right)+{\sum}_{k}{w}_{ik}^{in\to PFC}{s}_{k}\left(t\right) \quad\quad\quad\quad (\,{{\mbox{External}}})\\ +{\sum}_{j}{w}_{ij}^{rec}{r}_{j}^{PFC}\left(t\right) \quad\quad\quad\qquad\qquad\qquad (\,{{\mbox{Recurrent}}})\\ +\frac{2}{L}\left({\sum}_{l}{w}_{il}^{MD\to PFC}{\tilde{r}}_{l}^{MD}\left(t\right)-b\right) \quad\quad (\,{{\mbox{MD}}}),$$

(16)

$${{r}_{i}^{PFC}}\left(t\right)=ReLU\left({{I}_{i}^{PFC}}\left(t\right)\right),$$

(17)

where L denotes the number of MD neurons and the default value for the inhibition b is 5.

We use uniform noise to initialize input to PFC weight ${W}^{in \to PFC}=\left({w}_{ik}^{in \to PFC}\right)$. The values are initialized from $U\left(-\sqrt{\frac{1}{{N}_{input}}}, \sqrt{\frac{1}{{N}_{input}}}\right)$, where N_input means the size of input layer. We use the scaled identity matrix 0.5 ∗ I to initialize PFC recurrent weight ${W}^{rec}=\big({w}_{ij}^{rec}\big)$. We also reproduce results with random orthogonal initialization⁴⁴ (see Supplementary Fig. 7). Both initializations are orthogonal, making gradient backpropagation more efficient⁴⁵. The MD neurons maintain current-relevant and inhibit current-irrelevant PFC neurons. This effect is implemented as disinhibition in the model. PFC neurons are inhibited when MD is silent. b is the inhibition level. Each activated MD neuron disinhibits a part of PFC population and cancel the base-level inhibition. The disinhibition is realized through MD to PFC weight ${W}^{MD\to PFC}=\left({w}_{il}^{MD\to PFC}\right)$. W^MD→PFC is randomly generated and fixed under the assumption that each PFC neuron is connected to only one randomly chosen MD neuron. The weight value matches the inhibition level b.

In the attention-guided behavioral task, the inputs are static, and the recurrent network requires no learning; hence, the MD has two gating effects on the PFC: multiplicative gating on the recurrent inputs from other PFC neurons and additive gating on the PFC activities. However, in complex cognitive tasks, recurrence learning is performed by error back-propagation from the output neurons within trials. In contrast, multiplicative gating of the MD on the recurrence is tuned based on the recently activated task-relevant neurons. Due to the variability in PFC activities that arises from within-trial dynamics, across-trial differences, and learning, recurrence learning from the task optimization via back-propagation and multiplicative gating from the local PFC-MD synaptic plasticity might not be performed synchronously (Fig. 5A). Multiplicative gating of the MD on the recurrence is not appropriate for complex cognitive tasks with recurrence dynamics. Therefore, for complex cognitive tasks, we simplified the projections from the MD to the PFC: instead of containing both multiplicative and additive terms, the MD here gates PFC activities in a context-dependent way.

PFC-context (PFC-ctx) layer

PFC-ctx is a feedforward layer receiving external inputs and projecting to MD.

$${r}_{m}^{PFCctx}\left(t\right)=ReLU\left({g}_{m}\cdot {\sum}_{k}{w}_{mk}^{in\to PFCctx}{s}_{k}\left(t\right)+\epsilon \right),$$

(18)

where g_m and ϵ are activation probability and Gaussian noise, respectively. The synaptic transmission between input and PFC-ctx layer is probabilistic. Although for each task, the input layer is connected to disjoint neurons in the PFC-ctx layer, whether these neurons of the PFC-context layer can receive sensory inputs is determined by a random variable ${g}_{m} \sim B\left(1,\, p\right)$, which is called activation probability. Meanwhile, we apply Gaussian noise to the PFC-context layer $\epsilon \sim N\left(0,\, {\sigma }^{2}\right)$. In the experiments, we set p = 0.40 and σ = 0.01.

We use positive uniform noise to initialize input to PFC-ctx weight ${W}^{in\to PFCctx}=\left({w}_{mk}^{in\to PFCctx}\right)$. The values are initialized from $U\left(0,\sqrt{\frac{1}{{N}_{PFC}}}\right)$. We further assume disjoint projection from input layer to PFC-ctx layer. The input layer would only be connected to a subset of PFC-context neurons for each task. And when task switching occurs, the input layer would send inputs to a different subset of PFC-context neurons. Nonetheless, this assumption is not equivalent to explicitly giving task identity (see Fig. 5 D and Supplementary Fig. 5).

MD layer

The MD is a feedforward layer with Hebbian-like synaptic plasticity.

$${\tau }_{MD}\frac{d{r}_{l}^{MD}\left(t\right)}{dt}=-{r}_{l}^{MD}\left(t\right)+{\sum}_{m}{w}_{lm}^{PFCctx\to MD}{r}_{m}^{PFCctx}\left(t\right).$$

(19)

We use Gaussian noise to initialize the PFC-ctx to MD weight ${W}^{PFCctx\to MD}=\left({w}_{lm}^{PFCctx\to MD}\right)$. The values are initialized from $N\left(\mu=0,\, \sigma=\sqrt{\frac{1}{{N}_{MD}*{N}_{PFCctx}}}\right)$, where N_MD and N_PFCctx are the sizes of the MD and the PFC-ctx layers, respectively. The noise is used to activate the MD neurons in the beginning of training. We apply winner-take-all as normalization to the MD membrane potential ${{{{\boldsymbol{r}}}}}^{MD}\left(t\right)$. And the temporal context is represented in low dimensional all-or-none MD activities.

$${\tilde{ r}}_{l}^{MD}\left(t\right)=\left\{\begin{array}{ll}1,\quad &\,{{\mbox{Top}}} \, {{\mbox{K}}} \, {{\mbox{high}}} \, {{\mbox{membrane}}} \, {{\mbox{potential}}} \, {{\mbox{in}}}\,\,{{{{\boldsymbol{r}}}}}_{l}^{MD}\left(t\right)\\ 0,\quad &\,{\mbox{Otherwise}}\,,\hfill\end{array}\right.$$

(20)

where K is the number of MD neurons activated in one temporal context.

Output layer

The output layer receives inputs from the PFC layer and makes a action.

$${r}_{n}^{out}\left(t\right)={\sum}_{i}{w}_{ni}^{out}{r}_{i}^{PFC}\left(t\right).$$

(21)

We use uniform noise to initialize PFC to output weight ${W}^{out}=\left({w}_{ni}^{out}\right)$. The values are initialized from $U\left(-\sqrt{\frac{1}{{N}_{PFC}}},\sqrt{\frac{1}{{N}_{PFC}}}\right)$, where N_PFC means the size of PFC layer.

Update of synaptic weights

In the network, W ^in→PFC, W ^rec and W ^out are optimized with supervised learning. We use Adam optimizer to minimize the mean square error (MSE) between the network output and the target output⁷⁸. We update the weights at every timestep and the learning rate in the ADAM optimizer is 1e − 4. The mini-batch size is set to 1. The PFC-ctx to MD weight W^PFCctx→MD is optimized with the modified Hebbian learning,

$$\Delta {w}_{lm}\left(t\right)=\eta \cdot \left({\tilde{r} }_{post,l}\left(t\right)-0.5\right)\cdot \left({\tilde{r} }_{pre,m}\left(t\right)-{\tilde{\theta }}_{pre}\left(t\right)\right),$$

(22)

$${w}_{lm}^{PFCctx\to MD}\left(t\right)={w}_{lm}^{PFCctx\to MD}\left(t-dt\right)+\Delta {w}_{lm}\left(t\right),$$

(23)

where η is the Hebbian learning rate. η should be small for the stability of modified Hebbian learning. We set η = 1e − 5. The PFC-ctx to MD weights accumulate over time. We set the upper bound of the weight values to 2.0. The upper bound affects the convergence time of PFC-ctx to MD weight. ${\tilde{r} }_{pre,m}\left(t\right)$ is binarized presynaptic trace of PFC-ctx unit m. ${\tilde{\theta} }_{pre}\left(t\right)$ is the threshold of binarized presynaptic traces. ${\tilde{r} }_{post,l}\left(t\right)$ is postsynaptic trace of MD unit l.

Binarized presynaptic traces

We keep presynaptic traces and compute binarized presynaptic traces at every timestep. We define the presynaptic traces with dynamics as:

$${\tau }_{pre}\frac{{dr}_{pre,m}\left(t\right)}{dt}=-{r}_{pre,m}\left(t\right)+{r}_{m}^{PFCctx}\left(t\right),$$

(24)

where τ_pre is the time constant of presynaptic traces. It controls the time span of PFC-ctx activity information that MD integrates. Thus, it significantly affects the modified Hebbian learning. If the value is too small, the time span of information integration would be too short to capture all context-relevant neurons. If the value is too large, the dynamic is too slow. The model would fail to recognize a context switch rapidly. The presynaptic traces are binarized according to a mean threshold,

$${\tilde{r} }_{pre,m}\left(t\right)=\left\{\begin{array}{ll}1,\quad &{r}_{pre,m}\left(t\right) \, \ge \, {\theta }_{pre}\\ 0,\quad &{r}_{pre,m}\left(t\right) \, < \, {\theta }_{pre},\end{array}\right.$$

(25)

$${\theta }_{pre}=mean\,\left({{{{\boldsymbol{r}}}}}_{pre}\left(t\right)\right).$$

(26)

Threshold of binarized presynaptic traces

We define the threshold of binarized presynaptic traces as:

$${\tilde{\theta} }_{pre}=c \cdot mean\left({\tilde{{{\boldsymbol{{r}}}}} }_{pre}\left(t\right)\right).$$

(27)

Instead of a hard-coded threshold, the threshold of presynaptic traces ${\tilde{{{\rm{\theta}}}}}$_pre is adaptive to varying presynaptic traces. c is a hyperparameter controlling the timescales of learning and forgetting. We set c = 0.6 so that the learning of current context-specific connection is faster than the forgetting of other connections.

Postsynaptic traces

We define the postsynaptic traces as:

$${\tau }_{post}\frac{d{\tilde{r} }_{post,l}\left(t\right)}{dt}=-{\tilde{r} }_{post,l}\left(t\right)+{\tilde{r} }_{l}^{MD}\left(t\right),$$

(28)

where τ_post is the time constant of postsynaptic traces. Similar to τ_pre, τ_post controls the time span of MD activity information that MD integrates. It should be an intermediate value so that context-relevant MD neurons are captured and MD is also sensitive to context switch.

Task structure

We have two kinds of cognitive tasks in our experiments: the attention-guided behavior task and more general tasks in Yang19 collection²⁷. For the first scenario, the neural networks are trained in alternating blocks following the study of Rikhye and colleagues. Cues 1 and 2 are used in context 1, while cues 3 and 4 used in context 2. Block 3 returns to context 1 to evaluate the model performance in continual learning. The cue inputs are implemented with multi-dimensional vectors with each dimension representing one cue in the continuous scale between 0 and 1 (with random noise). The number of time steps per trial is 200.

For the second scenario, we test our model with cognitive tasks that are widely used in neuroscience and psychological studies. These tasks share similar structure and consist of several families, Matching family: DMS, DNMS, DMC, DNMC; Decision-Making family: DM 1, DM 2, Ctx DM 1, Ctx DM 2, MultSen DM; Go family: Go, RT Go, Dly Go; Anti-Go family: Anti, RT Anti, Dly Anti. For training purposes, tasks are organized into trials (~ 20 timesteps), and each trial consists of 4 periods: fixation, stimulus, delay, response. Stimulus period replaces the delay period for tasks without delay. The input dimension of tasks is a concatenation of fixation and a stimulus modality. The binary fixation input is set to 1 when the model should fixate and 0 during response period. The stimulus modality containing sensory information inputs is simulated as two rings, each of which is 16 units representing a circular variable. The preferred direction of units in a ring is uniformly distributed from 0 to 2π. The input dimension is 1 + 16 × 2 = 33. The ground-truth output activity has a similar structure to inputs and comprises of a 1D fixation and one ring output. The output dimension is thus 1 + 16 = 17. For preprocessing, we normalize the inputs to the range [0, 1]. These tasks are implemented in python module NeuroGym (https://neurogym.github.io/) based on the API of OpenAI Gym. Please refer to Yang et al.²⁷ for more details about how each task is set up.

Network training

During training, tasks are assumed to be learned sequentially. For the attention- guided behavior task, the training paradigm consists of three blocks with context 1, context 2 and context 1. Each block consists of 200 trials and there are 200 time steps within each trial. For cognitive tasks in Yang19 collection, we organize task trials into several blocks. Each block is considered as a temporal context and contains trials from a task. We use the last block to train the first learned task. Each block except the last one has 20000 trials. The last block has 10000 trials. We run the network on all possible task sequences and evaluate during training. In the simulation, the network has to solve either two or three tasks sequentially. For the two-task case, we use all 15 cognitive tasks. But for the three-task case, we randomly select 7 tasks out of 15 tasks (DNMS, DMC, Ctx DM 2, MultSen DM, Dly Anti, Go) to reduce the training time.

Model evaluation and comparison

A trial is considered correct when the model makes the same action as ground truth in the decision period. We evaluate the performance of each task every 500 trials during training. The number of evaluation trials is 30. We use mean accuracy of evaluation trials as model performance. We also define continual learning (CL) and forward transfer (FT) performance to measure forgetting and knowledge transfer, respectively. These two are defined in the two-task case. Particularly, CL performance is defined as the task 1 performance after training task 2 in block 2. FT performance is defined as task 2 performance after training task 1 in block 1.

We implement elastic weight consolidation (EWC) and synaptic intelligence (SI) as baseline models. We use grid search to find the hyperparameter set that has the best continual learning performance. We also knockout MD or both PFC-ctx and MD in the network as control. When knocking out MD alone, MD is bypassed and PFC-ctx is directly connected to PFC. We keep the effect of PFC-ctx to PFC the same as MD to PFC in the full model. First, we use the same way to initialize PFC-ctx to PFC weight (see Network structure and weight initialization). Second, PFC receives base-level inhibition. We also apply Winner-Take-All to PFC-ctx activity so that PFC-ctx can disinhibit part of PFC population. When knocking out both PFC-ctx and MD, the network does not have any context-relevant modules. It only consists of input layer, hidden RNN layer (PFC) and output layer.

Activity analysis in PFC area

In Fig. 5F, we compared the activity trajectory of PFC area in networks with and without MD. We record one trial activity from PFC area in both settings and visualize network trajectory with principal component analysis (PCA). PCA linearly reduces the dimensionality of neural activity to 2D space. In Supplementary Fig. 6, we further analyzed the representation in PFC area. Similar to trajectory analysis, we record activity of PFC area in networks with and without MD for multiple trials, and compute mean activity over trials. In the activity analysis, results are shown with task 1 = Dly Go and task 2 = DNMC. The task choice does not affect the conclusion.

Task similarity analysis

The task similarity is based on task representation in artificial neural network. We trained an single hidden layer RNN to solve 15 tasks in a interleaved way and analyze task representation with task variance analysis²⁷. Task variance of task A and a hidden unit i is defined as

$${tv}_{i}\left(A\right)={\left\langle {\left[{r}_{i}(\;j,t)-{\left\langle {r}_{i}(\;{j}^{{\prime} },t)\right\rangle }_{{j}^{{\prime} }}\right]}^{2}\right\rangle }_{j,t},$$

(29)

where r_i( j, t) is the activity of unit i on time t of trial j. Each task is then expressed as a representation vector consisting of task variance values of the hidden layer $TV\left(A\right)=\left(t{v}_{i}\left(A\right)\right)$. Each representation vector is normalized with Euclidean norm. We use inner product of normalized representation vectors of two tasks to measure the similarity.

$$\,{{\mbox{Similarity}}}\,\left(A,B\right)=\frac{TV\left(A\right)}{{\left\vert \left\vert TV\left(A\right)\right\vert \right\vert }_{2}}\cdot \frac{TV\left(B\right)}{{\left\vert \left\vert TV\left(B\right)\right\vert \right\vert }_{2}}.$$

(30)

The similarity value ranges from 0 to 1. For Fig. 7C, we define task pairs with similarity value higher than 0.5 as similar tasks. The rest task pairs are non-similar.

Varying MD to PFC projection

In Fig. 7, we enable forward transfer by reducing inhibition level and adding overlapping PFC neurons. In the original MD to PFC connections, every PFC neuron receives inhibition from MD and the inhibition level b is set to 5. But in the overlapping MD to PFC connections, only 10% randomly selected PFC neurons receives inhibition and b is set to 0.5.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.