Abstract
Detection and Dissection of Anomalous Tissue Domains (DDATD) from multi-sample spatial transcriptomics (ST) data provides unprecedented opportunities to characterize anomalous tissue domains (ATDs), revealing both population-level and individual-specific pathogenic factors for understanding pathogenic heterogeneities behind diseases. However, no current methods can perform de novo DDATD from ST data, especially in the multi-sample context. Here, we introduce STANDS, an innovative framework based on Generative Adversarial Networks which integrates three core tasks in multi-sample DDATD: detecting, aligning, and subtyping ATDs. STANDS incorporates multimodal-learning, transfer-learning, and style-transfer techniques to effectively address major challenges in multi-sample DDATD, including complications caused by unalignable ATDs, under-utilization of multimodal information, and scarcity of normal ST datasets necessary for comparative analysis. Extensive benchmarks from diverse datasets demonstrate STAND’s superiority in identifying both common and individual-specific ATDs and further dissecting them into biologically distinct subdomains. STANDS also provides clues to developing ATDs visually indistinguishable from surrounding normal tissues.
Similar content being viewed by others
Introduction
Detecting and characterizing biologically heterogeneous anomalous tissue domains (ATDs) from multiple tissue samples is of paramount importance in clinical diagnostics, targeted therapies and biomedical research1,2,3 (Fig. 1a). This procedure, which we refer to as Detection and Dissection of Anomalous Tissue Domains (DDATD), serves as the first and foremost step in a comprehensive analysis of tissues from affected individuals for revealing population-level and individual-specific factors (e.g., pathogenic cell types) associated with disease development.
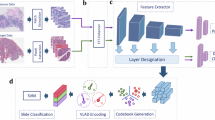
a Outline of DDATD. Given ST datasets collected from multiple affected individuals, DDATD first identifies their anomalous anatomical regions by referencing a ST or scRNA-seq dataset obtained from a control individual (e.g., a healthy individual). Next, these anomalous regions are processed to diminish their cross-individual non-biological variations (e.g., technical differences). Lastly, processed anomalous regions are further dissected into biologically distinct subtypes that are either common or individual-specific. These subtypes provide insights to heterogeneities of the disease both within and cross individuals and serve as potential targets for developing targeted therapies. b Framework of STANDS. The framework consists of three components (C1, C2 & C3) corresponding to the tasks of anomaly detection, alignment, and subtyping in DDATD. Initially, C1 utilizes a GAT and a GAT-ResNet hybrid network to yield gene expression and histology image embeddings respectively for each spatial spot. These embeddings are fused using a TF block to generate multimodal embeddings, which subsequently are fed to a GAN module (module I) aims at learning to reconstruct normal spatial spots in the reference dataset. The trained model is then applied to target datasets to identify anomalous spatial spots as those with largest reconstruction errors (or anomaly scores). C2 trains a GAN model (module II) to identify “kin” pairs of target and reference spots, based on which another GAN model (module III) learns a “style”-divergence matrix for aligning the target datasets within the reference data space via “style-transferring”. Anomalous spots identified by C1 are initially excluded from the training phase of C2 to diminish their confounding effects, and later aligned in the testing phase. Finally, C3 fuses the embeddings and reconstruction residuals of aligned anomalies to serve as inputs for an iterative clustering algorithm (DEC) for anomaly subtyping. Figure 1a created with some elements from smart.servier.com under a Creative Commons Attribution 4.0 International license (CC BY 4.0).
Traditionally, DDATD relies on either meticulous expert visual inspection or computer vision algorithms applied to histology images4,5. Spatial Transcriptomics (ST) provides an unprecedented opportunity to enhance DDATD by integrating spatial gene expression information across tissues.
Unlike the spatial clustering task frequently encountered in ST, which focuses on clustering spatial spots into spatial domains6,7,8,9,10, DDATD necessitates further isolation of anomalous clusters from normal ones. Existing methods developed for spatial clustering either fail to identify anomalous clusters (e.g., SpaGCN6 and GraphST11) or rely on “expert-defined” anomaly markers (e.g., cancer gene signatures in iStar9, TESLA12, and cell2location13). However, such markers are frequently unavailable, especially for under-researched or novel domain types, severely constraining the applicability of spatial clustering methods in de novo DDATD. Currently, Spatial-ID14 is the sole available marker-free, spatial clustering method capable of distinguishing anomalous spatial spots from normal ones. However, its presents significant shortcomings, including its reliance on annotated reference scRNA-seq data of the target tissue, which is not always available, a high false-positive rate stemming from confusing normal spots of uncertain assignments with bona fide anomalies15, and challenges in handling multiple target datasets due to the lack of cross-sample ST alignment mechanisms. To our knowledge, no existing computational methods can perform de novo, annotated-reference-free DDATD from ST data, especially in the context of multiple samples.
The de novo DDATD workflow for multi-sample ST comprises three sequential core tasks: detecting ATDs, aligning them across multiple samples, and classifying them into shared or sample-specific types. Several computational challenges impede these tasks. First, batch effects can compromise the accuracy of anomaly detection16,17, thus necessitating a preliminary multi-sample alignment for batch correction. However, anomalies themselves can complicate this alignment process15,18, reducing the effectiveness of batch correction. Additionally, existing methods fall short of aligning multiple ST samples within a unified space that maintains the data’s original scale and semantic integrity19, thus hampering both the interpretation of aligned data and its utilization in subsequent tasks, such as anomaly subtyping. Furthermore, the scarcity of “normal” reference ST datasets hampers DDATD, as the definition of “anomaly” relies on the comparison with “normal”. Although ST datasets derived from healthy human tissues are being continually added to public databases such as HubMap20 and STOmicsDB21, they are limited in quantity and tissue types, given acquiring healthy tissues presents significant challenges, particularly for tissues of vital organs. Moreover, the lack of effective methods to integrate multimodal signals from both spatial gene expression data and histology images severely restricts the potential of DDATD analysis. Finally, integrating the three sequential tasks into a methodologically coherent framework, rather than simply combining individual methods specifically designed for each task, is vital to ensure their collective effectiveness.
To address these challenges, we introduce Spatial Transcriptomics ANomaly Detection and Subtyping (STANDS), an innovative framework built on a suite of specialized Generative Adversarial Networks (GANs) for seamlessly integrating the three core tasks of DDATD. The framework consists of three components, each dedicated to one of the core tasks of DDATD (Methods and Fig. 1b). Component I (C1) trains a GAN model on the reference dataset, learning to reconstruct normal spots from their multimodal representations of both spatial transcriptomics data and the associated histology image patches22. Subsequently, the model is applied on the target datasets to identify anomalous spots as those with unexpectedly large reconstruction deviances, namely anomaly scores23. As nonbiological variations (e.g. batch effects) potentially complicate anomaly subtyping, Component II (C2) employs two cooperative GAN models to diminish them via “style-transferring” target datasets into a common space, while preserving the data’s original scale and semantic integrity24. Component III (C3) fuses the embeddings and reconstruction residuals of aligned anomalous spots to serve as inputs to a self-paced clustering algorithm25 which groups anomalies into biologically distinct subtypes. STANDS is extensively benchmarked in a series of experiments that are deliberately designed for the three core tasks of DDATD under various scenarios (Table 1). These experiments involve datasets spanning a diverse range of platforms, tissues, and species (Supplementary Table 1). Compared to benchmark methods (Supplementary Table 2), our method demonstrates unparalleled performances across these experiments in identifying both nascent and developed ATDs from single and multiple ST samples, aligning ST samples, whether adjacent or non-adjacent, to diminish nonbiological variations among ATDs, and dissecting ATDs into biologically distinct subdomains that can be either shared across samples or unique to individual samples. Notably, STANDS remains effective even using scRNA-seq datasets as surrogate references, and its performance is not compromised when dealing with multiple samples with unalignable sample-specific ATDs. In addition to STANDS, we also introduce Spatial Grouping Discrepancy (SGD) as a novel metric to evaluate the spatial organization of detected ATD subdomains (see “Evaluation metrics” section in Methods). In contrast to conventional clustering metrics like accuracy and Adjusted Rand Index (ARI), which treat observations as equal-weighted and independent, SGD pioneers in incorporating spatial relationships among spots into the evaluation and thus are particularly suited for assessing spatial clustering results in ST analyses.
Results
Overview of STANDS
STANDS is a suite of GAN modules specialized for integrating and fulfilling three core tasks of DDATD from multi-sample ST: detecting, aligning, and subtyping of ATDs. For ease of discussion, we will refer to observations in ST datasets as “spots” regardless of their resolutions, and to spots within reference and target datasets as reference and target spots, respectively. Moreover, the term “dataset” is used interchangeably with “sample”, the phrase “adjacent datasets” refers to datasets obtained from vertically sliced tissue samples, while “non-adjacent datasets” are derived from noncontiguous samples of the same tissue type but different donors.
The fundamental idea behind STANDS is that a GAN model can learn either the “content” (biological) variations between normal and anomalous regions or the “style” (batch) variations across ST datasets. The workflow of STANDS is structured into three components, each corresponding to one of the aforementioned three tasks (Fig. 1b). Component I (C1) is dedicated to detecting ATDs in target datasets (see “Anomalous tissue region detection” section in Methods). It involves a GAN module (module I), which is trained on the reference dataset to reconstruct normal spots accurately. Trained module I is then applied on target datasets to identify anomalous spots as those exhibiting substantial reconstruction deviances (or anomaly scores), given that module I has been trained exclusively on normal data. Crucially, this approach remains effective despite potential batch variations, as anomalies consistently exhibit higher anomaly scores relative to normal spots. The reconstruction is based on spots’ latent multimodal embeddings from module I’s encoder, which employs a graph attention (GAT) network and a ResNet-GAT hybrid network to learn the latent representations of gene expression and histology images for each spot. These two embeddings are then fused using a transformer fusion (TF) block22 to generate a multimodal embedding (see “Multimodal learning of spatial gene expression data and histology image” section in Methods). In scenarios where a normal ST dataset is unavailable, the encoder employs a multi-layer perceptron (MLP) network to utilize normal scRNA data as surrogate reference and treat spatial spots in target dataset as single-cells to generate their embeddings.
Component II (C2) utilizes the spot embeddings generated by C1 to align target datasets in the reference data space (see “Multi-sample ST data alignment” section in Methods). Initially, identified anomalous spots from component I are excluded from target datasets to eliminate their confounding effects. Two GAN modules, module II &III, work in tandem in this component. Module II creates “kin” pairs between reference and target spots by learning a non-negative mapping matrix \({{\bf{M}}}\in {{\mathbb{R}}}^{{N}_{T}\times {N}_{R}}\), where \({N}_{T}\) and \({N}_{R}\) denote the number of target and reference spots, respectively. Subsequently, module III utilizes these “kin” pairs to learn a “style”-divergence matrix \({{\bf{S}}}\in {{\mathbb{R}}}^{{N}_{{batch}}\times d}\), based on which the target datasets are “style”-transferred to the reference dataset’s “style” space, thereby diminishing their batch variations.
Component III (C3) aims to group anomalous spots into biologically distinct tissue subdomains through a clustering process (see “Subtyping anomalous tissue domains across multiple datasets” section in Methods). Specifically, the C1-generated embeddings and reconstruction residuals of aligned anomalous spots are fused by a TF block to serve as inputs for the discriminatively boosted clustering algorithm, DEC. This algorithm iteratively refines anomalies’ embeddings and cluster centroids, incrementally transforming harder-to-cluster anomalies into easier ones until either a predetermined number of iterations is reached, or the cluster assignment change between two successive iterations falls below a prespecified threshold.
STANDS identifies cancerous domains in single human breast cancer ST dataset
Initially, we leverage STANDS to identify carcinogenic domains within human breast cancer tissues. Specifically, this experiment (Exp ID = 1 in Table 1) involves a 10x Visium reference dataset (10x-hNB-v05), which is prepared from healthy human breast tissues and encompasses four normal domain types, and a 10x Visium target dataset (10x-hBC-G2), which is derived from human breast cancer tissues and encompasses two additional carcinogenic domain types including the cancer in situ (CIS) and the invasive cancer (IC) domains. As benchmarks, we include Spatial-ID, the sole available marker-free method for ATD detection in ST, along with four methods—CAMLU15, scPred26, CHETAH27, and scmap28 — originally developed for anomaly detection in scRNA-seq, all of which treat spatial spots as single-cells.
STANDS significantly outperforms the competing methods in correctly identifying spots within the carcinogenic domains in terms of accuracy, F1-score, Precision-Recall (PR) curve, and SGD scores (Fig. 2a, b). Here, a lower SGD score indicates the corresponding result is more spatially consistent with the ground truth (see “Evaluation metrics” section in Methods). Furthermore, the legitimacy of using STANDS’ anomaly scores for identifying ATDs is evident from the bimodal distribution of the normalized anomaly scores in the target dataset, which clearly separates anomalous and normal spots (Fig. 2c, lower panel). Intriguingly, normal spots in closer proximity to anomalous regions tend to have higher anomaly scores (Fig. 2c, top panel). We postulate that these normal-looking spots may be pathologically relevant. To verify this, we examine normal spots with high anomaly scores, which STANDS falsely identifies as anomalies. Many of these spots are adjacent to carcinogenic regions and may represent emerging cancerous areas (Fig. 2c, middle panel). Such areas are visually indistinguishable from the surrounding “normal” tissues in the histology image (Fig. 2d) but exhibit substantially elevated expression levels of breast cancer marker genes (e.g., ACTB29 &TMSB1030, Fig. 2e). Therefore, these false positive anomalies are clinically significant as they provide insights into the tumor developmental trajectories. Finally, we repeat this experiment using Slide-seqV2 datasets (Exp ID = 4), where two mouse embryo datasets are selected as the reference (ssq-mEmb-32) and target (ssq-mEmb-33) datasets, respectively. The domains of cardiac valve (CV) cells and neuroectodermal (NED) cells are designated as ATDs in the target dataset and excluded from the reference dataset. Not surprisingly, STANDS surpasses the benchmark methods in accurately distinguishing CV and NED domains from others (Supplementary Fig. 1).
a Identification of ATDs in a 10x Visium human breast cancer dataset. True anomalous spots and those identified by the tested methods are both indicated in blue in the ground truth and respective method panels. b Performances of the tested methods are quantified using accuracies and F1-scores, PR curves, SGD_degree and SGD_cc scores. Accuracies and F1-scores are calculated in 5 independent experiments and presented as mean ± SD. c Top scatter plot maps each spot’s distance to the nearest carcinogenic region (x-axis) against its anomaly score (y-axis). Spots in the green circle are true anomalies. Yellow spots denote STANDS-identified anomalies. Red line is a regression line representing the correlation between anomaly scores and distances. Middle spatial map shows the spatial distribution of anomaly scores, with a color gradient from blue to red indicating lower to higher scores. Bottom histogram illustrates the probability density distributions of normalized anomaly scores in the reference and target datasets. d STANDS pinpoints emerging cancers adjacent to known cancerous regions. Spots within cancerous regions are in red, while those within normal tissue regions are in cyan. Notably, normal spots in orange, which are adjacent to cancerous regions and identified as anomalies, potentially represent developing cancer. e Expression levels of breast cancer marker genes ACTB and TMSB10 within the normal (n = 238), emerging cancerous (n = 69), and known cancerous regions (n = 160). In the boxplot, the center line denotes the median, box limits denote the upper and lower quartiles, and whiskers denote the 1.5× interquartile range. f Cross-modality identification of ATDs within a 10x Visium pancreatic ductal adenocarcinomas dataset, using a healthy pancreatic duct scRNA-seq dataset as reference. True anomalous spots and those identified by the tested methods are both indicated in green in the ground truth and respective method panels. g Performances of the tested methods are quantified using accuracy and F1-scores, PR curve, and a scatterplot of SGD_degree vs SGD_cc scores. Accuracies and F1-scores are also calculated in 5 independent experiments and presented as mean ± SD. Source data are provided in this paper.
STANDS concurrently identifies anomalous tissue domains across multiple ST datasets
We then evaluate STANDS’ performance in concurrently detecting ATDs across multiple ST samples derived from different donors. This evaluation (Exp ID = 3) involves the 10x-hNB-v05 dataset as the reference and two 10x Visium human breast cancer datasets (10x-hBC-H1 and 10x-hBC-G2) as the targets. We challenge STANDS by curating the target datasets to encompass both shared and dataset-specific ATDs: the IC domain is shared across datasets, while the CIS and adipose tissue (AT) domains are unique to 10x-hBC-G2 and 10x-hBC-H1, respectively. Additionally, we continue with the same four benchmark methods employed in the preceding section. As shown in Fig. 3, STANDS is the only method that accurately delineates ATDs in spatial maps of both target datasets. In contrast, Spatial-ID can only demarcate the AT domain, CAMLU almost entirely fails to identify any anomalies, scPred and CHETAH tend to identify anomalies dispersed throughout the tissues, and scmap mistakenly categorizes most spots as anomalous. STANDS’ superiority is further quantitatively substantiated by its better accuracy, F1-score, and Precision-Recall (PR) curve results, compared to those of the benchmark methods. Furthermore, as detailed in Table 1 (Exp ID = 5-8) and Supplementary Note 1.1, this evaluation is extensively repeated across datasets of diverse platforms, tissue types, and health states, including the mouse embryo Slide-seqV2 (ssq-mEmb) and Stereo-seq (stereo-mEmb) datasets, the human primary sclerosing cholangitis 10x Visium datasets (10x-hPSC), as well as the human renal cell cancer 10x Visium datasets (10x-hRCC). Supplementary Figs. 1–5 consistently demonstrate that, compared to the benchmarks, STANDS excels in concurrently identifying biologically heterogeneous ATDs from multiple target datasets.
a, Identification of ATDs across two 10x Visium human breast cancer datasets (10x-hBC-G2 and 10x-hBC-H1). As shown in the original spatial maps on the upper-left corner, the two datasets encompass both common (IC, indicated in cyan) and unique (CIS in 10x-hBC-G2, indicated in orange; adipose tissue (AT) in 10x-hBC-H1, indicated in deep blue) ATDs. These ATDs are collectively indicated in light blue in the ground truth panel. The anomalous spots identified by STANDS and five benchmark methods are indicated in light blue in their respective panels. b, Performances of the tested methods are quantified and visualized using a bar plot of their accuracies and F1-scores, a plot of PR curves, and a scatter plot of their SGD_degree and SGD_cc scores. And accuracies and F1-scores are calculated in 5 independent experiments and presented as mean ± SD. Source data are provided in this paper.
STANDS identifies pancreatic cancerous domains via cross-referencing pancreatic scRNA-seq data
The scarcity of normal ST datasets from healthy individuals, which serve as comparative baselines, presents a primary challenge in detecting ATDs from diseased ST datasets. STANDS innovatively circumvents this limitation by transferring knowledge from more accessible normal scRNA-seq datasets of the same tissue type. To assess STANDS’ performance in this cross-modal anomaly detection, we use a normal scRNA-seq dataset derived from healthy human pancreatic ductal tissues as a surrogate reference. The target dataset is a 10x Visium dataset (10x-hPDAC) prepared from pancreatic ductal adenocarcinomas (PDAC), with cancerous domains designated as anomalous. Recognizing that researchers often resort to using unsupervised anomaly detection methods in the absence of suitable reference datasets, we expand our benchmarking to include SCEVAN31 and CopyKAT32, two unsupervised methods developed for detecting tumor cells from scRNA-seq data, alongside the five supervised benchmark methods in earlier sections. As shown in Fig. 2f, STANDS successfully delineates the primary carcinogenic region on the spatial map, outperforming all benchmark methods that either mark only sporadic cancer spots or erroneously label most spots as anomalous. This superiority is corroborated by STANDS’ highest accuracy and F1-scores as well as its lowest SGD scores (Fig. 2g).
STANDS effectively aligns multiple ST datasets sharing identical domain types
This section evaluates STANDS’ effectiveness in aligning multiple ST datasets without the interference of unalignable, dataset-specific domain types. This evaluation begins with a simple scenario (Exp ID = 13) involving aligning multiple vertical human PSC 10x Visium datasets (10x-hPSC-A1, C1, and D1). The second scenario (Exp ID = 9) is more involved as we aim to align three non-adjacent 10x Visium healthy human breast tissue datasets (10x-hNB-v05, 10x-hNB-v06, and 10x-hNB-v07). The benchmark methods include Harmony33 and ComBat34, originally designed for scRNA-seq data integration, as well as GraphST11 and STAligner35, designed for aligning ST datasets.
The results of the first and second scenarios are displayed in Fig. 4 and Supplementary Fig. 6, respectively. UMAPs in Fig. 4a and Supplementary Fig. 6a demonstrate that STANDS surpasses most benchmark methods in intermingling data and maintaining accurate domain type alignment across datasets. This superiority is supported by metrics that measure the batch mixing effects (iLISI, BatchKL, and ASW_batch, see Methods) and the accuracy of cross-batch domain type alignment (ASW_type), as shown in Fig. 4b and Supplementary Fig. 6b. To further assess the effectiveness of multi-sample alignment, we utilize GraphST for joint spatial domain clustering, which is a natural and important downstream task, on the aligned datasets in both scenarios. For establishing baseline results, we also perform joint spatial clustering on the unaligned datasets. The annotated spatial maps in Fig. 4c and Supplementary Fig. 6c illustrate that, although GraphST achieves improved spatial domain clustering results for all post-alignment datasets relative to the baseline results, the most accurate results are observed for STANDS-aligned datasets, as evidenced by STANDS’ highest joint ARI score shown in Fig. 4d and Supplementary Fig. 6d.
a Three vertical PSC datasets (10x-hPSC-A1, -C1, and -D1) aligned by STANDS and four benchmark methods are visualized in their two-dimensional UMAPs. UMAPs in the first row showcase the batch mixing effects, wherein spots in blue, orange, and green originate from 10x-hPSC-A1, -C1, and -D1, respectively. UMAPs in the second row exhibit the cross-batch domain type alignment, with each domain type represented by a unique color. b The batch mixing effects are measured using iLISI and BatchKL metrics, illustrated in the left-hand scatterplot with larger values in both metrics signifying better batch mixing. The right-hand radar plot represents an integrated view of methods’ efficacies in batch mixing and domain type alignment, which are positively correlated with the 1-ASW_batch and ASW_type scores, respectively. c GraphST is utilized to perform joint spatial clustering across the three datasets aligned by the tested methods. Additionally, the joint spatial clustering results across unaligned datasets are also provided as a baseline (second column). The clustering results are illustrated on spatial maps of the three datasets. d The bar plot illustrates the ARI scores for the joint spatial clustering results from Fig. 4c. Source data are provided in this paper.
We repeat this experiment using multiple vertical human breast cancer 10x Visium datasets (Exp ID = 13, Supplementary Fig. 7), non-adjacent mouse embryo Slide-seqV2 (Exp ID = 12, Supplementary Fig. 8) and Stereo-seq (Exp ID = 14, Supplementary Fig. 9) datasets. It is worth mentioning that, to increase the challenge of the first scenario (Exp ID = 13), we select three vertical slices (10x-hBC-A1, 10x-hBC-A4, and 10x-hBC-A6) from a collection of six 10x Visium human breast cancer datasets (10x-hBC-A1 to A6) so that their inter-slice z-axis distance a maximized. Given that adjacent 10x-hBC datasets are 32 μm apart along the z-axis, our selection achieves a minimum z-axis distance of 32×2 = 64μm between A4 and A6 and a maximum distance of 32×5 = 160μm between A1 and A6. Generally, these experiments demonstrate results similar to those in Fig. 4 and Supplementary Fig. 6, except that, in Supplementary Fig. 7a, Harmony appears to better separate immune infiltrates from other domain types in the post-alignment data compared to STANDS, contradicting with the metric results (Supplementary Fig. 7b and d). This observation can be explained by the small proportion of immune infiltrates, whose well-separation has limited impact on overall type alignment. STANDS, on the other hand, excels in separating major domain types such as breast glands, adipose tissues, and connective tissues. This is evidenced by the ASW_type metric in the right panel of Supplementary Fig. 7b, which assesses cross-batch type alignment. STANDS has a higher ASW_type score (0.52) compared to Harmony (0.5), indicating a slightly advantage in separating cell types in mixed batches. Additionally, Supplementary Fig. 7d shows that data aligned by STANDS (ARI = 0.24) achieves better spatial clustering performance than data aligned by Harmony (ARI = 0.23). Finally, these findings altogether highlight STAND’s remarkable ability not only in effectively integrating multiple ST datasets but also in ensuring their accurate domain alignment, irrespective whether the datasets are adjacent or non-adjacent.
STANDS effectively aligns multiple ST datasets with non-overlapping domain types
In this section, we aim to align datasets with both shared and unique domain types. This scenario is not only more realistic for ADT analysis in multi-sample ST, but also presents greater challenges since the biological variations arising from inconsistent domain types can confound with nonbiological variations, thus complicating the data alignment. Our experiment (Exp ID = 10) involves a normal breast tissue dataset (10x-hNB-v07) and two breast cancer datasets (10x-hBC-G2 &10x-hBC-H1) that have been curated to share all domain types, except for the CIS and IC domains that are unique to 10x-hBC-G2 and 10x-hBC-H1, respectively. The benchmark methods include Harmony, ComBat, STAligner, and GraphST. As shown in Fig. 5a, STANDS is the sole method that not only achieves superior batch integration but also successfully separates the two dataset-specific domains (CIS and IC) from regions common to all datasets and avoids their intermingling with each other. To systematically evaluate the impacts of dataset-specific domains, we compare the effectiveness of multi-sample alignment in the presence versus absence of dataset-specific domains. The latter condition is created by excluding both CIS and IC domains from the two cancerous datasets. As shown in Fig. 5b, STANDS not only significantly outperforms all benchmark methods in both batch mixing and domain type alignment, as evidenced by its superior iLISI, BatchKL, ASW_batch, and ASW_type scores, but also stands out as the only method whose effectiveness remains robust to the dataset-specific domain types. Moreover, as shown in Fig. 5c, d, GraphST yields the most accurate joint spatial clustering results using datasets aligned by STANDS, further demonstrating that STANDS excels in diminishing non-biological variations across datasets. Such an observation can be attributed to both the effective mitigation of batch effects and the enhancement of domain-relevant gene expression patterns in STANDS-aligned datasets. For instance, IRF6 and SLCA40A1 genes, known to be implicated in AT function and immune metabolism respectively36,37, exhibit elevated expression levels within the AT and immune infiltrates domains in the normal 10x-hNB-v07 dataset. Although such expression patterns are subdued in the original 10x-hBC-G2 and 10x-hBC-H1 datasets, they become more pronounced following STANDS’ alignment (Fig. 6).
This analysis involves three datasets, including 10x hNB-v07, 10x-hBC-G2 and 10x-hBC-H1. The CIS and IC domains are unique to 10x-hBC-H1 and 10x-hBC-G2, respectively. a Datasets aligned by STANDS and four benchmark methods are visualized in their two-dimensional UMAPs. UMAPs in the first row showcase the batch mixing effects, wherein spots in yellow, blue, and red originate from 10x hNB-v07, 10x-hBC-G2 and 10x-hBC-H1, respectively. UMAPs in the second row exhibit the domain type alignment, with domain types indicated in different colors. Particularly, in STANDS’ panel, the CIS (in cyan) and IC (in brown) domains are enclosed by a red circle. b The ASW_type vs 1-ASW_batch scatterplot provides a dual assessment of the methods’ efficacies in both domain type alignment and batch mixing, while also showcasing the impacts of dataset-specific domains, with their presence indicated in yellow and absence indicated in green. Similarly, the iLISI vs BatchKL scatterplot illustrates the methods’ efficacies in batch mixing in the presence or absence of dataset-specific domains. c GraphST is utilized to perform joint spatial clustering across the three datasets aligned by the tested methods. Additionally, the joint spatial clustering results across unaligned datasets are also provided as a baseline (second column). The clustering results are illustrated on spatial maps of the three datasets. d The bar plot illustrates the ARI scores for the joint spatial clustering results from Fig. 5c. Source data are provided in this paper.
a The spatial expression levels of adipose tissue (AT)-relevant IRF6 gene across tissues are depicted on spatial maps of the three datasets before (the second column) and after (the third column) the alignment by STANDS. The regions encompassed by red rectangles correspond to the AT domains. The first column showcases the ground truth domain labels on the spatial maps. The rightmost two columns depict the spatial expression levels of immune infiltrates-related SLC40A1 gene. The regions encompassing the immune infiltrates domains are enclosed by red rectangles in panels of the two columns. In all columns after the first one, a red shifted color signifies a higher gene expression level. b Heatmaps on the left show the expression levels of IRF6 and SLC40A1 genes across various tissue domains before (left panel) and after (right panel) the alignment by STANDS. The violin plot on the right shows the distribution of log expression values of IRF6 and SLC40A1 across the adipose tissue (n = 210) and immune infiltrates (n = 40) domains respectively, both before (red) and after (blue) the alignment by STANDS. For the box in violin plot, the white dot denotes the median, box limits denote the upper and lower quartiles, and whiskers denote the 1.5× interquartile range. Source data are provided in this paper.
STANDS discerns biologically distinct anomalous tissue subdomains in single ST datasets
Subtyping ATDs in single target datasets represents the most fundamental task for discerning biologically distinct subdomains, as the ATDs are devoid of batch variations. We assess the performances of STANDS in this context using the 10x-hBC-G2 (Exp ID = 18) and 10x-hBC-H1 (Exp ID = 19) datasets, respectively. The CIS and IC domains in 10x-hBC-G2, and the AT and IC domains in 10x-hBC-H1 have been curated as anomalous. Given the accuracy of anomaly subtyping is contingent upon the outcomes of anomaly detection, the benchmark methods are composite methods, which are simple combinations of individual methods specialized for anomaly detection and subtyping. These include the five supervised benchmark methods for anomaly detection (Spatial-ID, CAMLU, scPred, CHETAH, and scmap), coupled with a spatial clustering method—GraphST, STAGATE, or iStar—for grouping identified ATDs into distinct subdomains, yielding six composite benchmark methods: scmap-GraphST, CAMLU-GraphST, CHETAH-GraphST, scPred-GraphST, SpatialID-STAGATE, and SpatialID-iStar. As shown in Supplementary Fig. 10, STANDS consistently outperforms the benchmark methods in generating ATD subtype labels that closely align with the ground truth in annotated spatial maps, as quantitatively evidenced by its highest Macro-F1 and NMI scores. Note that NMI scores are computed on true positive anomalous spots identified by each method, while Macro-F1-scores are on true positives, false positives, and false negatives. Supplementary Fig. 11 showcases that STANDS’ superiority remains when this experiment is extended to using single Slide-seqV2 datasets (Exp ID = 20 and 21).
STANDS discerns biologically distinct anomalous tissue subdomains across multiple ST datasets
In the final assessment, we examine STANDS’ ability to concurrently discern biologically distinct subdomains within ATDs across multiple datasets. The benchmark methods include the same six composite methods as in the preceding section, with the addition of STAligner to SpatialID-STAGATE, ComBat to SpatialID-iStar, and GraphST to the other four methods for aligning cross-dataset ATDs (see “Benchmark implementations” in Methods). This experiment comprises two scenarios involving two 10x Visium target datasets (10x-hBC-G2 & 10x-hBC-H1). In the first scenario (Exp ID = 16, Supplementary Fig. 12), both datasets share identical ATD subdomains (IC &CIS), while in the second scenario (Exp ID = 15, Fig. 7), they have been curated to include both overlapping (CIS) and unique (IC in 10x-hBC-G2; AT in 10x-hBC-H1) ATD subdomains. In both scenarios, ATD subdomains delineated by STANDS closely align with the ground truth in the annotated spatial maps and Sankey plots (Supplementary Fig. 12a, b and Fig. 7a, b). Conversely, the benchmark methods struggle with correctly distinguishing ATD subdomains, especially those shared between datasets. For example, spots within the CIS subdomain are either overlooked (e.g., CAMLU-GraphST) or misclassified as distinct subdomains (e.g., scmap-GraphST). Supplementary Fig. 12c and Fig. 7c quantitatively demonstrate STANDS’ superiority over the benchmark methods in terms of Macro-F1, NMI, and multi-SGD scores. It is worth mentioning that NMI scores are computed on true positive anomalous spots identified by each method, Macro-F1 on all iden- and multi-SGD scores are on true positives, false positives and false negatives. Additionally, the cells along the leading diagonals of heatmaps of Supplementary Fig. 12d and Fig. 7d represent the spatially optimal matches between the predicted subdomain labels and the ground truth, determined using the multi-SGD scores (see “Evaluation metrics” section in Methods). The cell color intensity indicates the degree of spatial consistency between the matched label pairs. STANDS exhibits the most pronounced patterns along these diagonals, signifying that its subtyping results consistently achieve the best spatial matching with the ground truth. We still test STANDS and benchmark methods’ performance on Stereo-seq datasets (Exp ID = 23, Fig. 8), which share identical ATD subdomains (branchial arch & primitive gut tube). The spatial plots (Fig. 8a) and metrics (Fig. 8c, d) show the advantages of STANDS compared with the benchmark methods on Stereo-seq data. To assess STANDS’ generalizability, we further conduct a series of experiments (Exp ID = 17, 22, 24) using the ATDs identified from the three experiments (Exp ID = 5, 6, 8) in Supplementary Note 1.1, where ST datasets spanning across diverse platforms, tissue types, and health states are involved. The experimental settings and results of these experiments are detailed in Supplementary Note 1.2. Briefly, compared to the benchmarks, STANDS not only excels in accurately detecting ATDs and dissecting them into biologically distinct subdomains, but also in recognizing them as either shared by target datasets or unique to specific ones.
a The ATDs include the CIS, IC, and adipose tissue (AT) subtypes. As shown in the ground truth panel of spatial maps, the CIS (in orange) domain is shared between the two experimental datasets (10x-hBC-H1 and 10x-hBC-G2), while the IC (in green) and AT (in red) domains are unique to 10x-hBC-G2 and 10x-hBC-H1, respectively. Each of the tested methods (STANDS and six benchmark methods) sequentially identifies, aligns, and subtypes anomalous spots, with subtypes indicated in orange (CIS), green (IC) and red (AT) in methods’ respective panels of spatial maps. b Sankey diagrams detail the correspondence between the ground truth and the anomaly subtyping results from Fig. 7a. c The left scatterplot illustrates the Macro-F1 (y-axis) vs NMI (x-axis) scores of the methods in identifying and subtyping anomalous spots, respectively. The right scatterplot illustrates methods’ multi-SGD_degree (x-axis) vs multi-SGD_cc (y-axis) scores. Lower scores in both multi-SGD metrics indicate not only more accurate labeling but also that the subtyping results are more consistent with the ground truth in their spatial arrangement (see “Evaluation metrics” section in Methods). d The heatmaps of multi-SGD_degree (top row) and multi-SGD_cc (bottom row) scores of the methods. In each heatmap, the color intensity of cell \({c}_{i,j}\) inversely correlates with the SGD score (either degree or cc) calculated with the presumption that the method-generated subtype \(j\) corresponds to the true subtype \(i\). Cells on the leading diagonal indicate the optimal correspondence between the method’s subtyping results and the true subdomain labels (see “Evaluation metrics” section in Methods). Therefore, a more pronounced color pattern along a heatmap’s leading diagonal signifies more accurate subtyping. Source data are provided in this paper.
a As shown in the ground truth panel of spatial maps, the two target datasets (Stereo-mEmb-S1 and Stereo-mEmb-S3) share identical ATDs, including the branchial arch (in red) and primitive gut tube (in blue) domains. Each of the tested methods (STANDS and five benchmark methods) identifies, algins and subtypes anomalous spots, with subtypes indicated in red (branchial arch) and blue (primitive gut tube) in methods’ respective panels of spatial maps. b Sankey diagrams detail the correspondence between the ground truth and the anomaly subtyping results from Fig. 8a. c The upper scatterplot illustrates the Macro-F1 (y-axis) vs NMI (x-axis) scores of the methods in identifying and subtyping anomalous spots, respectively. The bottom scatterplot illustrates methods’ multi-SGD_degree (x-axis) vs multi-SGD_cc (y-axis) scores. d The cells on the leading diagonal in heatmaps of multi-SGD_degree (top row) and multi-SGD_cc (bottom row) scores illustrate the optimal correspondences between methods’ subtyping results and the true subdomain labels. A more pronounced color pattern along a heatmap’s leading diagonal signifies more accurate subtyping. Refer to Fig. 7 and the “Evaluation metrics” section in Methods for details. Source data are provided in this paper.
The impacts of reference diversity and size on STANDS’ performance
Recognizing the important roles of diversity and quantity of normal spots in the reference dataset for training STANDS, we systematically evaluate these factors using a healthy human breast 10x Visium dataset (i.e., 10x-hNB-v05) as the reference and a breast cancer 10x Visium dataset (i.e., 10x-hBC-G2) as the target. For the quantity evaluation, we conduct three experiments where we incrementally exclude one-third of the connective tissue spots from the reference dataset, as shown in Fig. 9a. We observe a decline in ATD detection accuracy during inference with fewer reference spots, as evidenced by lower AUC scores, F1-score, and an increased number of false positives (the left two bar groups in Fig. 9c). Notably, many new false positives appear in the connective tissue domains—14 spots (no removal), 20 spots (one-third removal), and 35 spots (two-third removal) as shown by the rightmost bar group in Fig. 9c. These findings demonstrate that reducing the number of reference spots of a specific domain type most significantly impacts the detection accuracy of the same type in the target dataset.
a–c demonstrate the impact of spot quantity in the connective tissue domains on STANDS’ performance in detecting cancerous regions in the breast cancer target dataset (10x-hBC-G2). a The left panel exhibits the connective tissue domains in the spatial map of the healthy breast tissue reference dataset (10x-hNB-v05). The right panel shows the incremental removal of one-third of the connective tissue spots ( ~ 415) from the reference dataset, as highlighted in different colors. b The spatial map in the upper row shows the ground truth domain annotations. The leftmost spatial map in the lower row shows the ground truth anomalous spots (in yellow). Other spatial maps in the lower row display STANDS-identified anomalous spots (in yellow and red), with red spots representing false positives in the connective tissue domains. c displays the performance changes as the number of connective tissue spots in the reference dataset decreases. The left two bar groups present STANDS’ performance metrics (AUC scores and F1-scores) on the left y-axis, while the rightmost bar group shows the total number of false positives on the right y-axis. In d–f, the impact of reference heterogeneity on STANDS’ performance in ATD detection is evaluated. d The left spatial map displays the ground truth domain annotations in the reference dataset. The middle and right spatial maps show the average cosine similarity of removed spots in immune infiltrates and breast glands domains, respectively, with the other spots. The average cosine similarity is represented by a color spectrum, with red indicating lower similarity and blue higher similarity. The average similarity of a domain type is also noted above its spatial map. e displays changes in STANDS’ performance in detecting anomalous target spots after removing immune infiltrates or breast glands from the reference dataset. f showcases the changes in STANDS’ false positive rate for target spots of immune infiltrates or breast glands following their respective removal from the reference dataset. Source data are provided in this paper.
For the diversity evaluation, we perform two experiments where spots within the immune infiltrate domains or an equal number of spots within the breast gland domains are excluded from the reference dataset. Compared to the breast glands, immune infiltrates are more similar to other normal domains in terms of average cosine similarities in gene expressions (Fig. 9d). Thus, the removal of breast glands decreases the level of reference diversity more significantly compared to immune infiltrates. Figure 9e shows that the removal of either domain type reduces STANDS’ overall ATD detection accuracy. Particularly, Fig. 9f shows that the removal of breast glands leads to a larger increase ( ~ 3.30 fold) in false positives for breast glands domains, compared to the removal of immune infiltrates ( ~ 2.94 fold). This can be explained by the fact that the information loss from removing immune infiltrates is better compensated by the remaining domain types during training. Consequently, STANDS learns less effective reconstruction of breast glands than immune infiltrates, leading to larger reconstruction errors and a higher false positive rate during inference. In summary, our findings indicate that a larger quantity of spots for a normal domain type during training reduces STANDS’ misclassification likelihood for that domain type during inference. Meanwhile, decreased reference diversity increases the misclassification likelihood for normal domain types missing in the reference dataset.
Ablation study
Here, we conduct a series of ablation studies on STANDS’ key model components to evaluate their impacts on performance for each subtask. The 10x-hNB-v05 dataset is used as the reference and the 10x-hBC-G2 dataset as the target for analyzing components in Components I (i.e., ATD detection) and III (i.e., ATD subtyping), while the 10x-hBC-A1, -A4, and -A6 datasets are used for Component II (i.e., multi-sample alignment). Model components involved in the ablation studies include the memory bank within the generator of GAN module I, the utilization histology data in ATD detection and subtyping, the TF blocks in STANDS’ Components I and III, and the nonnegative mapping matrix for multi-sample alignment.
Removing the memory bank leads to lower ATD detection accuracy (Supplementary Fig. 16a) and reduced variability in the training losses of both the generator and discriminator of GAN module I, especially in the later training phase where the discriminator’s loss becomes lower while the generator’s loss becomes higher without further improvement (Supplementary Fig. 16b). This loss pattern indicates a tendency towards mode collapse, a frequent cause to GAN’s failure of producing diverse outputs. Memory bank with a size significantly larger than the batch size helps prevent this by storing various previously seen spots to increase the diversity during the reconstruction process.
The removal of histology data in Component I &III reduces STANDS’ performance in DDATD, as indicated by the lower accuracy and F1-score in ATD detection, and lower Macro-F1x NMI score in ATD subtyping (Supplementary Fig. 16a). We also notice an increase in false positives, particularly in normal domains that are histologically similar to surrounding normal tissues but exhibit high sparsity in ST data (as shown by the encircled area in the two rightmost panels in the top row of Supplementary Fig. 16c). We postulate that, when only using ST data, such normal domains tend to have a poor reconstruction due to their high sparsity, which distinguishes them from normal tissues in the absence of histological data.
Also shown in Supplementary Fig. 16a, omitting TF blocks in Component I &III also decreases STANDS’ performance in ATD detection and subtyping, respectively. This aligns with our expectation given that the TF block in Component I enhances ATD detection by facilitating complementary information exchange between data modalities, while the TF block in Component III integrates anomalous spot embeddings and reconstruction errors to inform anomaly clustering.
Finally, replacing the non-negative mapping matrix with a mutual-nearest neighbor (MNN) method38 in Component II worsens batch-mixing effect and domain type alignment, as indicated by the lower 1-ASW_batch and ASW_type scores in the middle panel of Supplementary Fig. 16a. This finding suggests that our approach, which is more oriented towards reconstruction-based task, is superior to MNN for multi-sample alignment in our context.
Discussion
Understanding the biological heterogeneity of pathogenic tissue domains across affected individuals serves as the cornerstone in the realm of personalized medicine. DDATD from multi-sample ST greatly facilitates such studies by providing critical insights into the molecular mechanisms and transcriptomic variations that drive the development of diseases. However, to the best of our knowledge, there is currently no computational methods that can utilize ST data for this purpose. In this study, we have introduced an innovative computational framework named STANDS to bridge this gap.
STANDS integrates and fulfills the three core tasks of DDATD: detecting, aligning, and subtyping ATDs across multiple ST samples. STANDS’ remarkable features include formulating the ATD detection problem under a generative model-based framework to significantly mitigate the batch variation interference, utilizing multimodal information from both histology images and spatial gene expression to enhance DDATD’s sensitivity and precision, transferring knowledge from scRNA-seq data when normal ST datasets are unavailable as references, utilizing “style-transferring” techniques to diminish nonbiological variations among ATDs across samples so that common and individual-specific ATDs can be discerned. These features effectively tackle the primary challenges in DDATD from multi-sample ST and collectively contribute to STANDS’ unparalleled performances in fulfilling the three tasks under various scenarios, as evidenced by our extensive benchmark studies using diverse real datasets from different platforms (10x Visium, Slide-seqV2), species (human, mouse) and tissues (breast, embryo, pancreas). Despite these advantages, there is still room for STANDS’ future improvement. For instance, the current GAN model can be replaced with an adapted denoising diffusion probabilistic model. This next-generation generative model could be more accurate in reconstructing normal observations, thereby further reducing the false positives in ATD detection.
In summary, the main contributions of this study include introducing STANDS as the first dedicated method for detecting ATDs from ST data. STANDS distinguishes itself from existing ST alignment methods (e.g., STAligner19) in preserving the original data scale and semantic integrity of aligned data, as well as being robust to unalignable non-overlapping domain types and ATDs. Additionally, STANDS is currently the only method that can further dissect ATDs into biologically distinct subdomains and discern them as either shared across samples or specific to individual samples. The study also introduces SGD and multi-SGD as the first metrics that incorporate spatial relationships among observations for a more effective evaluation of spatial clustering results. Moreover, STANDS are not restricted to anomaly detection in ST. It also can be used to detect, align, and classify anomalous single cells across scRNA-seq datasets, given its capability of treating target spatial spots as single-cells, e.g., when cross-referencing scRNA-seq data. Furthermore, the core concept of STANDS’ integrated framework for detecting and subtyping anomalies can potentially be applied to other omics data modalities, and its transfer-learning-based reconstruction strategy offers a promising means for utilizing more accessible data modalities to inform anomaly detection in emerging or rarer data modalities, such as scATAC-seq. Therefore, we anticipate STANDS will prove useful for the diagnosis of pathogenic tissue regions, the discovery of novel or individual-specific pathogenic sources, and the development of targeted therapies.
Methods
Anomalous tissue domain detection
As illustrated in the C1 part of Fig. 1b, module I consists of a generator and a discriminator. The generator itself is composed of four subcomponents: an encoder, a decoder, a transformer fusion (TF) block, and a memory bank. The encoder employs a GAT and a ResNet-GAT hybrid network to generate spot embeddings based on spatial gene expression data and the associated histology image, respectively:
were, \({x}_{i}^{g}\) denotes the gene expression vectors of spot \(i\), \({x}_{i}^{p}\) the segmented patches of the histology image, \(G=\left(V,E\right)\) the graph representation of all spatial spots, \({z}_{i}^{g}\) and \({z}_{i}^{p}{{\boldsymbol{\in }}}{{\mathbb{R}}}^{d}\) the transcriptomic and image patch embeddings for spot \(i\), respectively. These embeddings are then fused using a TF block:
The memory bank is essentially an embedding queue \({{\bf{Q}}}{{\boldsymbol{\in }}}{{\mathbb{R}}}^{{N}_{{mem}}{{\boldsymbol{\times }}}2d}\) filled with \(z\), where \({N}_{{mem}}\) denotes the number of in-memory embeddings. It provides an attention-based means to reconstruct \(z\) as \(\widetilde{z}{{\boldsymbol{\in }}}{{\mathbb{R}}}^{2d}\):
where \(\tau\) is a temperature hyperparameter. \({{\bf{Q}}}\) is continuously updated during training by enqueuing recent \(\widetilde{z}\) and dequeuing the oldest to maintain a balance between preserving previously learnt features and adapting to new spots, thereby mitigating the mode collapse risk. The decoder consists of a Multi-Layer Perceptron (MLP) network and a ResNet-based deconvolution network for reconstructing the gene expression vector \({\hat{x}}_{i}^{g}\) and image patch \({\hat{x}}_{i}^{p}\) from their respective \({\widetilde{z}}_{i}^{g}\) and \({\widetilde{z}}_{i}^{p}\).
The discriminator \(D\) comprises an encoder, similar to the generator’s encoder, and an MLP-based classifier. \(D\) is trained to distinguish between \(x=({x}^{g},\,{x}^{p})\) and \(\hat{x}=({\hat{x}}^{g},{\hat{x}}^{p})\). The total loss functions for the generator (\({{{\mathcal{L}}}}_{{Gen}}\)) and the discriminator (\({{{\mathcal{L}}}}_{D}\)) are defined as:
where \({{\rm{\xi }}}=\epsilon \hat{x}+\left(1-\epsilon \right)x,\,\epsilon \in \left({\mathrm{0,1}}\right)\). Here, \({{{\mathcal{L}}}}_{{rec}}\) denotes the data reconstruction loss, while \({{{\mathcal{L}}}}_{{adv}}\) the adversarial loss. \(\alpha,\beta,\) a\({nd}\) \(\lambda \ge 0\) represent the weights of each loss function, \({{\rm{\gamma }}}\in \left[{\mathrm{0,1}}\right]\) represents the relative importance between the gene expression and imagery data. \(D\left({\hat{x}}_{i}\right){{\boldsymbol{\in }}}{{\mathbb{R}}}^{h}\) is the discriminator’s output for \({\hat{x}}_{i}\), and \({\mathbb{E}}\left[ D\left({\hat{x}}_{i}\right)\right]\in \left[0,\,1\right]\) represents the probability that \({\hat{x}}_{i}\) is classified as real by \({D}\). Additionally, a gradient penalty term applied to \({{\rm{\xi }}}\) ensures the Lipschitz continuity of the discriminator and is critical for maintaining the stability of the adversarial training process39.
When only transcriptomic data (scRNA-seq or ST) is available for referencing, GAN module I undergoes specific modifications. Specifically, in the case of cross-referencing scRNA-seq, the GAT-based encoder of the generator is replaced by a two-layer MLP to generate \({x}_{i}^{g}\):
Similarly, the GAT-based encoder of the discriminator is replaced with the two-layer MLP. Moreover, without the image modality, the ResNet-based image encoder/decoder and the TF block are omitted so that \({z}_{i}={z}_{i}^{g}\) and the memory bank \({{\bf{Q}}}\) has a size of \({{\mathbb{R}}}^{{N}_{{mem}}{{\boldsymbol{\times }}}2d}\). All other components remain unchanged.
Upon completing the training, STANDS is utilized to reconstruct spots in the target datasets. The reconstruction fidelity for a given spot \(j\) is quantified using an anomalous score (\({{{\mathcal{d}}}}_{j}\)), computed as the cosine dissimilarity between \(D\left({\hat{x}}_{j}\right)\) and \(D\left({x}_{j}\right)\):
A higher value of \({{{\mathcal{d}}}}_{j}\) indicates a less accurate reconstruction, implying spot \(j\) is more likely to be an anomaly. As such, we model the anomaly scores’ distribution as a univariate Gaussian Mixture Model (GMM) with two components: one for anomalous spots (component 1) and the other for normal ones (component 2). We specify the prior for anomaly abundance as a beta distribution and the priors for the mean and variance of the two Gaussian components as a Normal Inverse Chi-squared (NIX) distribution. Utilizing the Maximum A Posteriori (MAP)-EM algorithm, we infer the parameters for both Gaussian components and then assign spots into either normal or anomalous groups based on their probabilities within each component. Specifically, let \(\Theta=\left\{\pi,{\mu }_{k},{\sigma }_{k}^{2},\forall k\in \left\{{\mathrm{1,2}}\right\}\right\}\) represent the GMM parameters, where \(\pi \in \left[{\mathrm{0,1}}\right]\) represents the proportion of anomalies, and \({\mu }_{k},{\sigma }_{k}^{2}\) represent the mean and variance for the \(k\)-th component, respectively, with the constraint that \({\mu }_{1} > {\mu }_{2}\). Then, the probability density function of \({{{\mathcal{d}}}}_{i}\) can be formulated as:
Parameters for the priors in the GMM are empirically set based on the reference dataset’s anomaly scores \({{{\rm{\delta }}}}_{i},\forall i\in \left[1,\, {N}_{{ref}}\right]\):
The values of \({{\rm{a}}}\) \({{\rm{and}}}\) \({{\rm{b}}}\) can be adjusted if prior knowledge about anomaly abundance is available. The complete data log likelihood for the posterior, denoted as \({{\ell}}_{{{\mathcal{c}}}}\left(\Theta \right)\), is expressed as:
where, \({{{\rm{z}}}}_{i}\) denotes the component membership of spot \(i\). In the \(t\)-th iteration of the E-step, the expected sufficient statistics \({\bar{{z}_{i}}}^{(t)}\) is derived from \({\Theta }^{(t-1)}\). In the subsequent M-step, \({\Theta }^{(t-1)}\) is updated to \({\Theta }^{(t)}\) by maximizing the auxiliary function \(Q\big(\Theta,{\Theta }^{(t-1)}\big)={\mathbb{E}}\big[{{\ell}}_{{{\mathcal{c}}}}\big(\Theta \big)\big({\Theta }^{(t-1)}\big)\big]\). Refer to Supplementary Note 1.4 for details about the model inference.
Multimodal learning of spatial gene expression data and histology image
To effectively integrate and harness spatial gene expression data and the associated histology images, STANDS generates spot embeddings from both data types, which are subsequently fused into multimodal embeddings for each spot using a TF block. A histology image is first segmented into patches centered around each spatial spot, adhering to the methodology outlined by Pang et al.40. The image patch for spot \(i\), represented as \({x}_{i}^{p}\in {{\mathbb{R}}}^{3\times W\times H}\), is processed through a pre-trained ResNet to yield initial embeddings \({\bar{x}}_{i}^{p}\in {{\mathbb{R}}}^{v}\), where \(\mbox{('')} 3\hbox{''}\) indicates the number of channels (RGB), and \(W\) and \(H\) denote the patch width and height, respectively. Meanwhile, we convert the locations of spatial spots into an undirected neighborhood graph \(G=\left(V,E\right)\) with a pre-defined neighbor number \(k\), where \(V\) and \(E\) represent the spot and edge sets, respectively. In our implementation, \(k\) is set to be 6. The adjacency matrix \({{\bf{A}}}\in {{\mathbb{R}}}^{{N}_{{spot}}\times {N}_{{spot}}}\) of \(G\) is defined as:
where \({N}_{k}\left(i\right)\) represents the set of proximity-based \(k\)-nearest neighbors of spot \(i\). Here, \(\widetilde{{{\bf{A}}}}\) extends \({{\bf{A}}}\) by adding self-loops and is utilized by the GATv241, a two-layer graph attention auto-encoder, in the generation of transcriptomic and image embeddings. For instance, we calculate an attention score \({{{\rm{\alpha }}}}_{i,j}^{\left(l\right)}\) between a given spot \(i\) and its neighbor \(j\) on the \(l\)-th encoder layer using the formula:
where, \({z}_{i}^{\left(l\right)}\in {{\mathbb{R}}}^{d}\) is spot \(i\)’s embedding generated by the \(l\)-th encoder layer. The matrix \({{{\bf{Z}}}}^{\left(l\right)}\in {{\mathbb{R}}}^{{N}_{{spot}}\times d}\), which compiles all \({z}_{i}^{\left(l\right)},\forall i\in \left[1,{N}_{{spot}}\right]\), is formulated as:
where, \({{{\bf{W}}}}_{a}^{\left(l\right)}\) stores all \({{{\rm{\alpha }}}}_{i,j}^{\left(l\right)}\), and \({{\rm{\sigma }}}\) denotes a nonlinear activation function. Note that spot \(i\)’s initial embedding for the \(0\)-th layer, \({z}_{i}^{\left(0\right)}\), depends on the data type: \({x}_{i}^{g}\) for transcriptomic data and \({\bar{x}}_{i}^{p}\) for histology image. The transcriptomic and image embeddings outputted by the GATv2 encoder, denoted as \({{{\bf{Z}}}}^{g}\in {{\mathbb{R}}}^{{N}_{{spot}}\times d}\) and \({{{\bf{Z}}}}^{p}\in {{\mathbb{R}}}^{{N}_{{spot}}\times d}\) respectively, are concatenated into \({{{\bf{Z}}}}^{{concat}}\in {{\mathbb{R}}}^{{N}_{{spot}}\times 2d}\). This concatenated matrix serves as the input to a multi-head transformer block for data fusion. To elaborate, let \(m\) denote the number of attention heads such that \(2d\) is divisible by \(m\). \({{{\bf{Z}}}}^{{concat}}\) is split into \(m\) sub-embeddings \({{{\bf{Z}}}}_{1},\cdots,{{{\bf{Z}}}}_{m}\in {{\mathbb{R}}}^{{N}_{{spot}}\times 2d/m}\) followed by their mappings to the corresponding query, key and value matrices (\({{{\bf{Q}}}}_{t},{{{\bf{K}}}}_{t},{{{\bf{V}}}}_{t}{{\boldsymbol{\in }}}{{\mathbb{R}}}^{{N}_{{spot}}\times d}\)) as:
where, \({{{\bf{W}}}}_{t}^{Q},\,{{{\bf{W}}}}_{t}^{K},\,{{{\bf{W}}}}_{t}^{V}\in {{\mathbb{R}}}^{\left(2d/m\right)\times d}\) are trainable weight matrices. The output embeddings \({{{\bf{H}}}}_{t}\in {{\mathbb{R}}}^{{N}_{{spot}}\times d}\) from attention head \(t\) are calculated as:
which essentially is an enhanced representation of a subspace of \({{{\bf{Z}}}}^{{concat}}\). Finally, the output embeddings from all attention heads are fused into the final spot embeddings \({{\bf{Z}}}\in {{\mathbb{R}}}^{{N}_{{spot}}\times 2d}\) as:
where, \({{{\bf{W}}}}^{o}{{\boldsymbol{\in }}}{{\mathbb{R}}}^{{md}\times 2d}\) represents the trainable weight matrix for fusing \({{{\bf{H}}}}_{t},\forall t\in \left[1,\, m\right]\).
Multi-sample ST data alignment
As illustrated in the C2 part of Fig. 1b, this task proceeds in two steps: Initially, each normal spot in target datasets is paired with its most similar spot in the reference dataset, forming a “kin” pair indicative of shared biological contents. Subsequently, based on these “kin” pairs, STANDS learns a “style-divergence” matrix which encodes the batch divergences between the target and reference datasets in its rows. This matrix allows the mapping of target datasets to the reference data space in a “style-transfer” manner.
In the first step, the generator of module II learns to reconstruct the embeddings of target spots using those of reference spots, while the discriminator learns to distinguish between the authentic and generated spots. Specifically, let \({{{\bf{Z}}}}_{T}\in {{\mathbb{R}}}^{{N}_{T}\times d},{{{\bf{Z}}}}_{R}\in {{\mathbb{R}}}^{{N}_{R}\times d}\) denote the transcriptomic embeddings of target and reference spots, respectively. \({N}_{T}\) and \({N}_{R}\) denote the number of target and reference spots, respectively. \({{\bf{M}}}\in {{\mathbb{R}}}^{{N}_{T}\times {N}_{R}}\) denotes a trainable non-negative mapping matrix. The generator reconstructs \({\hat{{{\bf{Z}}}}}_{T}\) as:
where ReLU function imposes a non-negative constraint on \({{\bf{M}}}\). \(\bar{{{\bf{A}}}}{{\boldsymbol{\in }}}{{\mathbb{R}}}^{{N}_{T}\times {N}_{R}}\) is a kNN adjacency matrix that integrates spatial neighborhood information into the calculation. \({N}_{k}\left(i\right)\) represents the set of spot \(i\)’s k-nearest neighboring reference spots. The loss functions of the generator and discriminator in module II are given by:
where \(\widetilde{{{\bf{Z}}}}= \epsilon \hat{{{\bf{Z}}}}+\left(1-\epsilon \right){{\bf{Z}}},\epsilon \in \left({\mathrm{0,1}}\right)\), and \(\alpha,\beta,\lambda \ge 0\) represent the weights of the loss terms. After training, the column index of the maximum value in the \(i\)-th row of \({{\bf{M}}}\) points to the reference spot that is “kin” to the \(i\)-th target spot.
The two spots of a “kin” pair are presumed to share similar biological contents so that the reference spot can be approximated by removing the “style-divergence” (batch variations) from the target spot. Therefore, in the second step, a “style”-transfer GAN (module III) is employed to learn the “style-divergences” between target and reference datasets as a matrix \({{\bf{S}}}\in {{\mathbb{R}}}^{{N}_{{batch}}\times d}\). Specifically, for each target spot \(i\), the encoder within the generator of module III maps the gene expression vector \({x}_{i}\) to a latent embedding \({z}_{i}\in {{\mathbb{R}}}^{d}\). This encoder and the one within module I share the same network architectures but are trained independently, with the former initialized using the latter’s trained weights. Here, \({z}_{i}\) approximates the embedding of its “kin” reference spot \(j\) as follows:
where \({b}_{i}\in {{\mathbb{R}}}^{{N}_{{batch}}}\) denotes spot \(i\)’s one-hot batch identity vector, and \({G}_{i}\) is the graph representation of the dataset containing spot \(i\). The generator’s decoder then reconstructs \({\hat{x}}_{i}^{g}\) from \({\hat{z}}_{i}\), while the discriminator of module III learns to distinguish between \({x}_{i}^{g}\) and \({\hat{x}}_{i}^{g}\). The loss functions for the generator and discriminator are:
where \(\alpha,\beta,\lambda\) and \({\widetilde{x}}_{R}\) mirror their counterparts in module II. By passing through the trained generator of module III, spots across multiple target datasets are allowed to be collectively aligned in the common reference data space.
Subtyping anomalous tissue domains across multiple datasets
Initially, identified anomalous spots across multiple target datasets are aligned by module III in the common reference space, effectively reducing the confounding batch variations in anomaly subtyping. Then, as illustrated in the C3 part of Fig. 1b, the embedding and reconstruction residual of each aligned anomalous spot are fused into a comprehensive embedding that is informative on anomaly subtypes. Specifically, for a given anomalous spot \(i\), let \({x}_{i}^{g}\) and \({x}_{i}^{p}\) denote its aligned gene expression and image patch vectors, respectively; \({\hat{x}}_{i}^{g}\) and \({\hat{x}}_{i}^{p}\) denote the reconstructed vectors from \({x}_{i}^{g}\) and \({x}_{i}^{p}\), respectively; \({r}_{i}^{g}\) and \({r}_{i}^{p}\) denote the reconstruction residuals of gene expression and image patch vectors, respectively; \({z}_{i}\) and \({{{\rm{\zeta }}}}_{i}\) represent the module I-generated embeddings of \({x}_{i}\) and \({r}_{i}\), respectively. Then, we have:
where, \({z}_{i}^{*}\) represents the fused embedding of anomaly \(i\). DEC42, a discriminatively boosted clustering algorithm, groups anomalies into clusters based on their \({z}^{*}\). It applies a Cauchy kernel to \({z}_{i}^{{\prime} }\) to calculate the soft assignment score (\({q}_{i,j}\)) of anomaly \(i\) to a cluster \(j\) as:
where, \({\mu }_{j}\) denotes the centroid of cluster \(j\), \(v\) the degree of freedom of the Cauchy kernel. The clustering loss function \({{\mathcal{L}}}\) is based on the KL-divergence between \(q\) and an auxiliary target distribution \(p\), defined as:
Essentially, anomalies with high-confident assignment are overweighed in the distribution \(p\). In practice, the iterative updating of \({{{\bf{W}}}}_{{tf}}\) and \(\mu\), aiming to minimize \({{\mathcal{L}}}\), nudges \(q\) toward \(p\) and incrementally transforms harder-to-cluster embeddings \({z}^{*}\) into easier ones. This self-paced clustering continues until the changes in anomalies’ hard assignments fall below a threshold or a predetermined number of iterations is reached. The resultant hard cluster assignments of anomalous spots correspond to their subtype labels. The number of clusters is assumed to be known or automatically inferred as described in Supplementary Note 1.5.
Model architecture and training
Anomalous tissue domain detection
Here, GAN module I is first trained on the reference dataset and then applied to the target data, generating reconstruction errors as anomaly scores for each target spot. GAN module I comprises a generator and a discriminator. During the training of GAN module I, we set a mini batch size of 128 and utilize the Adam optimizer with a learning rate of 3e-4.
The generator is further divided into an encoder, a memory bank, and a decoder. When using an ST dataset as reference, the encoder is a two-layer GAT of an architecture of 3000-512-256, with four 128-dimensional attention heads in the first layer and a single 256-dimensional attention head in the second layer. When histology data is available (e.g., for 10x Visium datasets), a pretrained ResNet-3443 is used to extract 256-dimensional visual features from 112 × 112 pixel image patches that are segmented from the histology image and centered around each spatial spot. These visual features are further encoded by another two-layer GAT, with the same architecture as used for encoding ST data, to capture the spatial relationships among neighboring patches. The 256-dimensional image and gene expression embeddings are then fused using a TF block comprising three transformer encoder layers, each with four 128-dimensional attention heads, to output 512-dimensional fused embeddings. Note that the encoder branch for visual features and the TF block is omitted in the absence of histology image. When cross-referencing an scRNA-seq dataset, a two-layer MLP network with an architecture of 3000-512-256 replaces the GAT in the encoder to generate gene expression embeddings at each spot. The batch (128) of embeddings output from the encoder is subsequently enqueued into the memory bank, which has a size of 512×512 for multimodal embeddings and 512 × 256 for single-modal embeddings, while an equal number of the oldest embeddings in the bank are dequeued. After memory bank-mediated embedding reconstruction, 256-dimensional single-modal gene expression embeddings are input to the decoder, while 512-dimensional multimodal embeddings are split into 256-dimensional image and gene expression embeddings before being fed into their respective decoders. The decoder for ST data is a two-layer MLP with an architecture of 256-512-3000, and the decoder for image data is a ResNet-34 decoder symmetric to the ResNet encoder, comprising transposed convolutional layers.
The discriminator, comprising an encoder and a four-layer MLP-based classifier, accepts pairs of original and reconstructed data. The architecture of its encoder mirrors that of the generator’s encoder, and the classifier has an architecture of 512-256(x3)−16 in the presence of image data or 256(x4)−16 otherwise. The discriminator is trained to maximize the L1-norm difference between the 16-dimensional output embeddings of the original and reconstructed data.
Multi-sample ST data alignment
Initially, plausible anomalous spots identified by GAN-module I are excluded from the target datasets to minimize their confounding effects during alignment. GAN module II’s generator processes gene expression embeddings of both reference and target spots generated by GAN module I’s encoder, training a non-negative mapping matrix to reconstruct the target embeddings from the reference embeddings. The discriminator is a four-layer MLP with an architecture of 512-256(x3)−16, aimed at maximizing the L1-norm difference between the original and reconstructed target embeddings. Once trained, the non-negative mapping matrix is utilized to identify kin pairs of reference and target spots, whose raw data are then input into GAN module III.
The encoders and decoders of the generator within GAN module III and module I share the same architectures but are trained independently, with the former initialized with the latter’s trained weights. GAN module III trains a matrix \(S \sim {n}_{b}\times 256\) that encompasses \({n}_{b}\) style embeddings representing various batch effects. These style embeddings are subtracted from their corresponding target spots’ embeddings to map the target spots to the common embedded reference space so as to transfer target datasets’ styles to the reference dataset’s. For each target spot, the generator’s decoder use its “style-transferred” embedding to reconstruct its kin reference spot, which is then paired with the original data as inputs to the discriminator whose architecture mirrors that of the discriminator in GAN module I. Lastly, the training of this module adopts a batch size of 128 and the Adam optimizer with a learning rate 3e-4.
Anomaly subtyping
Anomalous spots identified by the GAN module I are aligned in the reference data space using the trained GAN module III. Then, the frozen encoder and decoder from GAN module I are used to generate post-alignment embeddings of identified anomalous spots and their reconstruction errors, respectively. Using a specific encoder that mirrors the encoder of GAN module I’s generator but is trained independently, reconstruction errors are further converted into embeddings with same dimensions as the spot embeddings. The spot and reconstruction error embeddings are fused into 128-dimensional embeddings using a trainable TF block, consisting of three transformer layers, each with multiple 128-dimensional attention heads. Specifically, there are eight attention heads in a transformer layer when using multimodal data or four heads otherwise. The outputs are subsequently subjected to self-paced discriminatively boosted clustering. The training process iterates between clustering and fused embedding generation until the changes in anomalies hard assignments fall below a threshold (0.001) or a number of iterations (2e4) is reached.
Data preprocessing
In this study, we follow the standard pipeline of data preprocessing provided by the Scanpy44, SpatialDE45 and GeneClust46 packages. Specifically, mitochondrial and External RNA Controls Consortium (ERCC) spike-in genes are removed. Genes detected in fewer than 10 spots are excluded. We do not perform filtering on spatial spots to maintain spatial data integrity. Gene expression counts matrix are normalized by library size and then log-transformed. Finally, we select the top 3000 spatially variable genes (SVG) selected using SpatialDE as inputs to the STANDS.
Evaluation metrics
Anomalous tissue domain detection
Spatial grouping discrepancy (SGD)
We propose the SGD, a novel metric to assess both the accuracy of labels and the consistency of spatial structures. Specifically, spatial locations are represented as nodes in an undirected graph. Normal spots are isolated, while anomalous spots are connected to their k-nearest anomalous neighbors. Note that in the anomaly detection results, incorrectly identified spots as anomalies (false positives) become connected, and false negatives become isolated, which leads to a deviation from the local structures of the ground truth graph. Spots are divided into two regions: one includes true positives plus false positives (TP + FP) anomalies, and the other includes true positives plus false negatives (TP + FN) anomalies. We perform a bootstrap sampling of \(m\) sets of spots from these two regions, generating a collection \(S=\left\{{s}_{i}:\left\{{s}_{i}^{\left(1\right)},{s}_{i}^{\left(2\right)}\right\},\forall i\in \left[1,m\right]\right\}\). Subsequently, both cluster coefficients and degrees for spots within \({s}_{i}\) are calculated as follows:
for all \(i\in \left[1,m\right]\), every spot \(j\) in \({s}_{i}^{\left(r\right)},\) region \(r\in \left\{1:{TP}+{FP},2:{TP}+{FN}\right\}\), and label type \(l\in \left\{1:{{\rm{ground}}}{{\rm{truth}}},2:{{\rm{anomaly}}}{{\rm{detection}}}{{\rm{outcomes}}}\right\}\). Here, \(c{c}_{i,j}^{\left(r,l\right)}\) and \({d}_{j}^{\left(r,l\right)}\) represent the cluster coefficient and degree of spot \(j\) within region \(r\) from bootstrap sample \(i\), based on either the ground truth (\(l=1\)) or anomaly detection outcomes (\(l=2\)). \({k}_{j}\) denotes the number of neighbors connected to spot \(j\), \({E}_{j}\) the number of edges among these neighbors, \({e}_{j,n}\) the edge between spots \(j\) and \(n\), \({N}_{k}\left(j\right)\) the set of k-nearest neighbors of spot \(j\). We adopt both degree and cluster coefficient metrics because they reflect the centrality and neighborhood connectivity of spots, respectively.
Next, for any two bootstrap samples \(i\) and \(j\), we quantify the discrepancy in the distribution of their cluster coefficients or degrees using the Wasserstein distance, \(W({p}_{i,t},{p}_{j,t})\), defined as:
for every \(t\in \left\{1:{{\rm{degree}}},\, 2:{{\rm{cluster\; coefficient}}}\right\},\) and \(r\in \left[1:{TP}+{FP},2:{TP}+{FN}\right]\). Here, \({p}_{i,t}^{\left(r\right)}\) denotes the distribution of \(t\) for region \(r\) in the \(i\)-th bootstrap sample, and \(\Pi \left(p,q\right)\) represents the set of all joint distributions with marginals \(p\) \({and}\) \(q\), respectively. \(\gamma\) denotes a valid transport plan between these distributions. To capture high-order moments of distributional discrepancy, we apply a Gaussian-like kernel to the Wasserstein distance:
where \(\tau\) is a positive temperature hyperparameter. The Moore-Aronszajin theorem guarantees that this symmetric and positive-definite kernel induces a unique Reproducing Kernel Hilbert Space (RKHS)47. Finally, we define SGD metrics as Maximum Mean Discrepancy (MMD) scores for the metric in this RKHS:
where \({p}_{{true},t}\) and \({p}_{{detect},t}\) represent the sets of distributions for metric \(t\) (degree or cluster coefficient) derived from bootstrap samples in the contexts of ground truth and anomaly detection outcomes, respectively. Based on SGD, we further propose multi-SGD to measure the spatial discrepancy between spatial clustering results and ground truth that involves multiple domain types (see “Multi-type spatial grouping discrepancy” section below).
Multi-sample ST data alignment
The performance of multi-sample alignment is assessed using multiple metrics calculated on reduced t-SNE embeddings of aligned datasets. These metrics include integration local inverse Simpson’s index (iLISI)33, BatchKL25, and ASW_batch48 for evaluating batch mixing effects, and ASW_type48 for evaluating cross-batch domain (or spot) type alignment. Additionally, ARI is used to evaluate spatial clustering performed on aligned datasets.
iLISI. This metric measures the effective number of batches present in the local neighborhoods of spots across aligned datasets by calculating a score that represents the degree of local batch mixing. The score value ranges from 1 to \({N}_{{batch}}\), with a higher value indicating more effective batch mixing. To elaborate, a neighboring spot probability matrix is calculated as:
where \(i,j\in [1,{N}_{{spot}}]\), and \({x}_{i}\) denotes the reduced t-SNE embeddings of spot \(i\), \({N}_{k}\left(i\right)\) the set of proximity-based \(k\)-nearest neighbors of spot \(i\), and \({p}_{i,j}\) the probability that spot \(i\) is aligned to spot \(j\). Then, the iLISI score is calculated as:
where, \({{\bf{B}}}={\left({b}_{1},\, {b}_{2},\cdots,\, {b}_{n}\right)}^{T}\in {{\mathbb{R}}}^{{N}_{{spot}}\times {N}_{{batch}}}\) represents a batch-identity matrix and \({b}_{i}\) represent the one-hot batch-identity vector of spot \(i\).
BatchKL. This metric assesses the effectiveness of batch correction by calculating mixing Kullback-Leibler (KL) divergences. It reflects the batch diversity across aligned datasets, with a lower value indicating more effective batch mixing. Initially, 100 spots are randomly sampled from all batches, followed by the calculation of the regional mixing KL divergence as:
where, \({q}_{b}\) represents the proportion of spots from batch \(b\) in the entire sample, while \({p}_{b}\) represents the average proportion of spots from batch \(b\) within the \(k\)-nearest neighborhood of each sampled spot in the reduced t-SNE space.
ASW_batch &ASW_type. The two metrics represent the average silhouette width of aligned spots based on their batch identities (ASW_batch) and domain types (ASW_type). A higher silhouette coefficient implies that observations within identical groups form compact clusters, while those belonging to different groups are well-separated. Therefore, a lower ASW_batch score indicates more effective batch mixing, while a higher ASW_type score indicates more accurate cross-batch domain (or spot) type alignment.
Adjusted Rand Index (ARI). This metric assesses the spatial clustering results, with a higher value indicating more consistent clustering with the ground truth. Let \(n\) represents the total number of spots, \({n}_{{ij}}\) the number of spots of type \(i\) within cluster \(j\), \({a}_{i}\) the total number of spots of type \(i\), \({b}_{j}\) the total number of spots within cluster \(j\). Then ARI is calculated as:
Anomaly subtyping
Multi-type spatial grouping discrepancy (multi-SGD)
This metric assesses the consistency between the anomaly subtyping outcomes and the ground truth subdomain labels, taking into account the spatial relationships among spots. For \(\kappa > 2\) subtypes, we adopt the One-vs-Rest methodology to calculate an SGD score for each subtype, as detailed in the “Anomalous tissue domain detection” section. This involves mapping annotations generated by the subtyping method to the ground truth annotations using the COIN-OR Branch and Coin solver49 to solve the following mixed-integer programming problem:
where \(t\in \left\{{{\rm{degree}}},{{\rm{cluster\; coefficient}}}\right\}.\) Here, \({y}_{i,j}=1\) indicates that the \(i\)-th anomalous subtype is mapped to the \(j\)-th subtyping annotation. \({N}_{i}\) denotes the number of spots belonging to subtype \(i\), \({N}_{{total}}\) the total number of anomalous spots. \({{\rm{SGD}}}\big({p}_{i,{true},t}{||}{p}_{j,{sub},t}\big)\) represents the subtype-specific SGD score for the \(i\)-th true subtype when mapped to the \(j\)-th generated annotation (refer to equation 1). Finally, the multi-SGD for metric \(t\) is determined as:
Normalized Mutual Information (NMI). This nonnegative metric evaluates the consistency between clustering results with the ground truth, with a higher value indicating a more accurate clustering. NMI is defined as:
where, \({n}_{{ij}}\) represents the number of true positives of anomaly type \(i\) within cluster \(j\), \({a}_{i}\) the total number of true positives of anomalous type \(i\), \({b}_{j}\) the total number of true positives within cluster \(j\).
Benchmark methods
Benchmark overview
Anomalous tissue domain detection
For benchmarks of the ATD detection subtask, we select five supervised methods, including Spatial-ID, scPred, CHETAH, scmap, and CAMLU, as well as two unsupervised methods, including SCEVAN and CopyCAT. All methods, except Spatial-ID, are originally designed for detecting anomalous single cells in scRNA-seq data. Each supervised methods trains a classifier on an annotated reference scRNA-seq dataset, which is then applied to classify target spots into known types. Specifically, Spatial-ID employs a deep neural network (DNN) pretrained on the reference scRNA-seq dataset. During inference, it utilizes a variational graph autoencoder (VGAE) to yield spot embeddings, which are then fed into the DNN classifier to generate spot pseudo-labels. Meanwhile, it trains another self-supervised DNN classifier to predict spot types against their pseudo-labels, identifying spots with a maximum type assignment probability below a threshold as anomalies. scPred trains a support vector machine (SVM) classifier on the annotated reference using the most informative principal features selected via a Wilcoxon signed-rank test. This classifier is used to classify target cells into known types and identify those with maximum assignment probability below a threshold as anomalies. CHETAH builds a hierarchical classification tree from reference data, computing cell-type specific gene expression profiles at each tree node. During inference, target cells are classified by traversing the tree, with the traversal path determined based on their correlations (i.e., confidence scores) with gene expression profiles at intermediate tree nodes. Target cells with a confidence score below a threshold at the root node are deemed anomalous. scmap calculates gene expression profile similarities between target cells to cell type centroids in the reference dataset, assigning them to the type with highest similarity. Target cells with the highest similarity score below a threshold are identified as anomalous. The aforementioned supervised methods identify target cells with low assignment confidence as anomalies, which however increases the false positive risks due to confusing normal cells with uncertain assignment with genuine anomalies. Conversely, CAMLU is a reconstruction-based method that sidesteps the requirement for annotated reference. It trains an autoencoder to reconstruct genes in the reference dataset which is then applied to the target dataset, selecting genes that demonstrate the largest discrepancies between reconstruction errors of the reference and target datasets as discriminative features. These genes are utilized in a hierarchical clustering to categorize target cells as normal or anomalous.
Unlike the supervised benchmarks, the two unsupervised benchmarks, SCEVAN and CopyCAT, are directly applied to the target ST datasets. They both initially identify a set of highly confident normal cells to serve as a gene copy number baseline. Next, the gene copy number profiles of target cells are estimated from the baseline using a joint segmentation algorithm in SCEVAN and a Poisson-Gamma model in CopyCAT. Utilizing these profiles, both methods performs hierarchical clustering to group cells into clusters, identifying those significantly enriched in predefined normal cells as normal and others as anomalous.
Multi-sample ST data alignment
Benchmarks for the ATD alignment subtask include two well-established batch correction methods for scRNA-seq, ComBat and Harmony, alongside two recent methods for ST, GraphST and STAligner. ComBat utilizes a Bayesian framework with empirical priors to estimate and correct for both additive and multiplicative batch effects across samples. Harmony clusters cells in a low-dimensional embedded space, maximizing intra-cluster batch diversity, and then applies linear batch correction using the cluster centroids. GraphST is designed for aligning spatially adjacent ST datasets as it relies on PASTE50 to align histological images of adjacent datasets to acquire consensus spatial coordinates. It corrects batch effects by constructing a shared neighborhood graph that connects spatially adjacent spots across samples, reducing cross-sample batch variations through node feature smoothing in a self-supervised contrastive graph learning. STAligner integrates multiple ST datasets, whether spatially adjacent or not, into a single graph to yield spot embeddings using GAT, based on which positive and negative spot pairs are identified. Then batch variations are corrected by iteratively optimizing between spot embeddings and a contrastive learning triplet loss computed on the positive and negative pairs.
Anomaly subtyping
Three celebrated spatial clustering methods, including GraphST, STAGATE, and iStar, are chosen to benchmark ATD subtyping. GraphST models spatial gene expression using a graph, which is further augmented with a locally corrupted graph. Next, it employs a GCN to conduct a self-supervised contrastive learning between the two graphs, yielding spatial spot embeddings for spatial clustering. iStar utilizes a hierarchical vision transformer (HViT) pretrained on public histology images to yield both local and global image features for predicting super-resolution gene expressions using a weakly supervised feed-forward neural network (FFN). A k-means clustering is then performed using gene embeddings encoded by the penultimate layer of the FFN to cluster spots into different subtypes. STAGATE also models spatial gene expression using a graph and generates low-dimensional spot embeddings using a reconstruction-based GAT, which serve as input to an off-the-shelf clustering algorithm for subtyping.
Benchmark implementations
Anomalous tissue domain detection
This series of experiments spans three scenarios: detecting ATDs from a single target dataset, from multiple target datasets, and cross-referencing scRNA-seq data. In the first (Exp ID = 1 and 4), second (Exp ID = 3, 5, 6, 7, and 8) and third (Exp ID = 2) scenarios, five supervised methods, including Spatial-ID, scPred, CHETAH, scmap, and CAMLU, are trained on the reference ST dataset, treating spatial spots as single-cells and domain types as cell types. These methods are then applied to the target datasets— scPred, CHETAH, scmap, and Spatial-ID compute an assignment confidence score to each target spot, labeling those below an implicitly specified threshold as anomalous. CAMLU, on the other hand, reconstructs the target datasets, selecting the top 500 feature genes exhibiting significant discrepancies in reconstruction errors compared to the reference dataset. Using these feature genes, target spots are clustered into normal and anomalous groups via a hierarchical clustering. During inference, all methods except Spatial-ID treat target spots as single-cells. Spatial-ID accounts for spatial relationships among target spots by incorporating their adjacency matrix during spot embedding generation. Additionally, in the third scenario, two unsupervised methods, i.e., SCEVAN and CopyCAT, are directly applied to target ST datasets, treating target spots as single-cells. Both methods perform hierarchical clustering to group spots into clusters based on their estimated gene copy number profiles. Clusters highly enriched in predefined highly confident normal spots in the enrichment analysis (P-value \(\le\) 0.05) are identified as normal and others as anomalous. In all experiments, benchmark methods adopt the default hyperparameter values, such as anomaly score thresholds, clustering algorithm parameters, and significance levels for statistical tests.
Multi-sample ST data alignment
Experiments for this task involve three ST datasets, either vertical or non-adjacent. The benchmarks include two methods for aligning scRNA-seq, ComBat and Harmony, and two for aligning ST datasets, GraphST and STAligner. ComBat and Harmony are directly applied to the ST datasets, treating spatial spots as single-cells and disregarding their spatial relationships. In experiments involving vertical datasets, GraphST first utilizes PASTE to obtain consensus spatial coordinates, with which spatial spots across datasets are positioned in a common tissue space for alignment. In experiments involving nonadjacent datasets (Exp ID = 9, 10, 12, and 14), whose spatial coordinates are unalignable, GraphST utilizes consensus original spatial coordinates in the alignment process as a compromise. Conversely, STAligner can handle both vertical and nonadjacent ST datasets through contrastive learning with positive and negative pairs of anchor spots. All benchmarks are evaluated with parameter settings recommended by the original studies.
Anomaly subtyping
Given the performance of ATD subtyping heavily depends on the quality of detected and aligned anomalous spots, we use composite methods comprising of methods specifically designed for each individual task as benchmarks. Experiments for this subtask involves either single or multiple target datasets.
In the first scenario (Exp ID = 18-21), six composite benchmarks are constructed, including CAMLU-GraphST, scPred-GraphST, CHETAH-GraphST, scmap-GraphST, SpatialID-iStar, and SpatialID-STAGATE. The first method in each composite name identifies ATDs, while the second clusters them into subtypes. Since this scenario only involves single target dataset, data alignment method is unnecessary. The subtyping methods vary in implementations: GraphST and STAGATE convert target spots into embeddings and employ their built-in clustering algorithms to group the embedded anomalous spots identified by the first method into subtypes. iStar is excluded in experiments (Exp ID = 17 and 20) involving Slide-seqV2 and Stereo-seq datasets, both of which are devoid of histology images. In other experiments, image patches covering the identified anomalous spots are segmented and converted into visual features using a pretrained visual feature extractor. iStar is trained to predict the gene expression profile at each target spot using a DNN, with the penultimate layer’s outputs serving as input spots’ embeddings. iStar’s k-means clustering algorithm then utilizes embeddings of anomalous spots to group them into subtypes.
The second scenario (Exp ID = 15-17 and 22-24) involves multiple target datasets, which necessitates data alignment methods. To meet this requirement, GraphST is added to the CAMLU-GraphST, scPred-GraphST, CHETAH-GraphST, and scmap-GraphST; ComBat to the SpatialID-iStar; and STAligner to the SpatialID-STAGATE. GraphST and STAligner align target datasets, generating post-alignment spot embeddings. The built-in clustering algorithms of GraphST and STAGATE use post-alignment embeddings of identified anomalous spots to cluster them into subtype groups. Since iStar trains the gene expression predictor using original gene expression data, ComBat, which preserves the original data scale post-alignment, is combined with SpatialID-iStar. This composite method are only used in experiments wherein datasets are associated with histology data (Exp ID = 15,16, 22, and 24). Specifically, Spatial-ID identifies anomalous target spots, iStar extracts visual features from the histology image associated with each target dataset, and ComBat aligns target datasets. Subsequently, iStar is trained on the target spots to predict their post-alignment gene expressions using the extracted visual features, in the meanwhile generating spot embeddings from the penultimate layer of the predictor. Finally, iStar’s built-in clustering algorithm cluster identified anomalous spots into subtypes using their spot embeddings. All component methods in the benchmarks adopt their default hyperparameter settings, and the true number of clusters is assumed to be known.
Reporting summary
Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.
Data availability
All experimental datasets involved in this paper are available from their respective original sources: The 10x-Visium datasets of healthy human breast tissues (10x-hNB datasets) are available at GSE195665; The 10x-Visium datasets of human breast cancer tissues (10x-hBC datasets) are available at GitHub [https://github.com/almaan/her2st/tree/master]; The 10x-Visium datasets of human primary sclerosing cholangitis tissue (10x-hPSC datasets) and human liver caudate lobe tissue are available at GSE243977; The 10x-Visium datasets of human renal cell cancer tissue (10x-hRCC datasets) are available at GSE175540; The scRNA-seq dataset of human pancreatic ductal (sc-hPD) and 10x-Visium datasets of the human pancreatic ductal adenocarcinomas (10x-hPDAC) are available at GSE111672; The slide-seqV2 datasets of mouse embryo tissues (ssq-mEmb datasets) are available at GSE197353; The Stereo-seq datasets of mouse embryo tissue (Stereo-mEmb datasets) are available at CNP0001543. Source data are provided in this paper. Source data are provided with this paper.
Code availability
An open-source Python implementation of the STANDS package along with the documentation and tutorial for running it are available at GitHub [https://github.com/Catchxu/STANDS]. We have obtained a DOI for our Github repository by linking it to Zenodo51. The Zenodo DOI is: https://doi.org/10.5281/zenodo.13375297.
References
Maus, R. L. et al. Resolving the heterogeneous tumor-centric cellular neighborhood through multiplexed, spatial paracrine interactions in the setting of immune checkpoint blockade. Cancer Res. Commun. 2, 78–89 (2022).
Arora, R. et al. Spatial transcriptomics reveals distinct and conserved tumor core and edge architectures that predict survival and targeted therapy response. Nat. Commun. 14, 5029 (2023).
Shinagare, A. B., Krajewski, K. M., Braschi-Amirfarzan, M. & Ramaiya, N. H. Advanced renal cell carcinoma: role of the radiologist in the era of precision medicine. Radiology 284, 333–351 (2017).
Yang, J., Chen, H., Yan, J., Chen, X. & Yao, J. in International Conference on Learning Representations (2021).
Stepec, D. & Skocaj, D. in Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition 3785-3792 (2021).
Hu, J. et al. SpaGCN: Integrating gene expression, spatial location and histology to identify spatial domains and spatially variable genes by graph convolutional network. Nat. Methods 18, 1342–1351 (2021).
Dries, R. et al. Giotto: a toolbox for integrative analysis and visualization of spatial expression data. Genome Biol. 22, 78 (2021).
Zhao, E. et al. Spatial transcriptomics at subspot resolution with BayesSpace. Nat. Biotechnol. 39, 1375–1384 (2021).
Zhang, D. et al. Inferring super-resolution tissue architecture by integrating spatial transcriptomics with histology. Nat Biotechnol (2024).
Dong, K. & Zhang, S. Deciphering spatial domains from spatially resolved transcriptomics with an adaptive graph attention auto-encoder. Nat. Commun. 13, 1739 (2022).
Long, Y. et al. Spatially informed clustering, integration, and deconvolution of spatial transcriptomics with GraphST. Nat. Commun. 14, 1155 (2023).
Hu, J. et al. Deciphering tumor ecosystems at super resolution from spatial transcriptomics with TESLA. Cell Syst. 14, 404–417. e404 (2023).
Kleshchevnikov, V. et al. Cell2location maps fine-grained cell types in spatial transcriptomics. Nat. Biotechnol. 40, 661–671 (2022).
Shen, R. et al. Spatial-ID: a cell typing method for spatially resolved transcriptomics via transfer learning and spatial embedding. Nat. Commun. 13, 7640 (2022).
Li, Z., Wang, Y., Ganan-Gomez, I., Colla, S. & Do, K. A. A machine learning-based method for automatically identifying novel cells in annotating single-cell RNA-seq data. Bioinformatics 38, 4885–4892 (2022).
Sprang, M., Andrade-Navarro, M. A. & Fontaine, J.-F. Batch effect detection and correction in RNA-seq data using machine-learning-based automated assessment of quality. BMC Bioinforma. 23, 1–15 (2022).
Xu, K. et al. Domain adaptive and fine-grained anomaly detection for single-cell sequencing data and beyond. In Proceedings of the International Joint Conference on Artificial Intelligence. 6125–6133 (2024).
Yang, Y. et al. SMNN: batch effect correction for single-cell RNA-seq data via supervised mutual nearest neighbor detection. Brief. Bioinforma. 22, bbaa097 (2021).
Zhou, X., Dong, K. & Zhang, S. Integrating spatial transcriptomics data across different conditions, technologies and developmental stages. Nat. Comput. Sci. 1–13 (2023).
Consortium, Hu. B. M. A. P. The human body at cellular resolution: the NIH Human Biomolecular Atlas Program. Nature 574, 187–192 (2019).
Xu, Z. et al. STOmicsDB: a comprehensive database for spatial transcriptomics data sharing, analysis and visualization. Nucleic Acids Res 52, D1053–D1061 (2024).
Bachmann, R., Mizrahi, D., Atanov, A. & Zamir, A. in European Conference on Computer Vision 348-367 (Springer, 2022).
Zenati, H., Foo, C. S., Lecouat, B., Manek, G. & Chandrasekhar, V. R. Efficient gan-based anomaly detection. arXiv preprint arXiv:1802.06222 (2018).
Zhu, J.-Y., Park, T., Isola, P. & Efros, A. A. in Proceedings of the IEEE International Conference on Computer Vision 2223-2232 (2017).
Li, X. et al. Deep learning enables accurate clustering with batch effect removal in single-cell RNA-seq analysis. Nat. Commun. 11, 2338 (2020).
Alquicira-Hernandez, J., Sathe, A., Ji, H. P., Nguyen, Q. & Powell, J. E. scPred: accurate supervised method for cell-type classification from single-cell RNA-seq data. Genome Biol. 20, 1–17 (2019).
De Kanter, J. K., Lijnzaad, P., Candelli, T., Margaritis, T. & Holstege, F. C. CHETAH: a selective, hierarchical cell type identification method for single-cell RNA sequencing. Nucleic Acids Res. 47, e95–e95 (2019).
Kiselev, V. Y., Yiu, A. & Hemberg, M. scmap: projection of single-cell RNA-seq data across data sets. Nat. Methods 15, 359–362 (2018).
Majidzadeh-A, K., Esmaeili, R. & Abdoli, N. TFRC and ACTB as the best reference genes to quantify Urokinase Plasminogen Activator in breast cancer. BMC Res. Notes 4, 1–7 (2011).
Zhang, X. et al. Thymosin beta 10 is a key regulator of tumorigenesis and metastasis and a novel serum marker in breast cancer. Breast Cancer Res. 19, 1–15 (2017).
De Falco, A., Caruso, F., Su, X.-D., Iavarone, A. & Ceccarelli, M. A variational algorithm to detect the clonal copy number substructure of tumors from scRNA-seq data. Nat. Commun. 14, 1074 (2023).
Gao, R. et al. Delineating copy number and clonal substructure in human tumors from single-cell transcriptomes. Nat. Biotechnol. 39, 599–608 (2021).
Korsunsky, I. et al. Fast, sensitive and accurate integration of single-cell data with Harmony. Nat. Methods 16, 1289–1296 (2019).
Johnson, W. E., Li, C. & Rabinovic, A. Adjusting batch effects in microarray expression data using empirical Bayes methods. Biostatistics 8, 118–127 (2007).
STAligner enables the integration and alignment of multiple spatial transcriptomics datasets. Nat. Comput. Sci. 3, 831–832 (2023).
Eguchi, J. et al. Interferon regulatory factors are transcriptional regulators of adipogenesis. Cell Metab. 7, 86–94 (2008).
Cronin, S. J., Woolf, C. J., Weiss, G. & Penninger, J. M. The role of iron regulation in immunometabolism and immune-related disease. Front. Mol. Biosci. 6, 116 (2019).
Haghverdi, L., Lun, A. T. L., Morgan, M. D. & Marioni, J. C. Batch effects in single-cell RNA-sequencing data are corrected by matching mutual nearest neighbors. Nat. Biotechnol. 36, 421–427 (2018).
Gulrajani, I., Ahmed, F., Arjovsky, M., Dumoulin, V. & Courville, A. C. Improved training of wasserstein gans. Advances in Neural Information Processing Systems. 30, 5769–5779 (2017).
Pang, M., Su, K. & Li, M. Leveraging information in spatial transcriptomics to predict super-resolution gene expression from histology images in tumors. bioRxiv, 2021.2011. 2028.470212 (2021).
Brody, S., Alon, U. & Yahav, E. in International Conference on Learning Representations (2021).
Xie, J., Girshick, R. & Farhadi, A. in International Conference on Machine Learning 478-487 (PMLR, 2016).
He, K., Zhang, X., Ren, S. & Sun, J. in Proceedings of the IEEE conference on computer vision and pattern recognition 770–778 (2016).
Wolf, F. A., Angerer, P. & Theis, F. J. SCANPY: large-scale single-cell gene expression data analysis. Genome Biol. 19, 1–5 (2018).
Svensson, V., Teichmann, S. A. & Stegle, O. SpatialDE: identification of spatially variable genes. Nat. Methods 15, 343–346 (2018).
Deng, T. et al. A cofunctional grouping-based approach for non-redundant feature gene selection in unannotated single-cell RNA-seq analysis. Brief. Bioinforma. 24, bbad042 (2023).
You, J., Ying, R., Ren, X., Hamilton, W. & Leskovec, J. in International Conference on Machine Learning 5708-5717 (PMLR, 2018).
Yu, X., Xu, X., Zhang, J. & Li, X. Batch alignment of single-cell transcriptomics data using deep metric learning. Nat. Commun. 14, 960 (2023).
Forrest, J. & Lougee-Heimer, R. in Emerging theory, methods, and applications 257-277 (INFORMS, 2005).
Zeira, R., Land, M., Strzalkowski, A. & Raphael, B. J. Alignment and integration of spatial transcriptomics data. Nat. Methods 19, 567–575 (2022).
Kaichen Xu, Y. L., et al. Xiaobo Sun Detecting anomalous anatomic regions in spatial transcriptomics with STANDS. STANDS. Zenodo, https://doi.org/10.5281/zenodo.13375297 (2024).
Acknowledgements
The project is funded by Strategic Priority Research Program of Chinese Academy of Sciences (Grant No. XDB38050100) to H.W. X.S. was supported by the startup grant from Zhongnan University of Economics and Law.
Author information
Authors and Affiliations
Contributions
X.S. conceived the idea and supervised the study. X.S. and K.X. designed the methodology and wrote the manuscript. X.S., K.X., Y.L., K.L., S.H., and Y.D. implemented the methods and conducted the experiments. K.X., X.S., and Y.L. summarized the results. K.X., M.H., and Y.L. collected the datasets required for the experiment. H.W., H.F. helped revise the manuscript. All authors have read and approved the final manuscript. Additionally, X.S. and K.X. contributed equally; Y.L. and S.H. contributed equally.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Communications thanks Juexin Wang and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. A peer review file is available.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Source data
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Xu, K., Lu, Y., Hou, S. et al. Detecting anomalous anatomic regions in spatial transcriptomics with STANDS. Nat Commun 15, 8223 (2024). https://doi.org/10.1038/s41467-024-52445-9
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-024-52445-9