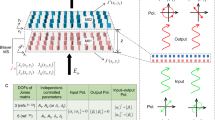
Abstract
On-chip metasurface for guided wave radiation works as an upgrade of conventional grating couplers, enriching the interconnection between guided wave and free-space optical field. However, the number of controllable parameters in equivalent Jones matrix of on-chip metasurface is limited that restricts the channels for multiplexing. Here, a supercell design based on detour phase and geometric phase has been proposed to reach full-parametric modulation of Jones matrix. As proof of concept, four independent sets of amplitude-phase channels have been experimentally demonstrated through a single on-chip metasurface. Moreover, through joint modulation of three phase mechanisms including detour phase, geometric phase and propagation phase, the Jones matrix could be decoupled from forward- and backward-propagating guided waves for direction multiplexing. This work paves the way for guided wave radiation towards high-capacity multiplexing and may further extend its application in optical communications, optical displays and augmented/virtual reality.
Similar content being viewed by others
Introduction
Composed of artificial nanostructures, metasurface has emerged as a revolutionary flat optical device to manipulate the optical field at subwavelength scale, including amplitude, phase, polarization and so on1,2,3. During the last decade, people have witnessed powerful optical meta-devices ranging from lens imaging, optical sensing, holographic display to quantum optics4,5,6,7,8,9,10,11. Owing to the multi-dimensional modulation capability, metasurface has demonstrated unparalleled advantages in numerous multiplexing technologies12,13,14,15,16,17,18,19. For polarization multiplexing, the optical response of metasurface could be described as a 2 × 2 equivalent Jones matrix, yet commonly with upper-limit of 6 independent parameters in free-space scenario20,21. To expand the number of multiplexed channels, bilayer metasurface22 and noise engineering23 were proposed from the perspective of spatial extension and algorithm optimization, which in turn usually need to sacrifice in fabrication convenience and signal-to-noise ratio (SNR) respectively.
On the other hand, photonic integrated circuit (PIC) promises a new information platform with more compact form with respect to the free space optical elements. Recently, metasurfaces have been incorporated with optical waveguides to elaborately tailor guided waves for extended functionalities and improved performance of photonic integrated devices24,25,26,27,28,29,30. In particular, on-chip metasurface can flexibly modulate the extracted guided waves as a remarkable upgrade of traditional couplers to enhance the far-field beam engineering31,32,33,34,35. Leveraging diverse phase modulation mechanisms, on-chip metasurface has been exploited in guided wave radiation to achieve beam focusing and deflection36,37, orbital angular momentum (OAM) beams38,39, holography40,41, etc. Owing to the on-chip optical propagation scheme, such guided wave driven metasurfaces are featured with no zero-order diffraction, which is promising for high-quality images in augment reality (AR) projection and optical displays42,43,44. In principle, resonant phase45 and propagation phase46,47 rely on the physical size of on-chip meta-atoms while geometric phase36,48 depends on the rotation angle to manipulate guided wave radiation. By taking advantage of the position distribution of meta-atoms, detour phase also provides a feasible solution to on-chip phase modulation49,50. Nevertheless, the limited degrees of freedom (DOFs) utilized in individual phase modulation mechanism inherently restrict the number of modulation channels. To address this issue, the combination of detour phase and geometric phase51,52, harmonic strategy (complex superposition of multiple phase profiles)48,53 and other mechanisms54 were proposed and attempted to improve the multiplexing capability. Despite of above endeavors in on-chip metasurfaces, the number of controllable parameters in equivalent Jones matrix is no more than 4 (See Table S1 in Supplementary Note 1), which does not reach the maximum yet. In addition, the advent of lithium niobate on insulator (LNOI) has propelled PICs as a promising platform to efficiently manage multiple DOFs of light at high speeds35,55,56.
Herein, we propose a strategy of on-chip metasurface design on LNOI platform to realize full-parametric modulation of Jones matrix for guided wave radiation. Through four-element supercell arrangement and combined modulation via detour phase and geometric phase, the symmetry and unitary of Jones matrix are broken and thus unlock the full four complex elements (i.e., 8 parameters). As an experimental demonstration, both the amplitude and phase of guided wave radiation under input guided waves propagating along x and y directions have been arbitrarily manipulated into four nano-printing and four holographic images in virtue of genetic algorithm optimization, as shown in Fig. 1. Moreover, to eliminate the conjugated effect induced in Jones matrices under two opposite propagating guided waves, propagation phase is additionally incorporated with detour phase and geometric phase to attain eight holographic images with respect to four illumination directions, resulting in two sets of direction-multiplexed Jones matrices in a single on-chip metasurface. On the basis of multiple phase modulation mechanisms, such on-chip metasurface design offers a platform for guided wave manipulation with high multiplexing capacity and may trigger broader applications in on-chip optical field manipulation.
The generated nano-printing and holographic images under TE0 guided wave illuminations along y (blue) and x (magenta) directions are featured with polarization properties indicated by white double arrows. The inset indicates the perspective view of the corresponding four-element supercell m1, m2, m3 and m4 based on detour phase and geometric phase.
Results
Design of on-chip metasurface
As depicted in Fig. 2a, the on-chip metasurface for guided wave radiation is comprised of silicon nanopillars arranged with periods of Px and Py along x and y directions on the substrate of x-cut LNOI. A 100 nm spacing layer of silicon dioxide is placed between LN waveguide and silicon metasurface to ensure weak interaction process. The variables of nanopillar include the two-dimensional position displacements δx and δy, rotation angle θ and geometric size of length L and width W (with a fixed height H of 1.2 μm). It should be noted that the definition of Jones matrix for on-chip metasurface is different from that for free-space metasurface. For on-chip scheme, guided wave illuminations along x and y directions could inherently introduce detour phase as two additional modulation DOFs, which breaks the limitation in modulation of Jones matrix. To this end, we define the input TE0 modes propagating along y and x directions, which are equivalent to a pair of orthogonal polarization states, as two bases of Jones matrix for on-chip metasurface. Assuming that a TE0 mode propagating y (x) direction with polarization \({[\begin{array}{cc}1 & 0\end{array}]}^{T}\)(\({[\begin{array}{cc}0 & 1\end{array}]}^{T}\)) is excited in slab lithium niobate (LN) waveguide, the extracted radiation can be written as \({[\begin{array}{cc}{J}_{xx} & {J}_{xy}\end{array}]}^{T}\)(\({[\begin{array}{cc}{J}_{yx} & {J}_{yy}\end{array}]}^{T}\)). Here, Jxx and Jxy (Jyx and Jyy) are the complex elements of equivalent Jones matrix J of on-chip metasurface described as follows
a The schematic diagram of one nanopillar for Jones matrix modulation driven by guided waves along y (blue) and x (magenta) directions. The simulated detour phase ϕD and geometric phase ϕPB induced by (b) in-plane displacement δx, δy and c rotation angle θ of nanopillar. The solid lines represent the fitting lines. d The top view of the four-element supercell composed of m1, m2, m3 and m4 based on detour phase and geometric phase with period of 2Px and 2Py. e, f The phase responses ϕx and ϕy as a function of the length and width of nanopillar under guided waves propagating along y and x directions. g The illustration of the four-element supercell based on detour phase, geometric phase and propagation phase.
To modulate the parameters of Jones matrix, we first investigate the detour phase and geometric phase induced by on-chip metasurface through numerical simulations (See Methods). With Py of 760 nm and Px of 790 nm, equal to the effective wavelengths of TE0 guided modes along y and x direction at 1550 nm, the phase shifts caused by detour phase ϕD linearly vary with the position displacements δx and δy of nanopillar for input guided modes along x and y directions (Fig. 2b). As shown in Fig. 2c, the phase shifts ϕPB of left-handed circularly polarized (LCP) and right-handed circularly polarized (RCP) radiations follow the relationship of ±2θ with rotation angle under input RCP and LCP guided modes. For such on-chip anisotropic nanopillars with C2-symmetry, individual detour phase contributes to a symmetric Jones matrix with only two independent elements Jxx and Jyy, and geometric phase for one element Jxx, see Eqs. (S2) and (S3). Through combining detour phase and geometric phase, the Jones matrix could be expressed as
Here, ax0, ay0 and ϕx0, ϕy0 are the fixed amplitude and phase responses from nanopillar’s propagation phase with L = 300 nm and W = 100 nm under guided wave illuminations along y and x directions, R(±θ) is the rotation matrix. It should be noted that the above Jones matrix is asymmetric (Jxy≠Jyx) since the rotation symmetry within one pixel is broken by introducing position displacements (namely detour phase), which results in two non-diagonal terms decoupled. Nevertheless, the Jones matrix is nearly unitary (See Supplementary Note 2.1) and it leads to the four elements of Jones matrix interrelated, that is \({J}_{xx}\cdot {J}_{xy}^{\ast }+{J}_{yx}\cdot {J}_{yy}^{\ast }=0\) (* represents complex conjugation). Such unitary condition constraints the independent modulation channels no more than six. To construct a non-unitary Jones matrix, a practical way is to establish supercell design using interference effect of meta-atoms, which has been investigated in free-space metasurfaces57,58,59. In view of this, a four-element supercell design with period of 2Py = 1520 nm and 2Px = 1580 nm presented in Fig. 2d is introduced for full-parametric modulation and the equivalent Jones matrix can be derived in summation of four matrices as below
where k is the sequence of the nanopillar in a four-element supercell. With coherent superposition of four unitary Jones matrices of single nanopillar expressed by Eq. (2), the above constructed Jones matrix of supercell turns into non-unitary (See Supplementary Note 2.1) and it means the full complex elements (Jxx, Jxy, Jyx and Jyy) are totally unlocked for full-parametric modulation. From the perspective of geometric arrangement, the asymmetric and non-unitary of Jones matrix arise from the induced C2-symmetry breaking and the interference effect by four-element supercell based on detour phase and geometric phase.
To map each parameter of Jones matrix into the physical model of on-chip metasurface, a group of complex equations are required to be solved according to Eq. (3). Hence, we establish eight complex equations to acquire four sets of amplitude-phase channels for full-parametric modulation of Jones matrix, shown in Eqs. (S7). It is worth mentioning that the separation between each nanopillar should be large enough to avoid spatial overlapping and strong coupling, a set of constraint conditions on spatial arrangement of nanopillars is assigned as inequalities S8 (See Supplementary Note 3). Herein, the variables of nanopillars in each supercell are determined by solving the complex equations using genetic algorithm optimization, as detailed in the flow chart in Fig. S2. Owing to the sufficient variables provided in the proposed four-element supercell design (12 variables for full-parametric modulation), the complex Eqs. (S7) are accessible to be solved for arbitrary desired parameters of Jones matrix. By means of the above optimization for all the supercells, four amplitude-phase images have been successfully reconstructed with negligible deviation shown in Fig. S5a. To validate the accuracy of the above theory expressed by Eq. (3), full-wave numerical simulations have been performed. The simulated results presented in Supplementary Note 4 are in agreement with the optimized results through genetic algorithm, which verifies the feasibility of full-parametric modulation based on supercell design.
Demonstration for full-parametric modulation of Jones matrix
As experimental demonstrations, we fabricated the designed on-chip metasurface configuration through the preparation process detailed in Methods. Figures 3a, b display the optical microscope and scanning electron microscope (SEM) images of metasurface for full-parametric modulation, respectively. The green dashed box in Fig. 3b highlights one fabricated four-element supercell where each element is featured with the same geometric size of L = 300 nm and W = 100 nm. To excite the guided modes at 1550 nm along y and x directions in experiments, four silicon grating couplers surrounding the on-chip metasurface are prepared on top of LN slab waveguide with a silicon dioxide cladding layer. Once the on-chip metasurface is illuminated, the guided wave radiations are characterized by the measurement setup detailed in Supplementary Note 5. Figure 3c lists the four sets of nano-printing and holographic images recorded in the objective plane and Fourier plane respectively. As exhibited in the first column, the guided wave along y direction (input x-polarization) is extracted to display a nano-printing letter “χ” and a holographic image “C” after passing through x-polarization analyzer, corresponding to the complex element Jxx of Jones matrix. By rotating the analyzer to y-polarization, the nano-printing image shows another letter “β” while the holographic image turns into “A” in the second column, which represents the modulation of Jxy. When switching the propagation direction to x direction, another two nano-printing letters “η” and “ε” along with two holographic images “H” and “D” are presented in the third and fourth columns. The above eight independent channels verify the full-parametric Jones matrix modulation capability of single-layer on-chip metasurface. Here, the extraction efficiency of the on-chip metasurface, which is defined as the ratio of the power of the generated holographic images to the power of input guided waves, is experimentally measured to be ~6.5%. In addition, there is no constraint on the output polarization and an arbitrary set of two output polarization states has been achieved in Supplementary Note 6.
a Optical microscope image of the fabricated silicon metasurface surrounded by four grating couplers (only three shown) on LNOI substrate. Scale bar: 200 μm. GC: grating coupler. MS: metasurface. b Scanning electron microscope image of the on-chip metasurface. The green dashed box outlines one supercell. Scale bar: 1 μm. c Measured four sets of nano-printing and holographic images related to four elements of Jones matrix Jxx, Jxy, Jyx and Jyy. The white arrows in the bottom left and right corner indicate the polarization states of input guided waves and output analyzers, respectively.
Direction-multiplexed modulation of Jones matrix
Although above supercell design based on detour phase and geometric phase has validated the feasibility of full-parametric modulation, the propagation direction of guided wave remains to be explored for multiplexing. According to the Eq. (3), the Jones matrix J+ of on-chip metasurface for forward-propagating guided waves is a complex conjugate of J- for backward-propagating guided waves, which disables the functionality of direction-multiplexed modulation. Such conjugated relation has been validated in Supplementary Note 7. To make a step further, we additionally introduce propagation phase to incorporate with detour phase and geometric phase to acquire direction-multiplexed modulation of Jones matrix, as illustrated in Fig. 4a. Figures 2e, f plot the simulated phase response maps ϕx and ϕy of extracted light with the length and width of single nanopillar for guided waves propagating along y and x directions, respectively (The amplitude response maps ax and ay can be obtained from the extracted efficiency Tx and Ty given in Fig. S1). As exhibited in Fig. 2g, based on three phase mechanisms, the on-chip metasurface featured with supercell design could demonstrate the following direction-multiplexed modulation of Jones matrices
a Schematic of on-chip metasurface based on detour phase, geometric phase and propagation phase under guided wave illuminations along +x (magenta), +y (blue), -x (red) and –y (light blue) directions. The inset indicates the perspective view of the four-element supercell. b, c Top and side view of the fabricated on-chip metasurface. The green dashed box highlights one four-element supercell. Scale bars: 1 μm. d Measured eight holographic images under different propagation directions and polarization states of analyzers, corresponding to eight elements of J±. The white one-way arrows represent the propagation directions of guided waves while the double arrows indicate the output polarization states.
Here, ± denotes the propagation direction of guided waves (+ for +x and +y directions while – for -x and -y directions). axk, ayk and ϕxk, ϕyk are the amplitude and phase responses of induced propagation phase by the k-th naopillar in supercell. The introduction of propagation phase gives rise to the breaking of conjugated relation between J+ and J-, i.e., \({J}_{+}\ne {J}_{-}^{\ast }\) (See Eq. (S6) in Supplementary Note 2.2). Considering that the above direction-dependent Jones matrices are asymmetric and non-unitary, eight elements of two sets of Jones matrices (J±xx, J±xy, J±yx, J±yy) could be engineered at will. Based on Eq. (4), eight phase-only modulation channels are designed to confirm the direction-multiplexed modulation capability by selecting variables of four-element supercells through genetic algorithm optimization shown in Supplementary Note 3 with optimized results listed in Fig. S6a. The validity of such direction-multiplexed modulation design has been confirmed through numerical simulations, as plotted in Fig. S6b. Figures 4b, c showcase the top and side view of the fabricated sample, respectively. As captured in Fig. 4d, the holographic images exhibit four letters “HOLO” under input guided waves along y and x directions while another four different holographic images “GRAM” are demonstrated for guided waves along -y and -x directions when switching the polarization states of analyzer. The conjugacy of two equivalent Jones matrices J+ and J- has been totally broken and it contributes to the eight direction-multiplexed phase modulation channels.
Discussion
To conclude, an on-chip metasurface design strategy for multi-channel modulation of guided wave radiation has been proposed on the basis of joint phase modulation mechanism and supercell arrangement. By virtue of detour phase and geometric phase, such on-chip metasurface can perform full-parametric modulation of equivalent Jones matrix and the corresponding four sets of amplitude and phase channels have been experimentally demonstrated. Furthermore, attributed to the combination of detour phase, geometric phase and propagation phase, the equivalent Jones matrices under forward- and backward-propagating guided wave illuminations are decoupled for direction-multiplexed modulation. As an outlook, our approach for Jones matrix modulation is compatible with other strategies (e.g., harmonic strategy or phase optimization) to further increase the number of modulation channels and improve the multiplexing capability (See Supplementary Note 8). Also, since the on-chip metasurface is implemented on LNOI platform, a range of dynamic guided wave radiation device could be expected due to the distinctive electro-optic property of LN. Our work offers a compelling choice for on-chip information multiplexing and may inspire a plethora of intriguing multifunctional photonic integrated devices.
Methods
Numerical simulations
The phase response of nanopillar was investigated by numerical simulations via finite-difference time domain (FDTD) methods. For detour phase and propagation phase models, the silicon nanopillars were periodically arranged along y direction (x direction) with Py = 760 nm (Px = 790 nm) on top of a 20 μm-length x-cut LN waveguide with a 100 nm silicon dioxide cladding layer. The 1550 nm TE0 mode source propagating along y direction (x direction) was excited in 600 nm-thick LN waveguide to illuminate nanopillars. Periodic boundary condition was applied along x direction (y direction) while perfectly matched layer (PML) conditions were utilized as boundary conditions along y and z directions (x and z directions). For geometric phase model, to synthesize in-plane LCP and RCP modes, two TE0 mode sources propagating along y and x directions with phase difference of ±π/2 were simultaneously excited and all the boundary conditions were chosen to be PML. The refractive indexes of x-cut LN, silicon dioxide and silicon used in simulations were obtained from experimental samples measured by spectroscopic ellipsometer.
Device fabrication
The samples were fabricated on a commercial x-cut LNOI wafer with 600 nm thick LN layer and 2.0 μm thick buried silicon dioxide. As a first step, a 100 nm silicon dioxide layer and a α-Si layer with a thickness of 1.2 μm were successively deposited on top of LN substrate through plasma-enhanced chemical vapor deposition (PECVD). After spin-coating a 200 nm-thick electron beam resist (PMMA-A4) on α-Si layer, the patterns of on-chip metasurface and grating couplers were defined by Electron-beam lithography (EBL) system (ELS-F125, Elionix). Then, the generated patterns were transferred to an electron beam evaporated chromium layer after development, which served as a hard mask for the following dry etching process of α-Si layer in a mixture of C4F8 and SF6 plasma (HSE200, Naura). At last, the remaining chromium mask was removed by ammonium cerium nitrate.
Data availability
The data that support the findings of this study are provided in the Supplementary Information/ Source Data file. Source data are provided with this paper.
References
Yu, N. et al. Light Propagation with Phase Discontinuities: Generalized Laws of Reflection and Refraction. Science 334, 333–337 (2011).
Chen, W. T., Zhu, A. Y. & Capasso, F. Flat optics with dispersion-engineered metasurfaces. Nat. Rev. Mater. 5, 604–620 (2020).
Li, T. et al. Revolutionary meta-imaging: from superlens to metalens. Photonics Insights 2, R01 (2023).
Wang, S. et al. Broadband achromatic optical metasurface devices. Nat. Commun. 8, 187 (2017).
Wang, S. et al. A broadband achromatic metalens in the visible. Nat. Nanotechnol. 13, 227–232 (2018).
Ye, X. et al. Chip-scale metalens microscope for wide-field and depth-of-field imaging. Adv. Photonics 4, 046006 (2022).
Zhang, S. et al. Metasurfaces for biomedical applications: imaging and sensing from a nanophotonics perspective. Nanophotonics 10, 259–293 (2020).
Qin, J. et al. Metasurface Micro/Nano-Optical Sensors: Principles and Applications. ACS Nano 16, 11598–11618 (2022).
Jiang, Q., Jin, G. & Cao, L. When metasurface meets hologram: principle and advances. Adv. Opt. Photonics 11, 518–576 (2019).
Stav, T. et al. Quantum entanglement of the spin and orbital angular momentum of photons using metamaterials. Science 361, 1101–1104 (2018).
Li, L. et al. Metalens-array–based high-dimensional and multiphoton quantum source. Science 368, 1487–1490 (2020).
Arbabi, A., Horie, Y., Bagheri, M. & Faraon, A. Dielectric metasurfaces for complete control of phase and polarization with subwavelength spatial resolution and high transmission. Nat. Nanotechnol. 10, 937–943 (2015).
Ye, W. et al. Spin and wavelength multiplexed nonlinear metasurface holography. Nat. Commun. 7, 11930 (2016).
Leitis, A. et al. Angle-multiplexed all-dielectric metasurfaces for broadband molecular fingerprint retrieval. Sci. Adv. 5, eaaw2871 (2019).
Yang, H. et al. Angular momentum holography via a minimalist metasurface for optical nested encryption. Light Sci. Appl. 12, 79 (2023).
Guo, Y. et al. Spin-decoupled metasurface for simultaneous detection of spin and orbital angular momenta via momentum transformation. Light Sci. Appl. 10, 63 (2021).
Zhang, F. et al. Meta-optics empowered vector visual cryptography for high security and rapid decryption. Nat. Commun. 14, 1946 (2023).
Li, X. et al. Time-sequential color code division multiplexing holographic display with metasurface. Opto-Electron. Adv. 6, 220060–220060 (2023).
Nan, T. et al. Generation of structured light beams with polarization variation along arbitrary spatial trajectories using tri-layer metasurfaces. Opto-Electron. Sci. 3, 230052–230052 (2024).
Bao, Y., Wen, L., Chen, Q., Qiu, C.-W. & Li, B. Toward the capacity limit of 2D planar Jones matrix with a single-layer metasurface. Sci. Adv. 7, eabh0365 (2021).
Feng, C. et al. Diatomic Metasurface for Efficient Six‐Channel Modulation of Jones Matrix. Laser Photonics Rev. 17, 2200955 (2023).
Bao, Y. et al. Observation of full-parameter Jones matrix in bilayer metasurface. Nat. Commun. 13, 7550 (2022).
Xiong, B. et al. Breaking the limitation of polarization multiplexing in optical metasurfaces with engineered noise. Science 379, 294–299 (2023).
Li, Z. et al. Controlling propagation and coupling of waveguide modes using phase-gradient metasurfaces. Nat. Nanotechnol. 12, 675–683 (2017).
Wang, Z. et al. On-chip wavefront shaping with dielectric metasurface. Nat. Commun. 10, 3547 (2019).
Meng, Y. et al. Versatile on-chip light coupling and (de)multiplexing from arbitrary polarizations to controlled waveguide modes using an integrated dielectric metasurface. Photonics Res 8, 564 (2020).
Kim, I. et al. Nanophotonics for light detection and ranging technology. Nat. Nanotechnol. 16, 508–524 (2021).
Meng, Y. et al. Optical meta-waveguides for integrated photonics and beyond. Light Sci. Appl. 10, 235 (2021).
Wu, C. et al. Programmable phase-change metasurfaces on waveguides for multimode photonic convolutional neural network. Nat. Commun. 12, 96 (2021).
Wang, Z. et al. Metasurface on integrated photonic platform: from mode converters to machine learning. Nanophotonics 11, 3531–3546 (2022).
Zhou, N. et al. Ultra-compact broadband polarization diversity orbital angular momentum generator with 3.6 × 3.6 μm2 footprint. Sci. Adv. 5, eaau9593 (2019).
Guo, X., Ding, Y., Chen, X., Duan, Y. & Ni, X. Molding free-space light with guided wave–driven metasurfaces. Sci. Adv. 6, eabb4142 (2020).
Wang, Z. et al. Metasurface empowered lithium niobate optical phased array with an enlarged field of view. Photonics Res 10, B23–B29 (2022).
Wang, Z. et al. On-chip integration of metasurface-doublet for optical phased array with enhanced beam steering. Nanophotonics 12, 2425–2432 (2023).
Zhong, H. et al. Gigahertz-rate-switchable wavefront shaping through integration of metasurfaces with photonic integrated circuit. Adv. Photonics 6, 016005 (2024).
Fang, B., Wang, Z., Gao, S., Zhu, S. & Li, T. Manipulating guided wave radiation with integrated geometric metasurface. Nanophotonics 11, 1923–1930 (2021).
Xie, C. et al. Bifocal focusing and polarization demultiplexing by a guided wave-driven metasurface. Opt. Express 29, 25709–25719 (2021).
Ha, Y. et al. Monolithic‐Integrated Multiplexed Devices Based on Metasurface‐Driven Guided Waves. Adv. Theory Simul. 4, 2000239 (2021).
Ji, J. et al. Metasurface-Enabled On-Chip Manipulation of Higher-Order Poincare Sphere Beams. Nano Lett. 23, 2750–2757 (2023).
Shi, Y. et al. On-chip meta-optics for semi-transparent screen display in sync with AR projection. Optica 9, 670–676 (2022).
Liu, Y., Shi, Y., Wang, Z. & Li, Z. On-Chip Integrated Metasystem with Inverse-Design Wavelength Demultiplexing for Augmented Reality. ACS Photonics 10, 1268–1274 (2023).
Li, Z., Shi, Y., Dai, C. & Li, Z. On-Chip‐Driven Multicolor 3D Meta‐Display. Early view at https://doi.org/10.1002/lpor.202301240 (2024).
Shi, Y. et al. Electrical-Driven Dynamic Augmented Reality by On-Chip Vectorial Meta-Display. ACS Photonics 11, 2123–2130 (2024).
Wan, S. et al. Multidimensional Encryption by Chip-Integrated Metasurfaces. ACS Nano 18, 18693–18700 (2024).
Ding, Y. et al. Metasurface-Dressed Two-Dimensional on-Chip Waveguide for Free-Space Light Field Manipulation. ACS Photonics 9, 398–404 (2022).
Hsieh, P.-Y. et al. Integrated metasurfaces on silicon photonics for emission shaping and holographic projection. Nanophotonics 11, 4687–4695 (2022).
Hsieh, P. Y. et al. Metasurfaces on silicon photonic waveguides for simultaneous emission phase and amplitude control. Opt. Express 31, 12487–12496 (2023).
Fang, B. et al. Spin-decoupled meta-coupler empowered multiplexing and multifunction of guided wave radiation. Photonics Res 11, 2194–2201 (2023).
Yang, R. et al. Immersive Tuning the Guided Waves for Multifunctional On‐Chip Metaoptics. Laser Photonics Rev. 16, 2200127 (2022).
Shi, Y. et al. On-Chip Meta-Optics for Engineering Arbitrary Trajectories with Longitudinal Polarization Variation. Nano Lett. 24, 2063–2070 (2024).
Shi, Y. et al. Augmented Reality Enabled by On‐Chip Meta‐Holography Multiplexing. Laser Photonics Rev. 16, 2100638 (2022).
Fang, B. et al. On-chip non-uniform geometric metasurface for multi-channel wavefront manipulations. Opt. Lett. 48, 3119–3122 (2023).
Li, Z. et al. On‐Chip Direction‐Multiplexed Meta‐Optics for High‐Capacity 3D Holography. Adv. Funct. Mater. 34, 2312705 (2024).
Huang, H. et al. Leaky-wave metasurfaces for integrated photonics. Nat. Nanotechnol. 18, 580–588 (2023).
Zhu, D. et al. Integrated photonics on thin-film lithium niobate. Adv. Opt. Photonics 13, 242–352 (2021).
Boes, A. et al. Lithium niobate photonics: Unlocking the electromagnetic spectrum. Science 379, eabj4396 (2023).
Liu, M. et al. Multifunctional metasurfaces enabled by simultaneous and independent control of phase and amplitude for orthogonal polarization states. Light Sci. Appl. 10, 107 (2021).
Chen, C. et al. Bifacial-metasurface-enabled pancake metalens with polarized space folding. Optica 9, 1314–1322 (2022).
Deng, Z. L. et al. Full‐Color Complex‐Amplitude Vectorial Holograms Based on Multi‐Freedom Metasurfaces. Adv. Funct. Mater. 30, 1910610 (2020).
Acknowledgements
The authors acknowledge the funding provided by National Key Research and Development Program of China (No. 2022YFA1404301 (T.L.)), National Natural Science Foundation of China (Nos. 62325504 (T.L.), 62305149 (C.C.), 92250304 (T.L.), 62288101 (T.L.)), and Dengfeng Project B of Nanjing University (T.L.). The authors acknowledge the micro-fabrication center of the National Laboratory of Solid State Microstructures (NLSSM) for technique support.
Author information
Authors and Affiliations
Contributions
J.J., Z.W. and T.L. conceived the concept. J.J., X.L. and J.W. proposed the metasurface design and performed the numerical simulations; J.L. and J.S. fabricated the samples; J.J. performed the optical measurements with the help of J.W. and X.Y.; J.J., Z.W., B.F., C.C., T.L. and S.Z. discussed the results; J.J. and Z.W. wrote the manuscript; T.L. supervised the project.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Communications thanks Xian-Gang Luo and the other anonymous reviewer(s) for their contribution to the peer review of this work. A peer review file is available.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Source data
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Ji, J., Li, J., Wang, Z. et al. On-chip multifunctional metasurfaces with full-parametric multiplexed Jones matrix. Nat Commun 15, 8271 (2024). https://doi.org/10.1038/s41467-024-52476-2
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-024-52476-2
This article is cited by
-
All-dielectric meta-waveguides for on-chip integration
npj Nanophotonics (2025)
-
Creating topological exceptional point by on-chip all-dielectric metasurface
Light: Science & Applications (2025)
-
Spectral convolutional neural network chip for in-sensor edge computing of incoherent natural light
Nature Communications (2025)
-
Dynamic holographic display with addressable on-chip metasurface network based on lithium niobate photonics
Light: Science & Applications (2025)