Introduction

Water under pressure is both ubiquitous in natural phenomena and a complex system. The quasi-static pressure exploration of H2O phase diagram, under various temperatures, has revealed a rich polymorphism, with 19 crystalline forms of ice identified so far1,2. Ice VII is a prominent phase occupying a large region of the phase diagram at pressures above 2 GPa and having the simplest crystallographic unit cell with a body-centered cubic oxygen sublattice and a proton disordered arrangement3,4. Ice VII is believed to play an important role in the physics of outer planetary bodies5 and it is now considered a mineral as it has been recovered from the earth mantle as a diamond inclusion6. Understanding the structural changes of water under rapid temperature or pressure variation is a topic of current focus7,8, with the observation of metastable phases and implication to impact events on planetary icy bodies. On one hand, rapid cooling of H2O below its glass transition temperature of 136 K yields an amorphous phase known as low-density amorphous (LDA) ice9. A High density amorphous (HDA) ice has also been observed under pressure and the transition between LDA and HDA was speculated to be consistent with the existence of a liquid-liquid transition in supercooled water10,11. However this analogy is still a matter of ongoing debate12,13. The true H2O liquid-liquid transition could be recently observed by fast isochoric heating of a quenched HDA sample at ambient pressure14. On the other hand, many studies have investigated rapidly compressed water. Quasi-isentropic pressure loading platforms, using laser drives7,15, magnetic drives16,17 and gas guns18 have been used to investigate the freezing kinetics in over-compressed water. Loading pressure times within the nanosecond timeframe, associated to compression rate covering two orders of magnitude over the different platforms, could then be investigated. Liquid water was observed to persist up to 8 GPa, well into the stability field of ice VII and a freezing into ice VII was therefore speculated. The effects of loading pressure within the millisecond range were investigated using the dynamical diamond anvil cell (d-DAC)19,20,21. The corresponding compression rates could over-compress liquid water up to approximately 2 GPa at most. Freezing into ice VII in the stability field of ice VI was first suspected19, then evidence of HDA was presented20 and finally evidence of a mixture between ice VI and HDA was shown21. It should be noted that none of these dynamic studies could unambiguously resolve the freezing mechanism of metastable water, due to the absence of a time-resolved microscopic diagnostic. The present study aims to elucidate, at the microscopic level, the solidification process of metastable water under dynamic compression. In particular, we are investigating whether the freezing state of metastable water at high compression rates above 2 GPa is indeed ice VII or a metastable structure, and why the transition sequence reverses compared to rapid cooling, i.e. with an amorphous phase at low compression rates and a crystalline phase at high compression rates. Additionally, we aim to consistently interpret the observations across the entire range of compression rates accessible, using d-DAC on one end to gas-gun/laser compression on the other end. To better bridge the gap between static compression and nanosecond-dynamic compression, the d-DAC technique has been optimized to achieve a pressure rise time of about 0.1 ms, allowing four orders of compression rates to be covered on the same d-DAC platform. Structural microscopic changes along the compression path were monitored using time-resolved X-ray diffraction (XRD), complemented by optical imaging and pressure luminescence measurements, all with framing steps down to a few microseconds.

Results

Instrumentation

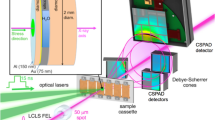
The experimental setup, depicted in Fig. 1, comprises a piezoactuated d-DAC along with three real-time event monitoring diagnostics: X-ray diffraction, pressure luminescence measurements, and optical imaging. The DAC serves as the primary tool for static high-pressure experiments. Leveraging diamond’s remarkable transparency across the electromagnetic spectrum, light is utilized to extract properties of the compressed samples. Typically, detailed characterizations of sample properties under pressures up to 100 GPa are conducted, employing primarily synchrotron X-ray diffraction completed by spectroscopy methods over the infra-red to X-ray excitation range22. Recently, this characterization has been extended to the TPa range23. The concept of operating the DAC dynamically was proposed in 2007, employing voltage-driven piezoactuators to generate pressure19,24. Subsequently, pressure rise times in the 10 ms range were demonstrated, particularly in the study of water20,21. An improved design employing a hollow cylinder piezoactuator has been proposed, offering access to sub-millisecond rise times25. Our d-DAC is based on a similar design. As illustrated in Fig. 1, the sample pressure response in the sample follows the tailored voltage applied to the piezoactuator. Pressure rise times as fast as 100 μs can be achieved. Importantly, the experimental conditions maintain close proximity to isothermal compression, facilitated by the high thermal conductivity of diamond anvils26. The equilibration time of pressure in the sample is estimated to be less than 1 μs, derived from the reverberation time of compressive waves propagating at the sample’s sound velocity across the chamber. The d-DAC retains the optical access of a standard DAC. The primary challenge in detailed measurements during dynamic compression has been to follow the sample’s properties with sufficiently small time steps. d-DAC compression experiments initially relied on ms-time resolved micro-photography, ruby luminescence pressure measurement, and Raman spectroscopy19,20,21. Time-resolved X-ray diffraction measurements in the d-DAC became feasible using the high brilliance, high flux X-ray beams from third-generation synchrotron sources and by the emergence of large hybrid pixel array detectors with very short readout times, such as the EIGER27 and LAMBDA25 detectors. Angular X-ray diffraction patterns at repetition rates up to 4 kHz have been reported25. In the present study, diffraction patterns at a maximum repetition rate of 250 kHz could be achieved, benefiting significantly from the high flux at 19 KeV in front of the ID09 beamline of the EBS-ESRF synchrotron28 and the operation of the JUNGFRAU detector in burst mode (limited to 16 images)29. Pressure luminescence measurements and imaging of the sample could be performed within a similar timeframe, though not simultaneously with XRD. Typical XRD patterns and luminescence spectra are shown in Fig. 1. The pressure was measured using the samarium-doped strontium borate (SrB4O7 : Sm2+) luminescence pressure gauge30 and using XRD data from the Birch–Murnaghan equation of state (EoS) of ice VII31 and the Vinet EoS of Cu32 or Sn33. The pressure was determined using a luminescence gauge during imaging and by utilizing XRD equation-of-state (EOS) data during XRD. The results from the different pressure measurement methods were found to be highly consistent with each other. A high reproducibility of the sample pressure evolution under a given piezoactuator voltage function acting on the piston of the d-DAC is observed.

Fig. 1: Dynamic-DAC experimental setup.
figure 1

a Schematic of the experimental configuration. X-ray diffraction spectra are recorded as a function of time on a JUNGFRAU 1M detector in a Debye–Scherrer geometry (b) and are azimuthaly integrated into an XRD pattern where the diffraction peaks of ice VII are clearly measured in 20 μs (c). SrB4O7 : Sm2+ fluorescence over time is recorded on an iXon EMCCD (d) alongside images on a Photron Fast Camera. A typical system pressure response (red) to the input voltage (blue) are plotted versus time (e).

Full size image

Pressure response of water under compression ramps

By applying a step load function on the piezo-actuator of the d-DAC, the pressure is expected to undergo a three-stage evolution: initially a gradual increase in pressure, followed by a rapid linear rise, and reaching a plateau. However, if a phase transition occurs, the pressure rise is disrupted by the pressure drop associated to the negative volume discontinuity at the transition, resulting in an apparent negative compressibility. This phenomenon is depicted in Fig. 2 and in Supplementary Fig. 2 (see Supplementary Materials) when compressing water from its liquid phase across the stability domains of ice VI and ice VII. In Supplementary Fig. 2, with a compression rate of  ~ 0.1 GPa/ms, two events are observed: the first one associated with the crystallization of water into ice VI and the second with the structural transition of ice VI into ice VII. If the over-compression of the low-pressure phase within the stability field of the high-pressure phase is not excessive, the pressure drop aligns with the pressure of the phase transition. A pressure plateau at the melting pressure is even observed if the compression rate is slower than the crystal growth rate. As depicted in Fig. 2, when crystallization occurs at higher compression rates (≥0.4 GPa/ms), the pressure drops to 1.6 GPa, followed by the observation of a pressure plateau. Time-resolved photo-micrographs correlate optical changes in the sample with deviations from the expected linear pressure rise. These deviations begin when an homogeneous nucleation occurs, while the subsequent plateau at 1.6 GPa corresponds to crystal growth. Once the sample chamber is again filled with an ice crystal, a linear pressure rise resumes, with no further pressure rise anomalies observed. Notably, the solid-liquid equilibrium at 1.6 GPa corresponds to the melting point of ice VII (obtained from the melting curve of ice VII metastably extended below the Ice VI-ice VII-liquid triple point, see Supplementary Materials). Similarly, a stress release phenomenon, resulting from the interplay of compression and phase transition, was noted in the VISAR traces of the ns-dynamical quasi-isentropic compression experiments7,16,17,18, being interpreted as the signature of a phase transition. This characteristic was termed a kinetic van der Waals loop16. Its observation implied that a first order phase transition was taking place, even for the highest compression rate achieved with laser shocks, thus ruling out the transformation of super-compressed water into an amorphous phase via a glass phase transition. It was suggested that crystallization occurs into ice VII, although without time-resolved XRD measurements this proposition remains to be proven.

Fig. 2: Dynamic compression of liquid water at 0.4 GPa/ms.
figure 2

The sample pressure over time is measured using the SrB4O7 : Sm2+-chip fluorescence while micro-photographs are recorded at 40 kHz framing time. Errors bars are estimated to be  ±0.05 GPa following30 and our system sensitivity. At the liquid-solid phase transition a characteristic pressure drop due the density difference is observed. Visual observation with the ultra-fast camera reveals a homogeneous nucleation in the sample volume. The over-compression pressure, ΔP, is defined as the pressure differential between crystallization and the associated ice VII melting at the same temperature (1.56 GPa). The quantity Δt represents the corresponding duration over which fluid water remains in its metastable state.

Full size image

In this study, over-compressed water has been investigated for various compression ramps, ranging from 0.1 ms to 20 ms in pressure rise time. The compression peak was maintained below 20 GPa, so the associated compression rates varied from 0.4 GPa/ms to 110 GPa/ms. The solidification of metastable water into ice VII was always observed by time resolved XRD. Figure 3 displays typical pressure responses of the water sample for two measurements conducted at slow and fast compression rates. Sample pressure-versus-time evolution for each compression was consistently measured using various pressure gauges: X-ray diffraction of a small metal flake (Sn or Cu) embedded in water, using their Vinet Equation of State (EoS)32,33; XRD volume of ice VII post metastable water crystallization, using the Birch–Murnaghan EoS of ice VII31; and the strontium-doped-borate luminescence gauge30. An excellent agreement between the different pressure determinations was observed, along with high reproducibility of the pressure evolution. In all time-resolved compression ramps, a disruption in the pressure rise is observed correlated to the nucleation of metastable water to ice VII, as evidence by the appearance of XRD (110) and (111) peaks of ice VII. At low compression rates, a kinetic pressure loop with apparent negative compressibility can be noted while at higher rates, this feature transitions more towards a slope rupture, probably because the framing time of the measurements is too long to capture the pressure dip.

Fig. 3: Measured pressure as a function of time for compression rates of 1.6 GPa/ms and 110 GPa/ms.
figure 3

At the freezing pressure into ice VII, a rupture in the compression slope is observed due to the negative discontinuity at crystallization. Pressure is measured using the SrB4O7 : Sm2+ fluorescence gauge and in some cases using the volume of a piece of Cu embedded in the sample chamber. The freezing into ice VII is evidenced from the XRD pattern. After freezing, excellent agreement is observed between the pressure measured from the volume of ice VII, the luminescence gauge and the volume of Cu. Good reproducibility of the sample pressure response to a given voltage function driving the piezo-actuator is observed. The quantities ΔP and Δt defined in the text are represented for each run. Note the break in scale for the horizontal axis.

Full size image

As shown in Figs. 2 and 3, two quantities are defined for future data analysis: Δt, representing the duration over which fluid water remained in its metastable state along a given pressure ramp; ΔP, indicating the over-compression pressure, i.e., the pressure differential between crystallization and the associated ice VII melting at the same temperature.

Crystallization of ice VII in the stability domain of ice VI

Between compression rates of 0.15 GPa/ms and 0.9 GPa/ms, water remains metastable up to pressures ranging from 1.56 GPa and 2.1 GPa, respectively. This pressure range corresponds to the previous domain of investigation in d-DAC experiments focusing on the solidification of metastable water19,20,21. However, the findings from these studies appear contradictory. One study suggested the solidification into ice VII19, supported by a plateau around 1.5 GPa in the pressure response of the sample, similarly to that depicted in Fig. 2. Another study proposed that ice VII germinating in the stability field of ice VI evolves into amorphous HDA ice, based on the Raman measurements taken at the end of the compression20. In a third study, a mixture of ice VI and vitreous ice was observed by Raman and XRD measurements taken at the end of the pressure ramp21. The situation is puzzling and prompts the need for time resolved XRD measurement to elucidate the structure of the nucleated ice and the mechanism of its growth and transformation over time. Time resolved XRD measurements of metastable water crystallizing at 1.75 GPa are shown in Fig. 4. After azimuthal integration, the time resolved XRD data is represented as a 2D plot with diffraction angle on the x-axis, time on the y-axis and intensity displayed using a gray color scale. The XRD signal of ice VII (evidenced by the strong (110) peak) emerges first, followed by the appearance of the ice VI XRD pattern (evidenced by its 3 main peaks) after 200 μs, with its intensity increasing over time. After maintaining the sample at its peak pressure of 1.8 GPa for a few minutes, the integrated diffraction pattern (Fig. 4, top) indicates a mixture of ice VI and ice VII. The present observations support the hypothesis that metastable water, within the pressure range of 1.5 GPa to 2.1 GPa, nucleates into ice VII first, despite this range being the stability field of ice VI. Ice VI nucleation is also observed after a few hundred microseconds, revealing the difference in nucleation time between ice VI and ice VII. In this pressure domain, where both phases are stable, the faster nucleation of ice VII could be attributed to a similarity of the local order between the liquid and ice VII, resulting in a lower interfacial energy and thus a lower nucleation barrier, leading to earlier nucleation19. Here, the ice sample remaining as a mixture of ice VI and ice VII is observed at 1.8 GPa, as inferred from the measured volumes of Sn, ice VII and VI. In another XRD study, a mixture of ice VI and amorphous ice was reported at 1.7 GPa21. This difference could be explained by the fact that at 1.8 GPa, ice VII is approaching its thermodynamic stability, allowing for the stabilization of a mixture of ice VI and ice VII (and a possible amorphous state, which could not be observed in our case since its low scattering may be hidden in the Bragg peaks), whereas at 1.7 GPa, ice VII has been reported to gradually transform in a mixture of ice VI and amorphous ice. These results offer a clarification to the apparent contradiction of the previous findings.

Fig. 4: The time evolution of the integrated XRD image of water freezing under a 0.8 GPa/ms compression rate.
figure 4

Metastable water crystallizes first into ice VII as evidenced by the appearance of its (110) peak at 580 μs.  ~200 μs later, diffraction peaks attributed to ice VI are observed. The horizontal red and green lines mark the apparition of the ice VII and ice VI respectively. Top: integrated diffraction pattern of the same sample held at the maximum pressure of 1.8 GPa taken after a few minutes. A mixture of ice VI and ice VII is still observed.

Full size image

Freezing pressure of metastable water versus compression rate

The pressure limit of metastable water is here observed to continuously increase with the compression rate, by scanning the compression rate over 4 orders of magnitude in the d-DAC. Water can be over-compressed up to 2.9 GPa at 300 K for a compression rate of 110 GPa/ms. This value is much lower than the pressure limit of metastable water in ns-dynamic measurements7 which has been reaching 8 GPa for compression rate about 4 orders of magnitude higher than the one in d-DAC. Given that the compression ramp is isothermal in the d-DAC while it is isentropic in the ns-compression ramps, a consistent metric for the overpressure value is necessary. The differential pressure ΔP, as previously defined, is used. For the isentropic ramps, the measured pressure limit of metastable water, Plim, is converted into ΔP by computing the difference between Plim and the associated ice VII melting pressure at the temperature of the isentrope at Plim, as illustrated in the inset of Fig. 5. Figure 5 plots in a semi-logarithmic scale the metastability pressure limit of water as a function of compression rate, obtained here using the d-DAC and utilizing data from other various platforms7,16,17,18 (excluding the data of Gleason et al. due to heterogeneous nucleation15), so spanning six orders of compression rates. Remarkably, the various datasets align smoothly on an increasing trend. Recently, Myint et al. have proposed a scaling law for the onset of solidification at extreme over-compression of liquids8, with ΔP being a power function of the compression rate Π. We have fitted the dataset in Fig. 5 with a similar power function ΔP = aΠc + b. Notably, the exponent c of the fit equals to 0.056, which agrees with the one given by the Myint’s scaling law, equal to 0.069. The validity of such a scaling law is thus extended over the whole range of compression rates leading to freezing of metastable water into ice VII. It should be noted though that the constant b is added here to take into account the need of a minimal compression rate above which freezing of metastable water into ice VII is observed.

Fig. 5: Over-compression (ΔP) as a function of compression rate (Π).
figure 5

Our data points alongside the averaged points from refs. 7,16,17,18 are reported. Temperature at freezing is shown as a color-scale. The gray-dashed lines is the best fit result of the power function ΔP = aΠc + b, with a = 2.6654, b = −2.2544 and c = 0.0564. Inset: Low-pressure phase diagram of H2O showing how the ΔP is calculated for isentropic compressions of refs. 7,17. Errors bars are estimated from the pressure measurements and from the ones given in the literature.

Full size image

Over-pressurization is conceptually equivalent to isobaric cooling. When metastable water freezes under a compression rate of 110 GPa/ms, it corresponds to a cooling rate of 107 K/s. Such a rate has been utilized to observe the vitrification of water by spraying water in a cryogenic medium34. In contrast here, a solidification into ice VII through homogeneous nucleation is observed.

Discussion

During the freezing of metastable water, we observe homogeneous nucleation of ice VII which uniformly fills the entire sample chamber, across the range of the compression rates investigated here with the d-DAC. Consequently, we analyze the freezing kinetics using the classical Johnson–Mehl–Avrami–Kolmogorov (JMAK) theory. Within this framework, the freezing kinetics incorporates contributions from the nucleation rate (γ) and the growth velocity of the ice germs (v), which are the two dominant mechanisms to obtain the kinetic time scale of freezing (τF), as: \({\tau }_{F}\propto {(\gamma {v}^{3})}^{-1/4}\)35. In highly metastable states, the nucleation rate predominates over the growth rate, thereby controlling the freezing kinetics. That is evidenced by the absence of a plateau in the pressure-time evolution in the d-DAC for compression rates above a few GPa/ms. According to Classical Nucleation Theory (CNT), the nucleation rate is proportional to the probability of spontaneously overcoming a free energy barrier associated with the formation of a critical-nucleus ice crystallite, expressed in terms of Δg, the Gibbs free energy difference between the liquid and the solid. The nucleation time and hence the freezing time can be expressed as:

$${t}_{n}=\frac{\exp \left(\frac{B}{{\Delta g}^{2}}\right)}{A}$$
(1)

where A and B are parameters specific to the nucleation process36. Δg can be calculated from the equation of state of solid ice VII and that of liquid extrapolated in the metastable domain. We estimate the volume variation over the pressure range covered here assuming a constant bulk modulus (2), that is those of the liquid19 and the solid31 calculated at the melting pressure:

$$\frac{\partial V}{\partial P}\approx -K{V}_{0}\ \Rightarrow \ V(P)={V}_{0}-K{V}_{0}P$$
(2)

Δg is then straightforwardly estimated in terms of the over-compression ΔP of the liquid and of the liquid-solid volume difference ΔVl−s by:

$$\Delta g=\int\Delta {V}_{l-s}\,dP=a+\Delta {V}_{{0}_{l-s}}\,\Delta P-\frac{1}{2}\Delta {(K{V}_{0})}_{l-s}\,\Delta {P}^{2}$$
(3)

From which the freezing time can be related to ΔP through the relation:

$${{{\rm{log}}}}({t}_{n})\propto {{{\rm{log}}}}({t}_{{{{\rm{min}}}}})+\frac{b}{{\left(a+\Delta {V}_{{0}_{l-s}}\Delta P-\frac{1}{2}\Delta {(K{V}_{0})}_{l-s}\Delta {P}^{2}\right)}^{2}}$$
(4)

This phenomenological model serves as a fitting function to correlate the freezing time of metastable water to the metastable over-pressure. In the dynamical compression of water described above, the freezing nucleation time is intertwined with the duration of the over-compression, Δt, with the nucleation time being tn = αΔt. We assume that α remains constant across the different experimental data, from the d-DAC to the ns-isentropic compressions. The freezing time is plotted against the over-compression in Fig. 6, where the proposed fit form in Eq. (4) accurately reproduces the entire dataset.

Fig. 6: Logarithm of the nucleation time as a function of over-compression.
figure 6

The nucleation time is assumed as tn = αΔt, with α = 1 for the figure. Changing α only changes the constant of the fit. Our data points with averaged points from refs. 7,17 are fitted using the CNT-based phenomenological model given in Eq. (4) with the three free parameters equal to: log(tmin) = −11.39, a = 5380.17 and b = 2.453e8. Inset: Extrapolation of the CNT model at large over-compression showing an asymptotic limit at the picosecond-timescale. The error bars in pressure are shown while those in time are smaller than the symbol size. They are estimated from the pressure measurements and from the ones given in the literature.

Full size image

The extrapolation of the fit to larger over-compression is shown in the inset of Fig. 6, revealing an intriguing asymptotic behavior at high over-compression. Beyond a ΔP of 10 GPa, the predicted freezing time of water is only a few picoseconds. Although such experimental over-compression seems unfeasible, numerical simulations are seen to validate the asymptotic behavior. Numerically, the thermodynamic conditions of metastable water can be established in less than a ps, and a freezing time of 12 ps has been reported for an overcompression of water about 30 GPa37. With increasing compression rate, water tends to reach a higher over-compressed metastable state. It has been suggested, though, that there exists a pressure limit close to 11 GPa for observing metastable water7, beyond which freezing should occur via mechanisms such as spinodal decomposition or amorphization. In contrast, we do not propose a pressure limit for metastable water here but instead suggest a freezing time limit of a few ps.

It is assumed that the dynamic compression experiments from refs. 17,7 resulted in a crystalline sample of ice VII. This assumption is reinforced by the coherence observed between the current d-DAC dataset and the previously obtained nanosecond-isentropic compression data. However, a clear confirmation through time-resolved XRD under isentropic compression is warranted, possibly utilizing a free electron-laser X-ray diffraction measurement, as in ref. 15, but assuring the conditions of homogeneous nucleation. Finally, the present study illustrates the remarkable ability of using the d-DAC to vary dynamic phenomena over four orders of magnitude of compression rate on the same platform, while simultaneously enabling detailed measurements of property evolution through time-resolved visual observation and XRD measurements.

Methods

X-ray diffraction measurements

X-ray diffraction experiments were carried out at the ID09 beamline of the ESRF. Data were collected using a 19 keV X-ray pink beam (1.5% bandwidth) focused to a 30 μm (FWHM) round spot. A 100 μm pinhole a few centimeters away from the sample was used to remove any contribution from the tails of the beam and from air scattering. The beamline heat-load chopper was operated at its slowest rotation speed in order to obtain X-ray pulses up to 1.5 ms, time long enough to cover the dynamics of interest. Diffraction images were collected using a JUNGFRAU 1M detector. The detector, composed of 2 tiles with 500k pixels each, has a 75 μm pixel pitch and uses a 320 μm thick silicon sensor. The detector was horizontally offset with respect to the direct X-ray beam to avoid radiation damage. It was operated in storage cell (SC) mode, where a burst of up to 16 images can be collected quickly and stored on a local, in pixel, analog memory for a later read-out. The maximum achievable frame rate during the burst is 250 kHz, with 1.5 μs exposures; however, the timing is adaptable, allowing for the utilization of longer periods and exposures if needed. In this study, the exposure time was typically 7 μs. The detector was controlled by the beamline control software via a custom TANGO device. Beside the run themselves, detector control included dark frames collection routines, which were individual per storage cell and timing setup. The timing of the measurement was orchestrated by the beamline control hardware, which would, in sync with the heat-load chopper, open the millisecond shutter to let the 1.5 ms long X-ray pulse on the sample, trigger the detector burst and the dDAC piezo controller. Sample-detector distance (~170 mm), tilt, and rotation were calibrated using a reference Bi sample with DIOPTAS38. The two-dimensional images from the JUNGFRAU detector were corrected for offset and gain, and then radially integrated using DIOPTAS. Individual peaks of both water and the X-ray gauge were fitted with a PseudoVoigt function for the determination of the lattice parameters.

SrB4O7 : Sm2+ fluorescence measurements

SrB4O7 : Sm2+ fluorescence signal was collected in a back-scattering geometry by an iXon electron multiplying (EM) CCD coupled to a 1200 l/mm grating, allowing a spectral resolution of approximately 0.08 nm. The iXon EMCCD is used in Fast-Kinetics mode, allowing the recording of spectra with an acquisition time varying from 1 to 500 μs with a time interval of  ~8 μs between each spectrum. SrB4O7 : Sm2+ fluorescence excitation was performed using 10 mW of a 491 nm Cobolt laser. With nonradiative decay times for Sm2+ ions typically in the range of a few nanoseconds39, SrB4O7 : Sm2+ emerges as an ideal pressure gauge for time-resolved experiments with a microsecond-level time resolution.

d-DAC experiments

Dynamic compression experiments were performed using a LeToullec DAC, i.e., a modification of the membrane-DAC40 with a piston guided by four rods, in conjunction with the Piezosystem Jena HPST 1000/35-25/80 VS45. A waveform Tabor Electronics WW2074 and an Amplifier Piezosystem Jena RCV 1000/7 are used to deliver the current in the piezoactuator with a chosen profile. DACs were equipped with Boehler-Almax design diamond anvils with 300 μm culets. Stainless steel gaskets were used for all experiments, indented to 40 μm thickness with a 100 μm-diameter hole for the experimental chamber.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.