Introduction

Parity-time (PT) symmetry fundamentally exploits the fact that non-Hermitian operators can have real eigenvalues under the common action of parity and time-reversal1. The symmetry can be broken after passing a critical exceptional point2 by increasing the non-hermiticity level of the system, leading to complex conjugate eigenvalues. The concept of PT symmetry was introduced by Bender and Boettcher in 1998, and since then it has been actively investigated in different fields that provide a variety of new opportunities with novel functionalities3,4,5,6,7,8,9,10,11. In particular, a PT-symmetric system with balanced gain and loss has attracted lots of attention to enable stable single-frequency operation in optics12,13,14, microwave photonics15,16,17, electronics18, and other related fields. PT symmetry is broken in these systems for the specific mode experiencing the highest gain, while for the rest losses overcompensate their gains12,13,14,15,16,17,18. Thus, stable single-frequency oscillation can be achieved.

Essentially, PT-symmetric single-frequency systems are static PT-symmetric systems, meaning that their properties, such as frequency, gain and loss, are time-invariant. Frequency-scanning systems featuring time-varying frequency are also widely employed in various fields19. For instance, Fourier-domain mode-locked optoelectronic oscillators (FDML OEOs)20,21 in microwave photonics, as well as FDML lasers22,23 and distributed feedback lasers in optics are typical examples of frequency-scanning systems, which can produce frequency-modulated continuous-wave (FMCW) microwave or optical waveforms for applications such as radar24,25,26, lidar27,28, optical coherence tomography (OCT)29, sensing30 and THz generation31. In those applications, FMCW waveforms with narrow instantaneous linewidth are desired, since a wide instantaneous linewidth would deteriorate the resolution of radar and lidar systems32,33. However, there are generally multiple oscillation modes that occur simultaneously in the frequency-scanning process, due to the lack of an effective cavity mode selection mechanism. For example, bandpass filters are the most commonly used cavity mode selection tools in an FDML OEO. The typical 3-dB bandwidth of a bandpass filter is in the order of tens of MHz, which is much larger than the mode spacing (in the order of tens of kHz) of an FDML OEO. Thus, the instantaneous linewidth of a frequency-scanning system is large, limiting the performance for practical applications.

Here we introduce the PT symmetry concept to time-variant frequency-scanning systems. Time-variant PT symmetry equations and eigenfrequencies for the frequency-scanning systems are developed based on the coupled mode theory. We show that the instantaneous linewidth of the frequency-scanning systems can be narrowed dynamically by time-variant PT symmetry breaking. A time-variant PT-symmetric frequency-scanning FDML OEO is constructed as a test bed in a proof-of-concept experiment. It has a dual-loop structure, with one having a gain and the other having a loss of the same magnitude. The gain and loss coefficients are also precisely controlled to ensure that they are greater than the coupling coefficient for PT symmetry breaking. The instantaneous linewidth of the time-variant PT-symmetric FDML OEO is only 0.18 MHz, which is narrowed down by a factor of 14 compared with that of a conventional FDML OEO. The 3-dB bandwidth of the de-chirped signal of the produced FMCW waveform is also greatly reduced, demonstrating the effectiveness of time-variant PT symmetry for dynamic linewidth narrowing in frequency-scanning systems. Moreover, radar point target imaging is carried out, which shows that the PT-symmetric FDML OEO-based radar is superior in performance as compared with a conventional FDML OEO-based radar. This study provides new insights into the use of PT symmetry for mode control and selection of time-variant frequency-scanning systems, and has great potential in applications such as modern radar and lidar systems.

Results

Time-variant PT-symmetric frequency-scanning system

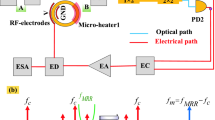
A comparison between a time-invariant PT-symmetric single-frequency system and a time-variant PT-symmetric frequency-scanning system is shown in Fig. 1a and b. Two coupled loops with balanced gain and loss are adopted for PT symmetry in both systems. Frequency-fixed filtering is employed in the PT-symmetric single-frequency system. While a frequency-scanning filter, whose passband frequency changes rapidly with time, is inserted into the PT-symmetric frequency-scanning system. Time-variant frequency-scanning operation, i.e., the generation of high-speed frequency-scanning signals, can therefore be enabled. To show the role of time-variant PT symmetry for frequency-scanning systems, the instantaneous gain-time diagrams of a conventional and PT-symmetric frequency-scanning system are illustrated in Fig. 1c and d, respectively. As can be seen, there are multiple modes that have positive net gain at the same time window for the conventional frequency-scanning system, which would oscillate simultaneously and result in a frequency-scanning signal with large instantaneous linewidth. When PT symmetry is broken in the time-variant system, the loss overcompensates the gain for all modes at the same time window, except the one with the highest gain, as we will prove theoretically in the next section. Thus, there is only one mode that has a positive net gain at a given time window, and the instantaneous linewidth of the frequency-scanning system can therefore be narrowed dynamically. Such a high-performance time-variant PT-symmetric frequency-scanning system can be used as a key signal source to provide the required narrow instantaneous linewidth FMCW waveform for different application scenarios, such as modern radar and lidar systems, as shown in Fig. 1e.

Fig. 1: Time-variant PT-symmetric frequency-scanning system.
figure 1

a Illustration of a time-invariant PT-symmetric single-frequency system (upper) and the produced single-frequency signal (lower). b Illustration of a time-variant PT-symmetric frequency-scanning system (upper) and the produced frequency-scanning signal (lower). c Instantaneous gain-time diagram (left) and net gain at a certain time window (right) for a conventional frequency-scanning system. a.u.: arbitrary units. d Instantaneous gain-time diagram (left) and net gain at a certain time window (right) for the PT-symmetric frequency-scanning system. e Example of the time-variant PT-symmetric frequency-scanning system in practical applications. It can be used as a key signal source to provide the required FMCW waveform for radar and lidar systems.

Full size image

Time-variant PT symmetry equations and eigenfrequencies for frequency-scanning systems

In contrast to a time-invariant PT-symmetric system with time-independent parameters, the key parameters, such as the instantaneous frequency, are varying with time for a time-variant PT-symmetric system. For a time-variant dual-loop frequency-scanning system, the signal amplitudes \({a}_{n}\) and \({b}_{n}\) of the two loops can be expressed in a form relating to the time dependence \(\exp (-i{\omega }_{{a}_{n}}t)\) and \({{{\rm{ex}}}}{{{\rm{p}}}}(-i{\omega }_{{b}_{n}}t)\), respectively, i.e.,

$${a}_{n}={A}_{n}\exp (-i{\omega }_{{a}_{n}}t)$$
(1a)
$${b}_{n}={B}_{n}\exp (-i{\omega }_{{b}_{n}}t)$$
(1b)

where \({A}_{n}\) and \({B}_{n}\) are the amplitude constants of the n-th order longitudinal mode, \({\omega }_{{a}_{n}}\) and \({\omega }_{{b}_{n}}\) are the instantaneous frequencies that change with time. The signal amplitudes \({a}_{n}\) and \({b}_{n}\) obey the following differential equations,

$$\frac{d{a}_{n}}{{dt}}=-i\left({\omega }_{{a}_{n}}+\frac{d{\omega }_{{a}_{n}}}{{dt}}t\right){A}_{n}\exp \left(-i{\omega }_{{a}_{n}}t\right)=-i\left({\omega }_{{a}_{n}}+\frac{d{\omega }_{{a}_{n}}}{{dt}}t\right){a}_{n}$$
(2a)
$$\frac{d{b}_{n}}{{dt}}=-i\left({\omega }_{{b}_{n}}+\frac{d{\omega }_{{b}_{n}}}{{dt}}t\right){B}_{n}{{{\rm{ex}}}}{{{\rm{p}}}}\left(-i{\omega }_{{b}_{n}}t\right)=-i\left({\omega }_{{b}_{n}}+\frac{d{\omega }_{{b}_{n}}}{{dt}}t\right){b}_{n}$$
(2b)

where \(\frac{d{\omega }_{{a}_{n}}}{{dt}}\) and \(\frac{d{\omega }_{{b}_{n}}}{{dt}}\) are the chirp rates of the two loops of the frequency-scanning system. Assuming the produced signal is a FMCW waveform and the two loops have the same instantaneous frequencies, we can have \({\omega }_{{a}_{n}}={\omega }_{{b}_{n}}={\omega }_{0}+kt\), where \({\omega }_{0}\) and \(k\) are the initial frequency and chirp rate of the FMCW waveform.

Assuming the coupling coefficient between the two loops is \({\kappa }_{n}\), the temporal evolution of the n-th order mode of the dual-loop frequency-scanning system can be described by a coupled differential equation12,34 that is related to \({\kappa }_{n}\) as well as gain and loss coefficients of the two loops

$$\frac{d{a}_{n}}{{dt}}=-i\left({\omega }_{{a}_{n}}+kt\right){a}_{n}+i{\kappa }_{n}{b}_{n}+{\gamma }_{{a}_{n}}{a}_{n}$$
(3a)
$$\frac{d{b}_{n}}{{dt}}=-i\left({\omega }_{{b}_{n}}+kt\right){b}_{n}+i{\kappa }_{n}{a}_{n}+{\gamma }_{{b}_{n}}{b}_{n}$$
(3b)

where \({\gamma }_{{a}_{n}}\) and \({\gamma }_{{b}_{n}}\) are the gain and loss coefficients of the gain and loss loops, respectively. Solving Eq. (3) (see Supplementary Note 1), we can get the eigenfrequencies \({\omega }_{n}^{({{\mathrm{1,2}}})}\) of the supermodes of the time-variant system, given by

$${\omega }_{n}^{(1,2)}={\omega }_{0}+{kt}+i\frac{{\gamma }_{{a}_{n}}+{\gamma }_{{b}_{n}}}{2}\pm \sqrt{{\kappa }_{n}^{2}-{(\frac{{\gamma }_{{a}_{n}}-{\gamma }_{{b}_{n}}}{2})}^{2}}\,$$
(4)

Assuming the exact PT condition can be satisfied, i.e., the gain and loss of the two loops are balanced: \({\gamma }_{{a}_{n}}=-{\gamma }_{{b}_{n}}={\gamma }_{n}\), the eigenfrequencies of the time-variant PT-symmetric system can be further simplified as:

$${\omega }_{n}^{(1,2)}={\omega }_{0}+kt\pm \sqrt{{\kappa }_{n}^{2}-{{\gamma }_{n}}^{2}}\,$$
(5)

Thus, similar to a PT-symmetric single-frequency system, there is also a transition point for the time-variant PT-symmetric frequency-scanning system when the gain/loss coefficient \({\gamma }_{n}\) is equal to the coupling coefficient \({\kappa }_{n}\). When the coupling coefficient \({\kappa }_{n}\) is greater than the gain/loss coefficient \({\gamma }_{n}\), each eigenfrequency is split into two frequencies. When the gain/loss coefficient \({\gamma }_{n}\) is larger than the coupling coefficient \({\kappa }_{n}\), \(\sqrt{{\kappa }_{n}^{2}-{{\gamma }_{n}}^{2}}\) becomes imaginary, and the PT symmetry is broken. At this condition, the amplitudes of the eigenmodes decay rapidly in the loss loop and increase rapidly in the gain loop. By precisely controlling the gain and loss of the two loops to ensure that PT symmetry is broken for modes in the frequency-scanning range, frequency-scanning oscillation with narrow instantaneous linewidth can be achieved.

Construction of a time-variant frequency-scanning oscillator

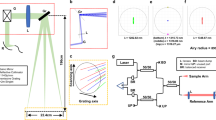
A time-variant PT-symmetric frequency-scanning FDML OEO is constructed as a testbed in an experiment. An FDML OEO20,35,36,37 in which a frequency-scanning bandpass filter is employed is an attractive microwave photonic system to study time-variant PT symmetry for producing a frequency-scanning signal. The frequency-scanning filter is incorporated into the FDML OEO cavity, whose scanning period is synchronized with the time delay of the OEO cavity to enable Fourier domain mode locking20,22. Fig. 2a illustrates the structure of the time-variant PT-symmetric FDML OEO. A light source is used to produce a wavelength-swept optical light, which is launched into a phase modulator (PM) for electrical to optical modulation. A phase-modulated light is generated which is then coupled to an optical notch filter for phase-modulation to intensity-modulation conversion38,39 by filtering out one of the phase-modulated sidebands. An electrical signal is then generated at the output of a photodetector (PD). The joint operation of the light source, the PM, the optical notch filter, and the PD corresponds to a frequency-scanning microwave photonic filter (MPF)20. The instantaneous frequency of the FDML OEO is changing with time due to the utilization of the frequency-scanning MPF, thus the FDML OEO can be used as a testbed for time-variant PT symmetry in frequency-scanning systems. A frequency-fixed filter was adopted in previous PT-symmetric systems15,16, which feature a time-independent frequency and are suitable for the study of time-invariant PT symmetry. To achieve time-variant PT symmetry, a dual-loop structure with the two loops mutually coupled is adopted in Fig. 2a. As can be seen in Fig. 2a, the phase-modulated light is divided into two paths using an optical coupler (OC) with each path having a tunable delay line (TDL), a tunable optical attenuator (TOA) and a PD. Two microwave signals are generated at the outputs of the PDs and they are combined by using an electrical coupler (EC1). Note that the two TOAs are used to control the gain and loss of the two loops and the two TODLs are employed to ensure the two loops have an equal delay time. When the time-variant PT symmetry is broken, i.e., the gain/loss coefficients are larger than the coupling coefficient of the two loops, the instantaneous linewidth of the produced FMCW waveform can be narrowed. Optoelectronic devices such as the PD and electrical amplifier generally have frequency-dependent responses, which may lead to different gain and loss for different modes of the FMCW waveform. In our experiment, we carefully selected optoelectronic devices with flat frequency responses to ensure that the gain and loss are well balanced for different modes. Customized equalizers can also be incorporated into the OEO loop to compensate for the frequency-dependent responses of the loop devices, therefore ensuring a flat gain and loss for different modes.

Fig. 2: Produced FMCW waveform with narrow instantaneous linewidth.
figure 2

a Block diagram of a PT-symmetric frequency-scanning FDML OEO that used in the experiment. SLS: Swept light source; PM: phase modulator; EDFA: Erbium-doped fiber amplifier; OC: optical coupler; TOA: tunable optical attenuator; TDL: tunable delay line; PD: photodetector; EC: electrical coupler; EA: electrical amplifier. b Temporal waveform of the generated FMCW waveform. c Instantaneous frequency-time diagram calculated by the short-time Fourier transform of the temporal waveform. d Instantaneous frequency-time diagram obtained based on self-homodyne and the Hilbert transformation. Inset: Zoom-in view showing the instantaneous linewidth of the time-variant PT-symmetric frequency-scanning oscillator. e Instantaneous frequency-time diagram of a FMCW waveform generated by a conventional frequency-scanning oscillator. Inset: Zoom-in view showing the instantaneous linewidth. f Frequency error between an FMCW waveform generated by the time-variant PT-symmetric frequency-scanning oscillator and an ideal linear FMCW waveform. g Frequency error between an FMCW waveform generated by a conventional frequency-scanning oscillator and an ideal linear FMCW waveform.

Full size image

Produced FMCW waveform with narrow instantaneous linewidth

In the experiment, the two TODLs are first precisely tuned to ensure that the two loops have an identical loop delay. The total loop delay of the ring cavity is \({T}_{{{{\rm{loop}}}}}=\)15.77 \({{{\rm{\mu }}}}{{{\rm{s}}}}\), corresponding to a free spectral range (FSR) of 63.4 kHz. The oscillation gain and the loss of the two loops are then controlled by adjusting the TOAs to achieve PT symmetry. The optical powers at the inputs of the two PDs are measured to be \({P}_{g0}=-7.19{{{\rm{dBm}}}}\) and \({P}_{\gamma 0}=-7.50{{{\rm{dBm}}}}\) for the gain and loss loops, respectively, such that the OEO starts to oscillate. Thus, the optical power \({P}_{g}\) of the gain loop and \({P}_{\gamma }\) of the loss loop are adjusted to satisfy \({P}_{g}-{P}_{g0}={P}_{\gamma 0}-{P}_{\gamma }\) to meet the PT symmetry condition. Finally, the EDFA and TOAs are precisely tuned to ensure that the gain/loss coefficient is larger than the coupling coefficient of the two loops, thus the PT symmetry is broken and the time-variant PT-symmetric FDML OEO produces a narrow instantaneous linewidth FMCW waveform.

The measured temporal waveform and calculated instantaneous frequency-time diagram using the short-time Fourier transform (STFT) of the produced FMCW waveform are shown in Fig. 2b and c, respectively. Clearly, the produced signal is a linear FMCW waveform with good linearity. However, it is difficult to evaluate the instantaneous linewidth directly using the result in Fig. 2c due to the tradeoff between the time and frequency resolution of the STFT process40. By using self-homodyne and the Hilbert transformation (HT)41,42, the instantaneous frequency of the FMCW waveform is calculated with high resolution and shown in Fig. 2d. An equivalent 16-m long MZI delay line is used in the self-homodyne process, and a short delay line is suitable for measuring the instantaneous frequency using the HT algorithm42. The instantaneous frequency of an FMCW waveform generated by a conventional frequency scanning FDML OEO without PT symmetry is also shown in Fig. 2e for comparison. The result in Fig. 2e is obtained by disconnecting the loss loop in Fig. 2a, so that the PT-symmetric frequency-scanning FDML OEO degenerates into a conventional OEO while maintaining the same system parameters. The region of interest (ROI) is 90% in Fig. 2d and e. As can be seen from the zoom-in view of the two instantaneous frequency-time diagrams, the instantaneous linewidth of the FMCW waveform generated by the time-variant PT-symmetric frequency-scanning oscillator is only 0.18 MHz, which is narrowed by a factor of 14 compared with that generated by the conventional frequency-scanning oscillator. Periodic fluctuation can also be observed in the zoom-in view of the instantaneous frequency-time diagram of the conventional frequency-scanning oscillator in Fig. 2e, which could be related to the mode competition effect since there are multiple modes that have net gains greater than unity. These modes would compete once the FDML OEO is switched on, and periodic fluctuation may be obtained as a result of the competition between the different modes. The frequency errors of the FMCW waveforms generated by the two oscillators compared with an ideal linear FMCW waveform are shown in Fig. 2f and g. A significant reduction in the frequency errors of the time-variant PT-symmetric frequency-scanning oscillator can be observed. The frequency error in Fig. 2f could be related to the nonlinearity in the frequency scanning process, which can be further reduced by using frequency scanning linearization methods42,43. In addition, the frequency error could also be related to the noise of the optoelectronic devices in the time-variant PT-symmetric FDML OEO loop. The linearity of the PT-symmetric frequency-scanning oscillator is also much better than that of the conventional frequency-scanning oscillator. Metrics such as the root mean square \({v}_{{{{\rm{rms}}}}}\) of the residual nonlinearity and the linear regression coefficient of determination \({R}^{2}\) can be used to describe the linearity of the produced FMCW signal42. \({v}_{{{{\rm{rms}}}}}\) and \(1-{R}^{2}\) of the FMCW signal generated by the time-variant PT-symmetric frequency-scanning FDML OEO are calculated to be 0.7 MHz and \(7.7\times {10}^{-6}\), respectively, which are significantly reduced (i.e. by two orders of magnitude) compared with that of the FMCW signal without PT symmetry (\({v}_{{{{\rm{rms}}}}}=7.5\,{{{\rm{MHz}}}}\) and \(1-{R}^{2}=7.1\times {10}^{-4}\), see Supplementary Note 4 for further information). This again demonstrates the powerful mode control and selection property of the time-variant PT symmetry for a frequency-scanning system. The instantaneous linewidths have also been narrowed by a factor of more than 10 for different modulation frequencies (see Supplementary Note 6), and the frequency noise of the PT-symmetric oscillator can also be reduced compared with that of a conventional oscillator (see Supplementary Note 7). The scanning bandwidth is also an important parameter for practical applications such as a FMCW radar. The scanning bandwidth of the proposed scheme is determined by the frequency responses of the optoelectronic devices in the FDML OEO loop, including the frequency responses of the PM, the optical notch filter, the PD, and the electrical amplifier. Since optoelectronic devices with a wide frequency range of tens of GHz are commercially available, the scanning bandwidth could reach tens of GHz. At the same time, the optoelectronic devices should be carefully selected to ensure that they have flat frequency responses, since the gain and loss for different modes in the scanning range should be balanced to achieve PT symmetry in the proposed scheme.

De-chirping of the produced FMCW waveform

We also measured the de-chirped signal of the FMCW waveform produced by the time-variant PT-symmetric and conventional FDML OEO. The de-chirped signal is obtained by beating an echo signal with the transmitted FMCW waveform, which is widely used in radar and lidar systems32,33. By measuring the frequency of the de-chirped signal, the range of a target can be obtained. To improve the range resolution, an FMCW waveform with a high linearity and narrow instantaneous linewidth is desired since the width of the de-chirped signal mainly depends on the nonlinearity and the instantaneous linewidth of the FMCW waveform. The schematic diagram of the de-chirp processing is shown in Fig. 3a, where the echo signal with a time delay of \(\triangle t\) is mixed with the transmitted FMCW waveform through an electrical mixer. A de-chirped signal that is related to the nonlinearity and instantaneous linewidth of the FMCW waveform is therefore obtained, as shown in Fig. 3b and c. The spectra of the de-chirped signals generated by using an FMCW waveform of the time-variant PT-symmetric frequency-scanning oscillator and that of a conventional frequency-scanning oscillator are shown in Fig. 3d and e. The FMCW waveform of the conventional FDML OEO for de-chirping is obtained when the PT-symmetric FDML OEO is degenerated into a conventional one while maintaining the same system parameters. Therefore, the difference between the two de-chirped signals also shows the value of time-variant PT symmetry for frequency-scanning systems. As can be seen from Fig. 3d and e, the de-chirped signal corresponding to the time-variant PT-symmetric frequency-scanning oscillator has a narrower 3-dB bandwidth of about 53 kHz, while the de-chirped signal corresponding to the conventional frequency-scanning oscillator has a much wider 3-dB bandwidth as large as 1.2 MHz. The difference between the two de-chirped signals is mainly due to the differences in the initial linearity and instantaneous linewidth of the two FMCW waveforms, which are caused by the introduction of time-variant PT symmetry in the frequency-scanning system. The 23-fold reduction in the 3-dB bandwidth of the de-chirped signal reflects the effective dynamic linewidth narrowing capability of employing time-variant PT symmetry in a frequency-scanning system. Moreover, we also measured the details of the two de-chirped signals under a higher resolution bandwidth. The results are shown in Fig. 3f and g, which allow us to see more details about the spectra of the de-chirped signals. Specifically, Fig. 3f contains details within and outside the 3-dB bandwidth of the de-chirped signal of the time-variant PT-symmetric frequency-scanning oscillator, while Fig. 3g only includes details within the 3-dB bandwidth of the de-chirped signal of the conventional frequency-scanning oscillator due to the relatively large 3-dB bandwidth of its de-chirped signal. The side-mode suppression ratio of the de-chirped signal corresponding to the time-variant PT-symmetric frequency-scanning oscillator reaches 30.1 dB, while the de-chirped signal corresponding to the conventional frequency-scanning oscillator has multiple peaks. This again demonstrates the benefits of employing time-variant PT symmetry in a frequency-scanning system.

Fig. 3: De-chirped signal using the FMCW waveform generated by the time-variant PT-symmetric and conventional FDML OEO.
figure 3

a Schematic diagram of the de-chirp processing link. Illustrations of the instantaneous frequency-time diagram and de-chirped signal of b the time-variant PT-symmetric FDML OEO and c a conventional FDML OEO. Spectra of the de-chirped signal of d the time-variant PT-symmetric FDML OEO and e a conventional FDML OEO. Insert: Zoom-in view showing the 3-dB bandwidth of the de-chirped signal. Details of the de-chirped signal corresponding to f the time-variant PT-symmetric FDML OEO and g a conventional FDML OEO. RBW: resolution bandwidth.

Full size image

Radar point target imaging using the PT-symmetric frequency-scanning system

To further investigate the impact of using an FMCW waveform with a reduced instantaneous linewidth on the performance for practical applications, radar point target imaging using an FMCW waveform is investigated. The point target imaging results are acquired by inverse synthetic aperture radar (ISAR) imaging44, and the results are shown in Fig. 4. The radar range profiles obtained by matched filtering are also given in Fig. 4. We can see that the peak-to-side lobe ratio of the range profile based on the time-variant PT-symmetric FDML OEO is more than 41 dB, which is 11-dB higher than that of the range profile based on the conventional FDML OEO. The two targets are also more distinguishable in the range direction in the two-dimensional point target imaging result based on the time-variant PT-symmetric FDML OEO, due to the reduced instantaneous linewidth of the FMCW waveform. Thus, the performance for practical applications can be enhanced by utilizing PT symmetry for linewidth narrowing in frequency-scanning systems. It should be noted that the imaging quality is similar in the azimuth direction in the point target imaging results based on oscillators with and without PT symmetry. The reason is that the resolution of the azimuth direction is determined by the length of the synthetic aperture of the radar44, which is the same for the two systems. The target recognition in Fig. 4d is better than that of Fig. 3g, although the same FMCW waveform is used. The difference in target recognition is due to the use of two different signal processing methods. Figure 3g is obtained by de-chirp processing, where multi peaks can be observed due to the relatively poor signal quality of the FMCW waveform of the conventional FDML OEO. Figure 4d is acquired by ISAR imaging, where the target can be recognized and the relatively poor signal quality of the FMCW waveform of the conventional FDML OEO is reflected by the high sidelobes in the range direction.

Fig. 4: Radar range profiles and point target imaging results.
figure 4

The results of radar range profiles based on a the time-variant PT-symmetric and b conventional frequency-scanning oscillators, and the point-target imaging results based on c the time-variant PT-symmetric and d conventional frequency-scanning oscillators.

Full size image

Discussion

In addition to the time-variant PT-symmetric frequency-scanning system that is studied in this paper, PT symmetry has also been explored in systems with time-dependent gain/loss or coupling coefficient45,46,47, which also provides an interesting perspective for the study of PT symmetry in time-variant systems. We would like to clarify, however, this is the first time to study PT symmetry in time-variant frequency-scanning systems to the best of our knowledge, which we believe is suitable not only for the frequency-scanning FDML OEO that has been demonstrated in our experiment but also for other types of frequency-scanning systems such as frequency-scanning lasers and frequency-scanning electrical signal generators, which are highly desirable in applications such as radar, lidar, OCT, sensing and THz generation.

In conclusion, we have investigated the time-variant PT symmetry in frequency-scanning systems. We showed that the instantaneous linewidth of a frequency-scanning system can be dynamically narrowed down when PT symmetry is broken for eigenmodes in the frequency-scanning range. A time-variant PT-symmetric frequency-scanning FDML OEO was constructed as a testbed in our experiment. The instantaneous linewidth of the produced FMCW waveform was narrowed by a factor of 14 compared with that of a conventional frequency-scanning oscillator. The 3-dB bandwidth of a de-chirped signal resulting from the FMCW waveform generated by a PT-symmetric frequency-scanning FDML OEO was also reduced compared with that generated by a conventional frequency-scanning oscillator. Moreover, point target imaging results indicated that the time-variant PT-symmetric FDML OEO-based radar system outperforms a conventional FDML OEO-based radar system. Our study provides new insights into the use of time-variant PT symmetry for mode control and selection of frequency-scanning systems and shows great promise in applications including radar and lidar systems.

Methods

Configuration

The time-variant PT-symmetric frequency-scanning oscillator in Fig. 2a was constructed using commercially available optoelectronic devices. The SLS consists of a single frequency laser, a dual parallel Mach-Zehnder modulator (DPMZM), and an optical bandpass filter (OBPF) (see Supplementary Note 2). The single frequency laser (Agilent 8164B) emits an optical carrier signal with a wavelength of 1550.442 nm and an output power of 4.26 mW. The optical carrier is modulated by a swept microwave signal at the DPMZM (IXblue MXAN-LN-40) to produce swept optical sidebands. The OBPF (YENISTA OPTICS XTA-50) out one of the first-order sidebands, thus a swept optical signal is obtained. The bandwidth of the PM is about 40 GHz. The optical notch filter has a 3-dB bandwidth of 50 MHz. The length of the optical fiber used in the experiment is 3.1 km. The two TODLs have a tuning range of 8 cm and a tuning resolution of 0.05 mm. The PDs (Agilent 11982 A) have a 3-dB bandwidth of 15 GHz. The output of the low-noise amplifier (SHF S126 A) is connected to the radio frequency (RF) input of the PM to form a closed FDML OEO loop.