On the structure of species-function participation in multilayer ecological networks

Abstract

Understanding how biotic interactions shape ecosystems and impact their functioning, resilience and biodiversity has been a sustained research priority in ecology. Yet, traditional assessments of ecological complexity typically focus on species-species interactions that mediate a particular function (e.g., pollination), overlooking both the synergistic effect that multiple functions might develop as well as the resulting species-function participation patterns that emerge in ecosystems that harbor multiple ecological functions. Here we propose a mathematical framework that integrates various types of biotic interactions observed between different species. Its application to recently collected data of an islet ecosystem—reporting 1537 interactions between 691 plants, animals and fungi across six different functions (pollination, herbivory, seed dispersal, decomposition, nutrient uptake, and fungal pathogenicity)—unveils a non-random, nested structure in the way plant species participate across different functions. The framework further allows us to identify a ranking of species and functions, where woody shrubs and fungal decomposition emerge as keystone actors whose removal have a larger-than-random effect on secondary extinctions. The dual insight—from species and functional perspectives—offered by the framework opens the door to a richer quantification of ecosystem complexity and to better calibrate the influence of multifunctionality on ecosystem functioning and biodiversity.

Introduction

All ecosystems are composed of species participating in a myriad of entangled interactions with other co-existing species^1,2,3. These interactions involve the many different ecological roles that species perform, which define the multiple dimensions of their Eltonian niche^4,5. To better understand the rich phenomenology^6,7 of these interactions, species⁸, and their interaction diversity⁹ can be quantified by the degree to which species participate in different ecological functions^10,11 (e.g., pollination, seed dispersal, nutrient uptake, decomposition, etc.).

A standard modeling approach to describe ecosystem functioning places coexisting species at the center, and thus represents it as an entangled web of species interacting via a concrete interaction type (e.g., food webs^{12,13,14,15,16}, mutualistic networks^{3,17,18,19,20}, etc.). Network science^18,21 has been instrumental in this approach, providing quantitative insights on e.g., the emergence of species extinction cascades^18,21,22, or the impact of network structure on biodiversity^13,23,24, among others^17,25. While not always strictly necessary^26,27, incorporating more than one type of interaction between species into a single model often suggests using multilayer network theory^28,29,30,31, i.e., where different species-species networks (one per interaction type) can be represented, what would, in principle, enable us to understand e.g., how multifunctionality impacts ecosystem’s biodiversity^{13,14,23,32,33,34,35}, among other important ecological questions^17,25. However, and despite some notable examples^36,37, embracing multilayer network theory in ecology faces at least three challenges that have precluded substantial advances to date: first, from an experimental angle, accessing the necessary fine-grained empirical observations of species interactions is inherently a difficult task³⁸, often resulting in incomplete observations or indirectly-inferred data^39,40. Second, interactions that explicitly contribute to different ecological functions are usually measured with different methods, and thus their estimated strength has often different units. For example, it is not straightforward to compare e.g., how a flowering plant being visited by three pollinators is comparable to a plant being eaten by three herbivores (see ref. ⁴¹ for a recent effort to address this challenge through the use of energy fluxes). Third, the proper quantification of ecologically relevant properties in terms of multilayer network metrics is still in its infancy. All in all, integrating several ecological functions into a single modeling framework—both theoretically and empirically—thus represents both a necessity and a challenge⁴². We call this Challenge 1, and it constitutes the first motivation of this paper.

Interestingly, ecosystem’s functioning could be probed from other perspectives as well, not only a species-centric one. As advanced at the beginning, one could focus on how entangled species and functions are—i.e., how different species participate in interactions cataloged as different ecological functions–, resulting in “species-function” networks. Such representation would allow to quantify the importance that different (i) species and (ii) functions have. Analysis of point (i) inquires whether there are species that are disproportionally participating and connecting more functions. This would enrich the polyhedric concept of keystone species^{43,44,45,46,47}—traditionally defined as those species disproportionately important for community functioning, regardless of their abundance—but considering here the concomitant participation of species in different functions⁴⁸—and their role in connecting them—as the measures under analysis. Analysis of (ii) would inform a similar analysis but conceived here in the context of functions rather than species, inquiring whether, even if all ecological functions are important, their roles and impact as ecosystem connectors are similar or not, and whether there exists a core of ecological functions that play a salient role. This species-function perspective opens up further questions: first, the ecosystem could be modeled as an entangled web of functions^49,50 (e.g., herbivory interfering pollination, feedback loops between pollination and seed dispersal, etc.), effectively resulting in function-function networks where links between two functions are based on, e.g., whether there are species that participate in both functions. Understanding how ecological functions relate to one another within a single ecosystem would provide a functional perspective of important questions, such as the role of indirect effects, or the ecosystem’s resilience against function perturbations⁵¹. Second, a similar question could be raised now from the species-centric viewpoint, inquiring how species would relate to each other based on the functions they share. In a nutshell, ecosystems are inherently multidimensional complex systems, and inspection of different properties require representing the ecosystem in different ways. Leveraging multilayer network theory to implement the species-function perspective described above, along with the outlined analysis, constitutes what we call Challenge 2 and is the second motivation of this paper.

Here we take steps to address Challenges 1 and 2 discussed above, both theoretically and empirically. On the theoretical side, expanding from multilayer network theory, we develop a modeling approach inspired by the consumer-resource paradigm^19,52, whereby plant species are seen as “resources”, and “consumers” encapsulate different taxa of animals or fungi involved in both mutualistic and antagonistic interactions. These biotic interactions can be of different types and, following Garland and co-authors¹⁰, are cataloged into different ecological functions. Indeed, functions are defined here as interaction types with specific ecological repercussions, see Methods for details. On the experimental side, we leverage the relative simplicity of a small island community —Na Redona, in the Balearic Islands (Western Mediterranean Sea)—to test our methodological framework. We develop methods to standardize field-sampling in Na Redona, resulting in a database encompassing a total of 1537 weighted interactions between plants, animals and fungi across six ecological functions that, for the purpose of this work, we categorize as pollination, herbivory, seed dispersal, decomposition, nutrient uptake, and fungal pathogenicity (see Methods) and then apply our theoretical framework to unveil the multifunctional architecture of this ecological community and its impact in various ecologically-relevant properties.

Operationally, our modeling framework starts by recasting our whole dataset into a resource-consumer-function (RCF) tensor—a generalization of a matrix with three indices instead of two, hereafter RCF tensor—that we define below (see Fig. 1 for the work’s roadmap and Table 1 for a glossary of the concepts introduced herein). By suitably interpreting the indices of this tensor as nodes or layers respectively, the RCF can then be visualized as a multilayer (multifunctional) weighted network. Subsequently, by mathematically integrating out the consumer index in the RCF tensor, we obtain a resource-function matrix (effectively, a bipartite species-function network) that encodes how plant species and functions participate one onto each other within the ecosystem. We show that, applied to the Na Redona community, such resource-function matrix displays statistically significant nested pattern⁵³, providing evidence that both species and functions play heterogeneous and dual roles and participate into each other in a non-random way. This also opens the possibility of quantifying and ranking the “importance” of both species and functions accordingly. Among many possibilities, here we do this (i) by computing a score-based on the direct connections in the bipartite species-function network and another score-based on how species indirectly connect functions and viceversa, (ii) by certifying that the resulting rankings are in good agreement with each other, and (iii) by checking which positions in these rankings are statistically significant according to suitable null models. Also, since a connection or a path is not necessarily an effect⁴⁴, we perform an extinction analysis and confirm that removing species and functions in the order predicated by these rankings has a larger-than-random effect on secondary extinctions in the system. Application to the Na Redona dataset unveils a hierarchical pattern and allows us to indentify a small subset of (multifunctional) “hub” plant species and a single “hub” function. We further show that these actors play an important role in the assembly of the species-function participation pattern, as the removal of these species and functions have a larger effect in the subsequent extinction of species/functions than expected, hence calling them “keystone”. We end up by discussing these results, their ecological implications and outlining a number of concluding remarks.

Fig. 1: Conceptual framework.

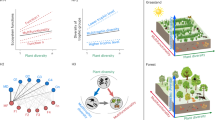
(see also Table 1 for a glossary of terms). Ecosystems are multidimensional complex systems whose interactions are captured by a rank-3 resource-consumer-function (RCF) tensor (here, a plant-animal/fungus ecological interaction tensor) with entries ${f}_{ix}^{\alpha }$. This tensor can be visualized as a multilayer (multifunctional) ecological network (see Fig. 2) when identifying the indices i and x with resource and consumer nodes, respectively, and index α with ecological function layers. Integrating consumers out (see Eq. (1) in the text and Methods), we obtain a resource-function matrix P (Fig. 3) that encapsulates how plant species and functions are intertwined in the ecosystem. Further projections of this matrix yield function-function networks Φ (Fig. 4) that characterize how each plant species connects different functions (phytocentric embedding) and plant-plant networks Π (Fig. 5) that characterize how each ecological function connect different plant species (function-centric embedding). Inspection of these networks allows us to rank species and functions based on how they participate and connect within the ecosystem. Created in BioRender⁹⁹.

Table 1 Glossary of terms and concepts sequentially introduced throughout the text, along with a short explanation

Results

Building the RCF tensor

Ecosystems are inherently multidimensional. From a modeling point of view, the precise span of such dimensions is necessarily driven by the extent of our data (see Methods), which includes direct observation of 16 plant species, 629 fungal ASV (i.e., amplicon sequence variants) and 46 animal species, whose interactions have been assigned to one of six functions: pollination, herbivory, seed dispersal, fungal decomposition, (fungal) nutrient uptake, or fungal pathogenicity (see Methods). Our complete dataset thus depicts the annotated co-occurrence of three features: resources (plant species) i interacting with (animal or fungal taxa) consumers x via an interaction type labeled as a function α. Mainly for notational convenience, this dataset is thus suitably formalized in terms of a rank-3 tensor ${{{\mathcal{F}}}}=\{{f}_{ix}^{\alpha }\}$ that we call the RCF tensor, where element ${f}_{ix}^{\alpha }$ specifies the observed probability of co-occurrence of such event. For the purpose of this work, note that a tensor is just a generalization of a matrix (matrices are particular types of rank-2 tensors), and allows us to encapsulate—and further manipulate- in a precise mathematical form our complete dataset (the need to employ tensors instead of matrices for notation stems from the fact that we have three concomitant indices, instead of two). Tensors have covariant and contravariant indices (e.g., a matrix has usually two covariant indices). In this work, we let resources i and consumers x be the covariant indices and α the contravariant one. All three i, x, α are running indices (e.g., α in ${f}_{ix}^{\alpha }$ should not be confused with a power). No sophisticated tensor algebra background is needed in this work, but for generic tensorial notation of multilayer networks, see ref. ²⁸.

In phytocentrically observed ecological functions, ${f}_{ix}^{\alpha }$ is then estimated from the proportion of all sampled plant species i that were observed to have interacted via α with consumer x (in every case we have $0\le {f}_{ix}^{\alpha }\le 1$, see Methods for details and explanations of how ${f}_{ix}^{\alpha }$ is built from the empirical observations). As a matter of fact, instead of ${f}_{ix}^{\alpha }$ one could have simply used the raw number of observed events (i.e., number of visits of a pollinator species to a plant species), but this would have prevented us to easily compare across events, e.g., how 5 visits of pollinators compare with 10 roots with fungi is cumbersome. This ambiguity fades away when employing probabilities of events.

Note that the tensorial formulation is not new, see ref. ²⁸. Here, all interactions are associated to a concrete function—i.e., a concrete layer, as we will show below–, and thus we only need three indices (hence a rank-3 tensor), not four as in the more general tensorial notation of multilayer networks²⁸. The analysis presented in what follows is based on simple manipulations (and their ecological interpretation) of the RCF, applications of these to the Na Redona case, and comparison of the results with respect to suitably defined null models.

RCF visualization: multilayer ecological network

Rank-3 tensors allow many possible visualizations, depending on specific interpretations of their running indices (see for instance Fig. 1 with the classical cube-like visualization). In our case, a natural and illuminating choice is to interpret two out of the three running indices as integer labels characterizing two groups of nodes of a (bipartite) network: plant species resources (index i = 1, …, 16) and animal/fungal consumers (index x = 1, …, 675). For a specific function α, ${f}_{ix}^{\alpha }$ simply denotes the (normalized) weight of the link between nodes i and x. Accordingly, each labeled ecological function α = 1, …, 6 corresponds to a different layer of the network, and thus by construction the resulting network is a multilayer one^28,29. It should be clear that this is just a concrete visualization of the RCF that allows us to properly interpret our ecological data. In this choice, each layer α summarizes the observed wiring architecture of the resource-consumer interactions conditioned on that particular function α. Of course, other choices are possible: one could for instance use the resource index i as the one identifying each layer, and thus under that choice the resulting multilayer network would visualize for each plant species layer how consumers participate in different functions.

Finally, one can also visualize a multilayer network in several ways. For illustration purposes, here we flatten layers by color-coding edges of the same layer, and in Fig. 2 we show the (edge-colored) network resulting from our Na Redona dataset (after having processed the layout via the Infomap community detection algorithm; details provided in Methods). This visualization reveals that consumers are often centered around a single plant species, forming clusters (see, however, the cluster consisting of Lavatera maritima and Geranium molle). Interestingly, cross-cluster links are also present, depicting that the ecosystem is formed by many clusters connected via an animal/fungus consortium. For alternative visualizations of the RCF tensor, see Supplementary Fig. 1.

Fig. 2: Multilayer Ecological Network visualization of the RCF tensor for the Na Redona dataset.

This is a basic visualization of our empirical RCF tensor, with 691 nodes (16 plant species and 675 animal/fungus taxa) interacting via six functions: pollination, herbivory, seed dispersal, decomposition of plant matter, nutrient uptake (mycorrhizas), and fungal pathogenicity, for a total of 1537 annotated interactions. Node colors account for plant species (green) and animal/fungus taxa (color-coded according to the primary function they are involved in). The sizes of plant nodes represent their observed abundance in the field (see Methods). Link widths quantify the estimated interaction probability. In this particular layout, by color-coding links according to their function (i.e., the layer), the multilayer network can be easily flattened and visualized. For readability, species are clustered via Infomap’s community detection algorithm (for other layouts and visualizations of the RCF tensor, see Supplementary Fig. 1). Infomap layout shows clusters of plant species surrounded by their consumer nodes, with various inter-cluster links.

Nestedness in the resource-function matrix

In this work, we are particularly interested in the role played by both plant species (resources) and functions, as well as how they are intertwined in the whole ecosystem, see Challenge 2 in the Introduction. To quantify such relationship, we start by “integrating out” the consumer indices of the RCF tensor to estimate the participation probability ${P}_{i}^{\alpha }$ of a given resource i in a given ecological function α. We define ${P}_{i}^{\alpha }$, under a no-correlation assumption, as the probability that resource i participates in function α (via the interaction with any potential consumer x). This is extracted from RCF through the expression

$${P}_{i}^{\alpha }=1-{\prod}_{x}\left(1-{f}_{ix}^{\alpha }\right).$$

(1)

See Methods for full details on the interpretation and derivation of Eq. (1), and why ${P}_{i}^{\alpha }$ is indeed a probability. Observe that this choice for computing ${P}_{i}^{\alpha }$ is parsimonious and can be refined to incorporate correlations (e.g., via the co-visitation patterns of two or more pollinator species) if empirical evidence of such correlation kernels is eventually available (e.g., via phylogenetic or trait similarity).

Accordingly, we can then build the resource-function matrix (rank-2 tensor) ${{{\bf{P}}}}=\{{P}_{i}^{\alpha }\}$. Using again a network perspective, P can be interpreted as the weighted biadjacency matrix of a bipartite resource-function network that links plant species and functions according to how likely these are related via their interaction with consumers, i.e., how likely plant species participate in functions and the other way around.

It should be stressed again at this point that the fact that both ${f}_{ix}^{\alpha }$ and ${P}_{i}^{\alpha }$ are probabilities of observing certain events as opposed to, say, a raw number of observations (number of visitations of pollinators, number of fungi found in the plant species, etc.) is not accidental. Much on the contrary, this is crucial to subsequently be able to make fair comparisons across functions (thereby reducing the problems that come from observational biases). It is indeed not always straightforward to compare a given plant species being pollinated by two animals vs interacting with dozens of different fungi. However, quantifying the likelihood of these interactions to take place allows us to faithfully compare, say, whether a plant species is pollinated vs whether it establishes saprophytic-type interactions. Being able to faithfully compare these will be instrumental in what follows.

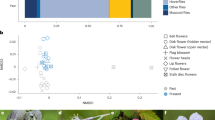
Applied to our ecological data from Na Redona, a visualization of P is available in panels (a) and (b) of Fig. 3. Panel (a) shows that P notably displays a stylized nested structure⁵³. Such pattern—previously known to emerge within the field of ecology in e.g., mutualistic interaction networks^{20,53,54,55,56,57}—is found here when analyzing the participation pattern between plant species and functions. To quantify and assess the statistical significance of such pattern, we used the classical NODF⁵⁸ and its weighted version⁵⁹ (applied to a thresholded binary version of P and to the fully weighted version, respectively) and also built a range of different null models, such as full matrix randomization (EE null model⁵³), or randomization after fixing the degree sequence (FF null model⁵³): see Methods and Supplementary Fig. 2 for details. Results show that P is significantly nested in the topological sense (p value  <0.01 and  <0.03 for null model performing full matrix randomization for NODF and its weighted version, respectively), that both plant species and functions contribute in similar terms to the nested pattern (i.e., both dimensions display heterogeneity), and that nestedness is also significant after fixing the degree sequence in the null model (p value  < 0.05).

Fig. 3: Nestedness in the resource-function matrix of the Na Redona dataset.

In every panel, we use the following acronyms for ecological functions: D for decomposition, H for herbivory, FP for fungal pathogenicity, NU for nutrient uptake, P for pollination, and SD for seed dispersal. a Concrete weighted biadjacency matrix P obtained for the Na Redona dataset, showing a stylized and statistically significant nested structure (see the text and Methods for details). b Visualization of the bipartite (resource-function) network. The nested pattern suggests that plant species participate in different functions in a hierarchical way, and the same applies to functions. Such hierarchy translates to nestedness-based rankings of functions and plant species (c, d, respectively), see Methods and SI for details on the statistical significance of these rankings. P can be pruned according to these rankings, showing a larger-than-random effect on secondary extinctions (see (d) in Figs. 4 and 5). These participation strength-based rankings are further confirmed by other rankings that suitably assess how species connect functions (and vice versa), see Figs. 4c and 5c).

Observing such a nested pattern firstly indicates that the participation of plant species throughout different functions is heterogeneous. To classify species as function-generalists or function-specialists, it is crucial to consider both the number of functions in which they participate and the probability of each participation⁶⁰. Indeed, Fig. 3a shows for instance Withania frutescens and Lavatera maritima participated in all six functions, with high probabilities of 0.7 or greater in many of them, indicating they act as “function-generalist” species. In contrast, others such as Chenopodium murale and Heliotropium europaeum emerge as more “function-specialists”, participating in less functions, and with systematically lower probabilities (0.3 or less). By summing up participation probabilities across functions, we obtain the participation strength of each species i as ${\sum }_{\alpha }{P}_{i}^{\alpha }$. Fig. 3d summarizes a ranking based on the (normalized) participation strength of each species (see also Methods for details). Contrasting this ranking with a suitably defined null model (see Methods for details and Supplementary Fig. 3), we conclude that its precise ordering is statistically significant for the species at the very top of the ranking (Withania frutescens and Lavatera maritima) and those at the very bottom (Chenopodium murale, Heliotropium europaeum and Asparagus horridus), whereas the specific ordering of the middle-ranked species might be the one genuinely found for the Na Redona dataset, but does not necessarily generalize. In Fig. 4d we evaluate how functions are impacted when we remove species from the resource-function matrix in the order prescribed by the ranking. Results confirm that secondary “function extinctions” are systematically larger than a null model, as the extinction curve is systematically above the average null model (the area under the extinction curve is equal to 13—substantially larger than the average area of the null model, which is only about 7.9–, and larger than the null model in ~97% of the randomizations, see SI Supplementary Fig. 4 for additional details). This result opens the door to interpret the species ranking in terms of a ranking of (multifunctional) keystone species. To further confirm these results, in the next section we evaluate the possibility of ranking plant species according not only to how heterogeneously they participate in different functions, but to their role in topologically connecting these functions.

Fig. 4: Phytocentric embedding: function-function networks and multifunctional species keystoneness.

a Function-function network’s weighted adjacency matrix Φ for the Na Redona dataset. b Two examples of conditioned function-function networks Φ∣_i computed by conditioning on the plant species Withania frutescens (bottom) and Heliotropium europaeum (top), showing two cases of plant species with very different multifunctional roles in the ecosystem. Node colors represents each species' relative contribution to the total strength of each function. For a species i, we obtain its contribution to function α relative to that of all species by summing the edge weights (strength) of node i in conditioned function-function network relative to that of all species, which we call multifunctional participation index. Similarly, the color of the edges quantify the weight relative to that of all species along the connections. c Multifunctional species ranking based on enriched metadata of the conditioned function-function networks. In order to rank species, we use the participation indices to obtain its keystone vector (see the text and Methods), which is shown in the figure, color-coded to distinguish contributions from different functions. Species whose score is significantly larger than the respective null model are classified as (multifunctionally) keystone (see the text and Methods). d Pruning analysis of P, plotting the number of secondary function extinctions as a function of the number of perturbed species, performed in the order prescribed by this multifunctional species ranking (c) and the participation strength-based ranking (Fig. 3d), compared to a null model where species are removed at random (see Methods). Both rankings yield very similar extinction curves, which are clearly above the average extinction curve of the null model (see also Supplementary Fig. 7), certifying that the scores on which the rankings predicate to capture a notion of species keystoneness.

Now, by symmetry, the nested pattern also suggests the existence of functions that are “plant-generalist” -meaning they are participated by many plant species with systematic higher probability. Again in panel (a) of Fig. 3 we can see that this is for instance the case of decomposition via saprotrophic fungi, participated by all plant species with high probability in almost all cases. This can then be compared to other functions, which are participated by fewer plant species with considerably lower probability, such as seed dispersal. To describe this variability in participation, Fig. 3c provides a ranking based on the normalized participation strength of each function (see also Supplementary Fig. 3 for a null model and the statistical significance of the position of each of the ranked functions). Figure 5d showcases how removing functions in the order prescribed by this ranking has a larger-than-random impact on secondary species extinctions in the resource-function bipartite network. The extinction curve is always above the average one of the null model, the extinction curve area is larger than the null model average area (27 vs 20) and, even despite the low combinatorics (only six functions), it is larger than 90% of the null model realizations (see Supplementary Fig. 4): removing the resulting top-ranked functions typically have a larger-than-random effect on secondary species extinctions and thus this ranking seems to correlate well with ordering functions in terms of their impact on the system robustness. Similarly as before, this is preliminary evidence pointing that the “hub” functions appearing at the top of the ranking might indeed be “keystone functions”. In the next section we confirm this result by going beyond participation strengths and showing how functions can be ranked according to their role in topologically connecting plant species. It should be emphasized that the new concept of function keystoneness naturally emerges from this framework as a necessary byproduct of observing nestedness in P. Indeed, observing an heterogeneity in function participation directly suggests ranking functions accordingly: we call this result a species-function duality.

Fig. 5: Function-centric embedding: plant-plant networks and multispecies function keystoneness.

a Plant-plant network’s weighted adjacency matrix Π for the Na Redona dataset. b Two examples of conditioned plant-plant networks Π∣^α computed by conditioning on the functions decomposition (top) and seed dispersal (bottom), showing two ecological functions with very different roles as species connectors. c Function ranking based on enriched metadata of the conditioned plant-plant networks (see text and Methods). In the panel, for each function we plot its keystoneness vector (see Methods), color-coded to distinguish contributions from different species. Functions whose score is significantly larger than the respective null model are classified as keystone (see the text and Methods). d Pruning analysis of P, similar to Fig. 4d but plotting now the number of secondary species extinctions as a function of the number of perturbed functions. Both rankings yield the same extinction curve, which is clearly above the average extinction curve of the null model (see also Supplementary Fig. 7), certifying that the scores on which the rankings predicate capture a notion of function keystoneness.

Phytocentric embedding: function-function networks and (multifunctional) keystone species

How do plant species promote effective connections between different functions? Are there plant species that better connect functions? Here, we dive deeper into this question—initially identified in the ranking depicted in Fig. 3d—and assess the role that plants species play as function connectors, eventually bringing about and quantifying the concept of multifunctional species keystoneness. To this aim, we need to build function-function networks, where the link between any two functions is based on the similarity between these two functions with respect to the plant species they participate in, i.e., we need to project functions into a phytocentric embedding. We thus proceed to project the resource-function matrix into the function class and thus extract a function-function effective network with N = 6 nodes and weighted adjacency matrix Φ = P^⊤P (superindex ⊤ denotes matrix transposition) that leverages how species connect functions in the ecosystem. Φ allows for several, mathematically-equivalent interpretations. First, the elements ${\Phi }^{\alpha \beta }={\sum }_{i}{P}_{i}^{\alpha }{P}_{i}^{\beta }$ enumerate the effective paths (passing via a resource-species) connecting two functions α and β, and by weighting such paths, effectively compute the expected number of paths connecting functions α and β. This is therefore based on the number of plant species that simultaneously participate in both functions α and β, and hence quantifies the role of plant species as function connectors. Second, interpreting the different participation probabilities as function features, Φ adopts the mathematical form of a correlation matrix, i.e., a similarity-based matrix, and quantifies how similar functions are to each other based on their participation probability pattern across plant species, i.e., in a plant-feature embedding. See Fig. 4a for a visualization of Φ of the Na Redona dataset, showing that edge weights are indeed heterogeneous, indicating that plant species connect functions in a non-trivial way.

The specific role of species i as a connector of functions can subsequently be disentangled from Φ by conditioning Φ only on a particular plant species i, and then appropriately visualized as a weighted (hexagonal-shaped) 6-node network Φ∣_i, where (i) each node α represents a different function and is enriched with a node weight ${P}_{i}^{\alpha }$ (according to the likelihood that the plant species i participates in that function), (ii) links between pairs of functions α and β denote that plant species i participates in both functions and the link weight ${\Phi }^{\alpha \beta }{| }_{i}:={P}_{i}^{\alpha }{P}_{i}^{\beta }$ quantifies that contribution: see Fig. 4b for some examples and Supplementary Fig. 5 for the complete set of networks {Φ∣_i}. Incidentally, these fall the universality class of rank-1 networks⁶¹ which have been studied under the paradigm of fitness-mediated good-get-richer networks⁶² and hidden variable networks⁶³.

The metadata (properly normalized sets of nodes and edges’ weights) of Φ∣_i informs the (multifunctional) participation pattern of each plant species i in the whole set of ecological functions. Capitalizing on multilayer network theory⁶⁴, we use such metadata to construct a (multifunctional) keystone species score k_species(i) that quantifies the role of each plant species in topologically connecting the different ecological functions (see Methods and Table 1 for mathematical details, Fig. 4c for a species ranking based on such score for the Na Redona dataset, and Supplementary Fig. 6 for details of statistical significance on the resulting ranking). Within this score ranking, species are defined as a multifunctional keystone if their score is larger than the one obtained by a suitable null model up to a certain statistical significance (in this work, above the 90% percentile of the one obtained in the null model). As we can see (Fig. 4c and Supplementary Fig. 6), some plant species such as Withania frutescens or Lavatera maritima are found to be multifunctionally keystone species. In contrast, some other species such as Heliotropium europaeum or Asparagus horridus have scores that are below the 10% percentile of the null model, i.e., their scores are statistically significant, but lie at the bottom of the ranking. This ranking is in very good agreement to the one obtained from the normalized participation strength of species in the resource-function network (Fig. 3d). We have also checked that the term keystone is justified here by analyzing how functions are impacted in the resource-function bipartite network when species are removed in the order provided by this ranking. We found that the functional effect—in terms of secondary extinctions—is systematically larger than expected in a null model (see Fig. 4d and Supplementary Fig. 7). This indicates that these rankings reveal keystone species whose removal have a larger functional impact.

Finally, let us recall that traditional definitions of species keystoneness requires that the relative abundance of such species is not a confounding factor^43,44. We have checked that our (multifunctional) species keystoneness score does not correlate significantly with species relative abundance (Pearson r = 0.31, p value = 0.24) or vegetation cover (Pearson r = 0.47, p value = 0.06) (see Supplementary Fig. 6 and Supplementary Table 1 for statistical details), suggesting that such score is not a simple byproduct of species abundance, but rather indicates a more nuanced property, unveiled here through our formalism.

Function-centric embedding: plant-plant networks and (multispecies) keystone functions

How do functions contribute to connecting plant species? The dual concept of function keystoneness can be explored following similar mathematical manipulations as in the phytocentric perspective: initially starting from the resource-function matrix, we project now into the plant class (function-feature embedding) and thus construct a resource-resource (i.e., plant-plant) effective network with N = 16 nodes and weighted adjacency matrix Π = PP^T, that leverages how functions connect plant resources. Its elements ${\Pi }_{ij}={\sum }_{\alpha }{P}_{i}^{\alpha }{P}_{j}^{\alpha }$ quantify the expected number of shared functions by two plant species, or alternatively how similar two plant species are in a function-feature embedding, see Fig. 5a where we again find that edge weights are heterogeneous. Then, to evaluate and rank the role of each specific function as an ecosystem connector, we replicate the analysis performed before and proceed to disaggregate Π by conditioning on each function, in order to extract 6 different plant-plant networks (one per function α) with weighted adjacency matrices Π∣^α, with elements ${\Pi }_{ij}{| }^{\alpha }={P}_{i}^{\alpha }{P}_{j}^{\alpha }$ (see Fig. 5b for some examples and Supplementary Fig. 7 for the complete set {Π∣^α}). From the metadata of Π∣^α we can thus build a (multispecies) keystone score for each function (see Methods and Table 1 for details, Fig. 5c for a ranking of functions based on such score in the Na Redona dataset, and Methods and Supplementary Fig. 5 for details on null models and statistical significance of these scores). This ranking is in good agreement with the one based on normalized participation strength in the resource-function matrix (Fig. 3c), and certifies that decomposition stands out in a statistically significant position, whereas seed dispersal appears to be an ecological function with a (statistically significant) smaller role in connecting plant species than expected. Removing functions in P in the order provided by this ranking once again demonstrated a greater-than-random impact on secondary species extinctions (see Fig. 5d and Supplementary Fig. 7). This suggests that this ranking identifies aspects of system resilience and therefore the term keystone function is reasonably justified.

Discussion

The RCF tensor we have presented facilitates data standardization and notation, by incorporating the interaction of species via different ecological functions into a resource-consumer(-function) paradigm. This offers a possible working solution for Challenge 1 on the matter of having a single and flexible modeling framework, as presented in the Introduction. Such RCF indeed offers flexible visualizations in terms of multilayer networks (Fig. 2). Observe at this point that the RCF is a rank-3 tensor, while standard tensorial formulations of multilayer networks are generally rank-4 tensors²⁸ (two indices for interacting nodes, and two indices characterizing the layer in which each node is located). The difference stems from the fact that in our case—and, to some extent, in multilayer ecological networks more generally—three indices are enough.

Ecological interpretation of the results

The reduction of the RCF tensor into a resource-function matrix provides valuable insights into how resources (plant species) and ecological functions are intertwined within the ecosystem. The Na Redona case unveils the emergence of a (statistically significant) non-random, nested pattern in the way resources and functions participate with each other. While future work should confirm whether this pattern holds for other ecosystems, it is interesting to remark that many previous works have related the onset of nested structures in (single-function, species-species) ecological networks with important aspects of ecosystem functioning such as robustness, coextinction cascades, stability, feasibility or sustainment of biodiversity: see ref. ⁵³ and references therein. Our framework and data thus open the possibility to investigate similar questions in the multilayer networks, e.g., would allow us to potentially link multifunctionality and biodiversity.

Subsequently, unfolding the species-function matrix allowed us to propose a measure of species keystoneness, specifically based on the fact that the ecosystem harbors different types of ecological interactions and that different species (i) participate in, and (ii) indirectly connect different ecological functions. Observe that the traditional definition of a keystone species^{43,44,45,46,47}—species disproportionately important for community functioning, regardless of their abundance—is deliberately vague as it relies on the multifaceted concept of “community functioning”, and thus allows for different mathematizations depending on the particular facet of the community. In this sense, here we have focused on the concomitant effect of considering at the same time different ecological functions⁴⁸, and have accordingly extended the concept of keystone species to a multifunctional one, that takes into account two topological properties: (i) the species participation in different ecological functions and (ii) how well the species indirectly connect different ecological functions. The resulting scores and their rankings (Figs. 3d and. 4c) are indeed in good agreement with each other (Supplementary Fig. 8 further confirms that species abundance is not a confounding factor in these rankings). Additionally, an extinction analysis performed on the resource-function matrix (Fig. 4d and Supplementary Figs. 4 and 7) shows that a larger-than-random effect is observed on secondary extinctions when removing species or perturbing functions in the order prescribed by these rankings. This is our interpretation of the “disproportional importance for community functioning” of a keystone actor and justifies that our species rankings can be interpreted as such.

In the Na Redona islet, these rankings indicate that plant species contribute heterogeneously to multiple ecosystem functions, i.e., they multitask⁴⁸. Interestingly, the first six species in the rankings, i.e., those with the highest keystone scores, are all woody shrubs. Within that set, the first two species Withania frutescens and Lavatera maritima are indeed multifunctionally keystone (having a score significantly larger than a null model). The rest, except for Ephedra fragilis, are all herbaceous. Now, herbs such as Chenopodium murale and Heliotropium europaeum, with keystone scores significantly smaller than a null model, appear to play a minor role in connecting different functions. Their presence suggests that these species have a very concrete role—e.g., are probably important for very particular ecological functions.

The finding that woody shrubs are those more strongly involved in different functions might be attributed to the longer lifespan of such species compared to herbs, which allows them to link to a wider array of species in each type of interaction. However, more in-depth studies are needed to unveil the exact mechanism of such multitasking. Interactions between plants and fungi (especially saprotrophic and pathogenic fungi) were found to play a salient role. Microbial decomposers, together with plants and herbivorous insects, are also important drivers of ecosystem functioning in grasslands, where a positive association has been documented between richness or abundance and multiple ecosystem services⁶⁵.

We have also introduced the concept of keystone function—that, to the best of our knowledge, had gone unnoticed to date. This concept emerges naturally thanks to the species-function duality observed in the resource-function matrix. Operationally, in this work we called a function keystone when (i) the scores based on their participation by different plant species (Fig. 3c) and the scores based on their role indirectly connecting species (Fig. 5c) were in agreement and larger than the 90th percentile scores of suitable null models (Supplementary Figs. 3 and 6), and when (ii) the effect of perturbing functions on secondary species extinction in the order prescribed by these scores were (statistically significantly) larger-than-random (Fig. 5d and Supplementary Figs. 4 and 7). We propose that this new concept aligns with approaching the ecosystem through a function-centric lens, rather than a traditional species-centric (e.g., phytocentric) one. Indeed, just as robustness and resilience in the face of a disturbance is usually calculated at the species level⁶⁶, it is also possible to assess such responses of the ecosystem at the functional level: the response of the ecosystem to some disturbances may overall affect entire functions. For instance, non-native herbivores can disrupt chemically-mediated interactions between plants and herbivores, pollinators, predators, and parasites that respond to herbivore-induced plant volatile cues⁶⁷. Because there is a wide variety of interactions involving native organisms that a single non-native could potentially impact, defining and identifying key ecological functions is a crucial first step toward better understanding their role in ecosystem development, balance, functioning, and resilience¹⁵.

In the Na Redona islet, our results indicate that fungi-led interactions are more widespread. More specifically, saprophytic-type interactions exhibit a disproportionate prevalence, and decomposition emerges as the only keystone function, in both rankings (Figs. 3c and 5c). While such a result should be confirmed for other ecosystems, at this point, we can comment that this is in agreement with a relatively recent shift in the interest and relevance of underground -in contrast to above-ground- interactions within ecosystem functioning⁶⁸. On the other hand, in our database seed dispersal is found to have a significantly low score. In hindsight, this specific result can be related to the fact that Na Redona is an islet with a shortage of plants with fleshy fruits, and in this sense, in other ecosystems where the abundance of fleshy fruits is higher, the score of seed dispersal might be larger.

In any case, understanding the origin for the presence of actors with disproportionally (and statistically significant) low keystone scores—such as the case of seed dispersal in Na Redona—and why species or functions with apparently weaker connecting roles are still observed in the ecosystem is reminiscent of similar questions on the rare biosphere: low-abundance microbial populations that in turn display specific and sometimes unique ecology and serve as a broad reservoir of ecological resiliency⁶⁹.

Observe that finding (statistically significant) heterogeneous keystone scores both for plant species and functions essentially means that there are some plant species and functions (those considered keystone) for which the number of observed indirect connections to other species and functions is enhanced with respect to a null model. Interestingly, previous works have found that indirect effects between species are more likely to predominate in nested networks³, and impacts species fitness⁷⁰. In our context, our findings open the door to (i) relate the structure of indirect species-species relations (Π) to e.g., biodiversity maintenance, but also (ii) investigate the impact of indirect function-function relations (Φ) on similar ecological questions.

Finally, it is worth noting that our whole framework is in principle metric-agnostic. While we used some specific quantification metrics, other complementary ones are also possible⁷¹: for instance, participation strengths—instead of participation probabilities—could also be built by summing up contributions of ${f}_{ix}^{\alpha }$, rather than by building ${P}_{i}^{\alpha }$ via Eq. (1). However, as already anticipated, there is a merit in building scores from ${P}_{i}^{\alpha }$, as these are probabilities and are therefore not severely affected by potential sampling biases (see also below).

Limitations

Now, it is important to acknowledge that there are certain limitations to our analysis and methodology, mainly associated with the unavoidable specifics of data collected in the Na Redona islet, that we synthesize in five points. First, our fieldwork observations were in principle designed so as to link different interaction types with different ecological functions (see Methods). We acknowledge that such mapping could be debatable, specially the mapping of fungal interactions to functions, as there is a shortage of literature on the specific function associated to fungal interactions, and more work is needed in this aspect. Second, the particular mathematical method we used to integrate out consumers in the RCF tensor is based on the fact that in each layer (e.g., for each function), the interactions are bipartite; that is, there are no direct interactions between plants or between animals/fungi. Consequently, incorporating competition between plants and/or animals/fungi would require either to add more indices in the tensor, or to express it as ${f}_{ij}^{\alpha }$, where now both i and j are indices that run both over resources and consumers alike, i.e., the partition between resources and consumers would be obscured. Third, while multifunctional, our collected data is eminently phytocentric (centered in observing plant species), instead of zoocentric (centered in observing consumers—animals, insects, etc.–). If newer data allows us to account for purely zoocentric observations (ideally mixed phyto-zoo-centric observations), retaining the complete RCF tensor would be convenient instead of integrating out the consumer index, and direct manipulation of the RCF tensor would easily follow (for instance, allowing to assess consumer-function participation patterns as well). Fourth, since again field observations were focused primarily on plants, we also lack specific information, such as the trajectory of insect pollinators. Consequently, we cannot directly quantify the probability that a plant is included in the diet of a particular insect pollinator species. In this case, the parsimonious approach is to assume independence, and this is the base of our derivations. However, the contribution of a plant species to a function is typically mediated by the participation of several animal/fungal taxa, and the existence of correlations in the behavior of different species is possible. Take for example, again, pollination. In our calculations, we assumed that a universal probability governs whether a specific plant is visited or not. However, we do know that plants may attract specific pollinator species (specially the most specialized ones that have particular flower traits, e.g., long corolla tubes), resulting in a latent correlation kernel. Accordingly, the advent of new data should be used to test the validity of our parsimonious assumption. And lastly fifth, even if the sampling effort and the sampling protocol for each function were carefully designed and followed the standard guidelines of the field (see Methods), all fieldwork data probably (and unavoidably) suffers from some sampling and observational biases in the consumer index (possibly except fungi-mediated interactions, which are easier to observe as these are static and observations are subsequently resolved via genetic techniques). Comparing to, say, insect-mediated ones, which are by design more difficult to observe, a logical consequence is that, in the multilayer ecological network, the layers associated to fungal interactions have substantially more consumer nodes than other layers. Further fieldwork efforts are needed to quantify and control these uncertainties and to confirm the generality of our results. That being said, we explicitly were able to alleviate some of these biases by quantifying resource-function participation using probabilities of observing such events (${P}_{i}^{\alpha }$), instead of using (more traditional) raw weights that measure the actual number of observed occurrences.

Final remarks

While applied in an ecological context, this framework is conceptually general and can be easily extended to characterize e.g., the interplay between resources and functions in other complex systems. For instance, it can be applied to genetics, where our resource-function mapping resembles a classical genotype-phenotype map⁷², illustrating how genes interact to give rise to phenotypes in various animals. Similarly, in economic systems, this interplay can shed light on how goods are traded among countries across different economic sectors⁷³. Going back to the ecological case, the resource-function matrix (and its projections Φ and Π) unveils the duality of plant species and functions (phyto vs function-centric perspectives), where the concept of (multifunctional) keystone species and the concept of (multispecies) keystone functions naturally emerge as two (interconnected) sides of the same coin. The former refers to species that play key roles in connecting functions in a multifunctional system -with possible impact on e.g., network stability⁴⁸-. In contrast, the latter refers to the different roles functions play in keeping species coexistence in an ecosystem. Our initial assessment in the Na Redona dataset shows that a drastic perturbation of keystone species^51,74 propagate into functions (via secondary “function extinctions”) more than expected at random, and the opposite is true when perturbing keystone functions. While further work is needed to refine these results (e.g., perturbing species gradually instead of abruptly would be interesting to assess the impact of losing pollinators on fruit production), our findings indicate that both concepts (species and functions) are indeed intertwined, potentially feeding back into each other. For instance, in the context of climate change, it is not uncommon to witness drastic and sustained temperature increases over large geographic regions. If such exogenous perturbations induce, e.g., phenological mismatches between flowering plants and insect pollinator visits, then the complete pollination function might be threatened before any of the species are themselves threatened^75,76, i.e., perturbation takes place initially at the function level. It can then propagate with potential cascading effects for both species and other functions, as prescribed by the resource-function matrix P. Conversely, the decline or extinction of a seed disperser (initially at the animal species level) may trigger declines or plant extinctions, which in turn cascade to affect species involved in other functions, such as underground fungi⁷⁷. Furthermore, the extinction of a keystone plant species can also influence other species’ interactions, either by causing interaction rewiring or by modifying interaction strengths^{78,79,80,81,82}. Such cascading effects across interaction types become particularly problematic in double-mutualistic interactions, i.e., when the same animal acts, for example, as pollinator and seed disperser of the same plant species¹¹. Yet, not only the disruption of mutualistic interactions but also of antagonistic interactions could derive functional losses, e.g., the loss of top predators may indirectly affect ecosystem productivity and metabolism⁸³. However, few studies still exist on how human activities can alter ecosystem multifunctionality, both directly on ecosystems and indirectly through the loss of multifunctional biodiversity^32,84. Moreover, how organisms at different trophic levels interact to influence ecosystem multifunctionality in the presence of multiple concurrent anthropogenic drivers remains largely unexplored^65,85. Thus, we hope our framework offers a promising approach for evaluating the relative vulnerability of ecosystem functions to anthropogenic stressors. As we delve deeper into understanding ecosystems, the integration of temporal, spatial, and dynamical features within this framework, coupled with its application to ecological data from other environments, also emerges as exciting avenues for future research.

Methods

This research complies with all relevant ethical regulations. The study protocol was reviewed and approved by the Ethics Committee of the Spanish National Research Council (CSIC). The approval number for this study is [CGL2017-88122-P, PID2020-114324GB-C21], and the protocol adheres to the ethical guidelines outlined by the IRB.

Study site and field sampling

The fieldwork was carried out on Na Redona (39° 10′ 5′′ N, 2° 58′ 35′′ E), an islet of approximately 11ha and 56m high in the Cabrera Archipelago National Park (Balearic Islands, Western Mediterranean Sea). Its primary habitat is Mediterranean shrubland with a relatively rich plant species diversity (ca. 108). Fieldwork, including the sampling and capture of lizards and birds, was conducted in accordance with permits issued by the Cabrera Archipelago National Park authorities. The permit numbers are SEN 184/18, SEN 074/19, SEN 687/2020, and the research activities were carried out under strict adherence to the guidelines and conditions set forth by the National Park authorities to ensure minimal impact on the local wildlife and habitat. Birds were captured by R.H., who is licensed (221/2019) by the Instituto da Conservação da Natureza e das Florestas (ICNF, Portugal). Lizards were captured by M.N., who is licensed (CAP-169.4-20) by the Dirección General de Agricultura, Ganadería y Alimentación (Spain).

In two contrasting seasons, a team of five people visited the islet for five consecutive days at the peak of flowering (April/May) and at the peak of fruiting (October/November), to sample the different types of interactions between plants and (1) pollinators, (2) herbivores, (3) seed dispersers, and root-colonizing (4) saprotrophic, (5) symbiotic, and (6) pathogenic fungi. In each sampling season, six transects (100 m long × 10m wide and separated from each other by at least 100 m) were established to cover the main microhabitats and the entire altitudinal gradient of the island. In such transects, we assessed plant abundance (number of individuals) and vegetation cover (m²) of each plant species, and we recorded all species interactions except the seed dispersal ones (see below).

Plant/fungus interactions were sampled by collecting the roots of five individuals of each plant species along the transects. Dry-cleaned roots were immediately preserved in silica gel until processing for DNA extraction. Then, PCR amplification was performed using fungal-targeted primers ITS1f (5′-CTTGGTCATTTAGAGGAAGTAA-3′) and ITS2 (5′-GCTGCGTTCTTCATCGATGC-3′)^86,87. PCR products were cleaned, quantified, and sequenced at an equimolar concentration (Illumina sequencing using 2 × 350 bp MiSeq) at GENYO (University of Granada, Spain). Reads were filtered and processed using QIIME 2 pipeline⁸⁸, and assigned to fungal ASV (amplicon sequence variants) using DADA2⁸⁹. Taxonomy and functional groups were determined using the UNITE database⁹⁰ and FUNGuild⁹¹.

To sample plant-pollinator interactions, we follow a standard protocol to accurately estimate flower visitation rates^11,92: we conducted censuses (of 10 min of duration, and at different times of the day) consisting of direct observations on each plant individual. Each species was observed for at least one hour during the sampling season, although the total time depended on flower availability (mean = 2 h, total sampling effort across species = 29 h). In each census, we recorded any animal (i.e., insects, lizards, or/and birds) that contacted the reproductive parts of the flowers. Insect species were photographed and identified using the reference collection available at IMEDEA. When unknown, they were captured and later identified by an entomologist, to the species level when possible or to the morphospecies level otherwise. Additionally, we captured 30 lizards using a noose on the tip, and 26 land birds using mist nets, being the latter not very abundant and difficult to catch since the islet is dominated by open vegetation and/or shrublands. We sampled the potential pollen carried by each lizard and bird by swabbing a cube (~3 mm³) of fuchsine-stained glycerin jelly on their snout, and beak and peri-mandibular feathers, respectively. The gelatine cube was then placed on a microscope slide, melted, and covered with a slip. The entire slide area was inspected under a light microscope to identify and count all pollen grains to species level using a pollen reference collection available at IMEDEA. Evidence of flower visitation was considered if more than six pollen grains of a given plant species were detected in the sample. Each captured individual was considered a sampling unit.

Plant-herbivore interactions were evaluated in five individuals of each plant species, browsing the isolated branches and recording all arthropods found feeding on plant tissues. Unknown herbivorous species were captured and later identified by an entomologist, to the species level when possible or to the morphospecies level otherwise.

Finally, to sample plant-seed disperser interactions¹¹, we collected droppings and pellets of gulls (236), droppings of passerines (21), and lizards (375), and anthill material (4). We identified all taxa to plant species level or morphospecies under a stereomicroscope, by comparing the seeds with a reference seed collection also available at IMEDEA.

Estimation of the weights in the RCF tensor

Taking advantage of the simplicity of a small island, we focus on six different types of ecological interactions, that in this work, we categorize into six different ecological functions: pollination, herbivory, seed dispersal, decomposition of organic matter, nutrient uptake (mycorrhizas) and fungal pathogenicity. Accordingly, we assume a one-to-one map from interaction type to function:

Plant-pollinator interaction ⇔ Pollination

Plant-herbivore interaction ⇔ Herbivory

Plant-seed disperser interaction ⇔ Seed dispersal

Plant-saprotrophic fungi interaction ⇔ Decomposition

Plant-symbiotic fungi interaction ⇔ (fungal) Nutrient Uptake

Plant-pathogenic fungi interaction ⇔ Fungal Pathogenicity

Saprotrophic fungi are the primary agents of plant litter decomposition, thus, key regulators of nutrient cycling. Saprotrophic fungi play a key role in terrestrial ecosystems as they regulate nutrient and carbon cycles, influencing soil structure and ecosystem multifunctionality. Up to 80% of plant N and P is provided by mycorrhizal fungi and many plant species depend on these symbionts for growth and survival. Fungal pathogenicity is not a standard ecological function per se but can impact functions and processes through its effects on population dynamics, biodiversity, trophic interactions, nutrient cycling, succession, and co-evolution. Understanding the interactions between fungal pathogens and their hosts is indeed important for comprehending and managing the ecological consequences of these diseases^93,94. Our common species in six layers are plants (“resources”), and we study their interactions with “consumers”: (1) pollinators, (2) herbivores, (3) seed dispersers, (4) saprotrophic, (5) symbiotic and (6) pathogenic fungi.

Every time an interaction is recorded, the type of function it belongs to is also annotated -leaving no room for ambiguity- regardless of e.g., the time elapsed in the interaction, so the effective weight of such interaction is given through the estimation of the probability of observing such event (the observed proportion of the sampled population participating of that type of interaction). Now, we acknowledge that these choices are not unique. For instance, the relation between interaction type and ecological function is indeed not necessarily bijective. Furthermore, not annotating elapsed time of the interaction is probably inducing a loss of information (at the expense of allowing for fair comparisons). In this sense, we also acknowledge the role of inherently weak interactions in ecology, as they can act as both stabilizing factors and drivers of unstable dynamics^95,96 and that our choice does not allow us to evaluate this as it does not account for the variability in inherent interaction strength.

Estimation for phytocentrically observed interactions

Let ${m}_{ix}^{\alpha }$ be the number of individuals of plant species i on which (at least one individual of) an animal species x was observed interacting via a certain ecological function α, and let n_i be the number of individuals of such plant species i that were sampled overall. Then, the observed probability ${f}_{ix}^{\alpha }$ of such interaction between plant species i and animal species x at function α was calculated as

$${f}_{ix}^{\alpha }=\frac{{m}_{ix}^{\alpha }}{{n}_{i}}.$$

For illustration, if say a total of n_i  = 20 samples of the plant species i were monitored, and 12 of them were observed being pollinated by a single animal species, whereas 10 of them were observed being dispersed (7 by animal species 1 and 3 by animal species 2), then the associated probabilities ${f}_{ix}^{\alpha }$ would be 12/20, 7/20, and 3/20 respectively (observe that these don’t add up to one: events are independent and thus probabilities are only normalized in terms of an event and its complementary). For example, in the case of the pollination layer, the weights of the interaction measure the fraction of plants of a given species that have been observed being pollinated, in other words, the probability that a random plant of species i is being pollinated. Plant-fungus interactions were quantified as the proportion of different ASV reads per plant species⁹⁷.

Estimation for zoo-centrically observed interactions

The case of seed dispersal is slightly different than the rest of functions, as the associated interactions are not recorded by tracking plant species, but here by tracking disperser animals. Accordingly, ${f}_{ix}^{\alpha }$ is estimated in this case as the proportion of all droppings of a given species x where seeds of plant species i were found.

RCF visualization

The specific visualization of the RCF tensor presented in Fig. 2, containing plant species and the weight of interactions with animal/fungus species, was obtained using Netgraph, a freely available library implemented in Python (https://github.com/paulbrodersen/netgraph, last accessed: 10 March 2023). This layout also incorporates a study of the mesoscale organization of the RCF while considering the network as a single-layer one. For that purpose, we used Infomap, a network clustering algorithm based on the Map Equation freely available at (https://github.com/mapequation/infomap.git, last accessed: 10 March 2023). The same clusters were also found using an alternative method (Louvain community detection algorithm). Generally, a plant species interacts with an animal/fungus species through a single function. By projecting the tensor/multigraph onto a single layer, we focus the community detection algorithm’s attention on the plant-animal/fungi interactions. This allowed us to visualize 15 clusters, which broadly group the plant-animal/fungus pairs with the strongest interactions. We used different colors to identify each type of interaction and its associated animal/fungus species. For other visualizations, including Infomap enriched with multilayer properties, see Supplementary Fig. 1.

Within our data, only three interactions between a plant species i and an animal/fungus x were cataloged as belonging to two different functions. This happens, for example, when an insect exhibits herbivory during its larval stage and pollination during its adult stage. These interactions are represented as multilinks in the RCF, and are visualized with corresponding colors in the network without overlapping. Colors are assigned to the animal/fungus nodes based on one of the interactions, with a border of the color corresponding to the other interaction.

Estimation of edge weights ${P}_{i}^{\alpha }$

To integrate our animals in the RCF tensor and build the multilayer ecological network, we follow a simple logical manipulation of probabilities. By construction, in the RCF the weight ${f}_{ix}^{\alpha }$ is the probability of finding a specific resource i and a specific animal/fungus x interacting via a specific function α, thus $1-{f}_{ix}^{\alpha }$ (the negation) is the probability of not finding (a specific resource i and a specific animal/fungus x interacting via a specific function α). Assuming independence of events, the probability of not finding a specific resource i and any animal/fungus x interacting via a specific function α is, consequently, ${\prod }_{x}(1-{f}_{ix}^{\alpha })$, where ∏_x is the product symbol, running over index x. We finally negate this again, so the probability of finding a specific resource i and any animal/fungus x interacting via a specific function α is $1-{\prod }_{x}{f}_{ix}^{\alpha }$, recovering Eq. (1) in the main text. Observe that this probability is independent of x, it just describes the probability of a resource i “effectively interacting” via a function α, i.e., the probability that a plant species i participates in a function α. We called this the participation probability ${P}_{i}^{\alpha }$.

Nestedness quantification and null models

There exists a variety of ways to quantify nestedness and to assess its statistical significance via null models⁵³. Here we make use of the NODF procedure⁵⁸, and its weighted version⁵⁹. We assess the statistical significance of the metrics by building two types of null models. Null models based on full randomization of the matrix (null model 1, also called EE in ref. ⁵³) preserve the total number of links (and total strength in the case of the weighted version), but not the degree of individual nodes (or their individual weight), and thus aim at checking whether the observed nestedness value can be explained solely by the degree. This is sometimes considered the less restrictive null model⁵³. A much more conservative null model (actually considered the most restrictive⁵³) is based on link swapping of non-null entries (null model 2, also called FF in ref. ⁵³). This null model preserves the degree sequence of each node (i.e., fixes the position of all non-null weights and proceeds to randomly swap weights in the remaining entries) and thus aims at checking whether the observed nestedness value can be explained solely by the topological heterogeneity induced by the degree sequence. Accordingly, finding statistical significance of nestedness-based on null model 1 but finding lack of statistical significance based on null model 2 indicates that the matrix is nested in the topological sense—i.e., such property is due to the wiring architecture–, but specific node strengths are not themselves significantly contributing to the pattern. This is, for instance, what has been observed in a large set of cases⁵³. Finding statistical significance based on both null models means that not only the nested pattern is a topological one, but also the precise weights are nested. In our case, we found that P is significantly nested according to both NODF and WNODF with respect to null model 1, finding p values of ~10⁻⁴ for NODF (when using different binarization thresholds, the p value fluctuates, but is systematically smaller than 0.01, see Supplementary Fig. 2) and p < 0.03 for WNODF. Moreover, we also found that P is significantly nested according to null model 2 (p value <0.05).

Generalist-specialist ranking and its null model

The ranking of generalist and specialist species and functions in the bipartite network with biadjacency matrix P is based on ordering species and functions according to their (normalized) participation strength, which we now define. In P, the strength of a node is the sum of the weights of all incident links to that node. For instance, a given function α has participation strength ${\sum }_{i}{P}_{i}^{\alpha }$. We then normalize this magnitude over all functions to reach a normalized participation strength

$$s(\alpha )=\frac{{\sum }_{i}{P}_{i}^{\alpha }}{{\sum }_{\alpha }{\sum }_{i}{P}_{i}^{\alpha }}.$$

The normalized participation strength of each plant species is computed following a similar procedure, e.g., the participation strength of a species i is ${\sum }_{\alpha }{P}_{i}^{\alpha }$ and normalization over all species is subsequently performed. Finally, we rank functions and species by sorting in decreasing order their normalized participation strengths.

To assess the statistical significance of such ranking, we build a null model consisting of an ensemble of 10⁴ randomizations of P (where entries of P are shuffled and the constraint of P being connected is required). Such randomization thus preserves the total number of links and total strength, but not the specific node participation strengths. In each individual randomization we compute the normalized participation strengths of plant species ${\{s(i)\}}_{i=1}^{16}$ and functions ${\{s(\alpha )\}}_{\alpha=1}^{6}$, and compare, for each one, the mean and standard deviation of the ensemble with respect to the one found for P. Any entry whose normalized participation strength is outside the region between the 10% and the 90% percentile of the values found in the null model is assumed to be “statistically significant”, meaning that the specific ranking of such entry cannot be explained solely based on the total strength of the resource-function matrix. For those entries whose normalized participation strength falls within the 10–90 percentile region of the null model, we conclude that the ranking observed in the Na Redona dataset might not be robust. See Supplementary Fig. 3 for details.

Multilayer participation indices, keystoneness scores, and their null model

We capitalize multilayer network theory to quantify the importance of resource i in connecting functions in terms of the so-called multilayer participation index⁶⁴. Applied to our context, after a little algebra we find that the multilayer participation index of plant species i in function α, MPI(i, α) is

$${{{\rm{MPI}}}}(i,\alpha )=\frac{{\sum }_{\beta }{P}_{i}^{\alpha }{P}_{i}^{\beta }}{{\sum }_{j}{\sum }_{\beta }{P}_{j}^{\alpha }{P}_{j}^{\beta }}=\frac{{\left.{\sum }_{\beta }{\Phi }^{\alpha \beta }\right\vert }_{i}}{{\left.{\sum }_{j}{\sum }_{\beta }{\Phi }^{\alpha \beta }\right\vert }_{j}}=\frac{{\left.{\sum }_{\beta }{\Phi }^{\alpha \beta }\right\vert }_{i}}{{\sum }_{\beta }{\Phi }^{\alpha \beta }},$$

where j runs over plant species.

The resulting keystoneness vector of plant species i is composed of the 6 MPIs (MPI(i, 1), MPI(i, 2), …, MPI(i, 6)), one element for each function (each of these MPIs is color-coded in Fig. 4d). The L₁-norm of such vector (since it is positively defined, it’s just the sum of all entries) provides the species keystoneness score k_species(i):

$${k}_{{{{\rm{species}}}}}(i)=\left| \left| ({{{\rm{MPI}}}}(i,1),{{{\rm{MPI}}}}(i,2),\ldots,{{{\rm{MPI}}}}(i,6))\right| \right| _{1}={\sum}_{\alpha }{{{\rm{MPI}}}}(i,\alpha )$$

Sorting species in order of decreasing keystoneness provides the ranking displayed in Fig. 4d.

Interpretation: In MPI(i, α), the numerator is easily interpreted as the strength of the topological connection between a given function α and the rest of the functions, where such connection is facilitated via the participation of species i (the denominator is just a normalization factor). Summing over all functions α we then reach k_species(i), which provides the aggregated (normalized) strength of species i in connecting all functions.

The same methodology is reproduced in the function-centric case to first compute a multilayer participation index of function α in plant species i, mPI(α, i), as

$${{{\rm{mPI}}}}(\alpha,i)=\frac{{\left.{\sum }_{j}{\Pi }_{ij}\right\vert }^{\alpha }}{{\sum }_{j}{\Pi }_{ij}},$$

the keystoneness vector of function α (composed of the 16 respective MPIs, one for each plant species, color-coded in Fig. 5d), and a function keystoneness score k_function(α)

$${k}_{{{{\rm{function}}}}}(\alpha )=\left| \left| ({{{\rm{mPI}}}}(1,\alpha ),{{{\rm{mPI}}}}(2,\alpha ),\ldots,{{{\rm{mPI}}}}(16,\alpha ))\right| \right| _{1}={\sum}_{i}{{{\rm{mPI}}}}(\alpha,i)$$

that allows us to rank functions accordingly (Fig. 4d). The statistical significance of these rankings is checked based on a null model similar to the one developed for the generalist-specialist ranking, where we construct the 10–90 percentile region of scored obtained in the null model. Species and functions whose score is above the 90% percentile of the null model are defined as significant keystone (see Supplementary Fig. 5).

Extinction curves analysis

To assess the impact of perturbing species or functions in the order prescribed by a specific ranking, we consider the resource-function bipartite network P and proceed to remove sequentially these nodes (either the species or the functions). At the same time, we track the number of extinct nodes (nodes from the other group that suffer a secondary extinction⁷⁴). The extinction curve gives the total number of secondary extinct species/functions as the number of removed species/functions increases. The area under this curve (essentially, the cumulated sum of extinct species/functions) is larger when nodes are removed in order of higher to lower importance for the network’s resilience. To interpret the results, we build a null model where the same quantities (extinction curve and the area under the curve) are computed for random orderings (10³ random orderings for the case of removing species, and all 6! = 720 orderings for the case of removing functions). From the null model, we build the average extinction curve of the null model (displayed in Figs. 4d and 5d alongside the actual extinction curves), and we extract the extinction area probability distribution for the null model. Supplementary Figs. 4 and 9 display these distributions for each of the rankings, highlighting that the observed extinction area is systematically larger than the extinction area of a null model. The percentage of random orderings resulting in an extinction area equal or larger to the one obtained for the ranking under analysis is akin to a p value.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.