Introduction

Nanoporous materials such as zeolites1, metal-organic frameworks (MOFs)2,3 and covalent-organic frameworks (COFs)4 hold substantial importance in applications involving chemical storage, separation and catalytic conversions. The significance of these nanoporous materials has grown significantly5,6; especially since they offer sustainable, energy economic and low carbon footprint technologies, e.g membrane based chemical separation7,8,9. In these practical contexts, the prevalent factor influencing efficiency is molecular diffusion8,10,11,12. The movement of the molecules through chemically functionalized channels of the nanoporous materials is influenced by various factors, including chemical interactions (adsorbate-adsorbent), concentration gradient, channel size and shape12. Occasionally, using imaging13 and spectroscopic techniques14 it has been possible to visualize the molecular diffusion path12. However, modulation of diffusion and subsequent manipulation of material properties pose significantly greater challenges.

Among the nanoporous materials, MOFs are crystalline, versatile topology, high porosity (surface area >7000 m2/g) material and well-known for chemical storage, separation15,16, sensing17 and catalysis18,19 applications. A great number of literatures reflect applicability of MOFs as functional nanoporous material, and also the successful chemical design strategies that have improved their performance. Notably, while many of the synthesized MOFs excel in adsorption-based separation (i.e. at equilibrium)15, relatively a few serve as membranes (~1% of the all known MOFs)9,20, relying on differences in diffusivity for separation. The reason of relatively fewer selected MOFs for membrane based separation is (apart from processibility issues) that a predictive design of pore geometry and functionality for diffusion control is far more challenging than the adsorption process21,22. For the heterogeneous catalysis too, role of substrate diffusivity is not well investigated. One mechanism of overcoming this challenge is to develop a computational screening approach. By simulating molecular diffusion within MOF pores, not only may the sampling volume can be accelerated, but it can also offer insights into the interactions between the adsorbate and MOF (thermodynamic and kinetic)23,24,25. Utilizing knowledge of diffusivity and interactions, it becomes feasible to tailor porous materials to exhibit targeted molecular diffusion, facilitating chemical separation and catalysis. While the computational screening approaches for MOF-membrane design have received a significant interest26,27, experimental manipulation of diffusivity has remained challenging. Recent experimental efforts, such as downsizing MOF crystallite size, morphology control28, controlling nanochannel orientation29,30,31 and employing heterostructure design32,33,34,35,36 improve molecular diffusivity, however do not predictively tune the diffusivity.

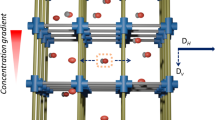
It is evident that for controlling molecular diffusion, a comprehensive strategy to assess the thermodynamics and kinetics is much needed. In this communication, we have employed a strategy incorporating both precise measurement of mass uptake kinetics and molecular dynamic (MD) simulation. This approach was applied within a specifically designed and functionalized nanochannel of (pillared-layer) MOF thin film to understand and regulate molecular diffusion of chemical isomers. Our findings confirm that MOF nanochannel orientation, distribution of chemical functionality on the pore surface and framework dynamics work in tandem to regulate molecular diffusion rate and direction. Leveraging these insights, we establish an adsorbate-MOF “dynamic chemical interaction”. The dynamic interactions profoundly influence molecular diffusion; as we evidence, certain linker-adsorbate interactions can enhance or hinder diffusion on the basis of framework dynamics. In the following discussion, we have illustrated a chemical strategy to implement the “dynamic chemical interaction” and utilizing this we have achieved a reversal of diffusion selectivity for 1 and 2-bromopropane (1BP and 2BP) positional isomers in the nanoporous MOF thin film (Fig. 1).

Fig. 1: Dynamic chemical interaction.
figure 1

A schematic illustration of the dynamic chemical functionalities in oriented nanoporous metal-organic framework thin film; introduction of dynamic chemical interaction between the chemical isomers (shown as green and orange spheres) and MOF reverses the diffusion selectivity; cube = metal-oxo node, hexagonal blocks and cylinders = linkers and pillars in the MOF structure. Diffusion is along the concentration gradient, i.e. along [001] in the studied MOF structure.

Full size image

Results

The various factors governing molecular diffusion in MOFs include: (i) pore window and cavity size, (ii) orientation of nanochannels, (iii) distribution of chemical functionality on the pore surface, (iv) adsorption enthalpy and (v) linker/framework flexibility12. Although these factors are well recognized, combined effect of these are challenging to perceive and implement. We have considered each of these factors to design a MOF thin film and study the diffusion selectivity of 1BP and 2BP isomers. The halogenated alkane isomers are commercially important chemical feedstocks (for lubricants, pesticides, PVC production)37 and very few studies highlighted the possibility of adsorptive separation of these isomers38. We chose the brominated isomers as a proof of concept to demonstrate the potential of “dynamic chemical interaction”. Firstly, we outline the design strategy of the oriented nanochannel MOF structure and evaluate the diffusion selectivity for the isomers. Subsequently, we establish the dynamic chemical interactions in the MOF thin film and apply those to reverse isomer diffusion selectivity.

The selected nanoporous system is a pillared-layer type MOF39 (Fig. 2a); a Cu2+-dimeric paddle-wheel node is linked by bdc (1,4-benzenedicarboxylic acid) to form a square-grid type 2D layer. This 2D layer is pillared (along [001] axis) by an azbpy (4,4’-azobipyridyl) to form a PCU topology Cu(bdc)(azbpy) MOF having two distinct pore windows. The window dimensions are 7.3 Å × 4.3 Å (along [001]) and 9.7 Å × 6.9 Å, calculated by adding van der Waals surface in a periodic density functional theory (DFT) optimized structure (at 0 K). To realize the MOF pore window orientation, as illustrated in Fig. 2a, we have used a layer-by-layer, liquid-phase epitaxial growth technique40,41. A self-assembled monolayer (-OH terminated) functionalized Au surface was alternately exposed to Cu(CH3COO)2 and mixture of bdc and azbpy linkers solution to grow the surface anchored MOF or SURMOF (described elsewhere)39. Out-of-plane x-ray diffraction (XRD) pattern exhibited diffraction peaks related to (001) plane, and in-plane pattern exhibited diffraction peaks related to (100) and (010) planes (Fig. 2b). This confirmed a [001] oriented SURMOF, as illustrated in Fig. 2a (crystallographic preferred orientation42 ((002)/(010) ~ 120; see supplementary information). The scanning electron microscopy images confirmed a monolithic film growth, as illustrated in Fig. 2c. Note that the pore window dimensions are large enough to allow diffusion of the bromopropane isomers (1BP = 8 Å × 4.7 Å; 2BP = 6.9 Å × 6.6 Å, calculated by adding van der Waals surface). For the [001] oriented SURMOF, the Cu(bdc) planes are exposed to the surface. Hence, we anticipated that the geometry based adsorption and diffusion selectivity for the bromopropane isomers will be regulated by the 7.3 Å × 4.3 Å sized pore window.

Fig. 2: Diffusion selectivity in oriented nanochannel.
figure 2

a Surface grown oriented structure of Cu(bdc)(azbpy), optimized at 0 K, orange = Cu, gray = C, red = O, blue = N; (b) simulated (black), out (red) and in-plane (blue) XRD patterns of the Cu(bdc)(azbpy), (c) 1BP and 2BP vapor uptake profiles at 298 K; black line is the fitting; inset: SEM image of Cu(bdc)(azbpy) thin film.

Full size image

To measure the adsorption and diffusion selectivities, we have used quartz crystal microbalance (QCM) technique39,43. In this method, SURMOF is grown on Au-coated quartz crystal sensor and mounted inside a fluidic cell. A constant flow of saturated solvent vapor through the fluidic cell allow measuring the mass uptake (mass is calculated using Sauerbrey equation, see experimental section). For the Cu(bdc)(azbpy) thin film, the mass uptake profiles for the isomers are shown in Fig. 2c and Supplementary Fig. 1. We describe the uptake profiles using an exponential decay function44:

$${M}_{t}={M}_{{sat}}(1-{e}^{-\frac{t}{\tau }})$$

\(\tau \,({time\; constant})=\frac{{l}^{2}}{3D}\) in the absence of surface barrier39 effect. Here, \({M}_{t}\) = adsorbed molecules/ pore; \({M}_{{sat}}\) = adsorbed molecules/pore at saturation; t = time in second, l = film thickness in meter and D = diffusion m2/s. Using this fitting function, the estimated diffusivity for 2BP is found to be ~3 x larger than 1BP (Fig. 2c; D of 1BP and 2BP are 0.47 × 10−15 and 1.35 × 10−15 m2/s). However, the adsorption amounts at saturation are ~1 and 0.8 molecule/pore for 1BP and 2BP, respectively. The adsorption selectivity of ~1.25 for 1BP is not surprising, as many of the MOFs45,46,47,48,49,50 and other porous materials38,51 exhibit similar type of selectivity for linear alkanes over branched isomers, mainly due to the higher contact surface area of linear alkanes.

One possible explanation of this opposing trend of adsorption and diffusion is following: higher adsorption is due to stronger adsorbate-adsorbent interaction, which reduces the molecular mobility52. To appraise this observation, MD simulation was performed on the most probable conformation obtained from AIMD simulation of the periodic unit of Cu(bdc)(azbpy) at 300 K (see supplementary information). At first we have excluded framework dynamics, because we anticipated only adsorbent-adsorbate interaction-driven diffusivity trends. As illustrated in Fig. 3a and Supplementary Fig. 2, the diffusion selectivity along [001] axis was found to be 1BP > 2BP (estimated from mean square displacement, MSD, See Supplementary Table 1). This is in contrary to the experimental observation and also implies that only adsorbate-adsorbent interaction strength is not the governing factor. In the next step, we have introduced framework dynamics and performed a similar simulation as done for rigid framework. Comparison of the MSD profiles indicated a selectivity trend of 2BP > 1BP, in accordance to the experimental data. Assessment of the effective close proximity interactions (g(r)) between isomers and host framework revealed that the most influential chemical group in the framework is the bdc (Supplementary Fig. 3). The faster diffusion of 2BP in comparison to 1BP can be rationalized based on following order of interactions: 2BP – bdc > 1BP – bdc, 1BP – azbpy > 2BP – azbpy. Analysis of the specific Br – MOF interactions reveals that there is a stronger specific Br – bdc i.e. Br– π interaction for 2BP than 1BP (Fig. 3b and Supplementary Fig. 4). The specific Br – π(bdc) interaction is further validated by performing ab initio MD (AIMD) simulation and analyzing the trajectory during the timespan of intrapore molecular movement (see experimental section, Fig. 3c; note that the diffusion selectivity observed in this simulation is same as the one observed in MD of flexible MOF, see Supplementary Fig. 5a). Stronger interaction with bdc accelerates diffusion, while stronger interaction with the azbpy decelerates diffusion. These observations underscore that in addition to the chemical interactions, the framework dynamics also contribute to the overall driving force (supplementary information movie 1 illustrates the framework dynamics during diffusion). We term this effect as “dynamic chemical interaction”, a phenomenon validated in subsequent sections.

Fig. 3: Framework dynamics and diffusion control.
figure 3

a Overview of the 1BP vs 2BP selectivities observed for rigid, flexible and in silico designed MOFs along [001] direction, using MSD from MD simulations, the scale bars are relative, trend of the selectivity showing the effect of flexibility and chemical functionality, the arrow indicates x-axis related to the MSD values; (b) a snapshot of the MD simulation during the intrapore passage of the 2BP molecule in the flexible Cu(bdc)(Azbpy), green sphere indicates Br of 2BP; (c) the probability distribution for Br···C (of bdc) distance for 1BP and 2BP obtained from AIMD simulation; inset: a snapshot of the AIMD simulation during the intrapore passage of the 2BP molecule in the flexible Cu(bdc)(Azbpy), pink sphere indicates center of mass of 2BP. orange = Cu, gray = C, red = O, blue = N.

Full size image

Drawing from the MD simulation insights, we have in silico reconfigured the pore windows along [001] orientation; i.e. substituting the bdc linker with a Br2-bdc (2,5-dibromobenzene-1,4-dicarboxylic acid) linker. This intuitive chemical functionality transformation changes not only the specific chemical interactions between the chemical isomer and the bdc linkers but also changes the framework dynamics. The change in the framework dynamics of the bdc linkers is also captured in the most probable configuration obtained during AIMD simulation of the Cu(bdc)(azbpy) and Cu(Br2-bdc)(azbpy) at 300 K (Supplementary Fig. 5). We have performed a similar set of MD simulation for Cu(Br2-bdc)(azbpy), as done for Cu(bdc)(azbpy) (vide supra). As evident from the Fig. 3a and Supplementary Fig. 6, the MSD values obtained appear very different, than those observed for Cu(bdc)(azbpy). Mainly, 1BP diffusion is found to be relatively faster. Inspection of the close proximity interactions revealed following order: 1BP – Br2-bdc > 2BP – Br2-bdc and 1BP – azbpy <2BP – azbpy (Supplementary Figs. 7–8). This reverse order of interactions reverses the diffusion selectivity. We attribute this reversal to the proposed dynamic chemical interaction, as the diffusion is effected by chemical interaction and framework dynamics.

Next, we have experimentally attempted to execute the in silico findings. Attempts to synthesize an isostructural, oriented Cu(Br2-bdc)(azbpy) thin film akin to Cu(bdc)(azbpy) proved unsuccessful (Supplementary Fig. 9). However, a successful strategy emerged through a mixed-linker approach21,53,54,55,56, yielding Cu(Br2-bdc)x(bdc)1-x(azbpy) (x = 0.012, 0.026 and 0.058) thin films (x was quantified by reverse-phase HPLC, see Supplementary Fig. 10). These mixed-linker MOF thin films maintained high crystallinity, preferred [001] orientation (crystallographic preferred orientation ~57, 55 and 648 for x = 0.012, 0.026 and 0.058, respectively, see supplementary information) and exhibited homogenous surface coverage, as evidenced by the out-of-plane XRD, SEM images, XPS elemental analysis and EDS mapping (Fig. 4a–c and Supplementary Figs. 11–14). Subsequently, we conducted 1BP and 2BP vapor uptake experiments using QCM for these mixed-linker MOF thin films (Supplementary Fig. 15). Note that we have verified the effect of surface barriers in the mixed-linker structure by performing a thin film thickness dependent mass uptake measurement. For the Cu(Br2-bdc)0.058(bdc)0.942(azbpy) thin film, the coinciding plots of fractional 1BP vapor uptake versus time confirmed that surface barrier effect is negligible in the mixed-linker MOFs (Supplementary Fig. 16). Similar to the case of Cu(bdc)(azbpy), we have calculated the saturation adsorption amount/pore and D. The Br2-bdc % vs D and adsorption amount/pore plots are presented in Fig. 4d, e. Across all the mixed-linker thin films, the saturation adsorption amounts are higher for 1BP, resembling the trend observed in the parent structure Cu(bdc)(azbpy). Moreover, with increasing % of the Br2-bdc, adsorption amount decreased for both the isomers. This reduction in adsorption can be attributed to the steric effect introduced by the bulky –Br atoms. A reversal in D is observed for Cu(Br2-bdc)0.058(bdc)0.942(azbpy) thin film. In comparison to the parent structure, D value for 2BP decreased ca. 8x and for 1BP increased ca. 0.5x.

Fig. 4: Reversal of diffusion selectivity.
figure 4

a A schematic of oriented mixed-linker MOF, ball and stick model; orange = Cu, gray = C, red = O, blue = N and green = Br; b out-of-plane XRD patterns of the Cu(bdc)(azbpy) and Cu(Br2-bdc)x(bdc)1-x(azbpy), x = 0 (black), 0.012 (red), 0.026 (blue) and 0.058 (green); c left to right: SEM morphology (scale bar = 1 μm), Br and Cu elemental mapping of Cu(Br2-bdc)0.058(bdc)0.942(azbpy) thin film, color gradient scaled to atomic %; d D for 1 and 2BP with varying % of Br2-bdc; e adsorbed molecules/pore for 1 and 2BP with varying % of Br2-bdc, the orange shaded regions indicate a crystalline phase, different than parent structure Cu(bdc)(azbpy). Error bars are calculated by considering the thickness variations in the thin film.

Full size image

The experimental observation may be correlated to the in silico experiment; however several other factors merit consideration: (i) inhomogeneous mixing of the linkers leading to segregated crystalline phases, (ii) the presence of structural defects, and (iii) changes in crystalline domain sizes. These three factors are discounted based on the following experimental observations: (a) Out-of-plane XRD patterns of the mixed-linker thin films did not reveal new diffraction peaks, confirming that a new crystalline phase of Cu + (Br2-bdc) +(azbpy) did not form. However, when the Br2-bdc % increased to 17, new diffraction peaks emerged (Supplementary Fig. 17). This confirmed that mixed-linker phase is feasible only for low % of Br2-bdc. (b) IRRA spectra of the mixed-linker and parent Cu(bdc)(azbpy) confirmed that the asymmetric and symmetric –COO stretching vibrations of the paddle-wheel node (1630 and 1388 cm−1, respectively) remained unaltered (Supplementary Fig. 18). This underscores the absence of new crystalline phase. In the case of 17% Br2-bdc, the asymmetric and symmetric –COO stretching vibrations are different than those of the mixed-linker MOFs, consistent with the out-of-plane XRD patterns (Supplementary Fig. 17). (c) Comparison of the (001) diffraction peak full width at half maxima for the mixed-linker and parent structure confirmed very similar crystalline domain sizes (30–34 nm) (Supplementary Fig. 19). (d) SEM images and elemental mapping of the mixed-linker film confirmed the homogenous coverage and uniform distribution of the Br2-bdc functionality (Fig. 4c). (e) Energy dispersive x-ray spectroscopy of Cu(Br2-bdc)x(bdc)1-x(azbpy) (x = 0.012 and 0.058) MOF thin films indicated that chemical composition (Cu, N, C, O) did not vary substantially in the different mixed-linker structure (Supplementary Fig. 20). (f) We have also observed the presence of Cu1+ in the high resolution XPS for all the thin films (in ~10 nm of thin film surface). A major fraction of Cu1+ originates due to x-ray exposure during analysis and sample activation (removal of solvents) by heating. We have verified the influence of Cu1+ in the observed diffusivity trend. A Cu2+/Cu1+ ratio vs diffusivity and adsorption plot is shown in Supplementary Fig. 21b, c. It is evident that Cu1+ abundancy is highest in case of x = 0.012, while lowest in x = 0, but this Cu1+ % change did not reverse the diffusion selectivity. Diffusivity is reversed at x = 0.058, and the Cu2+/Cu1+ ratio for this thin film is ~1, very similar (~0.73) to the thin film of x = 0.012. Also note that adsorption selectivities of 1BP/2BP are very similar for Cu2+/Cu1+ ratio of 2.5 and 1 (Supplementary Fig. 21c). Hence, Cu1+ did not influence the adsorption selectivity. These observations conclude that Cu2+/Cu1+ ratio does not control the selectivity. Based on all of these above mentioned observations, the reversed selectivity can be attributed to the chemical interactions which are observed for the in silico designed Cu(Br2-bdc)(azbpy). Note that a higher concentration of Br2-bdc in the Cu(bdc)(azbpy) may have more prominent effect on the diffusivity (i.e. selectivity); however those structures could not be realized experimentally.

Discussion

The chosen pillared-layer type MOF thin film exhibits distinct pore windows and functionality along the concentration gradient (i.e. [001]). Using these oriented nanochannels, we have concluded that diffusivity of two chemical isomers (1BP and 2BP) can be precisely manipulated and reversed using chemical design principles. To arrive at this conclusion, we have compared the observed chemical isomer diffusivities within a pillared-layer MOF thin film with those obtained from MD simulation. It is evident that diffusion has an intriguing dependence on the framework dynamics, while specific chemical interactions (like Br-π interaction) are also substantially important. We have hypothesized that the framework dynamics and chemical interactions as tool to predictively alter the chemical isomer diffusivity. Initially in silico and later by using a mixed-linker approach we have shown that diffusivity of isomers can be reversed. To ensure that the experimental findings are exclusively attributed to the dynamic chemical interaction, we have performed careful characterizations of the thin films. Although this predictive alteration of diffusion is currently showcased for a pair of haloalkane isomer within pillared-layer type MOF, it’s important to note that the chemical design route transcends the boundaries of specific isomers and porous materials. In the future, the proposed methodology will be implemented to develop membranes for improved separation efficiency of the chemical isomers which are more challenging to perform using conventional distillation and adsorption-based technique.

Methods

Synthesis of 4,4’-Azobipyridine

4,4’-azobipyridine was synthesized following a reported method57.

Synthesis of pillared-layer MOF thin films on QCM sensor

5 MHz (Au coated) QCM-sensors were dipped in an ethanolic solution (20 mM) of 11-mercapto-1-undecanol (MUD) for 24 h to obtain –OH functionalized surface. These substrates were then thoroughly washed with absolute ethanol (99.99%), dried and used for thin films synthesis. The MOF thin films were prepared on those functionalized substrate via a well-known layer-by-layer (lbl) liquid-phase epitaxial (LPE) method58. The method consists of four steps to complete a cycle at 60 °C as: i) dipped in 1 mM copper acetate ethanol solution for 15 min, ii) drained the metal solution and washed with fresh ethanol, iii) dipped in 0.2 mM linker solution (mixture of two linkers) in ethanol for 30 min and iv) drained the linker solution and washed with fresh ethanol. MOF thin films with varying doping percentage were prepared by varying the linker solution in different Br2bdc proportions. 4,4’-azobipyridine is the only pillar linker used with either 1,4-benzene dicarboxylic acid linker or mixture of two dicarboxylic acids (1,4-benzene dicarboxylic acid and 2,5-dibromobenzene-1,4-dicarboxylic acid) for MOF thin films upto 60 cycles.

Characterizations

Powder x-ray diffractometer (XRD) patterns of thin films were recorded on a Rigaku XDS 2000 diffractometer using nickel-filtered Cu Kα radiation (λ = 1.5418 Å) ranging from 5–20 ° at room temperature (voltage 40 kV, current 200 mA). Out-of plane PXRD was recorded in 2θ/θ (step size 0.01, scan rate 0.2 °/s), in-plane in 2θ/φ geometry with grazing incident angle (ω) at 0.5 ° and step size of 0.12 with scan rate 0.1 °/s.

Surface morphology of the MOF thin films were characterized using field emission scanning electron microscopy (FESEM), JEOL JSM-7200F instrument with a cold emission gun operating at 5 kV. Energy-Dispersive X-ray spectroscopy (EDS) elemental analysis and mapping were also done on the FESEM (at 15 kV).

IRRA (Infrared Reflection Absorption) spectrum (4000–600 cm–1) was collected under vacuum using Bruker VERTEX 70 v with 2 cm−1 resolution and with 128 scan rate.

X-ray photoelectron spectroscopy (PHI versaProbe III) was performed for the MOF thin films under ultrahigh vacuum (10−9 bar) environment.

The adsorption (mass uptake) profiles were measured using a quartz crystal microbalance (QCM) from open QCM, Italy.

Thickness for all the thin films was calculated using J.A. Wollam ellipsometer (alpha-SE). The data was fitted using a B-Spline model including surface roughness. The film thickness values for Cu(Br2-bdc)x(bdc)1-x(azbpy) (X = 0, 0.012, 0.026, 0.058 and 0.170) are 505 ( ± 98), 411 ( ± 28), 396 ( ± 4), 331 ( ± 54) and 431 ( ± 68) nm, respectively.

Analytical reverse-phase HPLC was performed on an Agilent HPLC instrument using an Agilent zorbax SB-C3 (5 μm), 4.6 × 150 mm reverse-phase column at a flow rate of 0.9 mL/min using a linear gradient of solvent B in solvent A at 40 °C (solvent A = 0.1% trifluoroacetic acid (TFA) in H2O; solvent B = 0.08% TFA in acetonitrile). The 214 nm UV absorbance of the column eluent was monitored. During sample preparation, compounds were weighed out in their mentioned ratios and dissolved in 200 µL of DMSO. From this stock solution, 5 µL was taken and diluted with 60 µL DMSO and 60 µL of B solvent (B = 0.08% TFA in acetonitrile). Then 0.5 µL was injected in HPLC for analysis.

MOF thin films deposited on QCM substrate were dipped in 18 mM aqueous solution of Na2EDTA·2H2O (Na2EDTA = ethylenediaminetetraacetic acid disodium salt) to disintegrate the MOF structure and remove Cu2+ from the solution. After pH adjustment to ~6, the clear aqueous solution (obtained by centrifugation) was taken for the HPLC analysis.

QCM experiments

MOF thin films were activated at 65 °C at 0.1 mbar. Mass uptake experiments were carried out using a constant flow rate (50 sccm) of dry N2, passing through saturated solvent vapors (1 and 2BP).

Analyses of uptake kinetics

Mass-frequency relationship for the QCM measurements is given by Sauerbrey equation 43;

$$\varDelta m=-c\frac{\varDelta f}{n}$$
(1)

Where n denotes the overtone order (n = 3, 5, and 7) and c is the mass sensitivity constant. For a 5 MHz crystal, c has value of 17.7 ng/cm2.

We examine the data with the assumption of Fickian diffusion, that is, we assume a constant diffusivity, D, is independent of the vapor concentration.

$$\frac{{M}_{t}}{{M}_{sat}}=1-\frac{8}{{{{\rm{\pi }}}}^{2}}{\sum }_{{{\rm{m}}}=0}^{\infty }\frac{1}{{(2{{\rm{m}}}+1)}^{2}}\exp \left(-\frac{4{{{\rm{D}}}{{\rm{\pi }}}}^{2}{{\rm{t}}}{(2{{\rm{m}}}+1)}^{2}}{{{{\rm{l}}}}^{2}}\right)$$
(2)

Where Mt is the uptake (g) at time t, Msat is the uptake (g) at infinite time (i.e., at equilibrium), D has units of m2/s, and l is the film thickness. Following the Wöll and coworkers report44, the above equation can be expressed as following:

$${M}_{t}={M}_{sat}(1-{e}^{-\frac{t}{\tau }})$$
(3)

Where \(\tau\) is a time constant and expressed as:

$$\tau=\frac{{l}^{2}}{3D}+\frac{l}{\alpha }$$
(4)

α is the surface permeability. In this case we neglect \(\frac{l}{\alpha }\) because surface barrier effect is not dominant. This is due to layer-by-layer synthesis methodology of the thin films 39.

D is calculated using the τ value, obtained by fitting Eq. 3. Note that the deviation in the fitting can be attributed to the following factors: a) D changes during the mass uptake; b) the experimental conditions require a strictly maintained vapor pressure and flow to achieve an exponential uptake profile, and this is challenging to strictly achieve; c) during mass uptake, frequency dissipation affects the applicability of Sauerbrey equation. Although the dissipation changes are small enough to neglect, mass calculation and hence rate of mass uptake can deviate from the ideal exponential function. Hence, to obtain better fitting, at lower mass uptake region following linear equation can be used:

$$\frac{{{{{\rm{M}}}}_{{{\rm{t}}}}({{\rm{t}}}})}{{{{\rm{M}}}}_{{{\rm{sat}}}}}\approx \frac{8}{\sqrt {{\pi }}} {\sqrt{\frac{Dt}{{L}^{2}}}}$$
(5)

Using Eq. 5, the fitting does not deviate (See Fig. 1b). The obtained ratio of the D for 1BP and 2BP uptake in Cu(bdc(azbpy) is ~3, close to the value (~2.8) obtained by using Eq. 3 fitting (See Supplementary Fig. 1b)43.

Note that the QCM vapor uptake measurements are carried out under a constant flow of vapors. During the measurements, constant flow maintenance and minimum dissipation change are necessary to achieve an uptake profile, which can be satisfactorily fitted using Eq. 3.

Molecular dynamics simulation

At first, the corresponding superstructure is generated from the unit cell of the Cu(bdc)(azbpy) MOF spanning along 3  * 3 * 6 dimensions. We have considered two situations with the superstructure framework extended as 3 * 3 * 6 (in x, y, z directions respectively) considering: (I) high concentration gradient, i.e MOF thin film pores are almost empty (containing only one molecule of each of the alkanes, 1BP and 2BP in the framework), (II) low concentration gradient, i.e. ~20% (of saturation amount) filled pores (including multiple molecules of each type of alkane at a time, i.e. 11 molecules of 1BP and 9 molecules of 2BP corresponding to the respective number of molecular uptakes at ~20% loading). Initially, in both the cases molecular dynamics simulation is performed by freezing the MOF (utilizing ‘freeze group’ utility installed in gromacs) as we anticipated only adsorbent-adsorbate interaction driven diffusivity trends. The partial charges over the atoms of MOF are obtained from the quantum calculations (see below) and the alkane molecules are modeled using charmm36 force field parameters59,60,61. Each of the simulation both in high and low concentration gradient for each of the haloalkane molecules are performed in gas phase. The entire system was packed in a rectangular box of dimension 3.26 × 3.26 × 9.54 nm3 as per the resultant dimension of the superstructure.

Further, the similar set of simulations was performed in flexible framework. The respective bond, angle and dihedral parameters of the MOF were obtained using obgmx tool and the partial charges were kept unaltered as the set of the previous simulations performed excluding framework dynamics were excluded.

To realize the effect of bromine substitution in MOF on the haloalkane isomer selectivity, Cu(Br2-bdc)(azbpy) has been simulated under the condition of high concentration gradient, i.e MOF thin film pores are almost empty (containing only one molecule of each of the alkanes, 1BP and 2BP in the framework). The simulations in brominated MOF for each of the haloalkane were carried out in flexible framework arrangement where the partial charges of MOF were obtained from the similar quantum calculation (see below) and the bond, angle and dihedrals parameters from obgmx. The alkanes were modeled with charmm36 parameters as utilized before. The dimension of the simulation box was kept fixed corresponding to the similar dimension of the MOF superstructure build along the direction of 3 * 3 * 6 (corresponding to x, y and z directions respectively).

Simulation method: Each of the simulation is performed using periodic boundary conditions (PBC) set in all three dimensions. Long-range electrostatic interactions were maintained employing the particle mesh Ewald (PME) method62 with cubic interpolation. For the electrostatic interactions at short-range, the cut-off of 1.2 nm was employed. During freezed framework simulation of the Cu(bdc)(azbpy), the MOF dynamics was excluded using “ freeze group” utility of gromacs. Otherwise for the alkane molecules in the freezed system and the MOF along with alkanes in the flexible framework system, for constraining each the bonds involving hydrogen atoms, the LINCS algorithm63 was applied. At first, the system was energy minimized with the steepest-decent algorithm followed by stepwise equilibration in seven successive steps with gradual increase of temperature (in an interval of 50 K starting from 50 K upto 300 K) of 100 ps each (with time step of 0.0005 ps). During equilibration, the average temperature was kept fixed at the corresponding temperatures by using V-rescale thermostat via coupling the MOF and the alkane molecules separately. Finally, the equilibrated system was subjected to NVT production run for 10 nanosecond. During production simulation also, the average temperature of 300 K was maintained with the help of same V-rescale thermostat. To execute all simulations GROMACS software of version 20 x were utilized. To attain statistical reproducibility, each of the simulations is repeated multiple times.

The diffusion phenomenon of the haloalkane molecules were inspected by calculating mean square displacement (msd) utilizing the tool of “gmx msd” and the corresponding diffusion coefficient (D) were approximated. To understand the mode of chemical interactions of the haloalkane molecules with the different parts of the MOF pair correlation function of the alkane moieties (whole molecule, bromine atom and the Cα carbon of the alkane molecule linked to the bromine group) were measured with respect to the specific parts of the MOF (i.e. –N = N-, pyridyl and bdc). The event of molecular diffusion (2BP) into the flexible Cu(bdc)(azbpy) is shown in supplementary video 1. It is evident that during pore-to-pore movement of 2BP, linker orientation (by rotation) changes much faster than the movement of 2BP molecule. Hence a specific orientation of the linker cannot explain the diffusivity; rather a dynamic interaction is the key.

Ab initio molecular dynamic simulation

All AIMD simulations were run using CP2K software64 (version 9.1) with PBE functional65 and each MD time step of 0.5 fs at 300 K. The dimensions of the cell with periodic boundary conditions were 10.886 Å, 10.886 Å, and 15.9041 Å. The valence electrons of H, C, N, and O atoms were modeled with DZVP-GTH basis sets whereas DZVP-MOLOPT-SR-GTH basis set was employed for Br and Cu centers. The core electrons of all the atoms were modeled using GTH-PBE pseudopotentials. All NVT simulations employed Nose-Hoover chain thermostatting66,67,68. For the self-diffusion studies, NVT simulations were run for 50 ps. The analysis of the probability distribution of Br (2BP and 1BP) - C (bdc linker) distance involved data collected at an interval of 5 fs during the crossing of the molecule across the pore (1BP: 12.5 ps – 17.5 ps; 2BP: 25 ps – 29 ps) surrounded by the bdc molecules. The MSDs were computed with freud code69. The calculation of the diffusion constant was done by linear fitting of the MSD data (between 12.5-17.5 ps for 1BP and 22-28 ps for 2BP).