Introduction

Both lattice geometry and dimension could profoundly shape the electronic structures of materials. Lattices with unique geometric configurations, including the kagome lattice1,2, Lieb lattice3,4, etc, exhibit correlated electronic excitations characterized by quenched kinetic energy of carriers in the flat band. Notably, diverse correlated phases, such as the giant anomalous Hall effect5,6,7, quantum spin liquid8,9,10,11, charge density wave12,13,14,15, and unconventional superconductivity16,17,18, have been observed in bulk kagome metals. Nonetheless, introducing these lattice-borne correlated excitations to 2D semiconductors, essential for device applications due to enhanced Coulomb interaction and versatile carrier concentration tunability, remains challenging.

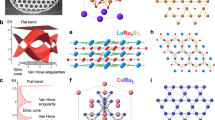
The kagome lattice, comprised of corner-sharing triangles (Fig. 1a), represents a prototypical model for generating flat bands or van Hove singularities (VHSs). However, experimental confirmation of kagome bands in 2D materials has been limited due to the instability of kagome configuration in two dimensions. Thus, alternatives such as the distorted kagome lattice (Fig. 1b) and the coloring-triangle (CT) lattice (Fig. 1c) have been proposed19,20 to exhibit a relatively rigid lattice and preserve the kagome bands. Both ways arise from rotating two sets of corner-sharing triangles within the kagome lattice. The CT lattice involves three types of hopping parameters, where t1 and t1’ are ideally identical, and t2 is zero. Its Hamiltonian is unitarily equivalent to that of the kagome lattice. Consequently, the band structures of the CT lattice also display a VHS, flat band and Dirac cone20,21, as demonstrated in Fig. 1d. Even with slightly increased nonvanishing t2, the key features remain, except when t2 becomes comparable to or exceeds t1 (t1’), leading to noticeable deviations from the archetypal kagome bands. The breaking of mirror symmetry (t1 ≠ t1’) as shown in Fig. 1e only makes the Dirac cone massive, while the VHS and flat band persist in the band structures.

Fig. 1: Illustration of the CT lattice band structures.
figure 1

a, b, c Schematic diagrams of the (a) kagome lattice, (b) distorted kagome lattice, and (c) CT lattice, which illustrate the evolution of the CT lattice from the unitary equivalent kagome lattice via rotating the corner-sharing triangles (θ). Three sets of hopping parameters, namely t1, t1’, and t2, are denoted by different colors. d Evolution of the CT lattice band structures with t1 = t1’, but the hopping parameter t2 tuned from t2 = 0 to t2 = 2 t1. e The CT lattice band structures that keep (blue, t1 = t1’) or break (red, t1 ≠ t1’) the mirror symmetry.

Full size image

Various material platforms have been proposed theoretically to achieve the CT lattice, such as Au patterned Ca2N20, monolayer B2S322, Cu-dicyanobenzene23, etc. However, none of these proposals have been materialized yet. Some experimental efforts have been paid to investigating the CT lattice in monolayer MoTe2 and bulk 1T-TaS224,25. Nonetheless, the complexity arises in these materials as each superlattice site consists of an atomic cluster containing several atoms, leading to intricate electronic structures. Hence, the development of 2D materials with atoms arranged on a CT lattice remains limited.

Herein, we report the molecular beam epitaxy (MBE) synthesis of semiconducting 2D Cr8Se12 with 7-atomic-layer thickness. Structural characterization shows that the atom-based CT lattice can be obtained by forming two atomic adlayers (Se-Cr) on the previously reported 5-atomic-layer Cr2Se3. Based on the scanning tunneling spectroscopy (STS) and angle-resolved photoemission spectroscopy (ARPES) investigations, a bandgap of about 0.80 eV and a VHS close to the VBM (Supplementary Fig. 10) are observed. The first-principles analysis reveals that the kagome-like bands residing in the CT lattice originate from the top-layer Se pz orbitals with alternative hopping parameters modulated by the underneath Cr honeycomb. The semiconducting nature and the divergent local density of states (LDOS) around the VBM render this material a promising candidate for investigating 2D strongly correlated physics in semiconducting devices.

Results

Crystal structures of 2D semiconducting Cr8Se12

The crystal structures of 2D chromium selenides including CrSe26, CrSe227,28, and Cr2Se328,29, are influenced by the synthesis methods and conditions. Here, the 2D chromium selenide was synthesized on graphite via MBE (see “Methods”, Supplementary Fig. 20 and Supplementary Fig. 22). A typical large-scale scanning tunneling microscopy (STM) topography of the as-grown chromium selenide is displayed in Fig. 2a, in which two types of terraces with different thicknesses are observable. The STM line profile (Fig. 2a, inset), taken along the orange dashed line, reveals the typical thicknesses of 1.03 nm and 1.30 nm, respectively. Based on detailed structure characterizations (Supplementary Note 1, Supplementary Fig. 1), we determined that the thinner phase with a lateral lattice constant |a0 | = 0.370 ± 0.003 nm is the previously reported “2D Cr2Se3”. This phase has a 5-atomic-layer thickness28 and is composed of alternating stacks of Se-full and Cr-full layers along the (001) direction.

Fig. 2: Crystal structure characterization of 2D Cr8Se12 on graphite.
figure 2

a STM topography (Vs = 2 V, I = 5 pA) of the chromium selenide sample with an orange dashed line across the 5-atomic-layer Cr2Se3 and 7-atomic-layer Cr8Se12. Inset: STM line profile along the orange dashed line. Scale bar: 15 nm. b LEED pattern of the as-grown chromium selenide sample on graphite. The black, red, and blue circles denote diffraction patterns from the graphite, 2D Cr2Se3, and 2D Cr8Se12, respectively. c, d STM (c) and nc-AFM (d) images of the interface region acquired at the same scanning window. The lattice of 2D Cr8Se12 (2D Cr2Se3) is represented by the blue (red) circles. The primitive lattice vectors of 2D Cr8Se12 (2D Cr2Se3) are denoted by a and b (a0 and b0), respectively. Imaging conditions for Fig. 2c: Vs = 1.6 V, I = 100 pA. Imaging conditions for the lower (upper) part of Fig. 2d: z0 = −200 pm (z1 = −470 pm = z0 −270 pm) relative to Vs = 0.3 V, I = 100 pA. Scale bars: 1.6 nm. e, f Atomic-resolved (e) constant height STM and (f) nc-AFM (Vs = −0.01 V, z = −340 pm relative to Vs = 0.3 V, I = 100 pA) images of 2D Cr8Se12 obtained within the same scanning window, with the unit cell marked by the white rhombus and with different interatomic distances (a1, a1’, and a2) by triangles with diverse colors. Scale bars: 0.6 nm. g Statistical analysis of the measured nearest-neighbor interatomic distances: a1 = 0.370 ± 0.005 nm, a1’ = 0.387 ± 0.007 nm and a2 = 0.355 ± 0.005 nm. The distances were determined from Gaussian curve fitting of the histograms, with errors representing the standard deviations. h Crystal structures of 2D Cr8Se12 along different axes with the unit cell marked.

Full size image

As for the thicker phase, structural analysis was conducted by examining the surface lattice arrangements of the two phases at the interface. Figure 2c, d present the STM and non-contact atomic force microscopy (nc-AFM) images obtained at the same scanning window, from which the surface lattice arrangements of thinner and thicker phases can be visualized simultaneously. Comparison of the surface Se triangle lattices of the thinner (upper) and thicker (lower) halves, represented by blue and red circles (Fig. 2d), reveals identical crystalline orientation and commensurate lattice constants between the two phases. The low energy electron diffraction (LEED) pattern in Fig. 2b, obtained from the sample incorporating both phases, exhibits only one set of diffraction spots aligned with graphite. All these above witness a step-flow growth relation between the two phases. Further cross-sectional scanning transmission electron microscopy characterization (Supplementary Fig. 3) also suggests that thicker phase is formed through continuous epitaxial growth of additional Cr and Se layers on the 2D Cr2Se3, resulting in a 7-atomic-layer crystal structure.

The atomic-resolved STM and nc-AFM images of the 7-atomic-layer phase, obtained within the same scanning window, are presented in Fig. 2e, f, respectively. Unlike STM, which relies on tunneling current for atomic-resolved imaging, nc-AFM utilizes short-range forces, allowing for a more precise determination of the real positions of surface Se atoms. A discernible (√3 × √3)R30° surface reconstruction (depicted as the rhombuses in Fig. 2e and Supplementary Fig. 8) is easily identifiable. Statistical analysis indicates three distinct nearest-neighbor interatomic distances, denoted as a1, a1’, and a2, within the (√3 × √3)R30° unit cell (Fig 2f, g). Notably, the periodic lattice distortion shapes the CT lattice geometrically. Indeed, the STM image displayed in Fig. 2e also exhibits a kagome-like morphology, indicating the potential of the thicker 7-atomic-layer phase for investigating the electronic properties of the kagome lattice.

To explain the (√3 × √3)R30° surface reconstruction, we proposed three distinct crystal structures featuring 1/3, 2/3, and a full layer of Cr beneath the topmost Se (Supplementary Figs. 4a–c), corresponding to 1, 2, and 3 Cr atom(s) in the Cr adlayer per unit cell, respectively. Through density functional theory (DFT) calculations on their band structures (Supplementary Figs. 4d–f, Supplementary Fig. 5), we found that only the configuration with a 2/3-layer of Cr (Fig. 2h) exhibits a semiconducting behavior. Considering the experimentally determined semiconducting nature of the 7-atomic-layer phase (as discussed later), we identify the crystal structure as the one with a 2/3-layer of Cr beneath the topmost Se (Fig. 2h). Notably, the 2/3-layer Cr atoms form a honeycomb network, linking the surface CT-lattice distortion to this honeycomb Cr arrangement. Given that each unit cell comprises 8 Cr atoms and 12 Se atoms (Supplementary Fig. 16), we henceforth denote the 7-atomic-layer phase as 2D Cr8Se12.

The crystal structure was further definitively elucidated through an analysis of its electronic properties using ARPES and DFT calculations. Figure 3a illustrates the (√3 × √3)R30° commensurate relation between 2D Cr8Se12 and 2D Cr2Se3, which causes an overlap of high-symmetry points between their respective Brillouin zones (BZs). The ARPES valence band dispersion in both BZs reveals their semiconducting nature (Fig. 3b). This is further demonstrated by the Fermi surface mapping (Fig. 3c), where only the π bands from the graphite substrate are observable. To identify band contributions, band structures of both phases were calculated (Fig. 3b) considering a small fraction of 2D Cr2Se3 in the Cr8Se12 sample used for ARPES measurements (Supplementary Fig. 2c). The superimposition of these band structures on the ARPES spectra demonstrates the agreement between theoretical calculations and experimental observations, corroborating the proposed crystal structures.

Fig. 3: Electronic structures of 2D Cr8Se12 on graphite.
figure 3

a The geometric relation between the BZs of 2D Cr8Se12 (orange), 2D Cr2Se3 (blue), and the graphite substrate (black). b Second-derivative ARPES dispersion of the as-grown chromium selenide on graphite, which is measured at T = 40 K and displayed along the Γ-M1-K2 and Γ-K1-M2 directions as defined in Fig. 3a. The DFT band structure of 2D Cr2Se3 (blue, Supplementary Fig. 17) and unfolded band structure of 2D Cr8Se12 (orange, Supplementary Fig. 15) are superimposed for comparison with the ARPES data. The partial flat band near the M1 point is marked by a white dashed rectangle. c Constant energy contour at Fermi level. Scale bar: 0.5 nm−1. The Dirac cones of the graphite at Fermi level are marked by black arrows in Fig. 3c. d The schematic crystal structures of the topmost two atomic adlayers for cross comparison with Fig. 3f–k. Three types of triangles are marked by different colors. e Energetically aligned dI/dV spectrum acquired on 2D Cr8Se12. (Vs = 0.30 V, I = 100 pA, f = 963 Hz, Vr.m.s. = 10 mV, T = 4.3 K). f-h Constant-height dI/dV maps of 2D Cr8Se12 acquired at the same region and at energies corresponding to the (f) CBM (Vs = 20 mV), (g) VBM (Vs = −0.8 V), and (h) VHS (Vs = −1.1 V), respectively. i–k DFT simulated charge density distributions of 2D Cr8Se12 acquired at energies corresponding to the (f) CBM, (g) VBM, and (h) VHS, respectively. Three types of triangles are marked by different colors as in panel (d).

Full size image

Band structure assignment also facilitates the exclusion of 2D Cr2Se3 during the analysis of 2D Cr8Se12 by comparing ARPES with localized STS characterizations. Specifically, the VBM revealed in dI/dV spectrum (Fig. 3e) closely aligns with the ARPES (Fig. 3b, Supplementary Fig. 9 and Supplementary Fig. 18) VBM, except for a slight downward shift attributable to the photohole doping that typically happens in semiconductors30. A bandgap of ~0.8 eV is observable in dI/dV spectrum, which is consistent with the absence of ARPES conduction band minimum until the Fermi level. Additionally, the LDOS (Fig. 3e and Supplementary Fig. 14) also manifests a pronounced valence peak centered at Vs = -1.10 V, which is energetically aligned with a partial flat band near the M1 point (Fig. 3b), i.e., the M point of 2D Cr8Se12.

The electronic structures including the VHS can be visualized in real space through dI/dV mapping within a specific region as illustrated in Fig. 3d. The dI/dV maps in Fig. 3f-h were measured at energies corresponding to the conduction band minimum (CBM), the VBM, and the VHS, respectively, which were reproduced by the DFT simulated charge density distributions at the corresponding energies (Fig. 3i-k). Notably, the mapping at VHS shows an electron localization at the Cr-bridged Se atoms, resulting in a kagome-like CT lattice pattern. Nevertheless, the LDOS distribution at the VBM presents the hexagonal close-packed trimers, corresponding to the parabolic band dispersion at the Γ point.

CT lattice-derived kagome-like bands in 2D Cr8Se12

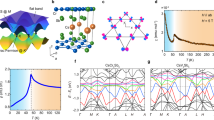
While VHS and kagome-like morphology have been observed in 2D Cr8Se12, their exact origins remain elusive. We started from a careful analysis on the band structures of 2D Cr8Se12 through orbital projection. Figure 4a illustrates the spin-polarized band structure projected onto the pz orbitals of the topmost Se atoms. Apparently, the energy states around the VBM, comprising six distinct energy bands, are primarily contributed by the topmost Se pz orbitals (Supplementary Fig. 11 and Supplementary Fig. 19). These six energy bands can be categorized into two sets based on their spins: three are spin-up, and the remaining three are spin-down. Notably, within each unit cell of 2D Cr8Se12, three topmost Se atoms lead to the observation of six energy bands arising from two sets of CT lattice energy bands with distinct spins. Consequently, the observed VHS contributed by the topmost Se pz orbitals is supposed to originate from the CT lattice.

Fig. 4: CT lattice in 2D Cr8Se12.
figure 4

a Spin-polarized DFT energy bands projected onto the top-layer Se pz orbitals. b Tight binding model of the CT lattice on 2D Cr8Se12 with the three types of hopping parameters denoted by t1, t1’, and t2. c Tight binding simulated energy bands showing qualitative agreement with the DFT band structure. d, e Side (d) and top (e) views of the charge density distribution at the energy corresponding to the VHS. In Fig. 4e, only the topmost two atomic adlayers and the upper lobes of the Se orbitals are displayed.

Full size image

The kagome-like bands can be further reproduced through tight binding simulations. Given the semiconducting nature of 2D Cr8Se12, we employed the tight binding approximation without considering electron correlation effects (See Supplementary Information Part 10, Supplementary Fig. 24, Supplementary Fig. 25 for a discussion on electron correlation effects). The tight binding Hamiltonian was constructed on a CT lattice (Fig. 4b) with two distinct sets of nearest-neighbor hopping parameters. As displayed in Fig. 4c, the simulated band structures demonstrate qualitative agreement with the DFT band structures (Fig. 4a), with minor discrepancies that can be attributed to the neglected next-nearest-neighbor hopping and orbital mixing effect (see Supplementary Information Part 8, Supplementary Fig. 11 and Supplementary Fig. 12 for details).

The CT lattice may stem from a triangular lattice with periodically altered hopping parameters, resulting in exotic electronic excitations (Supplementary Fig. 13 and Supplementary Fig. 23). As demonstrated in Fig. 3d, within each unit cell of 2D Cr8Se12, the topmost Se atoms constitute the distorted triangle sublattice, while Cr atoms are located only below two of the three Se triangles. Since the bridging of Cr atoms tends to enhance the nearest-neighbor hopping between the Se atoms, the hopping within the Se triangles connected by bridging Cr atoms would surpass those without bridging, and this hopping configuration (t1 ~ t1’ > t2) benefits the formation of the kagome-like band structure in 2D Cr8Se12.

The CT lattice characteristics observed in the STM image (Fig. 2e) and dI/dV map (Fig. 3f) can be explained at the atomic scale. Figure 4d displays a side view of the charge density distribution at the energy corresponding to the VHS, which not only verifies the major state contribution of the topmost Se pz orbital at this energy, but clearly reveals the periodic tilt of these pz orbitals. Thereafter, the Se pz orbitals, as surface states, contribute the primary intensity to both the ARPES measurement and dI/dV map. Figure 4e presents the top-view spatial arrangements of the topmost Se pz orbitals. By inspecting the tilt configurations, we found that the upper lobes of all the dumbbell-like pz orbitals tend to tilt toward neighboring Cr atoms. Consequently, the triangular configuration of pz orbitals contracts with the Cr in the middle, while expands in the absence of Cr at the center. This results in a prominent distortion of the triangular lattice and reproduces the observed dI/dV map with the CT lattice geometry. Additionally, the tilted orbitals at the atomic scale also substantiate the enhanced hopping t1(t1’) and the reduced hopping t2, thus resulting in the CT lattice-derived kagome-like bands.

Discussion

In summary, we have characterized the CT lattice in 2D Cr8Se12 with a 7-atomic-layer thickness, which is demonstrated to be a 2D semiconductor (See Supplementary Information part 4 and Supplementary Fig. 6 for discussion on the magnetic properties). The scalable synthesis of 2D Cr8Se12 not only expands the magnetic 2D materials family, but also opens a new avenue for investigating lattice-borne exotic electronic excitations. Notably, experimentally observed kagome-like bands originating from the CT lattice, accompanied by the prominently enhanced LDOS, were found near the VBM. This suggests a promising research direction involving the elevation of the VHS to the Fermi level, thereby enabling the observation of the proposed lattice-borne correlated phases.

Methods

Sample preparation

The 2D Cr2Se3 was grown in an ultra-high vacuum (UHV) MBE chamber with a base pressure of 1 × 10−10 mbar, which is connected to a commercial Omicron LT-STM/nc-AFM system. The cleaved single crystalline graphite (NGS Naturgraphit GmbH) or epitaxial graphene-terminated n-type 4H-SiC(0001) substrates have been used as the substrate. The graphite substrate was cleaved in air and immediately loaded into the MBE chamber to degas the surface contaminations. The epitaxial graphene was prepared by following the procedure demonstrated in ref. 31. High-purity Se (99.999%) and Cr (99.95%) were evaporated from a standard Knudson-style thermal effusion cell and an electron-beam evaporator, respectively, with a Se/Cr flux ratio higher than 10/1 and a substrate temperature of ~440 °C. The average growth rate for 2D Cr8Se12 is around 0.014 ML/minute.

STM/STS and nc-AFM measurements

For scanning probe microscopy characterizations, the as-grown Cr2Se3 samples were in-situ transferred into the Omicron LT-STM/nc-AFM system without breaking vacuum. The experiments were conducted at 4.3 K using a qPlus AFM sensor (spring constant k0 ≈ 1800 N⋅m−1, resonance frequency f0 ≈ 27.4 kHz, and quality factor Q ≈ 30,000) equipped with a tungsten tip. The clean and atomically sharp tip apex was obtained by applying repeated voltage pulses and controllable crashes on the Au(111) substrate, and the tip state was calibrated on the Au(111) surface before the STS characterization. The STS spectra and dI/dV maps were acquired using standard lock-in technique with a bias modulation of 10 mV at 963 Hz. All the dI/dV maps were collected in the constant height mode. An oscillation amplitude of 40 pm is used for all the nc-AFM imaging. The STM and nc-AFM images were processed using the WSxM software.

ARPES measurements

ARPES experiments were conducted in UHV conditions at 40 K with a SPECS PHOIBUS 150 electron energy analyzer and a helium discharge lamp (He Iα light, hν = 21.2 eV). To prevent surface contamination, the Cr2Se3 samples were capped with ~10 nm of Se by deposition of Se at room temperature before being transferred to the ARPES system. Before the ARPES characterization, as shown in Supplementary Fig. 21, the Se capping layer was subsequently removed by annealing the samples at 300 °C for 30 minutes in UHV conditions (2.5 × 10−10 mbar).

First-principles calculations

Our first-principles calculations were based on DFT as implemented in the Vienna Ab Initio Simulation Package using the projector augmented-wave method. The generalized gradient approximation with the Perdew−Burke−Ernzerhof realization was adopted for the exchange-correlation functional. The plane-wave cutoff energy was set to 500 eV. A Monkhorst Pack k-point mesh with a size of 11 × 11 × 1 was used for the BZ sampling. The crystal structure was optimized with the fixed experimental lattice constants and the fixed surface atom positions until the forces on the atoms were less than 0.001 eV/Å. To simulate the dI/dV maps, the partial charge density within an energy range of 0.02 eV centered at the specific energy was plotted as a function of the real space position.

Tight binding modeling

The spin polarized DFT analysis reveals that the major contributions to the six valence bands near the valence band maximum (VBM) are pz orbitals of the topmost Se atoms. Three of them are spin-up bands and the other three are spin-down bands. In the absence of spin-orbit coupling, the spin and orbital parts of the electronic wave function are decoupled. Therefore, the spin polarized electrons in each spin channel can be treated separately like for spinless particles. We describe this behavior within a single-orbital tight binding model of connected pz orbitals with two sets of hopping parameters, each of which corresponds to a set of spin-bands. By making a fit to the DFT spectra, we can determine the on-site energy \({\varepsilon }_{i}\) and the hopping parameters \({t}_{{\mbox{i}}}\). With these parameters, we solve the generalized eigenvalue equation \(H|\psi \rangle=E|\psi \rangle\) to obtain the tight binding spectra, where the spinless Hamiltonian is defined as \(H={\sum }_{{{{\rm{i}}}}}{\epsilon }_{i}{a}_{{{{\rm{i}}}}}^{{{\dagger}} }{a}_{{{{\rm{i}}}}}+{\sum }_{\langle {\mbox{i}},{\mbox{j}}\rangle }{t}_{{{{\rm{nn}}}}}({a}_{{{{\rm{i}}}}}^{{{\dagger}} }{a}_{{{{\rm{j}}}}}+{a}_{{{{\rm{i}}}}}{a}_{{{{\rm{j}}}}}^{{{\dagger}} })\). Here, \({t}_{{\mbox{nn}}}\) is the hopping parameter, which represents t1, t1’ or t2 as defined in Fig. 4b.