Introduction

With the recent advances in quantum technologies, various applications such as quantum computation and quantum communication1,2 are expected to be the next technological leap. Clock frequency or the speed of the quantum information processors is one of the most important factors determining the scalability and applications of the quantum technologies; if the generation or manipulation of quantum states is slow, the nonclassicality may dissipate due to the decoherence before any practical applications can be realized. The physical limit of the clock frequency is set by the carrier frequency of the physical system. Note that this carrier frequency does not directly translate to the clock frequency as the quantum information is usually encoded in frequency around the carrier frequency, i.e., the bandwidth of the system. Figure 1 visualizes this relationship. This is similar to how optical telecommunication or radio encodes classical information in the amplitude or frequency modulation, not at the carrier frequency, and the bandwidth of the modulation determines how fast information can be sent. In this regard, optical systems are one of the most promising platforms for building the utility-scale quantum processors as their carrier frequency is a few hundred THz, which allows high-speed state generation and measurements in principle. Moreover, by multiplexing their rich degrees of freedom, large-scale deterministic generations of various continuous-variable (CV) entanglement resources have been achieved3,4,5,6. These results form the basis for large-scale and high-speed optical quantum computation using optical CV systems.

Fig. 1: Relation between bandwidth and clock frequency.
figure 1

a Narrowband system. b Broadband system. f(t), the shape of the wave packet; x(t) temporal signal from the detector. The frequency bandwidth of the quantum light source limits the size Δt of the wave packet we can select. The bandwidth of the detector limits the sampling rate of x(t). This sampling rate has to be sufficiently high compared to the time scale of f(t).

Full size image

Despite the possibility, the current clock frequency of the optical quantum processors is far from THz. As almost every quantum applications can be broken down to state preparation, manipulation, and detection, we need to examine the bandwidth of these components to elucidate the limitations on the clock frequency. Among many factors, the bandwidth of squeezed light and homodyne detectors are the current main limiting factors. Regarding the former, the squeezed light is a ubiquitous resource for state generation and is typically generated from an optical parametric oscillator (OPO). The bandwidth of OPO, however, is usually ranged in MHz to GHz range. Recently, broadband optical parametric amplifier (OPA) has been developed and it has shown the frequency bandwidth on THz order7,8,9. Regarding the latter, the bandwidth of the homodyne measurement has been limited to a few hundreds of MHz10,11,12,13,14 due to the trade-off between the efficiency and the bandwidth of the photodiode in the photoelectric conversion of the optical signal15. This boundary has recently been pushed by using OPA as a phase sensitive amplifier (PSA) in the broadband measurement of squeezed light7,8,16,17,18; by preamplifying the optical quantum state to a strong classical signal that can tolerate optical loss, lossy but broadband homodyne detectors can be used. Using this approach, 43-GHz real-time homodyne measurement of single-mode squeezed light with PSA has been recently demonstrated18.

The squeezed light and the homodyne measurements can be grouped as Gaussian elements. In addition to these, we also need to prepare non-Gaussian states in the process of quantum computation19,20. Non-Gaussian states are usually generated with a probabilistic process called heralding method and generation rate is crucial. A prominent example is the generation of the logical qubit state such as Gottesman-Kitaev-Preskill (GKP) qubit21,22 for fault-tolerant quantum computation. It requires interference of multiple non-Gaussian states23,24,25,26,27 and although it has been recently demonstrated for a single-step interference28, multiple-step interference is essential in achieving GKP with required quality. Because the overall generation rate decreases exponentially with the interference steps, generation of optical GKP state is experimentally challenging.

Bandwidth of the system is a limiting factor of the generation rate3. As an example, if we have a continuous-wave squeezed light source with 100 MHz bandwidth and success probability of 1%, the generation rate will be 1 MHz. In the case of pulsed light, the generation rate is determined by the pulse repetition rate not the pulse width, so if we have 100-MHz-repetition-rate pulsed light and a setup with the same success probability, the success rate will be 1 MHz, regardless of the pulse width. We point out here that in the homodyne measurement using pulsed light, regardless of the pulse width, the optical signals are converted to the electrical signal with the frequency equal to repetition rate by interference with pulsed-light local oscillator. Thus, the bandwidth of the system works similarly in both systems. The recent generation of phase-sensitive quantum state with nonclassicality shows the generation rate on the order of 10 to 100 kHz with the bandwidth below 100 MHz10,11. There are also heralded generations of single-photon state with generation rate around hundred kHz13,14. Even if it is possible to increase the generation rate by polishing the performance of each component, eventually, the generation rate will be capped by the bandwidth of the system in both continuous-wave and pulsed systems. Therefore to increase the generation rate, fundamentally, we have to increase the bandwidth of the system.

In this paper, we demonstrate broadband generation and measurement for high-rate generation of non-Gaussian state via optical PSA. To demonstrate the versatility of our system, we perform full quantum-state tomography of the generated state and verify its quantum non-Gaussianity through the Wigner negativity. The tomography results show strong nonclassicality of the generated states. The full bandwidth of the state generation and measurement is 66 GHz, limited by electronics of our detection system. Many works aim to improve the generation rate by optimizing quantum circuits to increase the success probability. Meanwhile, our work contributes to rate improvements by offering a drop-in replacement to those setups, focusing on enhancing the bandwidth. Although our system can theoretically improve the rate by about 660 times, the bandwidth was limited down to 1 GHz due to the jitter of the photon detector used in this experiment. This results in the generation rate of about 0.9 MHz. Even then, both the bandwidth and the generation rate are roughly two orders of magnitude larger than the state-of-the-art phase-sensitive highly-pure non-Gaussian states in Ref. 10,11,12. Note that there are no limitations besides timing jitter (see Methods section) which can still be further improved by using photon detectors with smaller jitter29. As non-Gaussian states are indispensable for outperforming classical computation19, the key technology for broadband non-Gaussian state preparation established in this work opens a path to high-speed optical quantum applications. We believe that state preparation and measurement using PSA will become the next-generation optical quantum technology, replacing conventional squeezed light sources and homodyne detectors.

Results

Bandwidth and quantum state

Optical quantum state is described by the annihilation operator \(\hat{a}\) whose classical analog is the complex electric field. If we have a quantum state with the temporal mode f(t), the annihilation operator of this mode is \({\hat{a}}_{f}=\int\,{{\rm{d}}}t\,f(t)\hat{a}(t)\), where \(\hat{a}(t)\) is the time-dependent annihilation operator. We can also use Fourier transform to rewrite this in frequency domain as \({\hat{a}}_{f}=\int\,{{\rm{d}}}\omega \tilde{f}(\omega )\hat{\tilde{a}}(\omega )\), where \(\tilde{f}(\omega )\) is the Fourier transform of f(t) and \(\hat{\tilde{a}}(\omega )\) is the annihilation operator of single frequency mode ω (ω = 0 corresponds to carrier frequency). Thus, if we want f(t) to be narrow so that the clock frequency is high, our light source and the detector have to be sufficiently broad to correctly generate and measure all frequency component of \(\tilde{f}(\omega )\). The requirement of the broadband light source and the homodyne measurement for quantum state in temporal wave packet is visualized in Fig. 1.

Although \(\hat{a}\) can be used to describe the state, the actual observable that is measured is the quadrature operators \(\hat{x}\) and \(\hat{p}\) satisfying \([\hat{x},\hat{p}]=i\) (ℏ = 1). We can write the quadrature of the mode f(t) as \({\hat{x}}_{f}=\int\,{{\rm{d}}}t\,f(t)\hat{x}(t)\), where \(\hat{x}(t)\) is the quadrature values at time t. Thus, for the homodyne detector to be able to measure correct \({\hat{x}}_{f}\), it must have sufficient bandwidth to extract the value of the varying \(\hat{x}(t)\) on at least the time scale faster than the width of f(t).

Working principle of an OPA as a PSA

In this section, we review the working principle of OPA as a PSA and how it can be used in homodyne tomography. An OPA uses the second-order nonlinear effect where if we have input beam (frequency ω) and pump beam (frequency 2ω), the parametric amplification occurs due to the interaction between these two signals. When we view an OPA as a PSA, the input–output relation of the OPA can be described as

$${\hat{x}}_{{{\rm{out}}}}=\sqrt{G}{\hat{x}}_{{{\rm{in}}}},$$
(1)
$${\hat{p}}_{{{\rm{out}}}}=\frac{1}{\sqrt{G}}{\hat{p}}_{{{\rm{in}}}},$$
(2)

where G is the gain of the OPA. This relationship is the same as the squeezing operation3, but the main difference is that as we are doing PSA to do the measurement, the value of G is expected to be very large, typically around 100 to 1000 (20 to 30 dB) or even more. In such situation, the distribution of quadrature \({\hat{x}}_{{{\rm{out}}}}\) will be spread out, making it insusceptible to noise and loss. On the other hand, the distribution of quadrature \({\hat{p}}_{{{\rm{out}}}}\) will be susceptible to such imperfections. Note that if we try to amplify both quadratures simultaneously, there will inevitably exist noises added to both quadratures which is fundamental due to quantum mechanics.

Although we amplify the x quadrature in the above example, any quadrature can be amplified. This can be selected by changing the relative phase between the input signal ω and the pump beam 2ω. The relative phase between the pump beam and the input signal can be defined because the pump frequencies is exactly twice of the signal frequency. After the amplification, we can use a broadband but lossy homodyne detector to measure the quadrature values. If the homodyne detector efficiency is η, we can show that after amplification, the effective efficiency ηeff becomes18

$${\eta }_{{{\rm{eff}}}}=\frac{1}{1+\frac{1-\eta }{G\eta }}.$$
(3)

As an example, if G = 1000 and η = 0.5, we have ηeff = 0.999. Thus, with sufficient gain G, we can correctly measure the quadrature with lossy homodyne detectors. At the homodyne detector, the measurement phase is selected by the local oscillator phase and this phase also has to be locked to the amplified quadrature.

Experimental setup

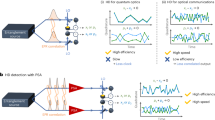
The non-Gaussian state is generated by tapping a portion of light from the squeezed light source and sending it to the superconducting nanostrip photon detector (SNSPD). This method is called photon subtraction30 and it is a basic method used to generate approximation of Schrödinger cat states10,31,32,33. Figure 2 shows the experimental setup. As a reference, we also show the setup of typical narrowband continuous-wave experimental setup for comparison in Fig. 2a. In narrowband experiment, the squeezed light is generated by the OPO and the bandwidth is limited by the linewidth of the cavity to be below GHz order. As the time scale in the narrowband experiment is much larger than the timing jitter of SNSPD, the effect of the timing jitter is negligible. The filtering cavity is used for selecting the resonant peak of the OPO to perform the photon subtraction as narrowband homodyne detector cannot detect the signals in all cavity modes. The frequency bandwidth of the herald path determines both the size of the wave packet and the generation rate. When the photon is detected, the next photon detection is unlikely to occur in that vicinity; we have to wait roughly the inverse of the frequency bandwidth to have a chance of detecting a photon again. Figure 2b shows the broadband setup used in this experiment. The state is generated and evaluated at the telecommunication wavelength at 1545 nm using continuous-wave laser. Instead of OPO, we are using OPA here which has the frequency bandwidth of 6 THz17, much broader than the narrowband experiment. There are two OPAs used in this experiments. The first OPA is used as a squeezed light source and the second OPA is used as a PSA. Because the timing jitter of the SNSPD used in this experiment is about 130 ps (see Methods section), we add an optical filter to limit the detection bandwidth to about 1 GHz to make the effects of the timing jitter negligible. After the preamplification with PSA, the generated non-Gaussian state is verified by commercially-available 70-GHz homodyne detector. PSA allows us to use a lossy broadband homodyne detector to measure the quadrature of the non-Gaussian state16,18. This is in contrast to homodyne detection in the typical setup which has bandwidth below hundreds of MHz due to the requirement of the quantum efficiency. See Methods section for the details of the experimental setup.

Fig. 2: Comparison between typical narrowband state generation system and broadband state generation system in this work.
figure 2

a Narrowband system based on optical parametric oscillator. b Broadband state generation and measurement based on optical parametric amplifier. OPO Optical parametric oscillator, LO Local oscillator, FC Filtering cavity, SNSPD Superconducting nanostrip photon detector, OPA Optical parametric amplifier, HD Homodyne detector, IBPF Interference bandpass filter, VBG Volume Bragg grating, FBG Fiber Bragg grating. See Methods for detailed parameters.

Full size image

Experimental results

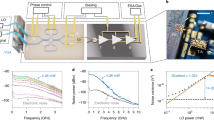
Figure 3 shows the temporal wave packet of the generated state and its Fourier transform. This wave packet is experimentally obtained by applying the principle component analysis on the quadrature values34. The wave packet has a bandwidth of 1 GHz with the shape that matches the prediction by the spectral property of the optical filter in the herald path (see Methods section). This wave packet is, to our knowledge, the most broadband among the non-Gaussian state generated and tomographed in CW regime. We vary the pump power of the squeezer OPA as 1 mW, 3 mW, 10 mW, and 25 mW. The generation rate for each pump power is 28 kHz, 88 kHz, 310 kHz, and 0.9 MHz, respectively. Compared to the highly-pure cat state generation with similar amplitude10, this is about two-order of magnitude higher.

Fig. 3: Wave packet of the experimentally generated state.
figure 3

a Temporal shape obtained from principle component analysis of the measured quadrature data. b Squared amplitude of the Fourier transform of the temporal wave packet.

Full size image

Figure 4 shows the tomography results for various initial squeezing levels. The quantum tomography is implemented using the maximum likelihood method35. We observe negative region of Wigner functions for all the pump power used here. The values of the Wigner function at the origin W(0, 0), i.e., the Wigner negativity, of each state are  −0.090 ± 0.004,  −0.097 ± 0.005,  −0.088 ± 0.005, and  −0.066 ± 0.006, respectively. Although the negativity is lower than the result in10, this is mainly due to the coupling efficiency to the measurement OPA which is currently about 90%. By improving the shaping of the spatial mode, this inefficiency can be reduced. The fidelity to the nearest ideal state is also calculated to be 0.64 ± 0.01, 0.65 ± 0.01. 0.63 ± 0.01, and 0.59 ± 0.01, to a squeezed single photon state of the squeezing level 0.5 dB, 0.7 dB, 1.4 dB, and 2.7 dB, respectively.

Fig. 4: Wigner function of the reconstructed states for various pump power.
figure 4

a 1 mW. b 3 mW. c 10 mW. d 25 mW. The insets are contour of the Wigner functions. No correction of inefficiency or optical loss is done in any steps for both raw data and maximum likelihood algorithm.

Full size image

To verify that the PSA allows us to correctly measure the non-Gaussian state, we also test the loss tolerance of the amplified signal. To do this, we add additional loss after the second OPA. Figure 5 shows the results. First, we observe in Fig. 5a that the negativity of the reconstructed states remained until about 15 dB loss. Even with 20 dB loss, although the negativity is no longer present, the non-Gaussian characteristic of the quadrature distribution is still apparent. This suggests that the quadrature values can be considered as classical values after the amplification using PSA. We also compare the fidelity of the reconstructed state when subjected to different loss after PSA. This is shown in Fig. 5b. We observe that the fidelity agrees well with the theoretical prediction and remains close to 1 for the loss up to 10 dB. Comparing to the theoretical predictions for the case without PSA, these results highlight the fact that optical preamplification using PSA allows us to correctly retrieve highly nonclassical quantum information.

Fig. 5: Effect of additional loss after PSA on state tomography.
figure 5

a Dependence of Wigner negativities on additional loss. b Dependence between the additional loss and the fidelity to state without additional loss. We also plot the theoretical prediction for the case where same additional loss is added, but we do not use the second OPA as an amplifier. The theoretical lines for the both with and without PSA cases are plotted using the experimental parameters of the setup. The insets in a show the quadrature distributions at antisqueezing phase for each loss. Although the dip near 0 becomes less resolvable with more loss, the non-Gaussian feature remains even with additional loss of 20 dB. The error bars show  ± 1 standard deviation.

Full size image

Discussion

State preparation, manipulation, and measurement are key components of quantum technologies. The bandwidth of these components limits the clock frequency of the system. In this work, we have utilized the broadband OPA to overcome the current technological limitation in both generation rate and measurement. The key point here is that OPA can be used as both squeezed-light source and PSA. Below we will discuss the current technological limitation and a possible solution to this.

The first limitation is the limitation related to the timing jitter of the photon detectors. The cutting-edge photon detectors have jitter below 3 ps29 that may allow us to improve the usable bandwidth of the current system (1 GHz). As the timing jitter of the photon detection system in this work is about 130 ps, we expect that this can improve the bandwidth of the system to tens of gigahertz. Even so, going beyond this into 100 GHz or even terahertz regime require different strategy. Technological-wise, low temperature detection and circuitry is the main bottleneck here. We envision two solutions. First solution is by using the timing jitter remover setup36. The second solution is by implementing room-temperature PNRD without using superconducting material. There is already a proposal for realizing this by using OPA as a PNRD37. This means that we can leverage the broadband room temperature circuitry. Moreover, this proposal allows the possibility of all-optical PNRD which is related to the second limitation that will be mentioned.

The second limitation is the speed of the homodyne readout. In this experiment, the quadrature is extracted by post-processing of the quadrature values obtained using 110-GHz oscilloscope with 256 GSa/s (see Methods section). Although we can remove this post-processing by using real-time measurement technique we have developed10, the wave packet size will eventually be limited by the bandwidth of the electronics. The most promising way to overcome this limitation is to remove all the electronics entirely and move to all-optical information processing. For a long time, it has been shown that as a PSA, OPA can also be used in the classical channel of the feedforward operation which will enable all-optical quantum teleportation38. Then, to achieve high clock frequency, we have to find the way to readout the THz bandwidth quantum information at the output of the quantum teleporter. Although this remains an open question, there is also an alternative suggestion of implementing multicore optical quantum computation instead of full tehahertz clock frequency18. We believe, however, that all-optical homodyne measurement read out should be possible and the key technology will again be the OPA. Therefore, OPA is the next generation device that will supersede various optical quantum technology and for high clock frequency quantum processors; OPA is all you need.

Methods

Detailed setup

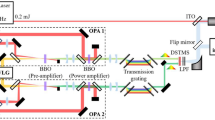
Figure 6 shows experimental setup. We generate Schrödinger cat states by using photon subtraction30. A portion of the squeezed states is tapped and photon detection on the tapped mode (herald mode) heralds generation of schrödinger cat state on the other mode. Continuous-wave (CW) laser operating at the wavelength of 1545 nm, and 772.5 nm generated from second harmonic generator (NKT Photonics) are used as light sources. We generate the squeezed light by pumping a PPLN-waveguide optical parametric amplifier (OPA) with 772.5-nm light17. The length of the waveguide is 45 mm, and the propagation loss is 8%. Frequency bandwidth of the squeezed states is over 6 THz. The squeezed light is tapped using a half-wave plate and a polarization beamsplitter, and the tapping ratio is 5%. In the herald path, we also add frequency filters consisting of interference filter (Alluxa, full-width half-maximum (FWHM): 130 GHz), volume-Bragg-grating (Optigrate, FWHM: 20 GHz), and fiber-Bragg-grating (TeraXion, FWHM: 1 GHz). Here, we need three filters because we are filtering out 1-GHz from 6-THz bandwidth of the squeezed light (see also the next paragraph) and a single filter does not provide adequate extinction ratio.

Fig. 6: Detailed experimental setup.
figure 6

AOM Acousto-optic modulator, EOM Electro-optic modulator, OPA Optical parametric amplifier, ISO Isolator, HD Homodyne detector, LO local oscillator, IBPF Interference bandpass filter, VBG Volume Bragg grating, FBG Fiber Bragg grating, SNSPD Superconducting nanostrip photon detector.

Full size image

After the tapped light passes through the herald filters, it is sent to photon detection. In this experiment, superconducting nanostrip photon detector (SNSPD) is used for photon detection. SNSPD operates at the temperature of 2.6 K and the detection efficiency is about 80%. Recently, it has been shown that timing jitter of the photon detection degrades the quality of output quantum state in the state preparation using heralding scheme36,39. The level of degradation level is mainly determined by product of the bandwidth of wavepacket and timing jitter. In our case, the overall jitter of photon-detection system is approximately 130 ps. Due to this, we limit the bandwidth of the wavepacket by setting the bandwidth of the herald filter to 1 GHz. We estimate the total efficiency of the herald system to be about 15%. Note that in the weak-pump limit, this efficiency only affects the event rates of the state preparation, but does not affect the quality of the output state.

The signal mode of the photon-subtracted state goes to the broadband homodyne measurement system. This system consists of a measurement OPA and a broadband telecommunication homodyne detector (HD). The coupling efficiency of the signal mode to the measurement OPA is 90%. The measurement OPA is pumped with 1-W pump beam (measured after OPA) which results in the amplification gain of 27 dB. After the signal mode passes through the measurement OPA and is amplified, it goes through a fiber isolator whose transmittance is 70%. Afterwards, the signal mode interferes with local oscillator (LO) light whose power is 45 mW measured in free space. The mode match between the signal mode and the LO light is measured to be 99.5%. After the interference, the lights are sent to the fiber-based broadband homodyne detector (HD) (Finisar, BPDV3120R). The electrical signal of the homodyne detector is further amplified by two electrical amplifiers (SHF, M827 B and M804 C) whose gains are 11 dB and 22 dB. The frequency bandwidth of each electrical component is as follows: HD, DC to 70 GHz; 11-dB amplifier, 70 kHz to 66 GHz; 22-dB amplifier, 90 kHz to 66 GHz; oscilloscope, DC to 113 GHz (Keysight, UXR1104A, 256 GSa/s); V connectors used for connecting components, DC to 66 GHz. As the bandwidth of the temporal mode is now limited to 1 GHz, we also add a lowpass filter with 5-GHz cutoff frequency to filter out signals and noise in the irrelevant frequency bandwidth. In principle, if there is no limitation due to SNSPD, this broadband HD setup can measure up to 66-GHz bandwidth quantum state in wavepacket.

To stabilize the experimental system, an auxiliary classical light called probe light is introduced in the setup. Because the probe light is much stronger than the quantum light, the control phase where the probe light is on and the measurement phase where the probe light is off are separated. Moreover, the optical path leading to the SNSPD is also closed during the control phase to prevent the probe light from saturating the SNSPD. Fiber AOMs are used for these optical switching. In this experiment, the switching cycle is 400 μs, of which 180 μs is the measurement phase.

Data acquisition and analysis

In the photon subtraction scheme at weak-pump limit, the temporal mode function f(t) of generated quantum states is described as

$$f(t)\propto \int\,d\tau C(t-\tau )g(-\tau ).$$
(4)

Here, C(t) is the time correlation function of initial squeezed state and g(t) is the total impulse response of herald system. Equation (4) shows that f(t) is a convoluation between C(t) and the time-reversal of the impulse reponse given by g( − t). In the current setup, as the frequency bandwidth of the OPA is much broader than the bandwidth of the herald filter, C(t) can be well approximated by a delta function and the temporal mode function becomes f(t) ≈ g( − t). The form of the g(t) in the current setup is mostly determined by FBG as its bandwidth is much narrower than the other components.

Although most experiments tend to assume that f(t) is a real function, f(t) can, in general, be a complex function. Measurement of quantum states with complex temporal mode function requires highly sophisticated system, making it unsuitable for actual quantum computation task40. In this experiment, we precisely adjust the temperature of the FBG so that the temporal response is a real function, i.e., the frequency spectrum is symmetric with respect to the carrier frequency. This adjustment has not been required in the narrowband cases as in those cases, the frequency filtering is done via optical cavity locked to the carrier frequency.

We evaluate generated quantum states with quantum tomography. We perform homodyne measurement in six measurement bases (0, 30, 60, 90, 120 and 150 degrees) and collect 5000 frames of data for each basis. For the current experiment, we rotate the phase of the initial state while keeping the phase of the PSA and LO locked. The temporal mode of the generated state is determined by applying principal component analysis3 to the acquired data. From the estimated temporal mode function, we calculate the quadrature amplitudes as

$${\hat{x}}_{f}=\int\,f(t)\hat{x}(t)dt,$$
(5)

where f(t) is the estimated mode function41 and x(t) is the temporal signals obtained from the homodyne detector. From the quadrature distributions, we use maximum likelihood method35 to reconstruct the density matrix with quantum tomography. The values of the Wigner negativity and fidelity shown in the main text are calculated from these density matrices, and their errors are evaluated using bootstrapping method42.