Introduction

Since their discovery, optical solitons1,2 have been the subject of intense study due to the rich physics underlying their dynamics3,4,5,6, relying on a delicate interplay of linear and nonlinear effects, as well as their broad application in areas including low-noise frequency synthesis7, astronomy8, and spectroscopy9,10, among others. Quadratic solitons11,12,13,14 can benefit from the inherent strength of the quadratic nonlinearity, which relaxes the requirement on resonator finesse or pump power for achieving soliton formation, as well as the ability to achieve efficient conversion between disparate spectral bands.

Temporal simultons are one such quadratic soliton, which consist of a co-propagating bright-dark soliton pair at the fundamental and second harmonic frequencies, respectively15,16. More recently, cavity simultons have been demonstrated in synchronously-pumped degenerate optical parametric oscillators (OPOs) operating in the high-gain, low-finesse regime17. Such temporal cavity simultons are shown to have several favorable properties including broader bandwidths, which increase with increasing pump power, and higher efficiencies. When extended to the mid-infrared (mid-IR) regime18, where many important molecules have their strongest absorption features19, these properties make the simulton OPO a powerful frequency comb source for molecular sensing and spectroscopy.

In this work, we utilize the formation dynamics of quadratic cavity simultons for molecular sensing, in particular, the uniquely high sensitivity of simulton formation to the intracavity loss (Fig. 1a, b). In a proof-of-principle experiment sensing CO2 in a 1.2-m-long OPO operating in the simulton regime at around 4.18 μm18, we measure an equivalent path length enhancement of up to 6000 and additionally show a maximum sensitivity at concentrations of CO2 as high as atmospheric levels that is orders of magnitude larger than what can theoretically be achieved through linear methods using a source of equivalent power and bandwidth to the output of our broadband OPO. We additionally extend our experimental results to estimate a detector-limited normalized noise equivalent absorption (NEA) of 1.05 × 10−10 cm-1/\(\sqrt{{{{\rm{Hz}}}}}\) for realistic system parameters. Finally, we use numerical simulation to investigate the unique dynamics responsible for this sensing behavior and show the potential of the method to achieve high linearity across a dynamic range of 107.

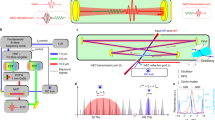
Fig. 1: Enhanced sensing using quadratic cavity simultons.
figure 1

a Schematic depiction of sensing in the simulton regime of a synchronously-pumped optical parametric oscillator at degeneracy. The bright soliton in the signal interacts with the sample every round trip, and the resulting competing nonlinear dynamics generate the measured signal response. b Specifically, stable simulton operation requires the simulton group advance, ΔT, to balance the round-trip group delay, ΔTRT, and the parametric gain to balance the sample loss, αsamp, and output coupling. c Schematic representation of linear absorption sensing governed by the Beer-Lambert Law for light interacting with a sample over a path length L. d Linear methods (light blue region) face limitations in the achievable sensitivity at high sample concentrations. In contrast, active cavity sensing with quadratic cavity (orange) can achieve high sensitivities at high sample concentrations. Trep, pump repetition period; Tcirc, pulse circulation time in the cavity; ΔT, simulton group advance; TRT, cold cavity round-trip time ΔTRT, round-trip group delay; χ(2), second-order susceptibility; ω, angular frequency; αsamp, sample absorption coefficient; OC, output coupling; Pin, input power; Pout, output power; L, path length; ℏ, reduced Planck’s constant.

Full size image

Sensing based on simulton formation dynamics enables a fundamentally different scaling behavior compared to typical linear absorption sensing following the Beer-Lambert Law20, as illustrated in Fig. 1c, d. In particular, although passive cavity enhancement21,22,23 can offer extremely high sensitivities at low analyte concentrations, the dynamic range is limited. For example, recent works24 have demonstrated normalized NEA values on the order of 10-13 cm-1/\(\sqrt{{{{\rm{Hz}}}}}\), while their dynamic range is constrained to about 4 orders of magnitude25 if not extended through a frequency26,27 or path-length multiplexed28 approach. By contrast, cavity soliton dynamics can achieve high sensitivity and significant signal enhancement even at large sample concentrations, thereby promising precision and extended dynamic range for mid-IR gas sensing while avoiding the typical requirements of high-finesse and high-power operation. Furthermore, in contrast to intracavity laser absorption sensing techniques29,30,31,32,33,34, cavity-simulton enhancement mitigates the limitations in sensitivity imposed by spontaneous emission and difficulty in measuring the low signal powers required for near-threshold operation29. Moreover, simultons can be achieved at arbitrary wavelengths, paving the way towards a universal molecular sensing scheme, especially in wavelength ranges where lasers are not readily available.

Results

Theory of cavity simulton formation

The simulton solution may be readily derived from the coupled wave equations describing a degenerate traveling-wave optical parametric amplifier for a pump at frequency 2ω and a signal at frequency ω, where only the nonlinear interaction and walk-off are considered (see Supplementary Note 7)15,16,17. The evolution of the bright-dark soliton pair in the signal and pump fields, Eω and E2ω, in the crystal is given by:

$${E}_{\omega }(z,t)=\frac{a}{\sqrt{2\tau }}{{{\rm{sech}}}} \left(\frac{t-T}{\tau }\right),$$
(1a)
$${E}_{2\omega }(z,t)=-{E}_{2\omega,0}\tanh \left(\frac{t-T}{\tau }\right).$$
(1b)

Here, Ej, jϵ{ω,2ω}, is the field amplitude of the jth wave, E2ω,0 is the pump amplitude, a is the simulton signal amplitude, T is the simulton centroid position, and τ is the simulton pulse width. We may use the nonlinear manifold projection method to find the evolution of T, τ, and a35. We assume an OPO with a nonlinear crystal of length l, a total cavity length of L, a round-trip group delay of ΔTRT, and a round-trip loss of coefficient of αω = αR + αsamp + αoth, where αR is the loss due to the output coupler reflectivity \(R={e}^{-{\alpha }_{R}L}\), αsamp is loss due to the sample, and αoth encapsulates all other round-trip losses. Then, the evolution of the system from the nth round trip to the n + 1th round trip is given by:

$$T(n+1)=\Delta T(n)+T(n)+\Delta {T}_{RT},$$
(2a)
$$\tau (n+1)={\tau }_{0},$$
(2b)
$$a(n+1)=\frac{a(n){e}^{\kappa {E}_{2\omega,0}l-{\alpha }_{\omega }\frac{L}{2}}}{\sqrt{1+\frac{a{(n)}^{2}}{{a}_{sim}^{2}}({e}^{2\kappa {E}_{2\omega,0}l}-1)}},$$
(2c)

where asim is the steady-state simulton amplitude, τ0 is the simulton pulse width, κ is the nonlinear coupling coefficient, and \(\Delta T(n)=-\frac{{\tau }_{0}}{2}\ln (1+\frac{a{(n)}^{2}}{{a}_{sim}^{2}}({e}^{2\kappa {E}_{2\omega,0}l}-1))\) is the simulton centroid shift due to nonlinear acceleration caused by pump depletion and subsequent back conversion.

From these equations, we see the requirements for stable cavity simulton formation, as depicted in Fig. 1b. Firstly, we see that achieving a non-zero steady-state amplitude requires that the gain balance the loss; here, this demands. Secondarily, the simulton centroid shift, ΔT, must balance the round-trip group delay due to the cavity length detuning, ΔTRT. This allows the simulton to re-synchronize with the pump, such that signal pulse circulation time Tcirc = TRT + ΔTRT + ΔT equals the pump repetition period, Trep. Further, we see the interdependence of these two conditions, as achieving a sufficient timing advance to compensate the round-trip delay requires a sufficient amount of gain and pump depletion, which results in the dynamics responsible for the simulton sensing mechanism.

Principle of simulton enhancement

The simulton-based sensing mechanism exploits the interplay between energy and timing in the simulton regime to attain high sensitivity to the sample of interest. The theoretical principle of threshold sensing as leveraged by the simulton sensing mechanism is depicted in Fig. 2a. For a given pump power, the addition of a small amount of loss due to the sample causes a threshold increase, resulting in a corresponding decrease in the output power, ΔP. The absolute change in power is proportional to the local slope efficiency at the sensing point, meaning a higher slope efficiency results in a higher sensitivity.

Fig. 2: Quadratic cavity simulton enhancement mechanism.
figure 2

a Theoretical behavior of near-threshold sensing, wherein the addition of sample causes an increase in threshold, resulting in a decrease in signal power at the sensing point. b The corresponding signal enhancement grows asymptotically as threshold is approached. c Experimentally measured input-output power relationships for the simulton (orange) and conventional (pink) regimes show the extremely high slope efficiency and high threshold of the simulton, suggesting its potential for near-threshold sensing with high SNR. Solid lines capture the trends through linear fits of the experimental data while the orange, dashed line shows the corresponding simulton simulation.

Full size image

In such a scenario, the corresponding equivalent path length enhancement is given by:

$$\frac{{L}_{eff}}{L}=\frac{-1}{L\Delta {\alpha }_{samp}}\ln \left(\frac{{P}_{signal}({\alpha }_{samp}+\Delta {\alpha }_{samp})}{{P}_{signal}({\alpha }_{samp})}\right)\approx \frac{\Delta {P}_{signal}}{L\Delta {\alpha }_{samp}{P}_{signal}},$$
(3)

where Leff is the effective path length, L is the cavity round-trip length and, equivalently, the sample interaction length, Psignal is the signal power, αsamp is the sample absorption coefficient, and Δαsamp represents a small change in the absorption due to the addition of sample. Simplified models using single-mode laser theory29 or OPO theory35,36 show the enhancement to asymptotically approach infinity as the number of times above threshold, N = Ppump/Pth, approaches unity, as shown schematically in Fig. 2b. Specifically, using degenerate OPO theory and assuming a round-trip loss in power for the signal of αω, we compute the equivalent path-length enhancement as:

$$\frac{\Delta {P}_{signal}}{L\Delta {\alpha }_{samp}{P}_{signal}}=\frac{1}{L{\alpha }_{\omega }}\frac{1}{\sqrt{N}-1}.$$
(4)

In typical intracavity laser systems, such threshold enhancement has been achieved through operation of the system close to the lasing threshold and subsequent addition of sample. In our degenerate OPO system, we show that such asymptotic enhancement may also be attained by pumping above the sample-free oscillation threshold, at a point Psense (Fig. 2a), and adding sufficient sample to raise the threshold to the level of the pump power. We benefit here from a feature of degenerate OPO systems that the addition of round-trip loss does not change the theoretical sensitivity, which contrasts single-mode laser theory (see Supplementary Notes 5–6). This enables tuning of the enhancement region through variation of the pump rate, thereby extending the dynamic range. In describing our results, therefore, we use N to describe specifically the number of times above the sample-free simulton threshold.

This large enhancement near threshold is theoretically followed by a decrease in the signal-to-noise ratio (SNR). However, the combination of the low spontaneous emission rate of the OPO37 as well as the large slope efficiency and high threshold in the simulton regime makes this SNR reduction extremely slow in comparison to other intracavity laser sensors. As an example, in our experiments (see Methods for details), the measured simulton threshold is approximately a factor of 2.5 larger than that of the conventional regime, and the slope efficiency is a factor of 3.5 larger, as illustrated in Fig. 2c. The net result is an ability to operate nearly 9 times closer to threshold in the simulton regime at the same output power for detector-limited measurements. This ability to achieve measurable signals very near to the simulton threshold can lead to an extremely large enhancement, making the simulton an ideal candidate for intracavity sensing.

From the fundamental perspective, such cavity-simulton-enhanced sensing cannot be achieved in a general multi-mode laser or conventional OPO as other modes which do not experience the absorption can compensate for the loss in the absorbing modes, leading to a limited change in the laser threshold or output power with the addition of the sample29. This is observed in the far above threshold conventional regime of our synchronously-pumped OPO but not for the simulton regime, as shown in Fig. 3a, b. Here, the experimental spectrum data in both the simulton (Fig. 3a) and conventional regimes (Fig. 3b) is given for three different intracavity CO2 concentrations. In the conventional regime, spectral modes which do not experience the absorption are observed to increase in power, largely compensating the loss due to the sample. In sharp contrast, the power in all the spectral modes of the simulton regime decreases nearly uniformly with the addition of even a narrow-band sample, mimicking that of a single-mode sensor for which threshold sensing is possible. In contrast to single-mode lasers, however, the simulton enhancement provides SNR advantages, can be achieved in wavelength ranges that are typically not easy to reach with lasers, particularly in the infrared, and provides broadband operation, which relaxes the requirement for fine tuning of the laser line to a single absorption line, though at the cost of selectivity without increasing system complexity.

Fig. 3: Simulton dynamics responsible for sensing.
figure 3

a Experimental power spectral densities demonstrate reduced power across the entire simulton spectrum with the addition of sample despite the relatively narrow CO2 absorption feature. b In the far above threshold conventional regime, like other general multi-mode lasers, power in non-absorbing modes increases with the addition of sample, largely compensating the loss in the absorbing modes. c Schematic depiction of the temporal dynamics of cavity simulton formation which enable the sensing enhancement mechanism. Additional loss in the round trip limits the ability of the simulton to deplete the pump and accelerate, leading to a reduced gain for all modes at steady-state. d Simulated steady-state pulse position as a function of gas concentration (left). Comparison with the theoretical gain window (right) shows the simulton moving further towards the gain window edge as the sample concentration is increased, in accordance with (c).

Full size image

This collective response of the spectral modes of the simulton to the addition of sample results from the interplay between the energy and timing requirements of simulton formation. This interplay is shown in Fig. 3c, where the formation of the simulton pulses over multiple round trips in the resonator is schematically depicted for two different values of the absorption. Due to the round-trip delay, ΔTRT, required for stable simulton formation, the newly formed pulse slowly falls out of the gain window, determined by the pump pulse and walk-off length, until it has grown enough to experience a sufficiently strong nonlinear acceleration to compensate the delay. The addition of a small amount of loss in the round trip to the signal will reduce the amount of acceleration and, correspondingly, the amount of gain experienced by all spectral modes of the simulton at steady-state as it interacts with the pump in the nonlinear crystal, leading to a spectrally uniform reduction of power despite the relatively narrow absorption spectrum, as shown in the measured spectrum of Fig. 3a.

This dynamical behavior is confirmed through our simulation. Figure 3d depicts the steady-state signal pulse position as a function of CO2 concentration (left) in comparison to the available gain (right) for three different number of times above threshold, N = 1.2 (green triangles), N = 1.35 (orange circles), and N = 1.5 (red squares). The gain here is calculated as the convolution between the pump pulse shape and the walk-off, with the center of the gain window positioned at 0 fs. The approximate gain window edge can be calculated by halving the sum of the pump pulse length and the walk-off length. Further details can be found in Supplementary Note 2. As sample is added to the cavity, the steady-state position of the signal pulse moves towards the gain window edge due to the reduced acceleration of the simulton until it no longer experiences sufficient gain to resonate. This sharp reduction in gain as sample is added to the cavity enables a high sensitivity for the simulton near threshold. Additional theoretical analysis and comparisons regarding the sensitivity, sensitivity enhancement, and SNR of single-mode intracavity lasers, single-mode degenerate OPOs, and simulton OPOs may be found in Supplementary Notes 5–7.

Sensing behavior

Figure 4a depicts the measured simulton output power as the CO2 concentration in the cavity is varied. Green triangles, orange circles, and red squares correspond to pumping at different number of times above threshold (here, N = 1.25, 1.64, and 1.84, respectively). Similar to the input-output power dependence shown previously, the output power dependence on CO2 changes most sharply close to threshold. Solid lines show linear fits of the near-threshold data. Their slope is used to find the sensitivity, with the highest fitted sensitivity calculated to be 4.1 mW/ppm. This unit of sensitivity is convenient as it both represents the slope of our calibration curve, defined at any concentration, and carries physical meaning as a detector-independent metric for characterizing the strength of the system response to the addition of sample. Additionally, it allows for easy analytical comparison with linear absorption spectroscopy through the Beer-Lambert Law. Finally, we observe that by tuning the pump power, one can change the region of high sensitivity, thereby extending the dynamic range of the system.

Fig. 4: Sensing behaviors of quadratic cavity solitons.
figure 4

a Measured output power as a function of CO2 concentration for different number of times above threshold, N. A high sensitivity of 4.1 mW/ppm is measured near threshold, emphasized using the solid trend lines. b Simulations of the simulton response to the addition of CO2 at various number of times above threshold exhibit good qualitative agreement with the experimental data. c Equivalent path-length enhancement calculated for neighboring points in the experiment, showing a measured enhancement as large as 6000. Solid lines show the expected asymptotic enhancement corresponding to the linear fits in (b), with dashed lines extending these fits to enable extrapolation of detector-limited enhancements for detection bandwidths of 1 MHz (x’s) and 1 Hz (stars). d Simulated change in output power as a function of CO2 concentration with a linear fit (dashed line) showing good linearity over a dynamic range of 107. e Measured sensitivity as a function of CO2 concentration in direct comparison with linear sensing (light blue), demonstrating orders of magnitude sensitivity improvement over linear methods at high sample concentrations.

Full size image

These observations are consistent with our simulated sensing results, shown in Fig. 4b. Here, we again see the large sensitivity near threshold and tuning of the sensitive region through variation in the number of times above threshold. The calculated sensitivity is also shown to be consistent across the different pump conditions. Our simulated sensitivity is slightly lower than what is observed experimentally, which we attribute primarily to imperfections in our modeling of the gas response.

We also find the equivalent path length enhancement for the experimental data, as shown in Fig. 4c. To do so, we define Δαeff as the effective absorption coefficient experienced by a pump of the same bandwidth as the simulton which has experienced 1.2 m of CO2 absorption at the reference concentration. Using this, we calculate \(\frac{-1}{L\Delta {\alpha }_{eff}}\ln (\frac{{P}_{signal}({\alpha }_{eff}+\Delta {\alpha }_{eff})}{{P}_{signal}({\alpha }_{eff})})\) for neighboring points in our experimental measurement. Further details on this calculation may be found in Supplementary Note 3. The largest enhancement of 6000 is observed near threshold for the case where N = 1.84, though similar enhancements are observed near threshold for the other cases. Solid lines show the enhancement corresponding to the linear fits from Fig. 4a in accordance with theory. The close fits near threshold illustrate the nearly asymptotic trend for the enhancement, with deviations at lower sample concentrations coming from the observed saturation of the simulton response far above threshold.

To additionally demonstrate the potential of this asymptotic enhancement, we extend the theoretical fits (dashed lines) and plot the detector-limited enhancement for two different measurement bandwidths, 1 MHz (x’s) and 1 Hz (stars). We select these bandwidth values as the current measurement is performed at a 1 MHz bandwidth, while 1 Hz is the standard for normalized comparison with other reported results. The detector-limited value is found by dividing our noise-equivalent power (NEP), given by the 1σ variance of our detector noise, by our measured sensitivity (see Supplementary Note 3 for more information). For output powers of 74 μW and 74 nW, the calculated NEPs at a 1 MHz and 1 Hz bandwidth, respectively, we see enhancements on the order of 100s of thousands and 10s of millions.

In addition to the estimated enhancement, we compute the detector-limited normalized NEA, which we find to be 1.05 × 10−10 cm-1/\(\sqrt{{{{\rm{Hz}}}}}\), corresponding to a concentration of 18 ppt. Taken in tandem with our experimentally measured concentrations of up to nearly 400 ppm, this is suggestive of a dynamic range on the order of 107 for the method, which can be further extended through use of a higher-power pump laser. To further validate this estimated dynamic range, we use our simulation to characterize the linearity of the sensor response across many orders of magnitude of CO2 concentrations. The results are plotted in Fig. 4d, where the y-axis, ΔP, indicates the difference between the output power at a given concentration and the power at 0 ppm. A dashed line indicates a linear fit of the data, with solid lines showing the detector limits for measurement bandwidths of 1 Hz and 1 MHz. Here, we again see that sample concentrations can be measured down to the level of 10s of ppt, and good linearity is observed over nearly 7 orders of magnitude of dynamic range. While such detector-limited measurements would require careful stabilization of the measurement system and finer control over the measured gas concentration than was achieved in the present experiment, which is currently limited by the precision of our reference sensor (see Supplementary Note 1), these theoretical values show high potential for the simulton sensing mechanism.

Finally, we can make direct comparisons with the sensitivity achievable using linear methods for varying concentrations. Figure 4e shows the sensitivity in mW/ppm, calculated for neighboring points in our experimental measurement. Note that through variation of the number of times above threshold, a sensitivity near the measured value of 4.1 mW/ppm may be achieved across all concentrations.

By comparison, we have plotted the theoretically achievable sensitivities using linear methods (light blue region). Here, we model a linear cavity pumped by a pulsed source with the same bandwidth as our measured simulton and an average power of 500 mW, equivalent to the sample-free output power of the simulton OPO for the highest pump power. We have additionally assumed a path-length-multiplexed approach in which the path length enhancement is varied to achieve the maximum sensitivity at each point, up to a length corresponding to an enhancement of 106 and corresponding finesse of over 1.5 million for a cavity length of 1.2 m, equivalent to the length of our OPO, compared to our cavity finesse of 2. We believe this to be a large enough enhancement limit for linear methods to represent practically achievable values of the finesse. Further discussion and additional points of comparison, including with single-mode systems, may be found in Supplementary Note 3. Though high sensitivities can be maintained at low concentrations for this path-length-multiplexed approach, an inverse scaling is observed in accordance with theory, emphasizing the limitations of linear techniques for achieving high sensitivities at high sample concentrations. In contrast, the nearly constant and orders of magnitude higher sensitivity demonstrated by the simulton sensing mechanism at high sample concentrations illustrates the potential for this method to achieve precision at large concentrations, which can benefit many applications while avoiding the typical requirements of high-finesse cavities.

Discussion

It is worth noting that other methods exist which address some of the aformentioned limitations of linear absorption sensing, including dispersion sensing as well as photoacoustic and photothermal sensing. Dispersion spectroscopy techniques achieve high linearity and consequently large dynamic range through direct measurement of the refractive index rather than the absorption of the sample of interest38. A recent demonstration of cavity-mode dispersion spectroscopy39, which marries the benefits of dispersion spectroscopy with cavity-enhanced techniques, has achieved a dynamic range of 2 × 105 and a NEA of 5 × 10−11 cm-1. Photothermal and photoacoustic methods work by measuring the heat-induced refractive index change and pressure change due to the absorption of light by the sample, respectively. A recent demonstration of mode-phase-difference photothermal spectroscopy40 has shown a dynamic range of 2 × 107 and a NEA of 1.6 × 10−11 cm-1. Meanwhile, measurements using intracavity quartz-enhanced photoacoustic spectroscopy41 have exhibited a dynamic range of  >105 and a normalized NEA of 1.5 × 10−8 cm-1/\(\sqrt{{{{\rm{Hz}}}}}\). As these results show, these methods demonstrate effective ways of overcoming limitations of absorption-based sensing but at the cost of introducing additional system complexity and potential susceptibility to environmental noise.

The sensing performance of the simulton could be further improved in several ways. Here, we have only explored the first simulton due to limitations in our pump power, but OPOs will often exhibit multiple simulton peaks as the cavity length is further increased. These further-detuned simultons can exhibit even higher slope efficiencies, leading to potentially larger sensitivities and sensitivity enhancements17. Additionally, simultons benefit from operation in the high-gain, low-finesse regime. Recent advances in thin-film lithium niobate nanophotonics, where gains as large as 100 dB/cm have been demonstrated42,43, could push OPOs even further into this regime, adding to a growing push for the creation of high-sensitivity, highly scalable molecular sensors44,45,46. Low-finesse operation also makes simulton-based sensing compatible with waveguide structures such as slot47 and suspended rib waveguides48 aimed at improving evanescent wave interaction with the molecular sample of interest but generally at the cost of additional propagation loss. Finally, other nonlinear behaviors in OPOs such as spectral phase transitions offer additional means to achieve high sensitivity for intracavity sensing in OPOs49. Exploration of different operation regimes of OPOs for molecular sensing will be the subject of future work.

There are a few additional considerations for use of the simulton enhancement mechanism for practical sensing applications. The first is with regards to selectivity, as previously noted. Since the simulton response is broadband, the ability to distinguish between molecules using the simulton response alone can be limited, so care must be taken in the system design to ensure that only the molecule of interest is captured in the simulton bandwidth. With that said, one may also perform a spectrally-resolved measurement of the output signal to gain information about the molecules present. Additionally, since other regimes of OPO operation contain different frequency content, exploration of other OPO regimes could enable multi-species sensing using only a detector for signal read-out (see Supplementary Note 4)50. Secondly, to achieve the theoretically suggested detector-limited performance, one must ensure that other noise contributions are minimized; in particular, the relative intensity noise (RIN) is of concern. Here, we consider the signal RIN as being dominated by the RIN of the pump, coupled into the signal through the slope efficiency. To remain detector-noise limited, we require that the signal RIN in a 1 Hz bandwidth is less than the NEP of 74 nW. Considering our measured slope efficiency of 128% and 665-mW threshold, this would necessitate a pump RIN of less than −70.5 dBc/Hz. Such a value is practically achievable in many mode-locked fiber laser systems51, among other pulsed sources.

In summary, we have proposed and demonstrated a mid-IR molecular sensing mechanism which benefits from the formation dynamics of quadratic cavity simultons in OPOs to achieve strong performance. Our proof-of-principle experimental demonstration measuring CO2 in an OPO at 4.18 μm and complementary simulations show an equivalent path length enhancement of 6000 and orders of magnitudes sensitivity enhancement at large gas concentrations when compared to linear cavity-enhanced methods. This distinct scaling behavior of the simulton suggests the potential for achieving high sensitivity, large dynamic range, and good precision using this method, in accordance with our theoretical estimates of the detector-limited performance in the current experimental configuration, and illustrates how nonlinear dynamics in low-finesse resonators may be exploited for enhanced sensing.

Methods

Experimental procedure

Experiments are conducted in a degenerate, synchronously pumped, free-space OPO in a bow-tie formation18. The pump is the output of a periodically poled lithium niobate-based OPO which provides a pulse train at 2.09 μm with a 155 nm bandwidth, a 250 MHz repetition rate, and up to 1.4 W of average power. Pulses are coupled in through a dielectric-coated mirror with high transmission for the pump and high reflection for the signal. The input coupler is placed on a stage with a piezoelectric actuator for tuning of the cavity length. Nonlinearity is provided by a 0.5 mm, anti-reflection coated, plane-parallel, orientation-patterned gallium phosphide crystal with a poling period of 92.7 μm for type-0 phase-matching between the pump at 2.09 μm and signal at 4.18 μm at room temperature. Two concave gold mirrors with radius of curvature of 24 mm on either side of the crystal provide focusing and collimation. The output coupler is a dielectric-coated mirror which allows 25% output coupling for the signal. The output is passed through a long-pass filter and sent to a MCT detector for monitoring. Spectrum measurements are performed using a commercial Fourier-transform infrared spectrometer.

The OPO and all measurement equipment are placed inside a nitrogen purging box. To perform the sensing measurement, the atmospheric gases present in the cavity are flushed through addition of N2 to the setup, with the dominant system response being attributable to atmospheric CO2 (see Supplementary Note 4). This CO2 concentration is referenced to a commercially available CO2 sensor for calibrating the measurements. At each concentration, five data points are taken and averaged to produce the final result. Further details on the experimental setup and procedure can be found in Supplementary Note 1.

Numerical simulation

Numerical simulations are performed following the methods described in ref. 17. The nonlinear propagation through the crystal is computed using the Fourier split-step method to solve the coupled wave equations describing the pump and signal evolution, which may be written as:

$${\partial }_{z}{E}_{\omega }(z,t)=\kappa {E}_{2\omega }{E}_{\omega }^{*}-\frac{{\alpha }_{\omega }}{2}+{\hat{D}}_{\omega }{E}_{\omega },$$
(5a)
$${\partial }_{z}{E}_{2\omega }(z,t)=-\kappa {E}_{\omega }^{2}-\frac{{\alpha }_{2\omega }}{2}-\Delta {\beta }^{{\prime} }{\partial }_{t}{E}_{2\omega }+{\hat{D}}_{2\omega }{E}_{2\omega },$$
(5b)

where Eω and E2ω represent the field envelopes, normalized such that \({| {E}_{j}| }^{2}\), jϵ{ω,2ω}, is the instantaneous power in the jth wave, \(\Delta {\beta }^{{\prime} }={v}_{g,2\omega }^{-1}-{v}_{g,\omega }^{-1}\) is the group velocity mismatch, where vg,j is the group velocity of the jth wave, αj is the loss in power of the jth wave, \({\hat{D}}_{j}=\mathop{\sum }_{m=2}^{\infty }\left[\frac{{(i)}^{m+1}{\beta }_{j}^{(m)}}{m!}\right]{\partial }_{t}^{m}\) is the dispersion operator describing the material dispersion experienced by the pump and signal in the crystal, where \({\beta }_{j}^{(m)}\) describes the mth-order dispersion of the jth wave, and \(\kappa=\frac{\sqrt{2{\eta }_{0}}\omega {d}_{eff}}{{n}_{\omega }{w}_{0}\sqrt{\pi {n}_{2\omega }c}}\) is the nonlinear coupling coefficient, where deff is the effective nonlinearity, nj is the refractive index of the jth wave, c is the speed of light, η0 is the impedance of free space, and w0 is the beam waist of the signal, assuming the pump and signal to be confocal Gaussian beams. Here, the reference frame for the time coordinate is taken to be co-moving with the signal, and a π/2 phase shift has been applied the pump field, E2ω, to permit real solutions.

The round-trip propagation is given by a linear filter which includes both the dispersion and frequency-dependent loss. Important to simulating the sensing behavior is an appropriate model for the gas absorption and dispersion in the round trip. For this, we use a Lorentz oscillator model, with parameters taken from HITRAN52. Further information on our numerical simulations can be found in Supplementary Note 2.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.