Introduction

Density fronts are ubiquitous features in the global ocean, and act as a key mediator for the exchange of climatically-important properties, such as heat and carbon dioxide, between the upper ocean and the atmosphere1,2,3. Yet, despite the fronts’ significant climatic role, the current generation of climate-scale ocean models cannot adequately represent the lifecycle of fronts, due to the models’ overly coarse resolution and the underdeveloped state of parameterizations of frontal processes.

The mechanism leading to frontal formation is known as frontogenesis, and it can occur in the ocean across a breadth of scales extending from tens of kilometers to a few hundreds of meters4. At mesoscales (horizontal scales of 20–300 km, periods of weeks-months), the classical deformation frontogenesis model of Hoskins and Bretherton (1972)5 is thought to apply, and describes a scenario in which a confluent strain field near the ocean surface leads to the sharpening of pre-existing density contrasts. Despite this two-dimensional deformation framework’s many successes at rationalizing frontal dynamics in the atmosphere and ocean6,7,8, more recent theoretical and modeling studies have provided insights into the extension of frontogenesis down to the oceanic submesoscale range (horizontal scales of 0.2–20 km, periods of hours-days). These studies postulate a significant role for the ageostrophic circulations in the upper ocean that result from mixed-layer instabilities9 and boundary layer turbulence10.

The convergence of the horizontal velocity field, referred to as horizontal convergence (i.e. negative horizontal divergence), can drive frontogenesis, as initially demonstrated in earlier theories of dynamic meteorology5,11,12. For oceanic fronts, Barkan et al. (2019)13 derived an asymptotic model to illustrate that near-surface convergent flows can determine gradient sharpening rates in the submesoscale range. They demonstrated that, for anisotropic fronts and filaments that are typically characterized by O(1) Rossby numbers14, a straightforward relationship emerges: the rate of frontal sharpening is equal to the magnitude of horizontal convergence. This correspondence offers predictive capabilities for the growth of vorticity, divergence, and buoyancy gradients. The theory posits that the presence of horizontal convergence at the frontal zone invariably leads to super-exponential growth, a principle that extends beyond two-dimensional models to encompass three-dimensional complexities. Our observational findings in this study are consistent with this theoretical framework, and thus suggest a central role of horizontal convergence in determining the frontogenetic processes in the submesoscale range (i.e. submesoscale frontogenesis).

Submesoscale fronts, which form through submesoscale frontogenesis, are particularly effective at inducing intense vertical velocities in the upper ocean, with submesoscale vertical velocities of O(100 m day−1) typically being an order of magnitude larger than mesoscale vertical velocities of O(10 m day−1)15,16. Convergent vertical motions at submesoscale fronts can effectively concentrate surface materials, and subsequently inject them into the ocean interior17,18,19. Another important aspect of the submesoscale frontogenetic process is its driving of intense ageostrophic secondary circulations that lead to a front-focused forward kinetic energy cascade. While some forward energy transfer can occur locally under mesoscale strain-induced frontogenesis, only in the submesoscale frontogenesis scenario it becomes significant and occurs at a rate that is proportional to the frontal convergence20. Given the ubiquity of fronts, submesoscale frontogenesis may thus represent an important sink within the ocean’s energy balance21. This is in contrast to the direct action of mixed-layer and mixed-transitional layer instabilities, which are often shown by submesoscale-permitting simulations to generate near-balanced submesoscale eddies conducive to an inverse energy cascade22,23,24,25,26. Submesoscale frontogenetic processes and fronts are found to be excessively dampened in these submesoscale-permitting simulations27. At any rate, the observational evidence for this emerging view of convergent flow-driven submesoscale frontogenesis is rare28, so that a systematic test with process-targeted measurements is needed.

Here, we aim to provide such test by investigating the mechanism of submesoscale frontogenesis, its associated cross-scale energy cascade, and its dynamical context, in a typical mid-latitude ocean region. With this goal in mind, we analyse a unique suite of in situ observations acquired by a nested mooring array over a full annual cycle (see “OSMOSIS data and processing” in Methods and Supplementary Fig. 1). Our results are in good agreement with the recent theoretical characterizations of submesoscale frontogenesis described above, in that they reveal that: (i) frontogenesis is enhanced in the submesoscale range; (ii) it is underpinned by convergent upper-ocean flows; and (iii) it is associated with a rapid forward kinetic energy cascade toward dissipative scales.

An observed submesoscale frontogenesis event

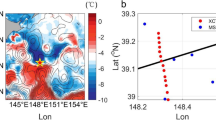
The occurrence of submesoscale frontogenesis and its associated downscale kinetic energy transfer in our study area is initially illustrated by focusing on a specific wintertime event (Fig. 1). Images of altimetric sea surface height anomaly and high-resolution sea surface temperature show that the mooring array was positioned on the cold (cyclonic) side of a front on 7 February 2013 (Fig. 1a, b). The sea surface temperature changed by > 1 °C over a few kilometers at the edge of the front.

Fig. 1: Wintertime submesoscale frontogenesis event.
figure 1

a Snapshot of sea surface height anomaly in the Ocean Surface Mixing, Ocean Submesoscale Interaction Study (OSMOSIS) observational region on 7 February 2013, with surface geostrophic current velocity shown as black vectors. Sea surface height anomaly and surface geostrophic velocity data are obtained from the delayed-time gridded 0.25° × 0.25° Archiving, Validation and Interpretation of Satellite Oceanographic Data (AVISO) product. b Visible and Infrared Imaging Radiometer Suite (VIIRS) sea surface temperature image on 7 February 2013 at 14:07 UTC, with the OSMOSIS moorings indicated as white dots and a 2 km distance scale shown in white for reference. Data missing due to cloud cover are shaded in gray. The location of the VIIRS image is marked with a pink box in (a). Time series of (c) potential density ρ, (d) kinetic energy (KE), (e) normalized horizontal convergence  − δ/f, (f) normalized frontogenetic rate Tb/f, (g) vertical velocity w, and (h) energy transfer rate \({\Pi }_{\omega }^{2d}\) estimated at the central mooring from 7–9 February, 2013. The black lines indicate the glider-derived mixed layer depth, and the vertical dashed lines denote 14:07 UTC on 7 February 2013 in (c–h).

Full size image

During this time, the mooring array measured the upper ocean to be weakly stratified, with the mixed layer deepening rapidly from 200 m down to > 300 m and then shoaling to about 150 m within 1 day (Fig. 1c). The measured kinetic energy was greatly elevated and surface-intensified during the mixed layer deepening (Fig. 1d), corresponding to a maximum horizontal velocity of about 0.38 m s−1. The enhanced kinetic energy in the mixed layer was concurrent with predominantly positive frontogenetic rate (Tb  >  0) and horizontal convergence (−δ >  0), reaching respective maximum values of 0.59f and 0.76f, where f is the Coriolis parameter (Fig. 1e, f).

Persistent upper-ocean horizontal convergence implies downwelling in underlying layers. Vertical velocity was directly estimated using the non-diffusive density equation29, and intense downwelling of order— 100 m day−1 was indeed seen below the mixed-layer base during this frontogenetic event (Fig. 1g). Lastly, the rate of cross-scale kinetic energy transfer was quantified by applying the coarse-graining approach to the mooring data27,30,31,32. An enhanced forward energy cascade, at a rate of about 10−7 m2 s−3, was found, which is an order of magnitude larger than the winter-mean energy transfer rate (Fig. 1h; also see Supplementary Fig. 2). This event is analogous to that reported by D’Asaro et al. (2018)28, in which rapid horizontal convergence of a large number of surface drifters was observed on the dense side of a front in the northern Gulf of Mexico, accompanied by strong sinking of water at the front.

Features of submesoscale turbulence over an annual cycle

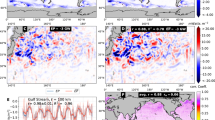
The success of the mooring array in quantifying the frontogenetic event described above motivates us to explore the mechanism and effects of submesoscale frontogenesis over the entire year of observations. To begin with, we examine the degree to which subinertial flows depart from geostrophic balance, which is a measure of the importance of ageostrophic motions. A 24 h low-pass filter is applied to mooring velocity and density measurements to remove variability in the internal wave band (see “OSMOSIS data and processing” in Methods). Departure from geostrophy can be assessed by comparing the vertical shear of horizontal velocity at the central mooring to the horizontal gradient of buoyancy across horizontal scales from 18 km – 2 km (Fig. 2a–c).

Fig. 2: Year-long time series of vertical shear and horizontal buoyancy gradient.
figure 2

a–c Finite-difference configurations used to compute horizontal gradients of velocity and buoyancy at, respectively, horizontal scales of 18 km, 9 km and 2 km from the mooring array observations. d Depth-resolved time series of vertical shear, \({U}_{z}=\sqrt{{(\frac{\partial u}{\partial z})}^{2}+{(\frac{\partial v}{\partial z})}^{2}}\), estimated at the central mooring. The black line indicates the glider-derived mixed layer depth. e Time series of depth-averaged horizontal buoyancy gradient, ∣∇hb∣, estimated at horizontal scales of 18 km, 9 km and 2 km from the mooring array observations. Gray blocks in (d-e) indicate time periods of winter frontal events, defined by the region hosting \(-{\bar{\delta }}^{2d} > \) 0.3.

Full size image

The vertical shear Uz is found to be highly variable and frequently deep-reaching down to 500 m throughout the year, attaining magnitudes of order 10−3 s−1 within and below the mixed layer (Fig. 2d). The horizontal buoyancy gradient ∣∇hb∣ generally follows the vertical shear closely over the annual cycle, but exhibits a dependence on horizontal scale (Fig. 2e). Notably, the horizontal buoyancy gradient magnitude at 2 km is considerably larger than those at 9 km and 18 km, with respective winter root-mean-square (RMS) values of 5.5 × 10−8, 3.5 × 10−8 and 2.6 × 10−8 s−2. This indicates the increased sharpening of fronts in the submesoscale range. At the 2-km scale, the daily-averaged magnitude of the horizontal buoyancy gradient term ∣∇hb∣/f is systematically larger than that of the vertical shear term Uz in the thermal wind balance equation (Supplementary Fig. 3). This denotes that the observed upper-ocean subinertial motions at that scale contain a substantial ageostrophic component (i.e. ageostrophic flows not associated with internal waves). The concurrent occurrence of sharper horizontal buoyancy gradients and stronger ageostrophic motions at the 2 km scale points to a common underpinning by submesoscale frontogenesis.

A window into the dynamics of submesoscale frontogenesis is provided by comparing the normalized frontogenetic rate Tb/f, horizontal convergence  − δ/f and relative vorticity ζ/f across the 18 km, 9 km and 2 km horizontal scales sampled by the mooring array (see “Kinematic properties” in Methods). All variables consistently display pronounced seasonality and scale dependence, with larger amplitudes in winter and at smaller scales (Fig. 3a–c). The quantities diagnosed at 2 km scales are more surface-intensified, with RMS values of Tb/f and  − δ/f peaking at 0.3, and those of ζ/f approaching 0.5 near the surface. The comparable magnitudes of  − δ/f and ζ/f at 2 km scales indicate that horizontally convergent flows play an increasingly important dynamical role at smaller scales, consistent with a progressive breakdown in geostrophic balance. In contrast, the RMS values of all variables at 9 km and 18 km have magnitudes of order 0.1, approximately a factor of 4 smaller than those at 2 km.

Fig. 3: Statistics as a function of horizontal scale and season.
figure 3

Depth-resolved (a–c) root-mean-square (RMS) and (d–f) skewness of the normalized frontogenetic rate Tb/f, horizontal convergence  − δ/f, and relative vorticity ζ/f, estimated at horizontal scales of 18 km, 9 km and 2 km during winter (solid) and summer (dashed).

Full size image

A positive skewness in frontogenetic rate, horizontal convergence, and relative vorticity at 2 km scales is observed only in winter (Fig. 3d–f). Such skewness values are consistent with previous modeling and observational studies of submesoscale turbulence33,34,35,36,37. Frontogenetic rate and horizontal convergence are positively skewed above 200 m, while the skewness of vorticity extends down to below 450 m, with skewness decreasing gradually from 1.5 at 50 m t < 0.5 below 200 m. These asymmetric distributions indicate that active submesoscale turbulence is at play in the wintertime upper ocean, with more extensive occurrence of frontogenetic processes, horizontal convergence, and cyclonic vorticity there. The positive skewness in upper-ocean layers illustrates our study area’s generic propensity to host submesoscale frontogenesis. By contrast, no skewness features are seen at larger scales or in summer. Overall, these diagnostics indicate that nonlinear ageostrophic dynamics are increasingly important for frontogenetic processes, down to the sampled scales of O(1 km).

Submesoscale frontogenesis induces a forward energy cascade

To substantiate our demonstration of the central involvement of convergent flows in submesoscale frontogenesis, we construct scatterplots of daily-averaged horizontal convergence  − δ/f versus frontogenetic rate Tb/f at horizontal scales of 18 km, 9 km and 2 km (Fig. 4). At 2 km scales,  − δ/f and Tb/f are strongly correlated, with a correlation coefficient R2 of ~0.78 (p  < 0.01), and closely follow a one-to-one relationship as predicted by the theory of Barkan et al. (2019)13. However, this correlation between  − δ/f and Tb/f is also scale-dependent. As the resolved horizontal scales decrease, the correlation coefficient R2 between  − δ/f and Tb/f reduces to ~0.3 (p  < 0.01) at 9 km scales and 0.11 (p > 0.05) at 18 km scales. In contrast to horizontal convergence, neither relative vorticity ζ/f nor strain rate α/f are significantly correlated with Tb/f at any scale, with correlation coefficients R2 almost always < 0.2 and p-values exceeding 0.05 across all resolved scales (Supplementary Fig. 4). This further suggests that the strong convergent flows—and not strain—are most likely the main factor in governing submesoscale frontogenesis.

Fig. 4: Relationship between the rate of frontal sharpening and horizontal convergence across horizontal scales.
figure 4

Scatter plots of the daily-averaged normalized frontogenetic rate Tb/f and the normalized horizontal convergence  − δ/f in winter, estimated at horizontal scales of (a) 18 km, (b) 9 km and (c) 2 km for all observed depths. The correlation coefficient R2 and p-value are indicated, and illustrate the agreement with the submesoscale frontogenesis theory of Barkan et al. (2019)13 at finer horizontal scales.

Full size image

We further explore the effects of submesoscale frontogenesis on the cross-scale kinetic energy transfer, by applying the filter-based coarse-graining framework to compute energy fluxes across temporal scales (see “Kinetic energy transfer” in Methods). The rates of energy transfer for a filter scale of 2 days (\({\Pi }_{\omega }^{2d}\), representing the horizontal kinetic energy transfer from flows with temporal scales > 2 days to those with shorter periods) during frontal and non-frontal periods in winter are compared in Fig. 5a. Here, oceanic fronts are defined as the ninetieth percentile of the horizontal convergence (\(-{\bar{\delta }}^{2d} > \) 0.3, where \({\bar{\delta }}^{2d}\) is the divergence smoothed over the same 2-day scale for consistency; frontal periods are shown in Fig. 2d). Similar results are found when considering a lateral buoyancy gradient threshold for defining fronts, and when using a longer or shorter period for computing cross-scale kinetic energy transfer rate (Supplementary Figs. 5–6). The 2 day period corresponds to a horizontal scale of ~ 8 km, where this scale was determined via a frequency-resolved structure function analysis38. This horizontal scale is in line with the transition scale of 6–10 km for a change to increasingly nonlinear ageostrophic dynamics in the California Current System, identified using a cross-spectral phase approach39.

Fig. 5: Forward energy cascade associated with submesoscale frontogenesis.
figure 5

Depth profiles of (a) \({\Pi }_{\omega }^{2d}\), the coarse-grained horizontal kinetic energy flux from time scales > 2 days to shorter periods, (b) \(-{\bar{\delta }}^{2d}/f\), the normalized horizontal convergence smoothed at a 2 day scale, (c) \(K{E}^{{\prime} 2d}\), the kinetic energy of time scales < 2 days, and (e) w2d, the root-mean-square of vertical velocity smoothed at a 2 day scale, demonstrate the enhanced forward cascade and vertical motion at frontal regions, where the horizontal convergence is stronger. d Profiles of \({\Pi }_{\omega }^{2d}\) versus \(-{\bar{\delta }}^{2d}K{E}^{{\prime} 2d}\) (the quantities of (b) and (c)) at frontal regions demonstrate the agreement with the theoretical predictions of Srinivasan et al. (2023)20. Shaded areas in (a–e) denote the 95% confidence level. Here fronts are defined by the region hosting \(-{\bar{\delta }}^{2d} > \) 0.3.

Full size image

Both front-averaged and winter-averaged energy transfers are positive in the upper ocean, that is, directed from temporal scales > 2 days toward shorter scales (i.e. a forward transfer). The front-averaged forward transfer is two times larger than the winter-averaged flux, indicating that the energy flux across the 2 day scale is concentrated at fronts. The horizontal convergence (\(-{\bar{\delta }}^{2d}\)) and the kinetic energy at scales < 2 days (\(K{E}^{{\prime} 2d}\)) are also enhanced at fronts relative to the winter averages (Fig. 5b, c). We also find a near-linear scaling between \({\Pi }_{\omega }^{2d}\) and \(-{\bar{\delta }}^{2d}K{E}^{{\prime} 2d}\) (Fig. 5d), consistent with the numerical investigation of Srinivasan et al. (2023)20. Further, the diagnosed vertical velocity at fronts, with RMS value exceeding 70 m day−1, is substantially larger than the RMS value of vertical velocity during the entire winter (Fig. 5e and see “Vertical velocity” in Methods). In conclusion, all of the key predictions of the emergent view of submesoscale frontogenesis as a horizontal convergence-linked mechanism stand to our observational test.

Discussion

Our observations reveal that upper-ocean convergent flows are responsible for the rapid development of submesoscale frontogenesis down to O(1 km) scales, and that they are associated with a forward cascade of kinetic energy. This finding differs crucially from the quasi-geostrophic or surface quasi-geostrophic view of frontogenesis12,40, in which the sharpening of buoyancy gradients can occur passively in the absence of horizontal convergence, and where an inverse kinetic energy flux is always found41,42. Further, the idealized semi-geostrophic model of Hoskins and Bretherton (1972)5 does not predict horizontal convergence to be the dominant frontogenesis agent, nor do the surface semi-geostrophic simulations43,44 predict the skewness levels in vorticity and horizontal convergence concurrent to a forward energy cascade reported here.

It is difficult to determine from our observations whether horizontal convergence-driven submesoscale frontogenesis arises naturally at a later stage of mesoscale strain-induced frontogenesis, or if submesoscale mixed-layer eddies and boundary-layer turbulence are the dominant frontogenetic agents. The submesoscale frontogenetic rate, horizontal convergence, and relative vorticity that we observe are all surface-intensified, but also deep-reaching during winter, suggesting that mixed transitional layer instability may also be at play26,36. These mechanisms likely coexist, and collectively contribute to the generation of ageostrophic secondary circulations that initiate horizontally convergent flows and submesoscale frontogenesis. Additionally, super-inertial submesoscale motions, which are thought to exhibit strong ageostrophic characteristics45, may further promote submesoscale frontogenesis and the associated forward energy flux, but these effects are not examined in this study. Previous OSMOSIS works have highlighted the role of mesoscale frontogenesis in the filamentation of submesoscale fronts, pre-conditioning the occurrence of various kinds of forced submesoscale instabilities and resulting in upper-ocean restratification and downscale energy transfer from mesoscale to submesoscale flows27,46,47. While the observed downscale energy transfer does not seem to significantly alter the turbulent kinetic energy budget at a fixed depth of around 50 m compared to the influence of surface winds and waves48, its relative importance becomes much more pronounced during transient frontal events when considering the mixed layer’s integrated energy budget49. Our study provides observational evidence that frontogenesis at the submesoscale is strongly associated with the horizontal convergence induced by ageostrophic secondary circulations, and that it can effect a forward energy cascade.

In any event, the comparable magnitudes of horizontal convergence and relative vorticity found here agree with drifter observations in the Gulf of Mexico28, and indicate that submesoscale frontal dynamics are inconsistent with the classical regime of Hoskins and Bretherton (1972)5—in which relative vorticity always exceeds horizontal convergence by an order of magnitude. Numerical investigations with sufficiently high resolution (~500 m) serve to illustrate this generic behavior of submesoscale frontogenesis22,35,50,51. Such studies reveal a characteristic pattern during winter: robust cyclonic vorticity consistently prevails along frontal interfaces, and is closely associated with horizontal convergence levels that approximate the vorticity magnitudes. Interestingly, the submesoscale frontogenesis theory of Barkan et al. (2019)13 predicts the dominance of convergent flows to occur only for RMS ζ/f values of O(1). However, our observations show that this dynamical regime prevails even for modest values of RMS ζ/f< 0.5, suggesting that the theory may hold beyond its regime of formal validity.

An important implication of the present work is that, if submesoscale frontogenesis is horizontal convergence-determined, the ocean will be dynamically enabled to generate sharp fronts more rapidly and, concurrently, to produce larger upper-ocean vertical velocities. Despite occurring on small spatial scales, the growth in horizontal convergence and submesoscale frontogenesis rate commonly extend beyond the mixed-layer base. This finding suggests that the upper ocean is substantially more effective at mediating vertical exchanges between the atmosphere and interior than portrayed by either the Hoskins and Bretherton paradigm or non-submesoscale-resolving models. Our highlighted mechanism is not yet represented by standard submesoscale parameterizations, however52,53. The rapid vertical exchange caused by submesoscale frontogenesis can help explain the asymmetry in upper-ocean ventilation found between cyclones and anticyclones54. Horizontally, the convergent upper-ocean flows accumulate buoyant materials such as microplastics and phytoplankton, with implications for ecosystems, fisheries and biogeochemistry55,56.

Present submesoscale parameterizations primarily focus on the generation mechanisms of mixed-layer eddies and their associated restratification effects, while also accounting for vertical mixing in the surface boundary layer52,57,58. Recently, Zhang et al. (2023)53 extended the traditional mixed-layer eddy parameterization beyond the mixed-layer base by incorporating mixed transitional-layer instability, which is modulated by strain-induced frontogenesis. Our observational study highlights that the downscale energy transfers at fronts are ultimately associated with frontogenesis at the submesoscale. This finding advances our theoretical understanding of turbulent cascades in geophysical flows, and adds dissipation routes of oceanic kinetic energy with potentially profound consequences for the dissipation of mesoscale eddies, the evolution of the ocean’s general circulation, and climate change. It is likely that current state-of-the-art global ocean models may substantially understate the impacts of these frontogenetic processes, indicating instead a major inverse kinetic energy cascade at the submesoscale. Resolving submesoscale frontogenetic processes may require model resolution approaching O(100 m) in the horizontal20, which is particularly challenging for global ocean models due to their huge computational expense. Hence, future work is needed to both assess the large-scale effects of submesoscale frontogenesis, and develop a new parameterization for these effects in high-resolution regional ocean models, which can at least permit the key mechanisms responsible for the generation of horizontally convergent motions.

Methods

OSMOSIS data and processing

The data analyzed in this study were primarily collected from a mooring array deployed over the Porcupine Abyssal Plain (48.63∘-48.75∘N, 16.09∘-16.27∘W) in the northeast Atlantic (Fig. 1a), as part of the Ocean Surface Mixing, Ocean Submesoscale Interaction Study (OSMOSIS) experiment27,29,59. Nine sub-surface moorings were deployed for the period September 2012—September 2013, arranged in two concentric quadrilaterals with side lengths of  ~13 km (outer cluster) and 1–2 km (inner cluster) around a centrally located single mooring. Importantly, this configuration enabled simultaneous measurements of meso- and submesoscale properties. The observational site lies at the eastern edge of the North Atlantic gyre, a region of weak mean flow and moderate eddy kinetic energy that is arguably representative of a substantial fraction of the global ocean. Internal wave energy levels are also moderate and primarily contributed by semidiurnal internal tides, near-inertial waves, and the internal wave continuum60,61.

Mooring sensors comprised a series of paired MicroCAT conductivity-temperature-depth (CTD) sensors and acoustic current meters at different depths, spanning the approximate depth interval 30–530 m (Supplementary Fig. 1). Temperature, salinity and horizontal velocity measured by CTD and current meter instruments, with respective sampling intervals of 5 and 10 min, were interpolated onto a uniform depth grid (10 m intervals between depths of 50 m and 520 m) and averaged onto hourly intervals. A fourth-order low-pass Butterworth filter with a cut-off of 24 h (one inertial period is ~ 16 h) was then applied to the hourly data to remove unbalanced super-inertial motions. Note that internal diurnal tides cannot be generated nor propagate into the study region, and that barotropic diurnal tides are rather weak27,29. Further, the mooring measurements were complemented by hydrographic observations acquired by two ocean gliders that navigated in a bow-tie pattern across the mooring array for the entire sampling period46. The mixed-layer depth is calculated from coincident glider data using a threshold value of potential density increase (△ρ = 0.03 kg m−3) from a near-surface value at 10 m62.

Kinematic properties

Horizontal divergence, the vertical component of the relative vorticity, and strain rate can be calculated using spatial derivatives of velocity, \(\delta={\nabla }_{h}\cdot {{{{\bf{u}}}}}_{h}=\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}\), \(\zeta={{{\bf{k}}}}\cdot \nabla \times {{{\bf{u}}}}=\frac{\partial v}{\partial x}-\frac{\partial u}{\partial y}\), \(\alpha=\sqrt{{(\frac{\partial u}{\partial x}-\frac{\partial v}{\partial y})}^{2}+{(\frac{\partial v}{\partial x}+\frac{\partial u}{\partial y})}^{2}}\), where k is the vertical unit vector, ∇ is the spatial gradient operator, u  =  (u, v, w) is the 3 d velocity vector, the h subscript denotes horizontal component, and b = g(1 − ρ/ρ0) is buoyancy (with g denoting the gravitational acceleration, ρ the potential density, and ρ0 = 1025 kg m−3 the reference density).

The focus of this study is to examine the key factors in setting submesoscale frontogenesis and the associated energy transfers from the mooring observations. To this end, we quantify the rate of frontal sharpening using the frontogenetic rate13, defined as

$${T}_{b}={F}_{s}/| {\nabla }_{h}b{| }^{2},$$
(1)

where the frontogenesis function is Fs  =  Q  ⋅  ∇hb, with Q = (\(-\frac{\partial u}{\partial x}\frac{\partial b}{\partial x}-\frac{\partial v}{\partial x}\frac{\partial b}{\partial y}\), \(-\frac{\partial u}{\partial y}\frac{\partial b}{\partial x}-\frac{\partial v}{\partial y}\frac{\partial b}{\partial y}\)) denoting the so-called Q vector12.

The type of spatial arrangement used for the OSMOSIS array is rare in mooring deployments36,63,64, and makes this data set particularly well suited for quantifying the horizontal gradients of horizontal velocity and buoyancy (Fig. 2a–c). In this study, the analysis is performed using the full expanse of the mooring array (18 km) and mooring triplets (9 km and 2 km) to estimate the horizontal derivatives in velocity and buoyancy. The velocity and buoyancy measurements are taken at three corners for each triangle area, and then the horizontal derivatives can be calculated using the divergence theorem and the line integral around the triangle boundary. The water column in the shallow pycnocline during non-winter months exhibits super- and sub-inertial heaving, which produces overly large horizontal buoyancy gradients46; such signals are excluded here. All variables are normalized by the local Coriolis parameter \(f=2\Omega \sin \phi\), where Ω is the Earth’s angular velocity and ϕ the latitude.

Kinetic energy transfer

Our approach to quantifying cross-scale horizontal kinetic energy transfer, which refers to the exchange of kinetic energy across different flow scales, is based on the “coarse-graining” framework30,31. This technique involves calculating both the magnitude and direction (upscale or downscale) of nonlinear energy exchange from the quadratic terms in the equations of motion. This method is advantageous in comparison to the traditional spectral methods because it does not require windowing, nor the assumptions of homogeneity or isotropy65. Moreover, because the framework is Galilean invariant and employs filters in physical space, it can also provide structural information about the flow features where energy transfers occur. We define the energy transfer, Πω, as

$${\Pi }_{\omega }(t)=({\nabla }_{h}\overline{{{{{\boldsymbol{u}}}}}_{h\omega }}+{\nabla }_{h}{\overline{{{{{\boldsymbol{u}}}}}_{h\omega }}}^{T}):({\overline{({{{{\boldsymbol{u}}}}}_{h}{{{{\boldsymbol{u}}}}}_{h})}}_{\omega }-\overline{{{{{\boldsymbol{u}}}}}_{{h}_{\omega }}}\overline{{{{{\boldsymbol{u}}}}}_{{h}_{\omega }}}),$$
(2)

where t is time, uh denotes the vector of the total horizontal velocity, and uhω is the horizontal velocity component for frequencies lower (i.e. longer time scales) than a given value of ω, ∇h is a horizontal gradient, the superscript T denotes a transpose operator, and the colon is a tensor inner product. The result is a scalar that indicates the direction of energy transfer, with positive (negative) values denoting transfers to higher (lower) frequency.

From a mathematical perspective, the coarse-graining approach can be equivalently applied in both the wavenumber and frequency domains, as demonstrated by Naveira Garabato et al. (2022)27 and Srinivasan et al. (2023)20. One advantage of applying the coarse-graining approach in the frequency domain is that balanced submesoscale motions can be separated from unbalanced internal waves, whereas they are practically indistinguishable in the spatial domain.

Vertical velocity

The density conservation equation is used to determine vertical velocity, neglecting the diffusion term29,

$$\frac{D\rho }{Dt}=\frac{\partial \rho }{\partial t}+u\frac{\partial \rho }{\partial x}+v\frac{\partial \rho }{\partial y}+w\frac{\partial \rho }{\partial z}=0,$$
(3)

where \(\frac{D}{Dt}\) is the material derivative. The vertical velocity is estimated from the sum of a local isopycnal displacement term and a horizontal advection term, by rearranging equation (3) as

$$w=-\frac{\partial \rho }{\partial t}/\frac{\partial \rho }{\partial z}-\left(u\frac{\partial \rho }{\partial x}+v\frac{\partial \rho }{\partial y}\right)/\frac{\partial \rho }{\partial z}.$$
(4)

Vertical velocity in the mixed layer is not derived from the density conservation equation, as the neglected diffusion term becomes significant there. An alternative method for estimating vertical velocity is to apply the continuity equation under the assumption of zero vertical motion at the sea surface. However, measurements within the top 50 m were not conducted. To effectively apply the continuity equation, we would need detailed knowledge of the vertical distribution of horizontal divergence, or assume depth independence of horizontal divergence in the top 50 m. This assumption, however, is likely invalid according to Tarry et al. (2022)37.

Observational uncertainty in the horizontal divergence

We assess the uncertainties in the horizontal divergence diagnostics by addressing two main sources of error: mooring motion and instrumental inaccuracies in velocity measurements. First, the horizontal divergence estimates are based on horizontal gradients derived from velocity data collected by moorings. However, any undetected motion of the moorings can lead to uncertainty in the precise measurement locations. Stochastic models indicate that these horizontal displacements are typically < 500 m59. To incorporate this uncertainty, we model inter-mooring distance perturbations associated with mooring motion using time integration of a Gaussian white noise process with zero mean and non-zero variance, estimated from differential horizontal currents59. Second, there is instrumental error due to the limited precision of the sensors used in the moorings, which is an inherent constraint in the data collection process. According to the manufacturer’s specifications, Nortek Aquadopp current meters have an accuracy of 5  × 10−3 m s−1.

To quantify the total uncertainty arising from these two factors, we introduce random errors from both sources simultaneously and allow them to accumulate in the horizontal divergence estimates. We assume that the errors from mooring movement and instrumental noise are independent of each other. This procedure is repeated 10,000 times. Supplementary Fig. 7 illustrates the results, showing that the observational uncertainties considered here have only a minor impact. The horizontal divergence diagnostics remain qualitatively unchanged, while the quantitative effects of these uncertainties typically result in perturbations of < 0.025f, or ~ 10%.

Lastly, the vertical resolution of the velocity measurements is limited, and varies among different mooring clusters. The central mooring is the most heavily instrumented, with 13 current meters, while the inner and outer moorings have seven and five current meters, respectively. To assess the uncertainty arising from varying vertical resolution, we recalculated the horizontal divergence using vertically sub-sampled horizontal velocity data. Specifically, we reduced the vertical resolution of the central mooring by selecting seven and five current meters at approximately the same depths as those on the inner and outer moorings, corresponding to estimates at 2 km and 9 km, respectively. We found that our diagnostics are weakly sensitive to the vertical resolution of the data (Supplementary Fig. 8).

Statistical significance of the cross-scale kinetic energy transfer diagnostics

To determine the statistical significance of the diagnosed Πω from the observations, we conduct kinetic energy transfer calculations using synthetic horizontal velocity time series. These synthetic time series replicate the amplitudes of the observations but have randomized phases27. As a result, these synthetic time series are expected to exhibit, on average, no kinetic energy transfer, meaning that any non-zero transfers identified can be attributed to limited sampling. We treat this zero-transfer scenario as the null hypothesis and test the significance level at which it can be rejected using the actual time series data. Specifically, we evaluate the averaged kinetic energy transfer at fronts over the winter period. The observed values exceed the upper limit of the confidence interval across nearly the entire depth range, suggesting that the null hypothesis can be rejected with ~ 95% confidence (Supplementary Fig. 9). Consequently, we conclude that the downscale kinetic energy transfer diagnosed at fronts during winter is statistically significant.