Introduction

The collective modes of a many-body system fingerprint the symmetries underlying a phase of matter. They also play an important role in transitions to non-equilibrium states when the system is subjected to an external drive. Resonantly driving collective modes can lead to exotic wave propagation effects and, at strong driving, to instabilities leading to new symmetry-breaking non-equilibrium states1,2,3,4,5. An example for such an instability in classical physics is Faraday waves formed by parametrically driven surface waves6,7,8.

Accessing such phenomena in electronic systems is challenging due to a lack of methods for the control and manipulation of collective modes in solids. At the same time, realizing such control holds a lot of promise for applications in fields like plasmonics or spintronics. Here, we show that Floquet engineering, which employs driving at optical frequencies to manipulate electronic bandstructures9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38, can be an effective tool to control collective modes. We focus on plasmons in clean, two-dimensional materials which exhibit large quality factors due to the absence of impurity scattering and the suppression of Landau damping by the \(\sqrt{q}\) shape of their dispersion. We demonstrate that optical driving fields, far off-resonant relative to the plasmon frequencies, can lead to the formation of exceptional points and non-dispersive plasmonic states through a parametric coupling mechanism which we call “modulated Floquet parametric driving” (MFPD). For strong driving, we predict the existence of an emergent non-equilibrium state with spatio-temporal correlations that break time and space translation symmetry. This connects to the ongoing interest in using complex multi-component driving signals to control solid-state electrons38,39,40,41 and to induce non-equilibrium correlated states5,23,42,43,44,45,46,47,48. Furthermore we show that MFPD can be used to increase plasmon quality factors.

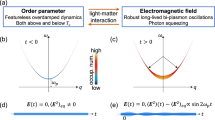
MFPD takes advantage of the fact that the electronic properties of two-dimensional materials are modified in the presence of high frequency time-periodic driving fields49. By slowly modulating the parameters of these fields, an electronic system can be controlled dynamically. As illustrated in Fig. 1a), a high-frequency Floquet driving alters the shape of the quasi-energy bands (red curves). In particular, the effective mass m* of electrons at the Fermi surface changes. This change results in an altered plasmon dispersion. A periodic modulation of the Floquet drive’s amplitude results in a periodically changing mass that parametrically excites plasmon modes. This effect induces two lines of exceptional points in the plasmon dispersion [Fig. 1b)]. These exceptional lines are separated by a non-dispersive gap where the real part of the plasmon dispersion is flat. Inside the gap, damping, which is reflected in the negative imaginary part of the plasmon dispersion, is reduced by MFPD. This effect can be used to enhance the quality of the plasmon resonance and increase plasmonic propagation lengths.

Fig. 1: Modulated Floquet parametric driving, exceptional lines and non-equilibrium steady states.
figure 1

a Illustration of the quasi-energy bands of electrons in a gapped system under MFPD. The dashed gray lines represent the undriven band structure. A Floquet signal with the frequency ΩF, where ℏΩF > Eg, is applied. The quasi-energy bands in the vicinity of the Fermi surface for a non-zero driving amplitude are shown in red. By modulating the amplitude of the fast Floquet drive with a frequency 2ω1, an oscillation of the dispersion and the effective mass of the electrons at the Fermi level is induced (see Eq. (6)). b The periodic modulation of the Fermi velocity induces two lines of exceptional points (shown as red circles) in the rotationally symmetric dispersion of the soft THz plasmon mode (green surfaces)—see Fig. 2 for an in-detail cross-sectional view. c) Above a critical value, the mass oscillation parametrically excites THz plasmons. Due to nonlinear and interaction effects, the plasmons arrange themselves in a crystal-like structure whose periodicity is determined by the condition \({\omega }_{1}={\omega }_{{{{{\rm{pl}}}}}}\left({q}^{*}\right)\), where \({\omega }_{{{{{\rm{pl}}}}}}\left(q\right)\) is the plasmon dispersion. The crystalline state breaks the rotational and translational symmetries of the undriven system and supports soft phonon-like Goldstone modes.

Full size image

For sufficiently strong driving, for plasmons with wavenumbers q* meeting the condition \({{{{\rm{Re}}}}}\left[{\omega }_{{{{{\rm{pl}}}}}}\left({q}^{*}\right)\right]={\omega }_{1}\), where \({\omega }_{{{{{\rm{pl}}}}}}\left(q\right)\) is the plasmon dispersion and 2ω1 is the amplitude modulation frequency, the imaginary part of the dispersion changes sign. These plasmons become unstable and, after a short period of exponential growth, form a crystal-like lattice with a periodically modulated electron density [Fig. 1c)]. The structure of this crystal is determined by the nonlinearities of the system. The density oscillates at half the modulation frequency, thus breaking the π/ω1 discrete time translation symmetry of the drive—a behavior known in discrete time crystals45,46,47,48,50,51,52,53,54.

An important challenge in Floquet engineered systems is heating55,56,57,58,59,60,61,62,63,64,65,66,67,68,69. Here, we show that the parametric excitation of plasmons by MFPD can be achieved in an off-resonant regime where (momentum conserving) single-photon excitation of electrons is blocked. To achieve this, the base-tone drive frequency ΩF and the Fermi energy μ must be chosen such that all electronic states supporting a resonant interband single-photon excitation with an energy transfer of ℏΩF and near-zero momentum transfer lie below the Fermi surface (see shaded regions Fig. 1). Processes involving multiple photons are suppressed in the small ratio of drive amplitude and drive frequency, leading to strongly reduced heating rates due to photoexcited electrons. We estimate the heating due to momentum non-conserving absorption mediated by phonons or impurity-scattering, as well as interaction-assisted processes, and find that the heating rates are small, such that they can be balanced by the cooling power of the crystal lattice.

Below, we describe in more detail the creation of singular plasmon dispersions and the excitation of plasmonic instabilities by MFPD, the transition into the crystalline state and the propagation of Goldstone-like, phononic collective modes in the symmetry broken state.

Results

Modulated Floquet parametric driving

The idea of MFPD is to use the dependence of the quasi-energy band structure on the parameters of the drive to couple to the soft collective modes of the system. We show how the slow modulation of the driving amplitude leads to a time-varying effective electron mass. For concreteness, let us consider a coherently driven, gapped 2D Dirac system described by the Hamiltonian

$$H=\sum\limits_{{{{{\bf{k}}}}}}{{{{{\bf{c}}}}}}_{{{{{\bf{k}}}}}}^{{{{\dagger}}} }\left[{H}_{0}\left({{{{\bf{k}}}}}\right)+{H}_{d}\left(t\right)\right]{{{{{\bf{c}}}}}}_{{{{{\bf{k}}}}}}+\sum\limits_{{{{{\bf{q}}}}}}V\left({{{{\bf{q}}}}}\right){\hat{\rho }}_{{{{{\bf{q}}}}}}{\hat{\rho }}_{-{{{{\bf{q}}}}}}.$$
(1)

We will first illustrate how the external drive modifies the dispersion in a single valley. The dispersion in the opposite valley is modified similarly. Both valleys will be taken into account when considering the collective modes. For small values of k around the center of the valley, we have H0 = d ⋅ σ, where \({{{{\bf{d}}}}}=\left[\lambda {k}_{x},\lambda {k}_{y},{E}_{g}/2\right]\), σ is a Pauli matrix vector describing the orbital pseudospin degree of freedom and Eg is the energy gap between the two bands. \({{{{{\bf{c}}}}}}_{{{{{\bf{k}}}}}}^{{{{\dagger}}} }\) (ck) are two-component electron creation (annihilation) operators, where individual components describe electrons with different pseudospin orientations, and \({H}_{d}\left(t\right)=e{{{{\bf{A}}}}}\left(t\right)\cdot {\nabla }_{{{{{\bf{k}}}}}}{H}_{0}\) is the driving Hamiltonian derived from minimal coupling.

We assume circularly polarized light with an amplitude \({{{{\mathcal{E}}}}}\) described by \({{{{\bf{A}}}}}\left(t\right)=\left({{{{\mathcal{E}}}}}/{\Omega }_{F}\right)\left[-\sin {\Omega }_{F}t,\cos {\Omega }_{F}t,0\right]\). The 2D Fourier transform of the Coulomb potential is given by \(V\left({{{{\bf{q}}}}}\right)=2\pi /q\) and \({\hat{\rho }}_{{{{{\bf{q}}}}}}={\sum }_{{{{{\bf{k}}}}}}{{{{{\bf{c}}}}}}_{{{{{\bf{k}}}}}}^{{{{\dagger}}} }{{{{{\bf{c}}}}}}_{{{{{\bf{k}}}}}+{{{{\bf{q}}}}}}\) is the density operator. We emphasize that we use the gapped Dirac Hamiltonian of Eq. (1) as an example. The physics presented here does not depend on the precise band structure of the system.

It is convenient to work in a rotating frame defined by the unitary transformation \(U\left(t\right)={e}^{i\hat{{{{{\bf{d}}}}}}\cdot {{{{\boldsymbol{\sigma }}}}}{\Omega }_{F}t/2}\), where the spectrum of the transformed single-particle part of Eq. (1) is given by

$${\varepsilon }_{k}\approx \sqrt{{\left(\left\vert {{{{\bf{d}}}}}\right\vert -\hslash \frac{{\Omega }_{F}}{2}\right)}^{2}+\frac{{e}^{2}{{{{{\mathcal{E}}}}}}^{2}{\lambda }^{2}}{4{\Omega }_{F}^{2}{\hslash }^{2}}\left(2-\frac{{E}_{g}}{\left\vert {{{{\bf{d}}}}}\right\vert }\right)}$$
(2)

for \(\lambda k/\left\vert {{{{\bf{d}}}}}\right\vert \ll 1\). In writing Eq. (2) we neglected time-dependent terms in the rotating frame11. In this frame and with the approximations made, the time dependence caused by the fast ΩF oscillation of the Floquet drive does not explicitly appear in the equations.

We consider the metallic regime with the Fermi surface lying in the upper band (see Fig. 1) and expand the spectrum around kF – the Fermi momentum of the undriven system. We write:

$${\varepsilon }_{k}\approx \hslash {v}_{F}\left({{{{\mathcal{E}}}}},{\Omega }_{F}\right)\left(k-{k}_{F}\right)+{\varepsilon }_{{k}_{F}}\left({{{{\mathcal{E}}}}},{\Omega }_{F}\right).$$
(3)

The Fermi velocity \({v}_{F}\left({{{{\mathcal{E}}}}},{\Omega }_{F}\right)\) depends on the amplitude and frequency of the Floquet drive.

A variation of the drive amplitude \({{{{\mathcal{E}}}}}\) results in a small change of the dispersion \({\varepsilon }_{k}\to {\bar{\varepsilon }}_{k}+\delta {\varepsilon }_{k}\) near the Fermi surface. To clearly distinguish between constant quantities and quantities oscillating with the slow modulation frequency ω1, here and in the following, we write the constant part with a bar. The total charge of the system is conserved and therefore kF is fixed. However, the slope of εk at kF and therefore the effective mass of the electrons \({m}^{*}=\hslash {k}_{F}/{v}_{F}\left({{{{\mathcal{E}}}}},{\Omega }_{F}\right)\) are altered. For a small δεk, we find

$${\bar{\varepsilon }}_{k}+\delta {\varepsilon }_{k}\approx \left(1-\frac{\delta {m}^{ * }}{{\bar{m}}^{ * }}\right)\frac{{\hslash }^{2}{k}_{F}}{{\bar{m}}^{ * }}\left(k-{k}_{F}\right).$$
(4)

We consider a slow, adiabatic oscillation of the electric field amplitude \({{{{\mathcal{E}}}}}\),

$${{{{\mathcal{E}}}}}\left(t\right)=\bar{{{{{\mathcal{E}}}}}}+\delta {{{{\mathcal{E}}}}}\cos \left(2{\omega }_{1}t\right),$$
(5)

such that ω1 ≪ ΩF. This slow oscillation does not couple to any single-electron degrees of freedom. However, as demonstrated below, it does couple to the soft plasmon mode through a parametric resonance induced by the periodic change of the effective mass

$${m}^{ * }\left(t\right)={\bar{m}}^{ * }\left(1+\frac{\delta {m}^{ * }\left(t\right)}{{\bar{m}}^{ * }}\right).$$
(6)

Equations of motion for collective dynamics

To describe the electron dynamics of MFPD-driven plasmons, we use a hydrodynamic description of Coulomb interacting electrons (see, e.g., refs. 70,71,72). The equations of motion follow from the conservation of charge and momentum73,74,75. The continuity equation for the electron density ρ is

$${\partial }_{t}\rho \left(t,{{{{\bf{x}}}}}\right)=-{\partial }_{i}\left[\rho \left(t,{{{{\bf{x}}}}}\right){u}_{i}\left(t,{{{{\bf{x}}}}}\right)\right],$$
(7)

where \({{{{\bf{u}}}}}\left(t,{{{{\bf{x}}}}}\right)\) is the electron flow velocity. The continuity equation for the momentum density is given by the Euler equation

$${\partial }_{t}\left({m}^{ * }\rho {u}_{i}\right)+{\partial }_{j}{\Pi }_{ij}=-\gamma {m}^{ * }\rho {u}_{i}-e\rho {\partial }_{i}\phi,$$
(8)

where m* = ℏkF/vF is the effective mass of electrons at the Fermi surface, given by the ratio of Fermi momentum ℏkF and Fermi velocity vF, ui is the electron flow velocity, and γ is the rate of momentum relaxation, e.g., due to impurity or phonon scattering. The stress tensor Πij is given by

$${\Pi }_{ij}={m}^{ * }\rho {u}_{i}{u}_{j}+{\delta }_{ij}p,$$
(9)

where p is the pressure. The electrostatic potential is given by

$$\phi \left(t,{{{{\bf{x}}}}}\right)=\int\,{d}^{2}{x}^{{\prime} }\frac{e\rho \left(t,{{{{{\bf{x}}}}}}^{{\prime} }\right)}{4\pi \varepsilon \left\vert {{{{\bf{x}}}}}-{{{{{\bf{x}}}}}}^{{\prime} }\right\vert }.$$
(10)

Here e is the electron charge and ε is the effective dielectric constant. Solutions of equations (7) and (8) describe the collective oscillations of the electron fluid.

Oscillating mass

The oscillating mass increment \(\delta {m}^{*}\left(t\right)\) in Eq. (8) acts as a parametric drive, which is known to lead to instabilities76. In the following we identify the parametric instability of the charge density ρ. It is convenient to take the divergence of Eq. (8) and to combine the result with the continuity equation (7), including the drive-induced temporal modulation of \({m}^{*}\left(t\right)\). Doing so, we find

$${\partial }_{t}{m}^{ * }\left(t\right){\partial }_{t}\rho+\gamma {m}^{ * }\left(t\right){\partial }_{t}\rho -{m}^{ * }\left(t\right){\partial }_{i}{\partial }_{j}\rho {u}_{i}{u}_{j}={\partial }_{i}\rho {\partial }_{i}\phi,$$
(11)

where we neglected the pressure term p since its contribution is subleading to the long-range Coulomb potential77,78 (The Fourier transform of the Coulomb potential is \(V\left(q\right)=2\pi /q\) and is responsible for the characteristic \(\sim \sqrt{q}\) dispersion of two dimensional plasmons, whereas the pressure term scales as  ~ q and will only contribute a small correction). Unless otherwise indicated, throughout the paper, derivatives act on all functions to the right. In our derivations, we also neglect the time-dependent contribution to the damping term, which is negligible in comparison to the static one.

Instabilities and exceptional points

In this section, we present how the oscillating mass under MFPD in Eq.(6) influences the plasmon dynamics under Eq. (11). Consider the electron density \(\rho=\bar{\rho }+\delta \rho\), where \(\bar{\rho }\) is the equilibrium electron density and δρ is a perturbation of \(\bar{\rho }\). To linear order in δρ, and performing a Fourier transform x → q, for a modulation \(\delta {m}^{*}\left(t\right)/{\bar{m}}^{*}=h\cos \left(2{\omega }_{1}t\right)\), we obtain from Eq. (11)

$${\partial }_{t}\left(1+h\cos \left(2{\omega }_{1}t\right)\right){\partial }_{t}\delta {\rho }_{q}+\gamma {\partial }_{t}\delta {\rho }_{q}+{\omega }_{{{{{\rm{pl}}}}}}^{2}\left(q\right)\delta {\rho }_{q}=0.$$
(12)

The plasmon dispersion is given by

$${\omega }_{{{{{\rm{pl}}}}}}\left(q\right)=\sqrt{\frac{e\bar{\rho }}{4\pi {\bar{m}}^{ * }\varepsilon }{q}^{2}V\left(q\right)}.$$
(13)

The parameter γ captures scattering on impurities and lattice excitations, which lead to damping of the plasmon modes. Intrinsic Landau damping is strongly suppressed for the wavenumbers and frequencies under consideration, since they lie outside of the particle-hole continuum. Indeed, recent experiments on high quality graphene showed that damping mainly arises due to scattering with phonons79. It is important to note that this scattering mechanism is strongly suppressed at low temperatures, where dissipation is dominated by losses caused by electric fields penetrating into the substrate79. In general, it is believed that substrate engineering and strong cooling could strongly increase the plasmon quality80. Notice that Eq. (12) is equivalent to the equation describing the propagation of the magnetic field in photonic time crystals81.

In the section “Slowly varying envelope approximation,” we derive a solution for δρq using the slowly varying envelope approximation, which is valid near the parametric resonance where \({\omega }_{{{{{\rm{pl}}}}}}^{2}\left(q\right)\approx {\omega }_{1}^{2}\):

$$\delta {\rho }_{q}\left(t\right)={a}_{q}\left(t\right)\cos \left({\omega }_{1}t\right)+{b}_{q}\left(t\right)\sin \left({\omega }_{1}t\right).$$
(14)

Here the amplitudes are given by \({a}_{q}\left(t\right)={a}_{q}\left(0\right){e}^{{s}_{\pm }\left(q\right)t}\) and \({b}_{q}\left(t\right)={b}_{q}\left(0\right){e}^{{s}_{\pm }\left(q\right)t}\), where

$${s}_{\pm }\left(q\right)=-\frac{\gamma }{2}\mp \, i\frac{{\omega }_{1}}{2}\sqrt{\frac{{\left[{\omega }_{{{{{\rm{pl}}}}}}^{2}\left(q\right)-{\omega }_{1}^{2}\right]}^{2}}{{\omega }_{1}^{4}}-{\left(\frac{h}{2}\right)}^{2}}.$$
(15)

We now examine the plasmon dispersion in the presence of parametric driving. To this end, it is convenient to rewrite Eq. (14): according to Floquet’s theorem, any solution to Eq. (12) can be written in the form \(\delta {\rho }_{q}={e}^{-i\Lambda \left(q\right)t}{u}_{\Lambda }\left(t\right)\), where \({u}_{\Lambda }\left(t+\pi /{\omega }_{1}\right)={u}_{\Lambda }\left(t\right)\). Choosing \({u}_{\Lambda }\left(t\right)=\left[{a}_{{\Lambda }_{\pm }\left(q\right)}\left({e}^{2i{\omega }_{1}t}+1\right)-i{b}_{{\Lambda }_{\pm }\left(q\right)}\left({e}^{2i{\omega }_{1}t}-1\right)\right]/2\), and comparing to Eq. (14), we obtain a correspondence between \(\Lambda \left(q\right)\) and s\(\left(q\right)\) giving the plasmon dispersion close to the resonance:

$${\Lambda }_{\pm }\left(q\right)=i{s}_{\pm }\left(q\right)+{\omega }_{1}.$$
(16)

Note that the Floquet exponent \(\Lambda \left(q\right)\) is defined modulo 2ω1 (because a change by 2ω1 can always be absorbed into \({u}_{\Lambda }\left(t\right)\)). In analogy to the Bloch theory of electronic band structure, 2ω1 plays the role of a reciprocal lattice vector.

While Eqs. (15) and (16) are valid near \({\omega }_{{{{{\rm{pl}}}}}}\left(q\right)={\omega }_{1}\), for small q, keeping higher order derivatives neglected above in the slowly varying envelope approximation, and ignoring damping, we find that the two branches of the plasmon dispersion are given by \({\Lambda }_{+}\left(q\right)\approx 2{\omega }_{1}-{\omega }_{{{{{\rm{pl}}}}}}\left(q\right)/\sqrt{1+{h}^{2}/4}\) and \({\Lambda }_{-}\left(q\right)\approx {\omega }_{{{{{\rm{pl}}}}}}\left(q\right)/\sqrt{1+{h}^{2}/4}\). For the Λ− branch, we find \({b}_{{\Lambda }_{-}\left(q=0\right)}=i{a}_{{\Lambda }_{-}\left(q=0\right)}\), giving \(\delta {\rho }_{q}\approx {a}_{{\Lambda }_{-}\left(q=0\right)}{e}^{i{\omega }_{{{{{\rm{pl}}}}}}\left(q\right)t/\sqrt{1+{h}^{2}/4}}\). Therefore, the Λ− branch describes a counter-propagating mode with the frequency \(-i{\omega }_{{{{{\rm{pl}}}}}}\left(q\right)/\sqrt{1+{h}^{2}/4}\), lifted by one reciprocal lattice vector 2ω1. We conclude that, away from the resonance, the parametric driving influences the plasmons only weakly. The plasmon dispersion in the presence of parametric diving \(\Lambda \left(q\right)\) is shown in Fig. 2.

Fig. 2: Onset of the plasmon instability induced by modulated Floquet parametric driving with the modulation frequency 2ω1. Exceptional points.
figure 2

Red and blue lines show the the quasi-energy dispersion \({{{{\rm{Re}}}}}\left[\Lambda \left(q\right)\right]\) of parametrically driven plasmons (see Eq. (16) and discussion below). Far away from the critical q*, 2D plasmons retain the characteristic square-root shape of their dispersion relation (blue lines). The quasi-energy dispersion is invariant with respect to shifts by 2ω1—the reciprocal lattice constant in frequency space. Near q*, where \({\omega }_{{{{{\rm{pl}}}}}}\left({q}^{*}\right)\approx {\omega }_{1}\) holds, the dispersion is strongly altered by the driving (red lines). A gap which hosts non-dispersive modes opens around q* (yellow shading). Merging branches of the dispersion at the edges of the non-dispersive gap indicate exceptional points with diverging group velocities. We chose the modulation amplitude h to lie slightly above the instability threshold: damping is negative in a small interval around q*, leading to an exponential growth of unstable modes (red shading). However, exceptional points and non-dispersive states appear even for subcritical driving strengths.

Full size image

Exceptional points appear at wavenumbers qexc, where the  ± -branches of \({s}_{\pm }\left(q\right)\) merge, i.e., when the condition \({\omega }_{{{{{\rm{pl}}}}}}^{2}\left({q}_{{{{{\rm{exc}}}}}}\right)={\omega }_{1}^{2}\left(1\pm h/2\right)\) is met. This results in a diverging group velocity \(\partial {s}_{\pm }\left(q\right)/\partial q \sim {\left\vert q-{q}_{{{{{\rm{exc}}}}}}\right\vert }^{-1/2}\) for q → qexc. In the interval between the two exceptional points qexc, \({s}_{\pm }\left(q\right)\) is purely real. This corresponds to non-dispersive plasmons, oscillating at frequency ω1 (see Fig. 2).

Let us now consider the stability of plasmon modes under MFPD. The instability condition \({{{{\rm{Re}}}}}\left(s\right) > 0\) is realized for h > 2γ/ω1 in a narrow frequency range around \({\omega }_{{{{{\rm{pl}}}}}}\left(q\right)={\omega }_{1}\) given by

$${\left[{\omega }_{{{{{\rm{pl}}}}}}^{2}\left(q\right)-{\omega }_{1}^{2}\right]}^{2} < \ {\omega }_{1}^{4}{h}^{2}/4-{\omega }_{1}^{2}{\gamma }^{2}.$$
(17)

The fastest growing modes have wavenumbers q* determined by the condition

$$\pm {\omega }_{{{{{\rm{pl}}}}}}\left({q}^{ * }\right)={\omega }_{1}.$$
(18)

Thus, the parametric driving will excite plasmons with the frequency ω1, whose amplitude will grow according to \({\delta \rho }_{{q}^{*}} \sim {e}^{\left(h{\omega }_{1}/4-\gamma /2\right)t}\). Notice that the system’s response breaks the discrete time translation symmetry of the drive with respect to translations by T = π/ω1.

The periodic driving opens a vertical non-dispersive gap around q*, where the two branches of the plasmon dispersion meet. Inside the gap, the real part of \({\Lambda }_{\pm }\left(q\right)\) is flat. This phenomenon is known from photonic time-varying media and photonic time crystals, where it is often referred to as momentum-gap or k-gap81,82. In fact, Eq. (12) maps onto the equation describing the propagation of light through a photonic time crystal81. The full plasmon dispersion near the onset of the instability (hω1/4 ≳ γ/2) is illustrated in Fig. 2.

Enhancing plasmonic quality factors

In this section, we show how MFPD below the instability threshold can be used to enhance plasmonic quality factors. As an example we consider a plasmon source that is located at x = 0 and is, for simplicity, uniform along the y-axis, which is a reasonable approximation for a strip whose width is shorter than the plasmon wavelength83. This source is placed into an MFPD-driven plasmonic medium. We use Eq. (12) with a pointlike source term oscillating at frequency ω1 added to the left-hand side to analyze plasmon propagation in this setting. In the Supplementary Information, we show that for any fixed t → ∞, the plasmon amplitude away from the source behaves as

$$\delta \rho \left(x\right) \sim \delta \rho \left(0\right){e}^{-\frac{{q}^{*}}{{{{{\mathcal{Q}}}}}\left(h\right)}\left\vert x\right\vert },$$
(19)

where

$${{{{\mathcal{Q}}}}}\left(h\right)=\frac{1}{\sqrt{{\gamma }^{2}/{\omega }_{1}^{2}-{h}^{2}/4}}$$
(20)

is the plasmon quality factor. In the absence of MFPD, \({{{{\mathcal{Q}}}}}\left(h\right)\) reduces to the well known expression \({{{{\mathcal{Q}}}}}\left(h=0\right)={\omega }_{1}/\gamma\). Eq. (20), shows that for driving strengths h close to, but below the instability threshold hc = 2γ/ω1, the quality of the plasmon resonance can be strongly enhanced. To demonstrate the enhancement, we perform a numerical simulation of Eq. (12). For all simulations in this paper we use the Dedalus spectral solver84. The results (see Fig. 3) show a good agreement with Eq. (19), and demonstrate that a significant enhancement of \({{{{\mathcal{Q}}}}}\) can be achieved at driving strengths below the instability threshold. This opens the possibility of enhancing the quality of plasmon resonances with high-frequency optical drives.

Fig. 3: Enhancement of the plasmon quality factor by MFPD.
figure 3

A source at x = 0 induces plasmons propagating along the x-axis. The plasmon amplitude is exponentially damped according to Eq. (19). Blue and green curves show the plasmon wave with MFPD switched on and off, respectively. The enhancement of the plasmon quality factor shows in a larger propagation length and agrees well with the prediction of Eq. (20). A driving strength of h = 0.75hc was used in the simulation.

Full size image

Finally, we note that the quality factor \({{{{\mathcal{Q}}}}}\) depends on temperature. In experiments with graphene plasmons, \({{{{\mathcal{Q}}}}}\) roughly decreases by a factor of two when the temperature is raised from 100 K to 200 K79. Below, we estimate that the temperature raise induced by MFPD is on the order of a few tens of Kelvin for h = hc. Thus MFPD can compensate for the heating-induced lowering of \({{{{\mathcal{Q}}}}}\), if h is chosen close to hc.

Crystallization

We now turn to describing pattern formation that occurs for MFPD above the critical driving threshold, h > hc. Having identified the wavenumber q* of the unstable modes in Eqs. (13) and (18), we now study the steady state spatial structure of the plasmon charge density once the initial exponential growth has been saturated by the nonlinearities. We use the nonlinear equation of motion for plasmons with an oscillating mass term, Eq. (11), derived in the section “Oscillating mass.” For simplicity, we focus on a quasi-1D strip whose width along the y-direction is smaller than the plasmon wavelength λ* = 2π/q*. These boundary conditions are implemented by setting ρ = 0 outside the strip.

Parametrically driven nonlinear waves were thoroughly studied in nonlinear spin and optical systems in the context of wave turbulence85. In general, the saturation of unstable modes can be described within the subspace of modes that satisfy the condition \(2{\omega }_{1}={\omega }_{{{{{\rm{pl}}}}}}\left(q\right)+{\omega }_{{{{{\rm{pl}}}}}}\left(-q\right)\)85. For the strip geometry, where qy is fixed to zero, these are precisely the linearly unstable modes of Eqs. (14) and (34). Physically, the above condition reflects that the uniform parametric driving cannot supply momentum to the system, and plasmons can only be created in pairs with wavenumbers qx = ± q*. Thus, the saturation to the final steady state will be captured by the ansatz

$$\begin{array}{rcl}\delta {\rho }_{s}\left(t,y\right)&=&a\left(t\right)\cos \left({\omega }_{1}t\right)\cos \left({q}^{*}\cdot x\right)\\ &&+b\left(t\right)\sin \left({\omega }_{1}t\right)\cos \left({q}^{*}\cdot x\right).\end{array}$$
(21)

A similar instability appears in parametrically driven shallow water waves, so called Faraday waves6,7,8,86,87,88,89. The Faraday instability has also been reported for cold atom systems90,91 and Luttinger liquids92.

As shown in the sec “Analysis of nonlinear pattern formation” inserting the ansatz of Eq. (21) into the plasmon equation of motion (11) leads to the set of amplitude equations

$$\begin{array}{l}\dot{a}=-\alpha b-\frac{1}{2}\gamma a+\beta b\left({a}^{2}+{b}^{2}\right)\\ \dot{b}=-\alpha a-\frac{1}{2}\gamma b-\beta a\left({a}^{2}+{b}^{2}\right),\end{array}$$
(22)

with α = ω1h/4 and \(\beta={\omega }_{1}/32{\left(\bar{\rho }\right)}^{2}\). To gain an intuition for the steady state, it is useful to consider the fixed point, where \(\dot{a}\left({a}_{{{{{\rm{fp}}}}}},{b}_{{{{{\rm{fp}}}}}}\right)=\dot{b}\left({a}_{{{{{\rm{fp}}}}}},{b}_{{{{{\rm{fp}}}}}}\right)=0\) and solve for the amplitude \({r}_{{{{{\rm{fp}}}}}}^{2}={a}_{{{{{\rm{fp}}}}}}^{2}+{b}_{{{{{\rm{fp}}}}}}^{2}\). Here, the subscript “fp” stands for values at the fixed point. One finds

$${r}_{{{{{\rm{fp}}}}}}^{2}={a}_{{{{{\rm{fp}}}}}}^{2}+{b}_{{{{{\rm{fp}}}}}}^{2}=\frac{\alpha }{\beta }\sqrt{\left[1-{\left(\frac{\gamma }{2\alpha }\right)}^{2}\right]}.$$
(23)

This expression indicates a critical point at hc = 2γ/ω1, beyond which, for h > hc, physically meaningful fixed points with a real, finite amplitude rfp exist. Equation (23), also shows that the amplitude rfp has two distinct scaling regimes connected by a crossover. For large h, the damping γ is negligible and \({r}_{{{{{\rm{fp}}}}}}\approx \sqrt{\alpha /\beta }\). On the other hand, close to the critical point hc, we find \({r}_{{{{{\rm{fp}}}}}}\approx \sqrt{{\alpha }_{c}/\beta }{\left(2\epsilon \right)}^{1/4}\), where \(\epsilon=\left(\alpha -{\alpha }_{c}\right)/{\alpha }_{c}\) with α = ω1hc/4. We will refer to these two cases as the weakly damped and the strongly damped, respectively. In what follows, we use Eqs. (22) to study the transition to the crystalline non-equilibrium steady state in both cases.

We begin with the weakly damped case. For γ = 0 Eqs. (22) correspond to the equations of motion arising from the Hamiltonian

$$H\left(a,b\right)=\frac{1}{2}\alpha \left({a}^{2}-{b}^{2}\right)+\frac{1}{4}\beta \left({a}^{4}+{b}^{4}\right)+\frac{1}{2}\beta {a}^{2}{b}^{2}.$$
(24)

Similar Hamiltonians are obtained for nonlinear parametric oscillators in both quantum and classical limits93,94. The stable minima of the Hamiltonian (24) are located at:

$${a}_{*}=0,\,{b}_{*}=\pm \sqrt{\frac{\alpha }{\beta }},$$
(25)

In the presence of weak damping, Eqs. (22) predict that, for any initial condition, the trajectory \(r\left(t\right)=\left(a\left(t\right),b\left(t\right)\right)\) will descend to one of the minima predicted by Eq. (25) (see Fig. 4). The steady state will be a standing wave of the form of Eq. (21) with the amplitude given by Eq. (25).

Fig. 4: Effective Hamiltonian for the weakly damped case.
figure 4

The effective Hamiltonian of Eq. (24) in amplitude space is shown, with the two minima corresponding to symmetry-breaking states. The red trajectory is a solution to Eqs. (22) and shows the transition to the crystalline state in the presence of weak damping.

Full size image

We note that noise can significantly alter the dynamics of the plasmon modes. It can, e.g., lead to transitions between the two minima of the Hamiltonian (24)93. In the case of multiple non-degenerate minima, noise can determine the ultimate stable configuration93.

Next, we address the strongly damped case where h is only slightly above the instability threshold hc = 2γ/ω1. Expanding Eqs. (22) in \(\epsilon=\left(h-{h}_{c}\right)/{h}_{c}\) (see Supplementary Information), we find that \(a\left(t\right)\approx -b\left(t\right)\) and the time dependence of the mode amplitudes is – to first order in ϵ – captured by the equation \(\dot{d}=-\partial V\left(d\right)/\partial d\), where d = a − b and the potential \(V\left(d\right)\) is given by

$$V\left(d\right)=-\epsilon \frac{{\alpha }_{c}}{2}{d}^{2}+\frac{{\beta }^{2}}{48{\alpha }_{c}}{d}^{6}.$$
(26)

The equation for \(\dot{d}\) describes a gradient descent dynamics towards one of the two minima of the potential (26). We plot the effective potential for different values of ϵ in Fig. 5 and conclude that the transition into the symmetry breaking state is continuous, i.e., the system goes through a soft bifurcation when h reaches the critical driving strength hc. In terms of the original a and b, the potential minima [and approximate fixed points of Eqs. (22)] are located at

$$a=-b=\pm \sqrt{\frac{{\alpha }_{c}}{\beta }}{\left(\epsilon /2\right)}^{1/4}.$$
(27)
Fig. 5: Effective potential for the strongly damped case.
figure 5

The potential \(V\left(d\right)\) of Eq. (26) with the two minima corresponding to symmetry-breaking steady states of the driven systems. The system undergoes a continuous symmetry breaking transition when driven above the threshold value hc = 2γ/ω1, i.e. when ϵ = h/hc − 1 > 0.

Full size image

After studying plasmon pattern formation in 1D, we extend our results to two dimensions, focusing on a driving strength slightly above the instability threshold. In two dimensions, the condition \(2{\omega }_{1}={\omega }_{{{{{\rm{pl}}}}}}\left(q\right)+{\omega }_{{{{{\rm{pl}}}}}}\left(-q\right)\) for selecting modes that contribute to the steady-state solution does not specify a finite set of modes. Instead, all modes with wavevectors q* that satisfy \(\left\vert {{{{{\bf{q}}}}}}^{*}\right\vert={q}^{*}\) can, in principle, contribute. Studies of pattern formation in Faraday waves87,88,89 suggest that a finite number of modes N with wavevectors \({{{{{\bf{q}}}}}}_{i}^{*}\) will be selected, such that the angle between the wavevectors is given by π/N. While for N = 1, one obtains a standing wave, the N = 2 case corresponds to a square tiling and the N = 3 case gives a hexagonal or triangular tiling. To find the plasmon pattern to which the system converges in the steady state, we performed numerical simulations of Eqs. (7)-(8) under MFPD (for details we refer to the Supplementary Information). As a closest feasible approximation to an infinite plane, we choose a periodic domain with side length commensurate with the plasmon wavelength λ* = 2π/q*. Curiously, the patterns quickly reach states with complex, quasiperiodic patterns of waves with wavelengths λ*, then slowly settle on a nearly square pattern after a series of transformations. A typical cristallization process is shown in Fig. 6.

Fig. 6: Plasmonic pattern formation under MFPD in two dimensions in the strongly damped regime.
figure 6

The plots show a numerical solution of Eqs. (7)-(10). Commensurate periodic boundary conditions were used in both directions. The driving and damping parameters used in this plot are h = 0.05, γ = 0.045ω1. Initial patterns with a characteristic periodicity of λ* = 2π/q* quickly form from the random initial conditions. The final stable square pattern is reached after a series of transformations. Time is given in units of T = π/ω1.

Full size image

We find that, generally, plasmons arrange themselves in square patterns in the steady state. This is even true for square domains incommensurate with λ*. We note that the observed patterns are not perfect square tilings. This is due to the presence of small amplitude modes with larger wavenumbers caused by the nonlinearities (see Supplementary Information). By fine tuning the boundary conditions, we were also able to realize a triangular pattern (see Supplementary Information). We also note that, under experimental conditions, noise can influence the steady state to which the system finally settles93. Our conclusion is that while a square tiling is preferred generally, boundary conditions can affect the final pattern.

Goldstone-like phonons

The crystalline steady state breaks the translational symmetry of the system. We show here that this breaking of a continuous symmetry manifests itself in the presence of Goldstone-like phonon modes. We focus on the strip geometry.

Above, we found the steady state solution: \(\delta \rho=\pm \sqrt{\alpha /\beta }\sin \left({\omega }_{1}t\right)\cos \left({q}^{ * }x\right)\) [see Eqs. (21) and (25)] for the weakly damped case, which we will consider in this section. This solution remains valid if we shift the phase of the spatial part by φ:

$$\delta \rho=\pm \sqrt{\frac{\alpha }{\beta }}\sin \left({\omega }_{1}t\right)\cos \left({q}^{*}x+\varphi \right).$$
(28)

If homogeneous and static, the phase shift can always be eliminated by the coordinate transformation x → x − φ/q*. However, if the phase shift is spatially dependent, Eq. (11) determines its dynamics. Thus, we investigate the dynamics of \(\varphi \left(t,x\right)\), via the ansatz \(\delta \rho=\pm \sqrt{\alpha /\beta }\sin \left({\omega }_{1}t\right)\cos \left[{q}^{*}x+\varphi \left(t,x\right)\right]\), which remains an approximate solution to Eq. (11). Since a uniform ϕ has no influence on the dynamics of the system, we expect slow dynamics for a long wavelength spatial dependence of \(\varphi \left(t,x\right)\), i.e., we expect Goldstone-like modes.

In the section “Deriving the Goldstone modes” we find that the dynamics of \(\varphi \left(t,x\right)\) is governed by a wave equation that, to linear order, is solved by plane waves \(\varphi \left(t,x\right)={{{{\rm{Re}}}}}\left[{e}^{-i{\Omega }_{\pm }\left(Q\right)t+iQx}\right]\) with the dispersion:

$${\Omega }_{\pm }\left(Q\right)\approx \pm \frac{{\omega }_{1}}{{q}^{*}}\sqrt{\left(1+3h\right)}Q.$$
(29)

We note that similar modes have been observed experimentally in parametrically driven classical liquids95. Interestingly, the dispersion (29) is linear, unlike the plasmon plasmon dispersion \({\omega }_{{{{{\rm{pl}}}}}}\left(q\right)\). On long scales, the lattice distortions are net-neutral, therefore lacking a long-range restoring force.

Besides the Goldstone modes, the symmetry breaking state supports optical modes. These correspond to oscillations of the amplitudes a, b in Eq. (22).

To derive the dispersion of the optical modes, we expand the effective Hamiltonian in Eq. (24) around the minimum at a = 0, \(b=\sqrt{\alpha /\beta }\):

$$H\approx -\frac{{\alpha }^{2}}{4\beta }+\alpha \left(\delta {b}^{2}+\delta {a}^{2}\right).$$
(30)

The corresponding Hamilton’s equations read

$$\begin{array}{rcl}\delta \dot{b}&=&2\alpha \delta a\\ \delta \dot{a}&=&-2\alpha \delta b,\end{array}$$
(31)

and are solved by a uniform oscillation of the amplitudes with the frequency 2α:

$$\delta \ddot{a}+4{\alpha }^{2}\delta a=0,$$
(32)

with α = ω1h/4.

The collective modes of the symmetry broken state described by Eqs. (29) and (32) are one possible experimental signature of the crystalline state. When the dissipation rate γ is included, the modes will obtain a negative imaginary part  ~ − iγ, broadening the resonances.

Heating and Landau damping

Coherent driving of interacting systems leads to heating55,56,57,58,59,60,61,62,63,64,65,66,67,68,69. This can be a problem, as high temperatures can interfere with the studied effects, or even damage the systems. As described above, MFPD operates in a regime where two major sources for heating in Floquet-engineered systems—radiative recombination and momentum conserving single photon absorption23,65—are suppressed by the Pauli exclusion principle. Here we investigate heating due to other relevant processes, in particular disorder and phonon-assisted single-photon absorption and interaction-assisted single-photon absorption.

In the first process, a single electron absorbs the energy ℏΩF and is scattered by a phonon, a defect, or an impurity. In our theory, the rate of momentum relaxation is given by γ (see Eq. (8)), which captures a variety of momentum-relaxing microscopic processes. We use γ, which is related to the quality factor \({{{{\mathcal{Q}}}}}\), to estimate the rate of momentum non-conserving photon absorption. In the second process, the energy of a photon is distributed between two interacting electrons. This latter process is strongly suppressed by the available phase-space, constrained by energy-momentum conservation. The derivation of our estimates can be found in the Supplementary Information.

The constant influx of energy due to these two processes heats up the electrons. However, this influx is balanced by the cooling power of the cold crystal lattice. A steady state is established at an effective electron temperature Te, where the cooling power is strong enough to fully balance the drive-induced heating. The mechanism is dominated by acoustic phonons and is well studied both experimentally96,97,98 and theoretically99 for graphene. The cooling power per electron Pcool is given by

$${P}_{{{{{\rm{cool}}}}}}=\frac{\Sigma \left(\bar{\rho }\right)}{\bar{\rho }}\left({T}_{e}^{4}-{T}_{{{{{\rm{ph}}}}}}^{4}\right),$$
(33)

where the constant \(\Sigma \left(\bar{\rho }\right)/\bar{\rho }\) plays the role of a material dependent coupling. For a conservative estimate, we use the values reported for graphene (see e.g. Ref 98). Theory shows that the cooling power in TMDs is even higher100, such that the effective electron temperature in TMDs will be lower. We find \(\Sigma \left(\bar{\rho }\right)\approx 1\frac{{{{{\rm{mW}}}}}}{{{{{{\rm{K}}}}}}^{4}{{{{{\rm{m}}}}}}^{2}}\) for \(\bar{\rho }\approx 1{0}^{11}{{{{{\rm{cm}}}}}}^{-2}-1{0}^{12}{{{{{\rm{cm}}}}}}^{-2}\), Tph = 4.2 K. A detailed estimation of the rates of photon absorption (see Supplementary Information) gives a heating power of Pdrive = 2.7 ⋅ 106 eV/s, for the driving strength required to reach the instability threshold (see Discussion section). Equating Pcool = Pdrive, we find an effective electron temperature of Te ≈ 20 K. This is well below the typical temperatures in plasmonics experiments79. Moreover, due to the nonlinear dependence of the cooling power Pcool on the electron temperature, increasing the driving power by three orders of magnitude would result in an effective electron temperature of only Te ≈ 100 K.

All in all, we find that driving-induced heating is controlled in the setting we propose. Most importantly, we find that the driving-induced heating is too weak to significantly increase the Landau damping of plasmons, which is strongly suppressed by the \(\sqrt{q}\)- shape of the plasmon dispersion, lying—for the frequencies considered here—outside the particle-hole continuum101.

Discussion

Gapped two dimensional Dirac materials are currently an active area of research in material science102,103 and promising candidates for Floquet engineering. Recently, ARPES measurements revealed light-induced gaps in black phosphorus16 and Floquet-Bloch states in graphene104,105 in the off-resonant regime considered here. Many interesting features of MFPD, such as the enhancement of plasmon quality factors, as well as exceptional points and non-dispersive states, appear below the critical driving strengths determined by the instability condition h > 2γ/ω1, making them accessible for lasers with relatively low powers. To estimate the power necessary to induce the non-equilibrium crystalline phase, we assume typical values for the parameters of our system: Eg = 0.3 eV, ℏΩF = 0.35 eV, λ = 15 eVÅ. Assuming an electron density of \(\bar{\rho }=1.18\cdot 1{0}^{11}/{{{{{\rm{cm}}}}}}^{-2}\), such that the chemical potential is close to, but above the resonance, and a plasmon quality factor of \({{{{\mathcal{Q}}}}}={\omega }_{1}/\gamma \approx 1{0}^{2}\), from the instability condition h > 2γ/ω1, we find the necessary critical amplitude of the electric field to be \(\bar{{{{\mathcal{{E}}}}}}\approx 4\cdot 1{0}^{5}\,{{{{\rm{V}}}}}/{{{{\rm{m}}}}}\) with a modulation amplitude \(\delta \bar{{{{\mathcal{{E}}}}}}=0.5\bar{{{{\mathcal{{E}}}}}}\). Thus the laser intensity required to induce the transition to the crystalline state is by a factor of 104 smaller than in current solid state Floquet engineering experiments12,13,14,16 and generally within the reach of continuous wave lasers. The critical driving strength is essentially determined by the plasmon \({{{{\mathcal{Q}}}}}\). While quality factors of \({{{{\mathcal{Q}}}}}\approx 1.5\cdot 1{0}^{2}\) have been observed in graphene79, quality factors of up to 103−104 are believed to be reachable in principle79,80. Such high quality factors would allow to further reduce the necessary laser intensity. On the other hand, as shown in the section “Heating and Landau damping,” the suppression of heating in the off-resonant regime used by MFPD allows, in principle, to increase the driving power by at least two orders of magnitude. Thus, MFPD may be even achievable with low-quality plasmons, if sufficiently strong drives are used.

The phenomena presented here can be implemented in two dimensional Dirac systems, such as black phosphorus or TMDs106. Another candidate for realizing our ideas is graphene, where Floquet-Bloch states have also been observed at different driving energies14,104,105.

In summary, modulated Floquet parametric driving offers a road to realize new non-equilibrium electron phases with broken translation symmetries in time and space and non-trivial Goldstone modes. Additionally, MFPD opens new possibilities to excite and control THz plasmons by optical or infrared signals. Given the interest in efficient THz technology, the realization of plasmonic parametric amplifiers, time reversal mirrors and other effects predicted for time-varying photonic materials81,82,107 will advance current research on plasmons. A direct observation of exceptional points and non-dispersive regions can be achieved by mapping the plasmon dispersion, e.g., with spectroscopic measurements108, while the crystalline plasmon phase can be detected via scanning near-field optical microscopy which can be used to measure the periodic density δρ of the crystalline state109,110. The plasmon lattice could also be observed through light or electron scattering experiments, where it would act similarly to a 2D grating. Finally, we note that similar physics could be implemented using other types of collective modes, e.g., magnons.

Methods

Slowly varying envelope approximation

To find the exceptional points and instabilities of plasmon waves under MFPD (see section “ Instabilities and exceptional points”), we solve Eq. (12) in the vicinity of the resonance \({\omega }_{{{{{\rm{pl}}}}}}\left(q\right)={\omega }_{1}\) with the slowly varying envelope approximation76. The ansatz

$$\delta {\rho }_{q}={a}_{q}\left(t\right)\cos \left({\omega }_{1}t\right)+{b}_{q}\left(t\right)\sin \left({\omega }_{1}t\right),$$
(34)

when used in Eq. (12), leads to the two equations

$$\begin{array}{rcl}-\frac{1}{2}{\omega }_{1}^{2}h{b}_{q}-2{\dot{a}}_{q}{\omega }_{1}-\gamma {a}_{q}{\omega }_{1}+\left({\omega }_{{{{{\rm{pl}}}}}}^{2}\left(q\right)-{\omega }_{1}^{2}\right){b}_{q}&=&0\\ \frac{1}{2}{\omega }_{1}^{2}h{a}_{q}+2{\dot{b}}_{q}{\omega }_{1}+\gamma {b}_{q}{\omega }_{1}+\left({\omega }_{{{{{\rm{pl}}}}}}^{2}\left(q\right)-{\omega }_{1}^{2}\right){a}_{q}&=&0,\end{array}$$
(35)

where we neglected the second derivatives of aq and bq, as they are of higher order in the small h around \({\omega }_{{{{{\rm{pl}}}}}}\left(q\right)={\omega }_{1}\). Assuming \(a=a\left(0\right){e}^{s\left(q\right)t}\), \(b=b\left(0\right){e}^{s\left(q\right)t}\), leads to Eq. (15).

Analysis of nonlinear pattern formation

In this section we derive the results on the plasmon crystallization presented in the section “Crystallization.” We first study the strip geometry where the y-axis is confined to a width l with l < 2π/q*. In this quasi-1D geometry, we have to replace the Fourier transform of the Coulomb potential \(V\left(q\right)\) in Eq. (13) by

$$V\left(q\right)\approx \int_{0}^{l}dy\int_{-\infty }^{\infty }dx\frac{{e}^{i{{{{\bf{q}}}}}\cdot {{{{\bf{x}}}}}}}{\left\vert {{{{\bf{x}}}}}\right\vert }\approx 2l\left| \ln \frac{\left\vert q\right\vert l}{4}\right| .$$
(36)

As pointed out in the section “Crystallization,” for the analysis of pattern formation caused by parametric instabilities, it is sufficient to consider a projection of Eq. (8) on the subset of linearly unstable modes of Eq. (34)85,87. This excludes second-order nonlinearities. These give rise to frequency doubling modes, which lie outside of the considered subspace. The third-order terms, however, contribute to oscillations at the base frequency ω1. Keeping in mind that u ∝ q* for plasmons, we use the linearized continuity equation \(\delta \dot{\rho }=-\bar{\rho }\nabla {{{{\bf{u}}}}}\) to approximate

$${u}_{s,i}\approx -{\partial }_{i}\frac{\delta {\dot{\rho }}_{s}}{{q}^{*2}\bar{\rho }}.$$
(37)

At this point, it is useful to simplify Eq. (11). Rescaling \(\delta {\rho }_{s}={h}^{1/2}\delta {\tilde{\rho }}_{s}\), we find that to order \({{{{\mathcal{O}}}}}\left(h\right)\), the time dependence of m* in front of the nonlinear terms can be neglected for h ≪ 1. With the approximations described above, for the purpose of finding the modulated pattern of the steady state, Eq. (11) is reduced to

$$\begin{array}{rcl}{\partial }_{t}{m}^{*}\left(t\right){\partial }_{t}\delta {\rho }_{s}+\gamma {\bar{m}}^{*}{\partial }_{t}\delta {\rho }_{s}+{\bar{m}}^{*}{\omega }_{1}^{2}\delta {\rho }_{s}&&\\ -\frac{{\bar{m}}^{*}}{{q}^{*4}{\bar{\rho }}^{2}}{\partial }_{i}{\partial }_{j}\delta {\rho }_{s}\left({\partial }_{i}\delta {\dot{\rho }}_{s}\right)\left({\partial }_{j}\delta {\dot{\rho }}_{s}\right)&=&0,\end{array}$$
(38)

where δρs is given by Eq. (21). Derivatives (except those in parenthesis) act on all functions to their right. An evaluation of Eq. (38) in which modes lying outside the subspace of linearly unstable modes are neglected leads to Eq. (22), which is the nonlinear generalization of the slowly varying mode approximation of Eq. (35).

Deriving the Goldstone modes

Here, we derive the dispersions of the Goldstone-like modes in the symmetry-breaking steady state. Starting from Eq. (28), we write

$$\begin{array}{rcl}\delta \rho &=&\frac{1}{2}\sqrt{\frac{\alpha }{\beta }}\left[\sin \left({\omega }_{1}t-{q}^{*}x-\varphi \left(t,x\right)\right)\right.\\ &&\left.+\sin \left({\omega }_{1}t+{q}^{*}x+\varphi \left(t,x\right)\right)\right],\end{array}$$
(39)

and choose the ansatz

$$\varphi \left(t,x\right)={{{{\rm{Re}}}}}{\varphi }_{0}{e}^{-i\Omega t+iQ\cdot x}$$
(40)

for \(\phi \left(t,x\right)\), where

$$\frac{Q}{{q}^{*}}\ll 1,\frac{\Omega }{{\omega }_{1}}\ll 1.$$
(41)

We insert Eq. (39) into Eq. (11) and compare the coefficients in front of the resulting \(\sin \left[{\omega }_{1}t\pm {q}^{*}x\pm \varphi \left(t,x\right)\right]\) and \(\cos \left[{\omega }_{1}t\pm {q}^{*}x\pm \varphi \left(t,x\right)\right]\) terms in the equations. The equation governing the propagation of the local phase shift \(\varphi \left(t,x\right)\) follows from the cosine terms. To leading order in \(\varphi \left(t,x\right)\), Q/qs and Ω/ω1, we find

$$\frac{{\partial }^{2}}{\partial {t}^{2}}\varphi=\frac{{\omega }_{1}^{2}/{q}^{*2}}{1-h/2}\left(1+\frac{5}{2}h\right)\frac{{\partial }^{2}}{\partial {x}^{2}}\varphi .$$
(42)

The wave equation (42) leads to the dispersion of Goldstone-like phonons (29) in the section “Goldstone-like phonons.”. The equation obtained from comparing the coefficients in front of the sine terms is fulfilled identically to the leading order in Ω/ω1. A more detailed version of this derivation can be found in the Supplementary Information.