Dynamical transition in controllable quantum neural networks with large depth

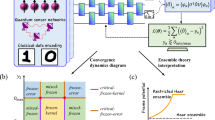
Abstract

Understanding the training dynamics of quantum neural networks is a fundamental task in quantum information science with wide impact in physics, chemistry and machine learning. In this work, we show that the late-time training dynamics of quantum neural networks with a quadratic loss function can be described by the generalized Lotka-Volterra equations, leading to a transcritical bifurcation transition in the dynamics. When the targeted value of loss function crosses the minimum achievable value from above to below, the dynamics evolve from a frozen-kernel dynamics to a frozen-error dynamics, showing a duality between the quantum neural tangent kernel and the total error. In both regions, the convergence towards the fixed point is exponential, while at the critical point becomes polynomial. We provide a non-perturbative analytical theory to explain the transition via a restricted Haar ensemble at late time, when the output state approaches the steady state. Via mapping the Hessian to an effective Hamiltonian, we also identify a linearly vanishing gap at the transition point. Compared with the linear loss function, we show that a quadratic loss function within the frozen-error dynamics enables a speedup in the training convergence. The theory findings are verified experimentally on IBM quantum devices.

Introduction

As a paradigm of near-term quantum computing, variational quantum algorithms^1,2,3,4,5,6 have been widely applied to chemistry^1,7, optimization^2,8, quantum simulation^9,10, condensed matter physics¹¹, communication^12,13, sensing^14,15 and machine learning^{16,17,18,19,20,21,22,23}. Adopting layers of gates and stochastic gradient descent, they are regarded as ‘quantum neural networks’ (QNNs), analog to classical neural networks that are crucial to machine learning. Concepts and methods related to variational quantum algorithms are also beneficial for quantum error correction and quantum control^24,25, bridging near-term applications with the fault-tolerant era.

Despite the progress in applications, theoretical understanding of the training dynamics of QNN is limited, hindering the optimal design of quantum architectures and the theoretical study of quantum advantage in such applications. Previous works adopt tools from quantum information scrambling for empirical study of QNN training^26,27. Recently, the Quantum Neural Tangent Kernel (QNTK) theory presents a potential theoretical framework for an analytical understanding of variational quantum algorithms, at least within certain limits^{28,29,30,31,32}, revealing deep connections to their classical machine learning counterparts^{33,34,35,36,37,38,39,40,41,42,43}. However, the theory of QNTK relies on the assumption of sufficiently random quantum circuit set-ups known as unitary k-designs^44,45,46,47 that is only true at random initialization, preventing the theory from describing the more important late-time training dynamics. Similar limitations also exist for other theoretical works^{4,48,49,50,51}.

In this work, we go beyond QNTK theory and identify a dynamical transition in the training of QNNs with a quadratic loss function, when the target loss function value O₀ cross the minimum achievable value (ground state energy ${O}_{\min }$). We show that the training dynamics of deep QNNs is governed by the generalized Lotka-Volterra (LV) equations describing a competitive duality between the quantum neural tangent kernel and the total error. The LV equations can be analytically solved and the dynamics is determined by the value of a conserved quantity. When the target value crosses ${O}_{\min }$, the conserved quantity changes sign and induces a transcritical bifurcation transition. As depicted in Fig. 1, in the frozen-kernel dynamics where ${O}_{0} > {O}_{\min }$ is in the bulk of spectrum, the kernel is approaching a constant while the error decays exponentially with training steps; At the critical point when ${O}_{0}={O}_{\min }$ exactly, both the kernel and the error decay polynomially; In the frozen-error dynamics when ${O}_{0} < {O}_{\min }$ is unachievable, the output from QNN still converges to the ground state leaving the error approaching a constant ${O}_{\min }-{O}_{0}$, while the kernel experiences an exponential decay. We provide a non-perturbative analytical theory to explain the dynamical transition via a restricted Haar ensemble at late time, when the QNN output state approaches the steady state. We also identify a vanishing Hessian gap at the transition point, which corresponds to Hamiltonian gap closing in the imaginary-time Schrödinger equation interpretation. While our theory analyses assume the large-depth limit, the dynamical transition is also numerically identified in QNNs with limited depths. Compared to the exponential decay of linear loss function with a non-tunable exponent, we identify convergence speed-up via tuning the quadratic loss function to be within the frozen-error dynamics. The theory findings are experimentally verified on IBM quantum devices. Our results imply that designing the loss function properly is important to achieve fast convergence.

Fig. 1: Illustration of setup and main results of this work.

We study the training dynamics of quantum neural networks with loss function ${{{\mathcal{L}}}}({{{\boldsymbol{\theta }}}})={(\langle \hat{O}\rangle -{O}_{0})}^{2}/2$, and identify a dynamical transition. We derive a first-principle generalized Lotka-Volterra model to characterize it, and also provide interpretations from random unitary ensemble and Schrödinger equation.

Results

We begin by first introducing the model of the QNN and the necessary quantities. Then, we uncover the dynamical transition phenomena as a bifurcation transition in LV model. The unitary ensemble theory is then developed to support assumptions in obtaining the LV model. Afterwards, we characterize the transition with tools from statistical physics. After finishing the theory, we provide numerical extensions and discuss the potential training speed-up brought by our results. Finally, we confirm the results in experiments.

Training dynamics of quantum neural networks

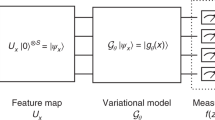
A D-depth QNN is composed of D layers of parameterized quantum circuits, realizing a unitary transform $\hat{U}({{{\boldsymbol{\theta }}}})$ on n qubits, with L variational parameters θ = (θ₁, …, θ_L). The gate configuration of each layer varies between different circuit ansatz (see Methods for examples). When inputting a trivial state ${\left\vert 0\right\rangle }^{\otimes n}$, the final output state of the neural network $\left\vert \psi ({{{\boldsymbol{\theta }}}})\right\rangle=\hat{U}({{{\boldsymbol{\theta }}}}){\left\vert 0\right\rangle }^{\otimes n}$, from which one can measure a Hermitian observable $\hat{O}$ leading to expectation value $\langle \hat{O}\rangle=\langle \psi ({{{\boldsymbol{\theta }}}})| \hat{O}| \psi ({{{\boldsymbol{\theta }}}})\rangle$. To optimize the expectation of an observable $\hat{O}$ towards the target value O₀, a general choice of loss function is in a quadratic form,

$${{{\mathcal{L}}}}({{{\boldsymbol{\theta }}}})=\frac{1}{2}{\left(\langle \hat{O}\rangle -{O}_{0}\right)}^{2}\equiv \frac{1}{2}\epsilon {({{{\boldsymbol{\theta }}}})}^{2},$$

(1)

where the total error $\epsilon ({{{\boldsymbol{\theta }}}})=\langle \hat{O}\rangle -{O}_{0}.$ Suppose observable $\hat{O}$ has possible values in the range of $[{O}_{\min },{O}_{\max }]$. Without further specification, ${O}_{\min }$ and ${O}_{\max }$ refer to the minimum and maximum eigenvalue of $\hat{O}$. Now due to symmetry of maximum and minimum in optimization problems, we assume ${O}_{0} < {O}_{\max }$ is true.

A QNN goes through training to minimize the loss function. In each training step, every variational parameter is updated by the gradient descent

$$\delta {\theta }_{\ell }(t)\equiv {\theta }_{\ell }(t+1)-{\theta }_{\ell }(t)=-\eta \frac{\partial {{{\mathcal{L}}}}({{{\boldsymbol{\theta }}}})}{\partial {\theta }_{\ell }}=-\eta \epsilon ({{{\boldsymbol{\theta }}}})\frac{\partial \epsilon ({{{\boldsymbol{\theta }}}})}{\partial {\theta }_{\ell }},$$

(2)

where η is the fixed learning rate and t is the discrete number of time steps in the training. With the update of parameters θ, quantities depending on θ also acquire new values in each training step. For simplicity of notion, we denote their dependence on t explicitly omitting θ, e.g. ϵ(t) ≡ ϵ(θ(t)). To study the convergence, we separate the error into two parts, ϵ(t) ≡ ε(t) + R consists of a constant remaining term $R={\lim}_{t\to \infty}\epsilon (t)$ and a vanishing residual error ε(t). When η ≪ 1 is small, the total error is updated as

$$\delta \epsilon (t)\simeq {\sum}_{\ell }\frac{\partial \epsilon ({{{\boldsymbol{\theta }}}})}{\partial {\theta }_{\ell }}\delta {\theta }_{\ell }+\frac{1}{2}{\sum}_{{\ell }_{1},{\ell }_{2}}\frac{{\partial }^{2}\epsilon ({{{\boldsymbol{\theta }}}})}{\partial {\theta }_{{\ell }_{1}}\partial {\theta }_{{\ell }_{2}}}\delta {\theta }_{{\ell }_{1}}\delta {\theta }_{{\ell }_{2}}$$

(3)

$$=-\eta \epsilon (t)K(t)+\frac{1}{2}{\eta }^{2}\epsilon {(t)}^{2}\mu (t),$$

(4)

where the QNTK K and dQNTK μ are defined as²⁹

$$K(t)\equiv {\sum}_{\ell }{\left.{\left(\frac{\partial \epsilon ({{{\boldsymbol{\theta }}}})}{\partial {\theta }_{\ell }}\right)}^{2}\right| }_{{{{\boldsymbol{\theta }}}}={{{\boldsymbol{\theta }}}}(t)},$$

(5)

$$\mu (t)\equiv {\sum}_{{\ell }_{1},{\ell }_{2}}{\left.\frac{{\partial }^{2}\epsilon ({{{\boldsymbol{\theta }}}})}{\partial {\theta }_{{\ell }_{1}}\partial {\theta }_{{\ell }_{2}}}\frac{\partial \epsilon ({{{\boldsymbol{\theta }}}})}{\partial {\theta }_{{\ell }_{1}}}\frac{\partial \epsilon ({{{\boldsymbol{\theta }}}})}{\partial {\theta }_{{\ell }_{2}}}\right| }_{{{{\boldsymbol{\theta }}}}={{{\boldsymbol{\theta }}}}(t)}.$$

(6)

In the dynamics of ϵ(t), as η ≪ 1, we focus on the first order of η in Eq. (4) as

$$\delta \epsilon (t)=-\eta \epsilon (t)K(t)+{{{\mathcal{O}}}}({\eta }^{2}).$$

(7)

To characterize the dynamics of ϵ(t), it is necessary and sufficient to understand the dynamics of QNTK K(t). Towards this end, we derive a first-order difference equation for QNTK K(t) as (see details in Supplementary Note 1)

$$\delta K(t)=-2\eta \epsilon (t)\mu (t)+O({\eta }^{2}).$$

(8)

Combining Eq. (7) and Eq. (8), we aim to develop the dynamical model in training QNNs.

Dynamical transition

Our major finding is that when the circuit is deep and controllable, the QNN dynamics exhibit a dynamical transition at ${O}_{\min }$ (and ${O}_{\max }$ similarly) as we depict in Fig. 2, where a QNN with random Pauli ansatz (RPA) is utilized to optimize the XXZ model Hamiltonian (see Methods for details of the circuit and observable).

Fig. 2: Dynamics in QNN in the example of XXZ model.

The top and bottom panels show the dynamics of total error ϵ(t) and QNTK K(t) with respect to the three cases $O_0 \gtreqless O_{\min}$. Blue solid curves represent numerical ensemble average result. Red dashed curves in panels represent theoretical predictions on the dynamics of total error in Eqs. (14)–(16) (from left to right). Grey solid lines show the dynamics for each random sample. The inset in (c1) shows the exponential decay of residual error ε(t). Here random Pauli ansatz (RPA) consists of L = 768 variational parameters (D = L for RPA) on n = 8 qubits, and the parameter in XXZ model is J = 2.

Frozen-kernel dynamics: When ${O}_{0} > {O}_{\min }$, the total error decays exponentially and the energy converges towards O₀, as shown in Fig. 2a1. This is triggered by the frozen QNTK as shown in Fig. 2a2. Each individual random sample (gray) has slightly different value of frozen QNTK due to initialization, while all possess the exponential convergence. Our theory prediction (red dashed) agrees with the actual average (blue solid) for both the ensemble averaged QNTK $\overline{K}$ and the error, while deviations due to early time dynamics can be seen (see Methods for details).

Critical point: When targeting right at the GS energy ${O}_{0}={O}_{\min }$, both the total error and QNTK decay as 1/t, independent of system dimension d. As shown in Fig. 2b2, the QNTK ensemble average (blue solid) agrees very well with the theory prediction shown as the red dashed line. Due to initial time discrepancy in QNTK that is beyond our late time theory, the actual error dynamics has a constant deviation from the theory prediction (red dashed), however still has the 1/t late time scaling, as shown in Fig. 2b1.

Frozen-error dynamics: When targeting below the GS energy ${O}_{0} < {O}_{\min }$, the total error converges to a constant $R={O}_{\min }-{O}_{0} \, > \, 0$ exponentially, as shown in Fig. 2c1. The inset shows the exponential convergence via the residual error ε = ϵ − R. In this case, the QNTK also decays exponentially with the training steps, as shown in Fig. 2c2. Deviation between the theory (red dashed) and numerical results (blue solid) can be seen due to early time dynamics beyond our theory.

Generalized Lotka-Volterra model: bifurcation

In this section, we reveal the nature of the transition as a transcritical bifurcation of an effective nonlinear dynamical equation. With large depth D ≫ 1 and full control, QNNs are commonly modeled as a random unitary^4,29,51. However, at late time, the convergence of QNN training imposes constraints on the QNN unitary. As we will detail in ‘Unitary ensemble theory’ section, assuming that the late-time QNN is typical among random ensemble of unitaries under the convergence constraint, we can show that the relative dQNTK—the ratio of dQNTK and QNTK

$$\lambda (t)=\mu (t)/K(t)$$

(9)

converges towards a constant dependent on the number of parameters L and Hilbert space dimension of the system d = 2ⁿ. Under the assumption that λ(t) = λ being a constant and taking the continuous limit, Eqs. (7) and (8) lead to a coupled set of equations,

$$\left\{\begin{array}{l}{\partial }_{t}\epsilon (t)\quad=-\eta \epsilon (t)K(t) \hfill \\ {\partial }_{t}K(t)\quad \!=-2\eta \lambda \epsilon (t)K(t)\end{array}\right.$$

(10)

to the leading order in η. This is the generalized Lotka-Volterra equation developed in modeling nonlinear population dynamics of species competing for some common resource⁵². The two ‘species’ represented by K and ϵ are in direct competition as the interaction terms are negative. As Eqs. (10) have zero intrinsic birth/death rate, there is no stable attractor where all species K(t) and ϵ(t) are positive, as sketched in Fig. 1 bottom left, where 2λϵ and K are the x and y axis. From Eqs. (10), we can identify the conserved quantity at late time

$$C=K(t)-2\lambda \epsilon (t)={{{\rm{const}}}}.$$

(11)

Each trajectory of (2λϵ(t), K(t)) governed by Eqs. (10) is thus a straight line quantified by the conserved quantity C. We verify the trajectory from the conserved quantity of Eq. (11) in Fig. 3(b), where good agreement between QNN dynamics (solid) and generalized LV dynamics (dashed) can be identified. The conservation law in Eq. (11) indicates that a classical Hamiltonian description of LV dynamics is possible, via mapping the scaled error and kernel to the canonical position and momentum (see Methods). Therefore, the position-momentum duality in Hamiltonian formulation implies an error-kernel duality between K and ϵ.

Fig. 3: Classical dynamics interpretation of total error and QNTK dynamics.

a The RHS of Eq. (12) shows a bifurcation. The gray region is nonphysical as K≥0. In the physical region (K≥0), we have a single stable fixed point K = C when C > 0, corresponding to the frozen-kernel dynamics (blue in b); and a single stable fixed point K = 0 when C≤0, corresponding to the frozen error dynamics and critical point (green and red in b) separately. b Trajectories of (2λ(∞)ϵ(t), K(t)) in dynamics of QNN with different $O_0 \gtreqless O_{\min}$, plotted in solid blue, red and green. Dashed curves show the trajectory from Eq. (11). The logarithmic scale is taken to focus on the late-time comparison. c The dynamics of corresponding λ(t) = μ(t)/K(t). The inset shows the dynamics of ζ(t) = ϵ(t)μ(t)/K(t)². The observable is XXZ model with J = 2, and QNN is a n = 6-qubit RPA with L = 192 parameters (for RPA D = L). The legend in b is also shared with (c) and its inset.

Thanks to the conserved quantity C, we can reduce the coupled differential equations of the LV model in Eq. (10) to a single variable differential equation with the kernel or the error alone, e.g.,

$${\partial }_{t}K(t)=\eta (C-K(t))K(t).$$

(12)

This is a canonical example of a transcritical bifurcation, with two fixed points K = C and K = 0⁵³. To see this, we plot the RHS of Eq. (12) in Fig. 3a. When C > 0 (blue curve), via the sign of ∂_tK, we can see that only K = C (therefore ϵ = 0) is stable, corresponding to the frozen-kernel dynamics. On the other hand, when C < 0 (green curve), K = 0 (therefore 2λϵ = − C > 0) is the only stable fixed point, corresponding to the frozen-error dynamics. Specifically, for C = 0 (red curve), the two candidates collide and K = 0 (therefore ϵ = 0) becomes the bifurcation point. As the fixed points collide and their stability exchange through the bifurcation point (K, C) = (0, 0), the transition is identified as the transcritical bifurcation.

Overall, we see that the two dynamics (and the critical point) of the QNN dynamics has a one-to-one correspondence to the two families of fixed points (and their common fixed point) of the generalized LV equation. The conserved quantity C = K(t) − 2λϵ(t) = (K(t)² − 2ϵ(t)μ(t))/K(t). Since K(t) > 0 at any finite time, the sign of constant is determined by the dynamical index defined as

$$\zeta=\epsilon (t)\mu (t)/K{(t)}^{2}.$$

(13)

If ζ ⋚ 1/2, we have C ⋛ 0, determining the bifurcation dynamics.

Indeed, the analytical closed-form solution (see Methods) to the LV dynamics of Eqs. (10) supports the following theorem at the t ≫ 1 late time limit.

Theorem 1

Assuming relative dQNTK λ = μ(t)/K(t) being a constant at late time, the QNN dynamics is governed by the generalized Lotka-Volterra equation in Eq. (10) and possesses a bifurcation to two different branches of dynamics, depending on the value of a conserved quantity C = K(t) − 2λϵ(t) = (1 − 2ζ)K(t) or equivalently the dynamical index ζ = ϵ(t)μ(t)/K(t)².

• 1. When ζ < 1/2 thus C > 0, we have the ‘frozen-kernel dynamics’ (c.f.²⁹), where the QNTK K(t) = C is frozen and

  $$\epsilon (t)\propto {e}^{-\eta Ct}.$$

  (14)

• 2. When ζ = 1/2 thus C = 0, we have the ‘critical point’, where both the QNTK and total error decay polynomially,

  $$K(t)=2\lambda \epsilon (t)=1/(\eta t+c),$$

  (15)

  with c being a constant.

• 3. When ζ > 1/2 thus C < 0, we have the ‘frozen-error dynamics’, where the total error ϵ(t) = R is frozen and both the kernel and the residual error decay exponentially

  $$K(t)=2\lambda \varepsilon (t)\propto {e}^{-2\eta \lambda Rt}.$$

  (16)

The bifurcation can be connected to $O_0 \gtreqless O_{\min}$ intuitively. When ${O}_{0} < {O}_{\min }$, it is clear that R > 0 and we expect dynamical index ζ > 1/2 and C < 0 so that it is the ‘frozen-error dynamics’. When ${O}_{0} > {O}_{\min }$, we know the total error will decay to zero eventually, and therefore we can correspond this branch to the ‘frozen-kernel dynamics’, where dynamical index ζ < 1/2 and C > 0. The case ${O}_{0}={O}_{\min }$ is therefore the critical point. In Fig. 3(c) inset, we indeed see the dynamical index ζ → 0, 1/2, + ∞ when $O_0 \gtreqless O_{\min}$. In our later theory analyses, we will make this connection rigorous between $O_0 \gtreqless O_{\min}$, the dynamical index ζ ⋚ 1/2 and the bifurcation transition.

Unitary ensemble theory

In this section, we provide analytical results to resolve two missing pieces of the LV model—the assumption that the relative dQNTK λ in Eq. (9) is a constant at late time and the connection between the dynamical index ζ ⋚ 1/2 in Eq. (13) and the $O_0 \gtreqless O_{\min}$ cases. Our analyses will rely on large depth D ≫ 1 (equivalently L ≫ 1), which allows us to model each realization of the QNN $\hat{U}({{{\boldsymbol{\theta }}}})$ as a sample from an ensemble of unitaries and consider ensemble averaged values to represent the typical case, $\overline{\zeta }=\overline{\epsilon \mu }/{\overline{K}}^{2},\overline{\lambda }=\overline{\mu }/\overline{K}$. Note that we take the ratio between averaged quantity via considering the sign of $\overline{C}$. The ordering of ensemble averages has negligible effects (see Supplementary Note 12).

As the QNN is initialized randomly at the beginning, the unitary $\hat{U}({{{\boldsymbol{\theta }}}})$ being implemented can be regarded as typical ones satisfying Haar random distribution^4,29,51, regardless of the circuit ansatz. While this is a good approximation at initial time, we notice that at late time, the QNN $\hat{U}({{{\boldsymbol{\theta }}}})$ is constrained in the sense that it maps the initial trivial state (e.g. product of $\left\vert 0\right\rangle$) towards a single quantum state, regardless of whether the quantum state is the unique optimum or not. Therefore, the late-time dynamics are always restricted due to convergence, which we model as the restricted Haar ensemble with a block-diagonal form,

$${{{{\mathcal{E}}}}}_{{{{\rm{RH}}}}}=\left\{U| U=\left(\begin{array}{cc}1&{{{\boldsymbol{0}}}}\\ {{{\boldsymbol{0}}}}&V\end{array}\right)\right\},$$

(17)

where V is a unitary with dimension d − 1 following a sub-system Haar random distribution (only 4-design is necessary). Here we have set the basis of the first column and row to represent mapping from the initial state to the final converged state. At late time, QNN converges to a restricted Haar ensemble determined by the converged state. When the converged state is unique, frame potential⁴⁴ of the ensemble can be evaluated by considering different training trajectories, which confirms the ansatz in Eq. (17), as shown in Fig. 1 and Supplementary Note 7.

The ensemble average for a general traceless operator is challenging to analytically obtain. To gain insights to QNN training, we consider a much simpler problem of state preparation, where $\hat{O}=\left\vert \Phi \right\rangle \left\langle \Phi \right\vert$ is a projector. In this case, we are interested in target values O₀ near the maximum loss function ${O}_{\max }=1$. Under such restricted Haar ensemble, we have the following lemma.

Lemma 2

When the circuit satisfies the restricted Haar random (restricted 4-design) ensemble and D ≫ 1 (therefore L ≫ 1), in state preparation tasks the relative dQNTK $\overline{{\lambda }_{\infty }}$ goes to an L, d dependent constant. When ${O}_{0} < {O}_{\max }$, the dynamical index $\overline{{\zeta }_{\infty }}=0$; when ${O}_{0}={O}_{\max }$, the dynamical index $\overline{{\zeta }_{\infty }}=1/2;$ when ${O}_{0} > {O}_{\max }$, the dynamical index ζ diverges to  + ∞.

This lemma derives from Theorem 3 in the Method.

While our results are general, in our numerical study that verifies the analytical results, we adopt the random Pauli ansatz (RPA)²⁹ as an example (see Methods). Due to symmetry between maximum and minimum in optimization, this restricted Haar ensemble therefore fully explains the branches of dynamics in Theorem 1 quantitatively and the assumption that λ approaches a constant qualitatively. From asymptotic analyses of the restricted Haar ensemble in Supplementary Note 12, we also have both λ, C ∝ L/d, thus the exponential decay in LV has exponent ∝ ηLt/d. Indeed, in a computation, ηLt describes the resource—when a number of parameters L is larger, one needs to compute and update more parameters, while taking fewer steps t to converge.

As we show in Methods, Haar ensemble fails to capture the ζ dynamics nor the bifurcation transition. Only in the case of frozen-kernel dynamics, as the kernel does not change much during the dynamics, the Haar predictions roughly agree with the actual kernel, as shown in Fig. 2a2 (see Methods).

Schrödinger equation interpretation

Besides the LV dynamics, we can also connect the transition to the gap closing of the Hessian, via interpreting the training dynamics around the extremum as imaginary Schrodinger evolution as we detail below. The gradient descent dynamics in Eq. (2) leads to the time evolution of the quantum state $\left\vert \psi ({{{\boldsymbol{\theta }}}})\right\rangle$, where θ are the variational parameters. In the late time limit, omitting the t dependence in our notation, we can expand the shifts δθ_ℓ around the extremum θ^* to second order as

$$\delta {{{\boldsymbol{\theta }}}}\simeq -\eta M({{{\boldsymbol{\theta }}}}){| }_{{{{\boldsymbol{\theta }}}}={{{{\boldsymbol{\theta }}}}}^{*}}\left({{{\boldsymbol{\theta }}}}-{{{{\boldsymbol{\theta }}}}}^{*}\right),$$

(18)

where the first-order term vanishes due to convergence and the Hessian matrix M(θ) is

$${M}_{{\ell }_{1}{\ell }_{2}}({{{\boldsymbol{\theta }}}})=\left(\frac{{\partial }^{2}{{{\mathcal{L}}}}({{{\boldsymbol{\theta }}}})}{\partial {\theta }_{{\ell }_{1}}\partial {\theta }_{{\ell }_{2}}}\right)=\frac{\partial \epsilon ({{{\boldsymbol{\theta }}}})}{\partial {\theta }_{{\ell }_{1}}}\frac{\partial \epsilon ({{{\boldsymbol{\theta }}}})}{\partial {\theta }_{{\ell }_{2}}}+\epsilon ({{{\boldsymbol{\theta }}}})\frac{{\partial }^{2}\epsilon ({{{\boldsymbol{\theta }}}})}{\partial {\theta }_{{\ell }_{1}}\partial {\theta }_{{\ell }_{2}}}.$$

(19)

We can then model a difference equation for the unnormalized “differential state” $\left\vert \Psi ({{{\boldsymbol{\theta }}}})\right\rangle \equiv \left\vert \psi ({{{\boldsymbol{\theta }}}})\right\rangle -\left\vert \psi ({{{{\boldsymbol{\theta }}}}}^{*})\right\rangle$ as

$$\delta \left\vert \Psi ({{{\boldsymbol{\theta }}}})\right\rangle=-\eta {H}_{\infty }({{{\boldsymbol{\theta }}}})\left\vert \Psi ({{{\boldsymbol{\theta }}}})\right\rangle,$$

(20)

where H_∞(θ) ∼ M(θ) is similar to the Hessian matrix (see Supplementary Note 2). The difference equation can be interpreted as an imaginary time Schrödinger equation, and we identify a transition with gap closing of H_∞ (equivalently M(θ)) driven by O₀ at the infinite time limit.

To provide insight into the transition, we explore the behaviors of the gap of Hessian matrix. We consider the Hessian eigenvalues at the late time limit of t → ∞ and large circuit depth in Fig. 4. For frozen-kernel dynamics of ${O}_{\min } < {O}_{0} < {O}_{\max }$, Hessian matrix in Eq. (19) becomes a rank-one matrix with only one nonzero eigenvalue as ϵ(θ) → 0 (see blue in the inset), which equals the kernel and is verified by the orange and black curve in Fig. 4. While for frozen-error dynamics with ${O}_{0} < {O}_{\min }$ (or ${O}_{0} < {O}_{\max }$), due to non-vanishing ϵ(θ), the Hessian has multiple nonzero eigenvalues (see green in the inset). Overall, gap closing is observed at the critical point. Such a transition at a finite system size resembles that for non-Hermitian dynamical systems^54,55,56. More discussions on the statistical physics interpretation and the closing of the gap under different number of parameters can be found in Supplementary Note 2.

Fig. 4: Spectrum gap of the effective Hamiltonian in Schrödinger interpretation of QNN in the example of XXZ model.

The spectrum gap of Hessian matrix of the effective Shrödinger dynamics in t → ∞ (black). The gapless transition point corresponds to ${O}_{0}={O}_{\min },{O}_{\max }$ (red triangles). The orange line represents the QNTK ${\lim }_{t\to \infty }\overline{K}$. Inset shows the Hessian spectrum of the largest 10 eigenvalues for the three cases ${O}_{0} \gtreqless {O}_{\min }$ marked by triangles. The RPA consists of D = 64 layers (equivalently L = 64 parameters) on n = 2 qubits. The parameters in XXZ model is J = 2.

Dynamics of limited-depth QNN

We have so far focused on controllable QNNs with a universal gate set and large depth. In particular, for a general observable $\hat{O}$, reaching ${O}_{\min }$ may require a circuit of exponential depth (in the number of qubits)⁵⁷. In addition, Lemma 2 requires the (restricted) 4-design that involves a polynomial circuit depth. However, we point out that these depth requirements may be only necessary for the theory derivations and not necessary for the transition phenomenon. Indeed, it is an interesting question whether the transition still exists when the circuit is not controllable—either the ansatz is not universal^58,59 or the depth is limited. Here we provide some results to the limited depth region of the QNNs under study. In this case, the circuit depth L is limited such that the QNN’s minimum achievable value of the observable ${O}_{\min }(L)$ deviates from the ground state energy ${O}_{\min }$. Such a scenario is often referred to as underparameterization.

We first consider the relative dQNTK $\overline{{\lambda }_{\infty }}$ and dynamical index $\overline{{\zeta }_{\infty }}$ versus the depth. In Lemma 2, we provide a justification of both quantities being constants for QNNs with a large depth D to approach the restricted 4-design. In Fig. 5, we present a numerical example for the target O₀ = 1 in state-preparation tasks. The relative sample fluctuations, defined as the standard deviation compared to its mean, decay in a power-law scaling with L, and thus vanish in the asymptotic limit of L ≫ 1. The mean values $\overline{{\lambda }_{\infty }}\propto -L$ and $\overline{{\zeta }_{\infty }}\to 1/2$ are shown in Methods. The decay of fluctuation suggests that the ensemble-average results in Lemma 2 can represent the typical samples. Note that changing the order of the ensemble average for λ_∞ (see Eq. (9)) and ζ_∞ (see Eq. (13)) has negligible effects (see Supplementary Note 12). Similar results for other observables, e.g. XXZ model, are shown in Supplementary Note 12. The speed of convergence roughly agrees with the 4-design requirement of Lemma 2. However, we emphasize that sample fluctuation being small is only a sufficient but not necessary condition for the dynamical transition, as we show in the below example.

Fig. 5: Late-time sample fluctuations.

The standard deviations normalized by mean for the relative dQNTK λ_∞ (a) and dynamical index ζ_∞ (b) are plotted versus the number of parameters L. Red dashed lines represent power-law fitting results. Here the RPA is applied on n = 5 qubits with different L parameters (via tuning number of layers D). The observable is a state projector and the target value is O₀ = 1.

To our surprise, in Fig. 6, we find that the dynamical transition induced by the target value O₀ persists for a QNN with depth D = L = n equaling the number of qubits, much less than what the theory requires. The results align with the dynamics of the controllable QNN presented in Fig. 2. We numerically find that the critical values for limited-depth QNNs, denoted as ${O}_{\min }(L)$, can deviate from the true ground state energy ${O}_{\min }$ of a given observable $\hat{O}$. The critical value for a QNN with L ≪ d will not only depend on depth due to limited expressivity, but also fluctuates due to different initializations. We suspect this may be caused by the training converging to different local minimum traps^49,60. The deviation of the critical point ${O}_{\min }(L)$ from ${O}_{\min }$ indicates that the exponential depth for the convergence to ${O}_{\min }$ is not necessary for the dynamical transition to persist. Moreover, despite the example being also not within the applicability of Lemma 2, the relative dQNTK λ still converges to a constant at late time as we show in SI. However, large sample fluctuation persists in this example due to D = L = n being shallow, violating the unitary design assumption in Lemma 2. However, we point out that as long as λ has small time fluctuation at late time, its dynamics still follows the generalized LV equation discussed in Eq. (10). The above results indicate that the depth requirement of the transition may be much less than that for overparametrization⁶¹.

Fig. 6: Dynamics in limited-depth QNNs in the example of the XXZ model.

All notations share the same meaning as in Fig. 2. The critical point ${O}_{\min }(L)$ for such QNNs depends on L and has sample fluctuations. Here random Pauli ansatz (RPA) consists of L = 6 variational parameters (D = L for RPA) on n = 6 qubits, and the parameter in XXZ model is J = 2.

Speeding up the convergence

While the transition in training dynamics is interesting, the crucial question in practical applications is about how to speed up the training convergence of QNNs. Typically, two types of loss functions are adopted in optimization problems, the quadratic loss function in Eq. (1) that we have focused on, and the linear loss function

$${{{\mathcal{L}}}}({{{\boldsymbol{\theta }}}})=\langle \hat{O}\rangle .$$

(21)

While the linear loss function is widely used in variational quantum eigensolver^7,58, we note that unlike the versatile quadratic loss function that has a tunable target value, a linear function does not allow preparing excited states above the ground state energy nor can it be utilized to data classification and regression. Moreover, for the case of solving the ground state, we show that adopting the quadratic loss function and choosing a target value well below the achievable minimum can speed up the convergence compared to the linear loss function case. Interestingly, ‘shooting for the star’ will allow a faster convergence.

To begin with, we extend our theory framework to characterize the training dynamics of deep controllable QNNs with a linear loss function. To study its convergence, we further consider its residual error $\varepsilon ({{{\boldsymbol{\theta }}}})=\langle \hat{O}\rangle -{O}_{\min }$. Via a similar approach (see details in Supplementary Note 8), we have the dynamical equations for the error ε(t) as

$$\delta \varepsilon (t)=-\eta K(t)+{{{\mathcal{O}}}}({\eta }^{2}),$$

(22)

where K(t) is still the QNTK defined in Eq. (5). The dynamical equation for QNTK K(t) becomes

$$\delta K(t)=-2\eta \mu (t)+{{{\mathcal{O}}}}({\eta }^{2}),$$

(23)

with μ(t) being dQNTK defined in Eq. (6). One may notice that the only difference compared to Eqs. (7) and (8) is the missing of ϵ(t) = ε(t) on RHS due to a linear loss.

In the late-time limit, the results in ‘Unitary ensemble theory’ section still applies to linear loss, and the relative dQNTK λ(t) ≡ μ(t)/K(t) = λ converges to a constant, leading to

$$\left\{\begin{array}{l}{\partial }_{t}\varepsilon (t)\quad=-\eta K(t),\hfill \\ {\partial }_{t}K(t)\quad \!=-2\eta \lambda K(t).\end{array}\right.$$

(24)

Unlike the generalized LV model in Eqs. (10) for the quadratic loss case, here the dynamics of K(t) is self-determined, whereas the dynamics of ε(t) = ϵ(t) is fully determined by K(t)—the kernel-error duality is broken. Eqs. (24) can be directly solved as

$$2\lambda \epsilon (t)=2\lambda \varepsilon (t)=K(t)\propto {e}^{-2\eta \lambda t}.$$

(25)

Both ϵ(t) and K(t) decay exponentially at a fixed rate ∝ λ. In Fig. 7, we present the numerical simulation results (black solid), and observe a good agreement with the theory (black dashed) from Eq. (25).

Fig. 7: Dynamics in QNN in the example of XXZ model with different loss functions.

In a and b, we show the dynamics of residual error ε(t) (equals to total error ϵ(t)) and QNTK K(t) optimized with linear loss function (black solid) and quadratic loss functions with different O₀. O₀ = − 22 (green) corresponds to ${O}_{0}={O}_{\min }$ at critical point and O₀ = −26, −30 (red and blue) correspond to ${O}_{0} < {O}_{\min }$ in frozen error dynamics. Black dashed line indicates the exponential decay rate of the theoretical result in Eq. (25). Thin lines with light colors represent dynamics with different initializations in each case, while the thick lines represent the ensemble average. Here random Pauli ansatz (RPA) consists of L = 192 variational parameters (D = L layers) on n = 6 qubits, and the parameter of XXZ model is J = 2.

With the linear-loss theory developed, we can now compare the convergence speed between the different choices of loss functions in solving the minimum value ${O}_{\min }$ and the corresponding ground state. As indicated in Eq. (25), the linear loss function provides an exponential convergence with the exponent 2ηλ being a constant (black). For quadratic loss functions, at the critical point setting ${O}_{0}={O}_{\min }$, the convergence is polynomial and exponent is zero (green lines in Fig. 7), corresponding to a much slower convergence. However, recall that with a quadratic loss function, one can set ${O}_{0} < {O}_{\min }$ corresponding to the frozen error dynamics, where the residual error ε(t) decays exponentially with the exponent 2ηλR (see Eq. (16)). Here the residual R is freely tunable by the target value O₀. Therefore, an appropriate choice of O₀ can provide a larger exponent and therefore faster convergence towards the solution, and we verify it in Fig. 7 through different values of O₀ (red and blue curves). Indeed, setting the target to be unachievable will still converge the output to the ground state, although the remaining error is frozen.

Experimental results

In this section, we consider the experimental-friendly hardware-efficient ansatz (HEA) to experimentally verify our results on real IBM quantum devices. Each layer of HEA consists of single qubit rotations along Y and Z directions, and followed by CNOT gates on nearest neighbors in a brickwall style⁷. Our experiments adopt the hardware IBM Kolkata, an IBM Falcon r5.11 hardware with 27 qubits, via IBM Qiskit⁶². The device has median T₁ ∼ 98.97 us, median T₂ ∼ 58.21us, median CNOT error ∼ 9.546 × 10⁻³, median SX error ∼ 2.374 × 10⁻⁴, and median readout error ∼ 1.110 × 10⁻². We randomly assign the initial variational angles, distributing them within the range of [0, 2π), and maintain consistency across all experiments. To suppress the impact of error, we average the results over 12 independent experiments conducted under the same setup for three distinct choices, O₀ = −10, −12, −14. In Fig. 8, the experimental data (solid) on IBM Kolkata agree well with the noisy theory model (dashed) and indicate the frozen-error dynamics with constant error (green), the critical point of polynomial decaying error (red) and the frozen-kernel dynamics of exponential decaying error (blue). Individual training data and noisy theory model are presented in Supplementary Note 10.

Fig. 8: Dynamics of total error ϵ(t) on IBM quantum devices, Kolkata.

Solid and dashed curves represent experimental and theoretical results. An n = 2 qubit D = 4-layer hardware efficient ansatz (with L = 16 parameters) is utilized to optimize with respect to XXZ model observable with J = 4. The shaded areas represent the fluctuation (standard deviation) in the experimental data.

Discussion

Our results go beyond the early-time Haar random ensemble widely adopted in QNN study^4,29,51 and reveal rich physics in the dynamical transition controlled by the target loss function. The target-driven transcritical bifurcation transition in the dynamics of QNN suggests a different source to the transition without symmetry breaking. From the Schrödinger equation interpretation, there may exist other unexplored sources that can induce dynamical transition, especially when the QNN has limited depth and controllability. In practical applications, the dynamical transition guides us towards better design of loss functions to speed up the training convergence.

Another intriguing question pertains to the differences between classical and quantum machine learning within this formalism. In our examples, the target O₀ can be interpreted as a single piece of supervised data in a supervised machine learning task. Therefore, the dynamical transition we have discovered could be seen as a simplified version of a theory of data. Classical machine learning also extensively explores dynamical transitions, whether in relation to learning rate dynamics^63,64 or the depth of classical neural networks^43,65. It is an open question whether some results similar to ours can be established for classical machine learning, especially in the context of the large-width regime of classical neural networks⁶⁶. It is also an open problem how our results can generalize to the multiple data case.

Finally, we clarify the difference of our results to some related works. Firstly, while existing works^{28,29,30,31,33} on the quantum neural tangent kernel provide a perturbative explanation of gradient descent dynamics that fails to uncover the dynamical transition, our work uncovers the dynamical transition and formulates non-perturbative critical theories about the transition triggered by modifications in the quantum data. Secondly, we have developed a non-perturbative, phenomenological model using the generalized Lotka-Volterra equations to describe the dynamics as a transcritical bifurcation transition, providing a first-principle explanation using the restricted Haar ensemble. Thirdly, we provide an interpretation of the gradient descent dynamics using Schrödinger’s equation in imaginary time, where the Hessian spectra can be mapped to the effective Hamiltonian using the language of physics, allowing us to study the effective spectral gap. Finally, using correlated dynamics of the Haar ensemble, we offer a more precise derivation of the statistics of the quantum neural tangent kernel, going beyond ref. ²⁹.

Methods

QNN ansatz and details of the tasks

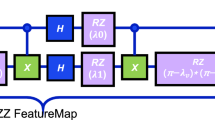
The random Pauli ansatz (RPA) circuit is constructed as

$$\hat{U}({{{\boldsymbol{\theta }}}})={\prod}_{\ell=1}^{D}{\hat{W}}_{\ell }{\hat{V}}_{\ell }({\theta }_{\ell }),$$

(26)

where θ = (θ₁, …, θ_L) are the variational parameters. For RPA, D = L. Here ${\{{\hat{W}}_{\ell }\}}_{\ell=1}^{L}\in {{{{\mathcal{U}}}}}_{{{{\rm{Haar}}}}}(d)$ is a set of fixed Haar random unitaries with dimension d = 2ⁿ, and ${\hat{V}}_{\ell }$ is a n-qubit rotation gate defined to be

$${\hat{V}}_{\ell }({\theta }_{\ell })={e}^{-i{\theta }_{\ell }{\hat{X}}_{\ell }/2},$$

(27)

where ${\hat{X}}_{\ell }\in {\{{\hat{\sigma }}^{x},{\hat{\sigma }}^{y},{\hat{\sigma }}^{z}\}}^{\otimes n}$ is a random n-qubit Pauli operator nontrivially supported on every qubit. Once a circuit is constructed, ${\{{\hat{X}}_{\ell },{\hat{W}}_{\ell }\}}_{\ell=1}^{L}$ are fixed through the optimization. Note that our results also hold for other typical universal ansatz of QNN, for instance, hardware efficient ansatz (see ‘Experimental results’ and Supplementary Note 10).

In the main text, some of our main results are derived for general observable $\hat{O}$. To simplify our expressions, we often consider $\hat{O}$ to be tracelss, for instance a spin Hamiltonian, which is not essential to our conclusions. A general traceless operator can be expressed as random mixture of Pauli strings (excluding identity)

$$\hat{O}={\sum}_{i=1}^{N}{c}_{i}{\hat{P}}_{i}$$

(28)

with real coefficients ${c}_{i}\in {\mathbb{R}}$ and nontrivial Pauli ${\hat{P}}_{i}\in {\{\hat{{\mathbb{I}}},{\hat{\sigma }}^{x},{\hat{\sigma }}^{y},{\hat{\sigma }}^{z}\}}^{\otimes n}/\{{\hat{{\mathbb{I}}}}^{\otimes n}\}$. To obtain explicit expressions, we also consider the XXZ model, described by

$${\hat{O}}_{{{{\rm{XXZ}}}}}=-{\sum}_{i=1}^{n}\left[{\hat{\sigma }}_{i}^{x}{\hat{\sigma }}_{i+1}^{x}+{\hat{\sigma }}_{i}^{y}{\hat{\sigma }}_{i+1}^{y}+J\left({\hat{\sigma }}_{i}^{z}{\hat{\sigma }}_{i+1}^{z}+{\hat{\sigma }}_{i}^{z}\right)\right].$$

(29)

To help understanding the non-frozen QNTK phenomena, we also consider a state preparation case with the observable $\hat{O}=\left\vert \Phi \right\rangle \left\langle \Phi \right\vert$, where $\left\vert \Phi \right\rangle$ is the target state.

Hamiltonian description and analytical solution of the LV dynamics

From the conservation law in Eq. (11), we can introduce the canonical coordinates

$$P=\log (K),\ Q=\log (2\lambda \epsilon )$$

(30)

and the associated Hamiltonian

$$H(Q,P)=\eta ({e}^{Q}-{e}^{P})\equiv \eta (2\lambda \epsilon -K),$$

(31)

from which the LV equations in Eq. (10) can be equivalently rewritten as the standard Hamiltonian equation generalizing ref. ⁶⁷,

$$\left\{\begin{array}{l}\frac{{{{\rm{d}}}}Q}{{{{\rm{d}}}}t}\quad=\frac{\partial H}{\partial P}=\{Q,H\},\hfill \\ \frac{{{{\rm{d}}}}P}{{{{\rm{d}}}}t}\quad=-\frac{\partial H}{\partial Q}=\{P,H\},\end{array}\right.$$

(32)

where $\{A,B\}=\frac{\partial A}{\partial Q}\frac{\partial B}{\partial P}-\frac{\partial A}{\partial P}\frac{\partial B}{\partial Q}$ denotes the Poisson bracket. From the position-momentum duality in Hamiltonian formulation, we identify an error-kernel duality between e^Q ∼ ϵ and its gradient e^P = ∣∂ϵ/∂θ∣².

We can obtain an analytical solution of Eq. (10) directly. When C ≠ 0, we have

$$\left\{\begin{array}{l}\lambda \epsilon (t)\quad=C/\left[-2+{B}_{1}{e}^{\eta Ct}\right],\hfill \\ K(t)\quad \, \,=C/\left[1-2{B}_{1}^{-1}{e}^{-\eta Ct}\right],\end{array}\right.$$

(33)

where B₁ is a constant fitting parameter as at an early time we do not expect Eq. (10) to hold. When C = 0, Eq. (10) leads to polynomial decay of both quantities

$$K(t)=2\lambda \epsilon (t)=2/\left(2\eta t+{B}_{2}^{-1}\right),$$

(34)

where B₂ is again a fitting parameter as at an early time we do not expect Eq. (10) to hold. Indeed, we observe the bifurcation, and the convergence towards the fixed points is exponential for C ≶ 0 and polynomial for C = 0.

Details of restricted Haar ensemble

Here we evaluate the average QNTK, relative dQNTK, and dynamical index for the restricted Haar ensemble proposed in Eq. (17). We focus on the state preparation task to enable analytical calculation. As we aim to capture the late time dynamics with the state preparation task, we will be interested in the dynamics when the output state $\left\vert {\psi }_{0}\right\rangle$ has fidelity $\langle \hat{O}\rangle=| \langle {\psi }_{0}| \Phi \rangle {| }^{2}={O}_{0}-R-\kappa$, with κ ∼ o(1) indicating late-time where the observable is already close to its reachable target. Here the constant remaining term R = O₀ − 1 when O₀ > 1 and zero otherwise. Note that identity is the maximum reachable target value in state preparation. Under this ensemble, we have the following result (see details in Supplementary Note 12)

Theorem 3

For state projector observable $\hat{O}=\left\vert \Phi \right\rangle \left\langle \Phi \right\vert$, when the circuit satisfies restricted Haar ensemble, the ensemble average of QNTK, relative dQNTK, and dynamical index

$$\overline{{K}_{\infty }}=\frac{L}{2d}\left({O}_{0}+R\right)\left(1-{O}_{0}-R\right),$$

(35)

$$\overline{{\zeta }_{\infty }}=\frac{R}{{O}_{0}+R-1}\left(1-\frac{1}{2({O}_{0}+R)}+\frac{d}{L}\right),$$

(36)

$$\overline{{\lambda }_{\infty }}=\frac{L}{4d}\left(1-2{O}_{0}-2R\right)-\frac{{O}_{0}+R}{2},$$

(37)

at the L ≫ 1, d ≫ 1 limit, where the target loss function value O₀≥0, remaining constant $R=\min \{1-{O}_{0},0\}$.

Our results are verified numerically in Fig. 9 in state preparation task, where we plot the above asymptotic equations as magenta dashed lines and the full formula in SI as solid red lines. Note that Lemma 2 does not require d ≫ 1, but merely D ≫ 1. Indeed, full expressions in Theorem 3 can also be derived for any finite d, just much more lengthy.

Fig. 9: Ensemble average results under restricted Haar ensemble (top) and Haar ensemble (bottom).

In top panel, we plot a $\overline{{K}_{\infty }}$ versus O₀ with L = 512 fixed, b $\overline{{\zeta }_{\infty }}$ versus L, $\overline{{\lambda }_{\infty }}$ versus (c) L and d n with L = 512 at late time in state preparation. We set O₀ = 1 for b and d, and O₀ = 5 for c. Blue dots in top panels a–c represents numerical results from late-time optimization of n = 5 qubit RPA. Red solid lines represent exact ensemble average with restricted Haar ensemble in Supplementary Equations (256), (313), (279) in Supplementary Note 12. Magenta dashed lines represent asymptotic ensemble average with restricted Haar ensemble in Eq. (35), (36), (37) which overlap with the exact results (red solid). The observable in all cases is $\left\vert \Phi \right\rangle \left\langle \Phi \right\vert$ with $\left\vert \Phi \right\rangle$ being a fixed Haar random state. In the inset of b, we fix L = 512. In bottom panel, we plot (e) fluctuation ${{{\rm{SD}}}}[{K}_{0}]/\overline{{K}_{0}}$ versus L, (f) $\overline{{\zeta }_{0}}$ versus L, $\overline{{\lambda }_{0}}$ versus (g) L and (h) n with L = 128 under random initialization. Green dots in bottom panel from e–g represent numerical results from random initializations of n = 6 qubit RPA. Brown solid lines represent the exact ensemble average with the Haar ensemble in Supplementary Equations (241), (180), (120) in Supplementary Note 11. Gray dashed lines represent asymptotic ensemble average with a restricted Haar ensemble in Eqs. (45), (39), (40). The observable and target in e–h are XXZ model with J = 2 and ${O}_{0}={O}_{\min }$. Orange solid line in e represents results from ref. ²⁹.

Subplot (a) plots $\overline{{K}_{\infty }}$ versus O₀. At late time, if the target O₀ ≥ 1, from O₀ = 1 + R we directly have $\overline{{K}_{\infty }}=0$; if O₀ < 1, we have R = 0 and $\overline{{K}_{\infty }}\propto {O}_{0}(1-{O}_{0})$ being a constant.

Subplot (b) shows the agreement of $\overline{{\zeta }_{\infty }}$ versus L, when we fix O₀ = 1. As predicted by the theory of Eq. (36), as R = 0 in this case, $\overline{{\zeta }_{\infty }}=1/2$ when L ≫ 1. Indeed, we see convergence towards 1/2 as the depth increases. We also verify the $\overline{{\zeta }_{\infty }}$ versus O₀ relation in the inset, where $\overline{{\zeta }_{\infty }}=0$ for O₀ < 1, 1/2 for O₀ = 1 and diverges for O₀ > 1. Note that for a circuit with medium depth L ∼ poly(n), $\overline{{\zeta }_{\infty }}=1/2+d/L$ would slightly deviate from 1/2 for O₀ = 1 (Fig. 9(b)). This indicates a ‘finite-size’ effect affecting the dynamical transition, which we defer to future work.

Subplot (c) shows the agreement of $\overline{{\lambda }_{\infty }}$ versus L, where the linear relation is verified. As predicted by Eq. (37), this is the case regardless of O₀ value. We also verify the dependence of $\overline{{\lambda }_{\infty }}$ on n (thus d = 2ⁿ) with a fixed L in subplot (d), where we see as n increases, $\overline{{\lambda }_{\infty }}$ converges to a constant only relying on O₀.

Haar ensemble results

We also evaluate the Haar ensemble expectation values for reference, which captures the early-time QNN dynamics. Under the Haar random assumption, we find the following lemma.

Lemma 4

For traceless operator $\hat{O}$, when the initial circuit satisfies Haar random (4-design) and circuit L ≫ 1 and d ≫ 1, the ensemble averages of QNTK, relative dQNTK and dynamical index have leading order

$$\overline{{K}_{0}}= L\frac{d \, {{{\rm{tr}}}}\left({\hat{O}}^{2}\right)}{2(d-1){(d+1)}^{2}},\\ \overline{{\zeta }_{0}}= -\frac{1}{L}\left[1+\frac{{{{\rm{tr}}}}\left({\hat{O}}^{4}\right)}{{{{\rm{tr}}}}{\left({\hat{O}}^{2}\right)}^{2}}\right]$$

(38)

$$+\frac{1}{2}\left[\frac{{{{\rm{tr}}}}\left({\hat{O}}^{4}\right)}{{{{\rm{tr}}}}{\left({\hat{O}}^{2}\right)}^{2}}-d{O}_{0}\frac{{{{\rm{tr}}}}\left({\hat{O}}^{3}\right)}{{{{\rm{tr}}}}{\left({\hat{O}}^{2}\right)}^{2}}-\frac{3}{d}\right],$$

(39)

$$\overline{{\lambda }_{0}}=\frac{L \, {{{\rm{tr}}}}\left({\hat{O}}^{3}\right)}{4d \, {{{\rm{tr}}}}\left({\hat{O}}^{2}\right)}.$$

(40)

Note that for observables with non-zero trace, evaluation is also possible, we present those lengthy formulae and the proofs in Supplementary Note 11. Note that similar to Theorem 3, here the requirement of d ≫ 1 is for simplification of formula only and the full formula in SI applies to any finite d. Meanwhile, it is important to notice the dimension dependence of the trace terms.

Specifically, for the XXZ model we considered, when d ≫ 1, the above Lemma 4 leads to

$${\overline{{K}_{0}}}_{{{{\rm{XXZ}}}}}\simeq \left(1+{J}^{2}\right)\frac{Ln}{d},$$

(41)

$${\overline{{\zeta }_{0}}}_{{{{\rm{XXZ}}}}}\simeq -\frac{1}{L}\left(1+\frac{3}{d}\right)-{O}_{0}\frac{3J(1-{J}^{2})}{4{(1+{J}^{2})}^{2}n},$$

(42)

$${\overline{{\lambda }_{0}}}_{{{{\rm{XXZ}}}}}\simeq \frac{3J(1-{J}^{2})L}{4(1+{J}^{2})d}.$$

(43)

We verified the Haar prediction on $\overline{{\zeta }_{0}}$ and $\overline{{\lambda }_{0}}$ with random initialized circuits in Fig. 9(f)–(h). Note that when L is large enough, ${\overline{{\zeta }_{0}}}_{{{{\rm{XXZ}}}}}$ scales linearly with O₀, while ${\overline{{\lambda }_{0}}}_{{{{\rm{XXZ}}}}}$ converges to zero exponentially with n.

In the Haar case, we can also obtain the fluctuation properties.

Theorem 5

In the asymptotic limit of wide and deep QNN d, L ≫ 1, we have the ensemble average of QNTK standard deviation (4-design)

$${{{\rm{SD}}}}[{K}_{0}]= \left(\frac{3L}{4{d}^{6}}\left[{d}^{2}{{{\rm{tr}}}}{\left({\hat{O}}^{2}\right)}^{2}-2d \, {{{\rm{tr}}}}\left({\hat{O}}^{2}\right){{{\rm{tr}}}}{\left(\hat{O}\right)}^{2}+{{{\rm{tr}}}}{\left(\hat{O}\right)}^{4}\right]\right.\\ {\left.+\frac{{L}^{2}}{4{d}^{5}}\left[d \, {{{\rm{tr}}}}\left({\hat{O}}^{4}\right)-4 \, {{{\rm{tr}}}}\left({\hat{O}}^{3}\right){{{\rm{tr}}}}\left(\hat{O}\right)\right]\right)}^{1/2}.$$

(44)

Note that similar to Theorem 3 and Lemma 4, here the requirement of d ≫ 1 is for simplification of formula only and the full formula in SI applies to any finite d.

For traceless operators, Eq. (44) can be further simplified and the relative sample fluctuation of QNTK is

$$\frac{{{{\rm{SD}}}}[{K}_{0}]}{\overline{{K}_{0}}}=\frac{1}{\sqrt{L}}{\left(L\frac{{{{\rm{tr}}}}\left({\hat{O}}^{4}\right)}{{{{\rm{tr}}}}{\left({\hat{O}}^{2}\right)}^{2}}+3\right)}^{1/2}.$$

(45)

This result refines ref. ²⁹ with a more accurate ensemble averaging technique and provides an additional term $\sim {{{\rm{tr}}}}({\hat{O}}^{4})/{{{\rm{tr}}}}{({\hat{O}}^{2})}^{2}$. Therefore, the sample fluctuation also depends on the observable being optimized. Specifically, for the XXZ model we considered, Eq. (45) becomes

$$\frac{{{{\rm{SD}}}}[{K}_{0}]}{\overline{{K}_{0}}} \, \simeq \, \sqrt{\frac{3}{L}\left(\frac{L}{d}+1\right)}.$$

(46)

When L ≫ d, the relative fluctuation ${{{\rm{SD}}}}[{K}_{0}]/\overline{{K}_{0}} \sim 1/\sqrt{d}$ is constant. However, as d = 2ⁿ is exponential while a realistic number of layers L is polynomial in n, therefore d ≫ L is more common, where the relative fluctuation ${{{\rm{SD}}}}[{K}_{0}]/\overline{{K}_{0}} \sim \sqrt{1/L}$ decays with the depth, consistent with ref. ²⁹. We numerically evaluate the ensemble average in Fig. 9(e) and find a good agreement between our full analytical formula (red solid, Eq. (241) in SI) and the numerical results (blue circle). The asymptotic result (magenta dashed, Eq. (46)) also captures the scaling correctly. The results refine the calculation of ref. ²⁹, which has a substantial deviation when L and d are comparable.