Introduction

The introduction of Kerr nonlinearity in resonators allows for the generation of temporal solitons that are pulses of light traveling in the resonator without any dispersion or dissipation1,2,3,4,5. This dispersion- and dissipation- free propagation is enabled by balancing the linear dispersion of the resonator against the dispersion induced by the Kerr nonlinearity, and the linear resonator losses against the nonlinear gain. In the frequency domain, such temporal solitons lead to the generation of coherent phase-locked optical frequency combs, called Kerr combs, that enable numerous applications, such as on-chip precision clocks, spectroscopy, on-chip microwave synthesis and processing, wavelength multiplexed optical transceivers, and light detection and ranging (LiDARs)5,6,7,8,9,10.

Recently, coupled-resonator systems have emerged as a new paradigm to generate novel soliton states that are not accessible using single resonators11,12,13,14,15,16,17. For example, a photonic molecule, a system of two coupled resonators, has been used to explore the synchronization of solitons11, to engineer dispersion17,18, and also to generate novel soliton states such as gear solitons14. More recently, a two-dimensional (2D) array of coupled ring resonators has demonstrated the use of topological physics to generate a novel class of solitons, called the nested temporal solitons that are associated with nested optical frequency combs19,20. Specifically, this 2D array creates a synthetic magnetic field for photons. This leads to the emergence of topological edge states that circulate the lattice boundary, forming a traveling-wave super-ring resonator. Pumping the edge states generates the nested comb - a set of oscillating edge state resonances, repeating every free-spectral range (FSR) of ring resonators. Within the 2D array, the nested comb is associated with the self-formation of nested temporal solitons - a group of single-ring solitons circulating the edge of the lattice.

Here, we introduce another novel class of topological frequency combs and temporal solitons, the floquet topological solitons that exist in strongly coupled 2D ring resonator arrays. Because of strong coupling, the array exhibits the anomalous floquet topological phase where the edge states emerge even when all the bulk bands have a zero Chern number21,22,23,24. We show that pumping the edge states of this array generates a floquet comb that populates multiple edge bands interleaved by bulk bands. More importantly, this edge-bulk band interleaving leads to the formation of novel incommensurate combs where all the comb lines, corresponding to oscillating edge states, are not equidistant, yet remarkably phase-locked. This is in stark contrast to conventional single or coupled resonator combs where the comb lines are always equidistant. In the spatio-temporal domain, this phase-locked incommensurate comb is associated with the generation of novel super-soliton molecules that are phase-locked across multiple rings and circulate at the edge of the lattice. By tuning the system to another topological phase, the Chern insulator phase, where the bulk bands have non-zero Chern number, we demonstrate another novel floquet topological soliton state where there exists exactly one soliton in every alternating ring on the edge of the lattice, and all the individual solitons are phase-locked forming a large super-soliton molecule. In this state, the output comb spectrum populates only a single edge band and shows oscillation of only a single edge mode in each FSR. We show that these floquet soliton molecules circulating at the edge are robust and they route around defects in the lattice. This routing increases the effective length of the lattice edge, and therefore, allows for post-fabrication agile tunability of the comb line spacing. These results pave the way for further investigations on the use of strongly coupled nonlinear resonator arrays, along with floquet and topological design principles25,26,27,28,29,30,31,32, to tailor dispersion, and thereby, achieve unconventional soliton states and optical frequency combs with engineered spectra.

Results

Our topological photonic system consists of a 2D square lattice of ring resonators (Fig. 1a)21,22,24. The rings are evanescently coupled to their nearest neighbors. The coupling strengths between the resonators depend on their location in the lattice as shown in Fig. 1a, and are parameterized as \({\kappa }_{a}=\sin \left({\theta }_{A}\right)\) and \({\kappa }_{b}=\sin \left({\theta }_{B}\right)\). With this arrangement of coupling strengths, a unit cell of the lattice consists of four resonators. Accordingly, the lattice can host a maximum of four bands. However, the topology of these bands is dictated by the choice of coupling strengths κa and κb. In particular, the lattice exhibits non-trivial topology only when the coupling strength between the resonators is comparable to their FSR. In this regime of strong coupling, the system is referred to as a floquet system because it can not be described using an effective Hamiltonian and the single-mode approximation (close to a single FSR) that is typically used for describing weakly coupled ring resonator systems33,34,35. This resonator system can also be mapped to periodically modulated waveguide arrays implementing a periodically modulated Hamiltonian21,36. Furthermore, depending on the choice of coupling strengths, the lattice can host the anomalous floquet (AF) topological phase or the Chern insulator (CI) phase21,22.

Fig. 1: Floquet soliton combs.
figure 1

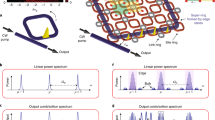
a Schematic of the 2D ring resonator lattice that generates the floquet topological combs. The insets show a unit cell of the lattice (shaded), and the topological phase diagram for different coupling parameters κa, κb. The lattice is coupled to an input-output waveguide that facilitates the injection of a continuous-wave pump and out-coupling of the generated comb. The schematic also shows phase-locked soliton molecules in the lattice and the incommensurate comb spectrum. b, c Transmission (Tx) spectrum and band structure of the lattice for the anomalous floquet (AF) phase at θA = 0.45π, and θB = 0.05π. Edge bands are shaded red. The spectrum repeats every FSR of the ring resonators. The band structure is calculated for a semi-infinite lattice, with k being the momentum and Λ the periodicity of the lattice. d–f Intensity distribution in the lattice for the edge and the bulk states. The bulk state intensity distribution varies significantly with the pump frequency.

Full size image

In the AF phase, which exists, for example, at θA = 0.45π, θB = 0.05π, edge states appear in all band gaps, around normalized frequency detunings \(\delta \omega=\left(\omega -{\omega }_{0}\right) \sim \pm 0.15\,{\Omega }_{R}\) and at δω ~ ± 0.5ΩR (Fig. 1b, c). Here ω is the input light frequency, ω0 is the ring resonance frequency for a given longitudinal mode, and ΩR is the free-spectral range of the rings (in angular frequency units). This topological phase is referred to as the anomalous phase because the edge states appear even though the Chern number for all the bands is zero21,24. Such a topological phase has also been observed in floquet systems implemented using periodically modulated photonic waveguides36. In contrast, in the Chern insulator phase, which exists, for example, at θA = 0.3π, θB = 0.01π, the bulk bands have a non-zero Chern number. As we will discuss in the following, in this phase, the edge states appear in only two of the four bandgaps, around δω ~ ± 0.06ΩR. The array hosts yet another anomalous-floquet phase (the AF-II), for example, at θA = 0.45π, θB = 0.2π where a small band gap supporting edge states appears around δω ~ 0.5ΩR. We did not find any stable soliton solutions in this phase (see Supplementary Discussion 3 and Supplementary Fig. 3).

We emphasize that the band structure and the transmission/absorption spectrum repeat at every longitudinal mode resonance frequency of the ring resonators, spaced by the FSR ΩR (Fig. 1b, c). Furthermore, the topological phases, and the widths of the bulk and the edge bands are dictated by the particular choice of the couplings κa and κb. As we will show in the following, this property allows us to tune the generated comb spectra by tuning the coupling parameters. We also note that because of the strong coupling and the floquet nature of our system, the edge state resonances can appear at frequency detunings \(\delta \omega=\left(\omega -{\omega }_{0}\right)\) that are comparable with the FSR ΩR. In this regime, the usual Lugiato-Lefever formalism that relies on the single-mode approximation for simulating the generation of Kerr combs is no longer valid37,38,39.

To generate optical frequency combs, the lattice is pumped using a continuous-wave laser through an input-output waveguide which is coupled to one of the lattice sites (Fig. 1), with a coupling coefficient κIO. In the lattice, the pump laser generates the optical frequency comb via the four-wave mixing process, and the generated comb appears at the output port of the input-output waveguide. The nonlinear propagation of the fields inside the ring resonators and subsequent generation of combs is simulated using the Ikeda map approach detailed in Methods Section39,40,41. We use dimensionless parameters such that the total ring length LR, the round-trip time τR, and, consequently, the group velocity vg are all set to unity, and the FSR \({\Omega }_{R}=\frac{2\pi }{{\tau }_{R}}=2\pi\). Similarly, the fields are normalized such that the strength of nonlinearity γ is also effectively set to unity. The resonator waveguides are assumed to have a loss coefficient α = 2 × 10−4. To generate bright solitons, we assume that the ring resonators have an anomalous dispersion, given by second-order dispersion parameter D2 which we set to 4 × 10−6ΩR. We emphasize that we do not assume any dispersion profile for the supermodes of the resonator array. The resonance frequencies of the supermodes, which include both the edge and the bulk states, emerge naturally from the simulation framework. Different soliton states are generated by an appropriate choice of the coupling parameters θA, θB, and by tuning the pump frequency and pump power.

Incommensurate combs in the AF phase

To demonstrate the generation of floquet topological solitons, we start with the anomalous floquet phase, implemented in a 9 × 9 lattice of rings with θA = 0.45π, θB = 0.05π. The band structure for a semi-infinite lattice and the corresponding linear power absorption spectrum for the lattice are shown in Fig. 2a, b, respectively, as a function of the normalized pump frequency detuning \(\delta {\omega }_{p}=({\omega }_{p}-{\omega }_{0})\), where ωp is the input pump frequency. The edge states (highlighted in red) manifest as regularly spaced resonances (peaks) in the absorption spectrum. Because the edge states circulate around the complete boundary of the lattice (Fig. 1d), they constitute a super-ring resonator. Therefore, the edge state resonances represent the longitudinal modes of this super-ring resonator. In contrast to the edge states, the bulk mode resonances do not show any regular spatial structure and their wavefunction occupies the bulk of the lattice (Fig. 1e, f).

Fig. 2: Floquet solitons and incommensurate combs in the AF phase, for θA =  0.45π, θB = 0.05π.
figure 2

a Band structure, b absorption spectrum of the lattice, in the linear regime, showing edge and bulk bands. The band structure shown in a. is a zoom-in of Fig. 1c within a single FSR. The absorption spectrum in b. is calculated as (1-Tx), with the transmission (Tx) shown in Fig. 1b, and is zoomed-in within a single FSR. The pumped edge mode is highlighted in blue. c Comb power (normalized) in the input-output ring as a function of pump frequency detuning in the non-linear regime. The pump frequency where we observe coherent incommensurate combs soliton molecules is indicated. d Intensity distribution in the lattice showing phase-locked super-soliton molecules. The super-solitons circulate the edge in the CCW direction as time evolves (here time interval δt = 8τR). Insets show the positions of solitons in the individual rings. To show the location of the rings, we have added a constant intensity (normalized) background of 0.01. e Output of the floquet topological comb in the time domain, showing super-soliton pulses repeating after round trip time in the super-ring resonator. The inset shows a zoom-in of the temporal output where relative intensity variations in the output pulses are clearly visible. f Output comb spectrum. g Comb spectrum reorganized as a function of frequency detuning δω/ΩR and FSR index μ. h Comb spectrum showing oscillation of edge modes in a single FSR (here μ = 50). The incommensurate nature of the comb is evident in g, h where the oscillating edge mode frequencies are not all equidistant.

Full size image

We pump near one of the edge state resonances as shown in Fig. 2b, with normalized pump field Ein = 0.018. The generated comb power in the input-output ring, as a function of the pump frequency, is shown in Fig. 2c. When the input pump frequency detuning δωp = 0.47ΩR, we observe the generation of a floquet super-soliton molecule at the edge of the lattice (Fig. 2d). In this state, three different rings on the edge host a single soliton each. More importantly, we find that the three solitons are always phase-locked, that is, their relative positions in the rings are exactly the same. We refer to this state as a super-soliton molecule. As time evolves, this super-soliton molecule circulates around the edge in the counter-clockwise direction. A movie showing the evolution of this super-soliton molecule is available as Supplementary Movie 1. Furthermore, because of the unique nature of the edge states, neither soliton completes a round-trip in the single ring. This is in contrast to the conventional single-ring solitons, where the soliton is defined as a non-dispersive pulse circulating in the ring resonator. We note that the relative intensities of the three solitons oscillate as a function of time, similar to that observed for breathing solitons in single-ring resonators42. Nevertheless, we have confirmed that the total power in the super-soliton molecule stays constant.

This generation of super-soliton molecules in the lattice manifests at the output port as a repeating set of three pulses (Fig. 2e). The pulses appear at the same relative times τ, indicating that they are phase-locked across all rings. Their repetition rate, equal to  ~ 17τR, corresponds to the round-trip time τSR in the super-ring resonator formed by edge states. Similar to the intensity distributions within the lattice, the relative intensities of the three output pulses show oscillation from one period to the next.

The generated frequency comb spectrum corresponding to this soliton molecule state is shown in Fig. 2f. We observe that the intensity in the comb spectrum is smooth, indicating the existence of a coherent super-soliton state. To better visualize the nature of oscillating modes in the comb, in Fig. 2g, we plot the generated comb spectrum as a function of the longitudinal mode index μ and the normalized frequency detunings \(\delta \omega -\delta {\omega }_{p}=(\omega -{\omega }_{0,\mu })-({\omega }_{p}-{\omega }_{0,0})\). Here ω is the frequency of the generated comb line, and ω0,μ is the resonance frequency for mode μ, with μ = 0 corresponding to the pumped FSR. Therefore, δω − δωp represents frequency detuning within one FSR.

At each longitudinal mode index μ, we observe the oscillation of multiple comb lines, which are indeed the edge state resonances (Fig. 2g, h). More importantly, we find that the oscillating edge state resonances span the complete FSR, encompassing three edge bands (shaded red). Within each edge band, the comb lines are regularly spaced with a frequency spacing ΩSR ≃ 0.056ΩR. However, the adjacent comb lines in neighboring edge bands are spaced by ≃ 0.074ΩR, which is not an integer multiple of ΩSR, the free-spectral range of the super-ring resonator. This clearly shows the generation of an incommensurate floquet topological comb, which is phase-locked even when the constituent comb lines are not equidistant. We note that the periodicity of each oscillating edge mode (comb line) is exactly ΩR, the FSR of the single rings. Therefore, the observed incommensurate combs can be interpreted as sets of several (here 17) combs, each set corresponding to one oscillating edge mode and a line spacing ΩR. Different sets of combs have different frequency offsets (with in ΩR), and therefore, correspond to different carrier-envelope phase. We do not observe any oscillation of the bulk modes in the spectrum, consistent with our observation of negligible intensity in the bulk of the lattice (Fig. 2d).

In Fig. 2f, we also observe the formation of satellite peaks in the incommensurate comb spectrum, similar to those observed in single-ring resonators in the presence of higher-order dispersion which leads to dispersive waves4. From Fig. 2g, we find that these satellite peaks are associated with only two edge modes located at the boundary between the edge and the bulk bands. It is interesting to note that here, we assumed that the higher-order dispersion of the single-ring resonators is zero. Similarly, the edge states are generally assumed to have a linear dispersion in the edge band. However, the band structure in Fig. 2a shows that the edge states do have a non-zero higher-order dispersion near the boundary between the edge and the bulk bands. This higher-order dispersion of edge states generates the satellite peaks.

The anomalous floquet topological combs distinguish themselves from the nested topological combs observed in refs. 19,20 where the oscillating edge state resonances populate a single edge band and are confined to a very close vicinity of the longitudinal mode resonance. Furthermore, unlike incommensurate combs, all the oscillating comb lines are regularly spaced in the nested topological combs.

Commensurate combs in the AF phase

The incommensurate nature of the frequency combs observed here is because of the fact that the edge states participating in the comb formation are inter-spaced by bulk bands. This implies that by tuning the coupling parameters and, thereby, tuning the bulk bandwidth, it should be possible to generate regularly spaced commensurate combs. To show that this is indeed the case, in Fig. 3, we show results for coupling parameters θA = 0.49π, and θB = 0.01π. This choice of coupling parameters still corresponds to the anomalous-floquet (AF) phase, but it significantly reduces the bulk bandwidths and, at the same time, increases the edge bandwidths. At a pump frequency detuning δωp = 0.40994ΩR, we now observe the formation of a single super-soliton in the lattice. In this state, only a single ring at the edge of the lattice hosts a single soliton that circulates the lattice in the counter-clockwise direction (Supplementary Movie 2). Accordingly, the temporal output consists of a single pulse, repeating after the round-trip time τSR ~ 17τR of the super-ring resonator. The frequency comb spectrum, in this case, is regularly spaced and does not exhibit any incommensurate gaps. We also note the absence of satellite peaks in the comb spectrum, which is consistent with the observation of negligible higher-order dispersion of edge states in the band structure, as shown in Fig. 3a. We note that other choices of the coupling parameters in the AF-phase could also yield similar commensurate combs as long as the bulk bandwidth is smaller than the frequency spacing between the edge state resonances.

Fig. 3: Commensurate combs in the AF topological phase, with θA = 0.49π, θB = 0.01π.
figure 3

a, b The band structure and the linear power absorption spectrum of the lattice show reduced bulk bandwidths. c Comb power (normalized) in the input-output as a function of pump frequency. d Intensity distributions in the lattice, at time instances separated by δt = 8τR, show the generation of a single super-soliton in the lattice that circulates the edge in a counter-clockwise direction. e Comb output in the time domain shows the generation of a single pulse, repeating every τSR. The inset shows a zoom-in of the temporal output. f–h Comb output in the frequency domain shows a regular comb with all edge modes oscillating and no incommensurate gaps.

Full size image

We emphasize that pumping the edge state resonances does not guarantee the formation of phase-locked solitons and coherent frequency combs. For example, pumping the edge states with a pump frequency of δωp = 0.4706ΩR generates a comb operating in the modulation instability (chaotic) regime (see Supplementary Discussion 1 and Supplementary Fig. 1). Even though this chaotic comb shows oscillation of multiple edge state resonances, the resonances are not phase-locked, and the resulting comb spectrum is not smooth.

Soliton molecules in the CI phase

Next, we demonstrate the formation of another novel floquet soliton state in the Chern insulator phase (Fig. 4). This phase exhibits three bulk bands, two of which are topologically non-trivial, that is, they have a non-zero Chern number \(\left(-1,0,1\right)\)21. The three bulk bands sandwich two edge bands (Fig. 4a, b). When we tune the pump frequency near one of the edge state resonances, at δωp = 0.0964ΩR, and adjust the normalized input pump field Ein = 0.025, we observe the generation of a completely different soliton molecule state in the lattice: alternate rings on the edge host exactly one soliton, except for the rings on the corners that always host solitons (Fig. 4d). Furthermore, the positions of the solitons in the rings are phase-locked. As time evolves, this intensity distribution appears to be stationary in the lattice (also see Supplementary Movie 3). Similar to the AF phase, the solitons in this phase do not complete a round trip in any single-ring resonator. Nevertheless, the solitons self-organize in alternate rings such that the path length difference between consecutive solitons is exactly equal to the circumference of a single ring resonator.

Fig. 4: Combs in the CI topological phase, with θA = 0.3π, θB = 0.01π.
figure 4

a, b The band structure and the linear power absorption spectrum of the lattice show two edge bands and three bulk bands. c Pump power in the input-output ring as a function of pump frequency. d Intensity distributions in the lattice, at time instances separated by δt = 8τR, show the generation of a single soliton in each alternating ring at the edge of the lattice. This soliton molecule state appears stationary in the lattice. e Comb output in the time domain shows pulses repeating every τR. f–h Comb output in the frequency domain shows oscillation of only a single edge mode (the pumped mode).

Full size image

The output temporal profile, in this case, consists of a series of pulses repeating at τR, the round-trip time of a single ring resonator (Fig. 4e). This behavior is consistent with the observation of soliton pulses in alternating rings such that their path-length difference equals a single resonator’s circumference. We also note that this behavior is completely distinct from that observed in the AF phase, where a set of pulses repeats after the round-trip time τSR in the super-resonator (Fig. 3e). In the frequency domain, we now observe the oscillation of only a single edge state resonance corresponding to the pumped mode (Fig. 4f–h). This observation is consistent with the observation of stationary intensity profile in the lattice (Fig. 4d).

This reduction in the number of oscillating edge modes is most likely due to the decrease in the topological edge bandwidth which decreases the number of edge state resonances and also increases the effective higher-order dispersion from the band edges. We also note the absence of any satellite peaks in the spectrum despite the edge states showing higher-order dispersion near the band edges (Fig. 4a). This is because the oscillation of a single edge mode renders their dispersion irrelevant. Increasing the size of the lattice and thereby, increasing the number of edge state resonances in a given edge band could lead to the oscillation of multiple edge states resonances in the comb spectrum.

It is instructive to compare the formation of this soliton molecule state in the CI phase to the formation of Turing rolls (see Supplementary Discussion 2 and Supplementary Fig. 2). In the case of Turing rolls, we observe the formation of many pulses in each ring. In comparison, for the CI soliton molecules, there is only one pulse in each alternating ring. In both cases, only one edge mode oscillates in the comb spectrum. However, for Turing rolls, this oscillation is confined only to a few FSRs, whereas, for the CI soliton, a single edge mode oscillates in each FSR of the rings.

Robustness and tunability of floquet combs

The hallmark of topological edge states is their robustness against defects and disorders. To demonstrate that the floquet topological solitons and combs inherit this robustness even in the presence of such strong nonlinearity, in Fig. 5, we show the formation of a single soliton in a defected 2D lattice where a ring resonator has been deliberately omitted. For this lattice, we chose the AF phase with θA = 0.49, and θB = 0.01 to generate commensurate combs. We observe that the soliton follows a path that coincides with the edge states in the defected lattice (Fig. 5a). More importantly, we find that the soliton is robust, circulating around the defect without any back-scattering or loosing its coherence Fig. 5d–g (also see Supplementary Movie 4).

Fig. 5: Robustness of edge states and tunability of comb line spacing.
figure 5

a Routing of edge states around a defect in the lattice (in the linear regime). b Generated comb spectrum, and c a zoom-in within a single FSR showing individual comb lines. d–g Routing of solitons around the defect without any scattering or loss of coherence.

Full size image

Interestingly, robust routing around the defect increases the effective length of the edge states. This leads to a concomitant decrease in the comb line spacing (Fig. 5b, c). Specifically, without the defect, the comb line spacing for the commensurate comb was 0.058 ΩR (Fig. 3h). With the defect, the line spacing has reduced to 0.052 ΩR, a change of ~ 10%. Introducing additional defects on the edge would further decrease the comb line spacing. We note that such defects can be dynamically introduced in the lattice by, for example, integrating thermal heaters on the ring resonators that use thermo-optic effect to detune the ring resonance frequencies43. Therefore, the robustness of the edge states provides a convenient route for post-fabrication agile tuning of the comb line spacing. Such tuning is not accessible using single-resonator Kerr combs.

Discussion

We have theoretically demonstrated the existence of a new class of floquet topological dissipative Kerr solitons and coherent combs in strongly coupled ring resonator arrays. In particular, the incommensurate combs observed here go far beyond the conventional definition of frequency combs as a set of equidistant frequencies. Such combs could enable unique functionalities that are not accessible to conventional frequency combs and could necessitate a reassessment of their applications. Our demonstration builds on the now mature, coupled ring resonator platform that has enabled, for example, the observation of topological edge states of light22,34, their robustness against fabrication imperfections44, observation of higher-order corner states45, implementation of topological lasers46, quantum light sources47,48,49,50, and non-Hermitian light steering51. The range of parameters, such as the loss, dispersion, coupling ratios, etc., used for our simulations is consistent with that used typically for single-resonator Kerr combs and can be achieved using the commercial low-loss silicon-nitride platform (see SI Section I). These floquet topological soliton combs augment the recently observed topological nested combs that operate in the weak coupling regime19,20.

On a fundamental level, the floquet topological solitons observed here are temporal counterparts of floquet topological spatial solitons that have been recently observed in coupled waveguide arrays52,53,54. Therefore, our demonstration could pave the way for further exploring intriguing physics at the intersection of optical nonlinearity, topology, and synthetic dimensions and realizing, for example, a temporal analog of the quantized topological pumping of spatial solitons28,55,56,57,58.

Methods

We use the Ikeda map approach to simulate the nonlinear propagation of optical fields and subsequent generation of frequency combs in the ring resonator array. The Ikeda map equations describing the propagation of fields in the resonators, away from coupling regions, are written as39,40,41

$$\frac{d{E}_{x,y}^{m}(z,\mu )}{dz}= i\frac{2\pi }{{L}_{R}{\Omega }_{R}}\left({\omega }_{p}+{\Omega }_{R}\mu -{\omega }_{0\mu }\right){E}_{x,y}^{m}\left(z,\mu \right) \\ -\frac{\alpha }{2}{E}_{x,y}^{m}\left(z,\mu \right)+i\gamma \frac{1}{{\tau }_{R}}\int_{0}^{{\tau }_{R}}d\tau {\left\vert {E}_{x,y}^{m}\left(z,\tau \right)\right\vert }^{2}{E}_{x,y}^{m}\left(z,\tau \right){e}^{i{\omega }_{\mu }\tau }.$$
(1)

Here \({E}_{x,y}^{m}\left(z,\tau \right)\) is the field in a resonator at location \(\left(x,y\right)\) in the lattice, at position z along the resonator waveguide, and at time \(\tau=\left\{0,{\tau }_{R}\right\}\), with τR being the round-trip time in the ring. Its Fourier transform \({E}_{x,y}^{m}\left(z,\mu \right)\) is the field in the frequency domain with μ indicating the corresponding longitudinal mode index. The subscript m labels the round-trip number. α is the propagation loss. The dispersion of the ring resonators is included in their resonance frequencies for a given FSR, indexed by μ, as

$${\omega }_{0,\mu }={\omega }_{0}+{\Omega }_{R}\,\mu+\frac{{D}_{2}}{2}{\mu }^{2},$$
(2)

where \({\Omega }_{R}=2\pi \frac{{v}_{g}}{{L}_{R}}\) is the free spectral range (in angular frequency units), LR is the length of the ring resonator, and D2 is the second-order dispersion which we assume to be anomalous. γ = 2ϵ0n0n2ω0 is the strength of Kerr nonlinearity59. In this form of the equation, linear evolution is described in the frequency domain and nonlinear evolution is described in the time domain, which permits using a split-step process for its numerical solution.

To further simplify the above equation, we use dimensionless parameters and normalized coordinates such that \(z\,\to \,\frac{z}{{L}_{R}}=\left\{0,1\right\}\). Similarly, \(\tau \,\to \,\frac{\tau }{{\tau }_{R}}=\left\{0,1\right\}\). This also implies that the dimensionless FSR ΩR = 2π, and the group velocity vg = 1. The dimensionless fields are then scaled as \({E}_{x,y}^{m}\left(z,\tau \right)\,\to \,\sqrt{\gamma \,L}{E}_{x,y}^{m}\left(z,\tau \right)\) which effectively sets the strength of Kerr nonlinearity γ = 1. Using these dimensionless parameters, the simplified propagation equation is written as

$$\frac{d{E}_{x,y}^{m}(z,\mu )}{dz}= i\left({\omega }_{p}-{\omega }_{0}-\frac{{D}_{2}}{2}{\mu }^{2}\right){E}_{x,y}^{m}\left(z,\mu \right)\\ -\frac{\alpha }{2}{E}_{x,y}^{m}\left(z,\mu \right)+i\int_{0}^{1}d\tau {\left\vert {E}_{x,y}^{m}\left(z,\tau \right)\right\vert }^{2}{E}_{x,y}^{m}\left(z,\tau \right){e}^{i{\omega }_{\mu }\tau }.$$
(3)

Note that this equation is written in a frame moving at velocity vg in the ring resonators and features no dependence on ΩR. Therefore, a soliton pulse, moving at velocity vg, would appear stationary.

The couplings between the rings are described using 2 × 2 beam-splitter transformation matrices of the form

$$\left(\begin{array}{c}{E}_{x,y}^{m}\left({z}_{c},\tau \right)\\ {E}_{{x}^{{\prime} },{y}^{{\prime} }}^{m}\left({z}_{c},\tau \right)\end{array}\right)=\left(\begin{array}{cc}t&i\kappa \\ i\kappa &t\end{array}\right)\left(\begin{array}{c}{E}_{x,y}^{m}\left({z}_{c},\tau \right)\\ {E}_{{x}^{{\prime} },{y}^{{\prime} }}^{m}\left({z}_{c},\tau \right)\end{array}\right).$$
(4)

Here \(t=\sqrt{1-{\kappa }^{2}}\), \(\kappa=\left(\kappa a,{\kappa }_{b}\right)\) is the coupling coefficient between rings indexed by \(\left(x,y\right)\) and its nearest neighbor \(\left({x}^{{\prime} },{y}^{{\prime} }\right)\), at coupling location indicated by zc. The coupling of the input-output waveguide to the lattice at location \(\left(x,y\right)=\left(1,1\right)\) is similarly described, using coupling coefficient κIO, such that

$${E}_{out}^{m}\left(\tau \right)=i{\kappa }_{IO}\,{E}_{1,1}^{m}\left(z=1,\tau \right)+{t}_{IO}{E}_{in}\left(\tau \right).$$
(5)

Here, \({E}_{in}\left(\tau \right)\) is the input pump field, and \({E}_{out}^{m}\left(\tau \right)\) is the output field, at the mth iteration and at time τ. This field yields the temporal output of the generated frequency comb at any time \(t=\left(m-1\right){\tau }_{R}+\tau\), and its Fourier transform yields the frequency spectrum \({E}_{out}\left(\omega \right)\).

For our simulations, we chose α  = 2 × 10−4, \({D}_{2}/\left(2\pi \right)=4\times 1{0}^{-6}\), tIO = 0.985 for combs in the anomalous floquet phase, tIO = 0.995 for solitons in the CI phase, and tIO = 0.975 for Turing rolls in the CI phase. The couplings κ are site-dependent and are chosen to implement a given topological phase. For a ring resonator, with an FSR \({\Omega }_{R}/\left(2\pi \right)=250\,{{{\rm{GHz}}}}\), the dispersion \({D}_{2}/\left(2\pi \right)=1\,{{{\rm{MHz}}}}\) and the intrinsic loss rate \({\kappa }_{in}/\left(2\pi \right)=25\,{{{\rm{MHz}}}}\) which corresponds to an intrinsic quality factor Qi ~ 8 × 106. This range of parameters is experimentally accessible using low-loss photonic platforms such as silicon-nitride14. For this choice of parameters and the normalized input pump field Ein = 0.018 at which we observe soliton molecules in the AF phase, the pump power required to generate incommensurate soliton combs \(P=\frac{c}{{n}_{2}{\omega }_{0}{L}_{R}}{A}_{eff}{\left\vert {E}_{in}\right\vert }^{2} \sim 0.6\,W\), which is also typical for generating Kerr combs.