Experimental realization of on-chip few-photon control around exceptional points

Abstract

Non-Hermitian physical systems have attracted considerable attention in recent years for their unique properties around exceptional points (EPs), where the eigenvalues and eigenstates of the system coalesce. Phase transitions near exceptional points can lead to various interesting phenomena, such as unidirectional wave transmission. However, most of those studies are in the classical regime and whether these properties can be maintained in the quantum regime is still a subject of ongoing studies. Using a non-Hermitian on-chip superconducting quantum circuit, here we observe a phase transition and the corresponding exceptional point between the two phases. Furthermore, we demonstrate that unidirectional microwave transmission can be achieved even in the few-photon regime within the broken symmetry phase. This result holds some potential applications, such as on-chip few-photon microwave isolators. Our study reveals the possibility of exploring the fundamental physics and practical quantum devices with non-Hermitian systems based on superconducting quantum circuits.

Introduction

Non-Hermitian physical systems with exceptional points^1,2,3,4,5 (EPs) have attracted considerable attention in recent years. The coalescence of eigenvalues and eigenstates of the non-Hermitian Hamiltonian around EPs leads to various interesting properties and numerous applications, such as unidirectional transmission and invisibility^{6,7,8,9,10,11,12}, chiral behavior¹³, control of lasers^14,15,16,17 or electromagnetic waves¹⁸, high-precision sensors^19,20,21,22, and topological energy transfer^3,23. While non-Hermitian physics has been studied extensively in classical systems, the quantum behavior of non-Hermitian systems is not fully understood and there is still much to be explored in the quantum realm. Although there has been interesting work to mimic gain-loss-balance mechanisms in two-level systems (e.g., superconducting quantum circuits^24,25, nitrogen-vacancy centers in diamonds²⁶ and trapped ions²⁷), various interesting problems related to quantum non-Hermitian systems in the few-photon regime are still left open^28,29. One interesting topic is unidirectional control of light in the few-photon regime for non-Hermitian systems. Such kinds of quantum nonreciprocal effects are very helpful for constructing quantum devices³⁰, such as quantum diodes³¹ and quantum circulators³², which are key components for quantum information processing. Although it is well known that non-reciprocal wave propagations can be achieved by breaking the symmetries of non-Hermitian physical systems in the vicinity of the exception point, it is challenging to show such kinds of symmetry breaking in the few-photon regime, because the enhanced quantum fluctuations at the exceptional point will disrupt this process.

Demonstrating nonreciprocity in the few-photon regime requires strong nonlinearity, which is quite difficult to achieve in optical systems. This issue could be solved by using superconducting systems, in which strong nonlinearity has been successfully demonstrated at the single-photon level in the microwave frequency regime³³. Superconducting quantum information processing has made great progresses in recent years^34,35,36,37. Highly-efficient widely-tunable on-demand single-photon sources and highly-efficient single-photon detectors in the microwave-frequency regime have been realized in superconducting quantum systems^38,39,40. With the quantum state transfer by a single microwave photon between two superconducting qubits housed in two refrigerators separated apart by 5 meters, it is possible to realize a microwave quantum network and distributed superconducting quantum computing⁴¹. There has been some research on non-Hermitian phenomena in superconducting circuits^42,43,44. However, the control of the transmission of a single microwave photon on a chip is still ongoing research, and is one of the crucial open problems for quantum networks.

In this work, we construct a non-Hermitian system using a superconducting circuit consisting of two cavities and three tunable-gap flux qubits. The two cavities have different decay rates and nearly identical resonance frequencies, with tunability within a range of a few tens of MHz. The effective coupling strength between the cavities can be tuned by a quantum coupler, implemented here as a tunable-gap flux qubit. Using this non-Hermitian system, we observe the phase transitions and the corresponding exceptional points. The qubits introduce additional nonlinearity to the two cavities, enabling the generation of unidirectional microwave transmission. By tuning the effective coupling strength between the cavities and the input photon numbers, we investigate the switchable unidirectional transmission of the system at the few-photon level.

Results

Experimental setup

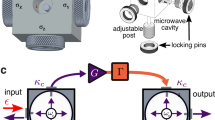
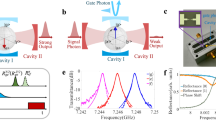
Our experiment is carried out in a dilution refrigerator with a base temperature of about 28 mK. As shown in Fig. 1a–c, the device consists of two superconducting coplanar waveguide (CPW) cavities (marked as Cavity a and Cavity b, respectively) that are capacitively coupled to a tunable-gap flux qubit (working as a quantum coupler and marked as qubit Q_C) with two nominal identical capacitors (see Fig. 1b, c). Tunable coupling between two CPW cavity modes or two CPW cavities based on a flux qubit have been demonstrated^45,46. The Hamiltonian of a qubit coupled to a cavity in the dispersive regime is $H\approx \hslash ({\omega }_{c}+\tilde{\chi }{\sigma }_{z}){a}^{{\dagger} }a+\hslash ({\omega }_{q}+\tilde{\chi }){\sigma }_{z}/2$, where ${\omega }_{c}$ is the cavity frequency, ${\omega }_{q}$ is the qubit transition frequency, $\tilde{\chi }={g}_{0}^{2}/\delta$ is the qubit-state-dependent dispersive cavity shift³³, $\delta=|{\omega }_{q}-{\omega }_{c}|\gg {{{\rm{g}}}}_{0}$, ${g}_{0}$ is the coupling strength between the qubit and the cavity, ${\sigma }_{z}=|0\rangle \langle 0|-|1\rangle \langle 1|$ with the ground $|0\rangle$ and excited $|1\rangle$ states of the qubit, and ${a}^{{\dagger} }$ and $a$ are the creation and annihilation operators of the cavity, respectively. The eigenfrequencies of the two CPW cavities (${\omega }_{a}$ for cavity a and ${\omega }_{b}$ for cavity b, respectively) can be shifted for a few tens of MHz in the dispersive coupling regime, because the cavities are capacitively coupled to other two auxiliary tunable-gap flux qubits (working as cavity frequency shifters and marked as qubit Q_L and qubit Q_R, respectively). Therefore, it is easy to control the detuning frequency between the frequency of the qubit Q_L and the frequency of the cavity a, and that of the qubit Q_R and the cavity b, respectively. In this way, ${\omega }_{a}$ and ${\omega }_{b}$ are tuned to be equal to each other, although the bare eigenfrequencies of the cavities are deviated for few MHz due to the limitation of fabrication. As shown in Fig. 1d, we can apply probing signals through port 1 (port 3) of the left (right) circulator and detect the output signals from port 2 or port 4. It yields four complex elements S_ji of the scattering matrix S, where $i\in \{1,3\}$ and $j\in \{2,4\}$. For example, the normalized S-matrix S₂₁ (S₄₃) is the reflection coefficient of the left (right) cavity, and S₄₁ (S₂₃) is the forward (backward) transmission coefficient. The left cavity (cavity a) supports a high-Q cavity mode $a$ with eigenfrequency ${\omega }_{a}/2\pi \approx 6.474$ GHz and decay rate ${\kappa }_{a}/2\pi \approx 7.7$ MHz, and the right one (cavity b) supports a low-Q cavity mode $b$ with the same eigenfrequency ${\omega }_{b}/2\pi \approx 6.474$ GHz but different decay rate ${\kappa }_{b}/2\pi \approx 20.9$ MHz (see Fig. 1e, f).

Fig. 1: Schematic diagram of the superconducting quantum chip.

a Optical micrograph of the coupling qubit and the two indirectly-coupled coplanar waveguide (CPW) cavities. Two CPW cavities have the same resonant frequency of ${\omega }_{a}/2\pi \approx {\omega }_{b}/2\pi \approx 6.474$ GHz but different decay rates of ${\kappa }_{a}/2\pi=7.7$MHz and ${\kappa }_{b}/2\pi=20.9$ MHz. There are three tunable-gap flux qubits. The left (right) qubit Q_L (Q_R) only couples to the left (right) CPW cavity and works as a cavity frequency shifter to tune the resonant frequency of the left (right) cavity. The central qubit Q_C couples to the two cavities as a quantum coupler to tune the coupling strength between the two cavities. Optical micrograph (b) and scanning electron micrograph (c) of the coupling flux qubit. d Equivalent schematic diagram in which two cavities couple with each other by a quantum coupler. Each cavity is connected to a circulator for extending ports. Reflection spectra of the left high-Q cavity (e) and the right low-Q cavity (f) that display Lorentzian lineshapes detected at low probing power to keep the average photon numbers inside the cavities less than one.

The difference between the decay rates of the two CPW cavities are large enough, such that we can tune the effective coupling strength between the two cavities by changing the transition frequency of the quantum coupler to operate the system in three regimes, i.e., before, after, and in the vicinity of the exceptional point. The coupling flux qubit can be considered as a two-level artificial atom (see Fig. 1d) with transition frequency modulated by the injected external magnetic flux ${\varPhi }_{m}$ in the main loop or ${\varPhi }_{\alpha }$ in the $\alpha$ loop⁴⁵. It works as a quantum coupler to adjust the effective coupling strength between the two cavities (see section 2 of the Supplementary materials). The effective eigenfrequency of the flux qubit is ${\varDelta }_{{{\rm{eff}}}}=\sqrt{{(2{I}_{p}{{\rm{\delta }}}\varPhi )}^{2}+{[\varDelta ({\varPhi }_{\alpha })]}^{2}}$, where ${{\rm{\delta }}}\varPhi\,=\,{\varPhi }_{m}-{\varPhi }_{0}/2$ and ${\varPhi }_{0}$ is the flux quantum, ${I}_{p}$ is the persistent current in the qubit loop, $\varDelta ({\varPhi }_{\alpha })/h\ge$2.0 GHz is the energy gap of the flux qubit which can be turned up by ${\varPhi }_{\alpha }$. By adiabatically eliminating the degree of freedom of the coupling flux qubit, the effective coupling strength between the two cavities is $g=(2{\varDelta }_{q}{g}_{a}{g}_{b})/({\gamma }_{\perp }^{2}+{\varDelta }_{q}^{2})$, where ${\gamma }_{\perp }$ is the relaxation rate of the qubit, ${\varDelta }_{q}={\varDelta }_{eff}-{\omega }_{a}$ and ${g}_{a}={g}_{b}=71$ ${{\rm{MHz}}}$ are the coupling strength between the cavity a (b) and the coupling qubit, respectively.

Observation of the exceptional point

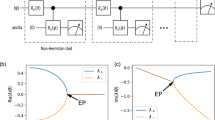
As shown in Fig. 2, the two cavity modes $a$ and $b$ generate two supermodes ${a}_{\pm }$ with complex eigenfrequencies ${\omega }_{\pm }\approx {\omega }_{0}-g-i\chi \pm \beta$, where ${\omega }_{a}={\omega }_{b}={\omega }_{0}$, $\chi=({\kappa }_{a}+{\kappa }_{b})/4$, $\beta=\sqrt{{g}^{2}-{\kappa }^{2}}$, and $\kappa=({\kappa }_{b}-{\kappa }_{a})/4$. The point $g=\kappa$ corresponds to an EP at which both the eigenvalues and the eigenvectors coalesce. The applied probing power $P$ is sufficiently low to keep the average photon numbers $\langle {n}_{i}\rangle=P/\hslash {\omega }_{i}{\kappa }_{i}$ ($i=a,b$) inside the cavity less than one. It can be calibrated by the ac-Stark shift, which is the transition frequency shift of the qubit depending on $\langle {n}_{a}\rangle$, i.e., $\varDelta {\omega }_{L}=2\langle {n}_{a}\rangle {g}_{a}^{2}/\delta$ (see section 1 of the Supplementary materials). After fitting the normalized reflection spectra (${|{S}_{21}|}^{2}$ or ${|{S}_{43}|}^{2}$) with the Lorentzian curves, we obtain the resonance frequencies (the real parts of) and the decay rates (the imaginary parts of) of the supermodes. As shown in Fig. 2a, b, in the strong-coupling regime $g > \kappa$, the two supermodes ${a}_{\pm }$ have the same damping rate $2\chi$ but different resonance frequencies ${\omega }_{0}-g\pm \beta$. The additional frequency shift from ${\omega }_{0}$ to ${\omega }_{0}-g$ for supermodes is induced by the interaction between the quantum coupler (the qubit Q_C) and the cavity modes in the strong dispersive limit, and thus causes the asymmetric frequency evolution in Fig. 2a. In the weak-coupling regime $g\, < \,\kappa$, the resonance frequencies of the two supermodes will be degenerate as ${\omega }_{0}$, while the damping rates of the two supermodes $2\left(\chi\, \mp \,i\beta\right)$ will be different. In our experiments, the damping rate $\kappa$ is kept fixed and the effective coupling strength between the two cavity modes can be tuned by varying the bias flux ${{\rm{\delta }}}\varPhi$ in the main loop of the qubit Q_C, by which we can operate the system in the above three different regimes. Fig. 2c–e show the output spectra of the supermodes in three different regimes, in which the cavity modes $a$ and $b$ have fixed decay rates but different effective coupling strengths $g/\kappa=$ 0.29, 1.04, and 3.11, respectively, where $\kappa=2\pi \times 3.3$MHz. It is shown in Fig. 2d that the supermodes are degenerate in the vicinity of the exceptional point such that $g\approx \kappa$.

Fig. 2: Bifurcation diagram of the supermodes in the vicinity of the exceptional points.

a The real part of the supermodes (frequency). b the imaginary part of the supermodes (decay rate). a, b The blue circles and crosses represent the experimental data and the dashed lines represent the theoretical curves. Normalized reflection spectra from the right low-Q cavity with different coupling strength $g$. (c) Before the exceptional point ($g/\kappa=0.29$) in which two supermodes overlap with each other but with different decay rates. (d) In the vicinity of the exceptional point ($g/\kappa=1.04$) in which two supermodes are degenerate. (e) After the exceptional point ($g/\kappa=3.11$) in which two supermodes are splitting. The applied probing power is low enough to keep $\langle {n}_{a}\rangle \approx 0.06$ with a precision better than ±3 dB inside the high-Q cavity.

Nonreciprocal transmission at the few-photon level

Strong nonlinearity can result in nonreciprocal transmission of photons. In our system, the auxiliary and coupling qubits will induce third-order nonlinear terms to the cavity modes. However, since the frequency detunings between the qubits and cavity modes are large in our experiments, the coefficients of the third-order nonlinear terms are of the order of several kHz when the system is away from EP, and thus is too weak to induce nonreciprocal transmission of photons (see section 3 of the Supplementary materials). Fortunately, in the weak-coupling regime and in the vicinity of EP, the supermodes are localized in the high-Q cavity and thus the nonlinearity of the system is efficiently enhanced. This enhanced nonlinearity enables nonreciprocal transmission of photons in the weak-coupling regime (see Fig. 3c). In fact, in the experiments, we apply probing fields with average photon numbers $\langle {n}_{a}\rangle \approx 3$ inside the high-Q cavity from port 1 (forward with a transmittance T_F) and port 3 (backward with a transmittance T_B) respectively. The backward output field is stronger than the forward one when the effective coupling strength is weak. However, this nonreciprocal effect is suppressed when the effective coupling strength between the two cavities is strong enough to enter the strong-coupling regime (Fig. 3d). We demonstrate the nonreciprocal transmission of photons under different coupling strengths, and the maximum isolation ratio defined as $I=10\,\log ({T}_{B}/{T}_{F})$ can be up to 10.1 dB with $\langle {n}_{a}\rangle \approx 3$ (see Fig. 3a). It is shown in Fig. 3e that the forward output power will increase nonlinearly with the increase of average photon numbers $\langle {n}_{a}\rangle$ in the weak-coupling regime, while it will increase linearly in the strong coupling regime.

Fig. 3: Few-photon nonreciprocity.

a Isolation ratio versus the effective coupling strength $g$ and the detuning frequency between the frequency $\omega$ of the probe field and the frequency ${\omega }_{o}$ of the cavity mode with $\langle {n}_{a}\rangle \approx 3$. b Isolation ratio versus effective coupling strength $g/\kappa$ and the average photon numbers $\langle {n}_{a}\rangle$ inside the cavity with $(\omega -{\omega }_{0})/2\pi \approx 2.7$MHz. c Comparison of forward (blue, $1\to 4$ in Fig. 1a) and backward (red, $3\to 2$ in Fig. 1a) transmission rates in the weak-coupling regime. d Same as c in the strong-coupling regime. The transmission rates in c and d are defined as $10\,\log ({V}_{{{\rm{out}}}}^{2}/{V}_{{{\rm{in}}}}^{2})$ and have been normalized, where ${V}_{{{\rm{in}}}}$ and ${V}_{{{\rm{out}}}}$ are the input and output complex amplitudes of the probing fields. e The forward output power versus the average photon numbers $\langle {n}_{a}\rangle$ with $(\omega -{\omega }_{0})/2\pi \approx 2.7$ MHz. The red circle data are measured with effective coupling strength $g/\kappa \approx 2.70$. The blue triangle data are measured with coupling strength $g/\kappa \approx 0.09$. The sweep direction for a–e is from low frequency to high frequency, from forward to backward, and from low power to high power.

We also study the isolation ratio depending on the average photon number $\langle {n}_{a}\rangle$ inside the high-Q cavity (see Fig. 3b). As we mentioned earlier, the maximum isolation ratio of around 10.1 dB appears in the weak-coupling regime for $\langle {n}_{a}\rangle \approx 3$. In the following analysis, we focus on the variation of this maximum value as a function of $\langle {n}_{a}\rangle$. In Fig. 3b, the isolation ratio decreases when reducing $\langle {n}_{a}\rangle$ and the nonreciprocal transmission phenomenon becomes nearly invisible when we keep $\langle {n}_{a}\rangle\, < \,1.5$. The reason is that the nonlinearity of the cavity modes and the amplification of the nonlinearity induced by the EP phenomenon decrease simultaneously with decreasing $\langle {n}_{a}\rangle$. Due to the strong nonlinearity of the superconducting quantum circuits at few-photon regime, there is still obvious nonreciprocal transmission effect when we keep $\langle {n}_{a}\rangle \approx 2$ (corresponding to the input power less than −122 dBm on chip), which are much smaller than that shown in the classical PT-symmetric system¹¹.

Discussion

We have observed the exceptional points and demonstrated nonreciprocal behavior, i.e., unidirectional transmission of microwave at a few-photon level, in a non-Hermitian superconducting coupled-cavities system with a tunable quantum coupler. When the system is in the weak-coupling regime, the isolation ratio of unidirectional transmission can achieve 10.1 dB, while almost zero isolation ratio is observed in the strong-coupling regime. Our device can be a switchable few-photon isolator by tuning the effective coupling strength between the two coupled-cavities using an external magnetic field. This switchable few-photon isolator has potential applications for the transmission of quantum information.

Methods

The System Hamiltonian

Using Jaynes-Cummings-type description, the total Hamiltonian of the system shown in Fig. 1d is

$${H}_{c}={\omega }_{a}{a}^{{\dagger} }a+{\omega }_{b}{b}^{{\dagger} }b+{\omega }_{q}{\sigma }_{+}{\sigma }_{-}+{g}_{a}({a}^{{\dagger} }{\sigma }_{-}+a{\sigma }_{+})+{g}_{b}({b}^{{\dagger} }{\sigma }_{-}+b{\sigma }_{+})$$

(1)

where ${g}_{a} ({g}_{b})$ is the coupling strength between the cavity mode $a$ ($b$) and the central flux qubit. In our experiment, ${g}_{a}\approx {g}_{b}$. are the resonance frequencies of the two cavities and the central qubit. By applying adiabatic elimination to the central qubit, we obtain the system’s effective Hamiltonian as

$${H}_{eff}=\left({\omega }_{a}-g-\frac{i{\kappa }_{a}}{2}\right){a}^{{\dagger} }a+\left({\omega }_{b}-g-\frac{i{\kappa }_{b}}{2}\right){b}^{{\dagger} }b\\ -g(a{b}^{{\dagger} }+{a}^{{\dagger} }b)+{\mu }_{kerr}({a}^{{\dagger} }a{a}^{{\dagger} }a+{b}^{{\dagger} }b{b}^{{\dagger} }b),$$

(2)

where ${\kappa}_{a} ({\kappa}_{b})$ is the decay rate of cavity mode $a$ ($b$). The effective coupling strength between the two cavity modes $g$ and the effective self-Kerr coefficient ${\mu }_{kerr}$ can be written as

$$g=\frac{{\varDelta }_{q}{g}_{a}{g}_{b}}{{\varDelta }_{q}^{2}+{\gamma }_{\perp }^{2}},\,$$

(3)

$${\mu }_{kerr}=\frac{4{g}_{a(b)}^{4}{\varDelta }_{q}{\gamma }_{\perp }}{{\gamma }_{//}{({\varDelta }_{q}^{2}+{\gamma }_{\perp }^{2})}^{2}}.$$

(4)

Here, ${\varDelta }_{q}={\omega }_{q}-{\omega }_{a}$ and ${\gamma }_{\perp }={\gamma }_{//}/2+{\gamma }_{\varphi }$ is the central qubit’s total relaxation rate formed by its depolarizing rate ${\gamma }_{\parallel }$ and its dephasing rate ${\gamma }_{\varphi }$.

At zero detuning (${\omega }_{a}={\omega }_{b}={\omega }_{0}$), The eigenvalues of linear terms in Eq. (2) are

$${\omega }_{\pm }=\,{\omega }_{0}-g-\frac{i}{4}({\kappa }_{a}+{\kappa }_{b})\pm \sqrt{{g}^{2}-\frac{{({\kappa }_{a}-{\kappa }_{b})}^{2}}{16}}.$$

(5)

It can be shown that there is an exceptional point (EP) at $g=\kappa \equiv |{\kappa }_{a}-{\kappa }_{b}|/4$. The above calculation details can be found in Section 2 of the supplementary materials.

Device fabrication

The superconducting quantum chip is fabricated using a well-established multi-layer thin-film process, featuring a four-layer structure. Electron-beam lithography is employed for the Josephson junction layer, while optical lithography is used for the other layers. The fabrication process begins by depositing a 100 nm aluminum layer on a sapphire substrate, followed by etching the aluminum to form the coplanar waveguide (CPW) cavities and control lines using an aluminum etchant. Next, a 60 nm gold layer is deposited to serve as markers for e-beam alignment. For the Josephson junctions (flux qubit), we use a standard double-angle evaporation process⁴⁷, depositing 40 nm of aluminum at 20° and 60 nm at −20°. Finally, air-bridges are fabricated above the transmission lines and the control lines to minimize crosstalk between them⁴⁸. The primary challenge in this fabrication process lies in the numerous steps involved, where even a single error at any stage can result in the failure of the entire fabrication.

Measurement

We use a four-port vector network analyzer (VNA) to simultaneously measure the reflection spectra and transmission spectra of the system. We can obtain resonant frequencies and decay rates of the two bare cavities through the reflection spectra when the transition frequencies of the qubits are far away from the cavities. We can apply external magnetic field in $\alpha$ loop to make the transition frequency between the ground state and the excited state of the qubit Q_L (Q_R) resonant with the cavity a (cavity b), respectively. As shown in Fig. S2 in the supplementary materials, we scan the normalized amplitudes of the reflection coefficients (|S₂₁| and |S₄₃|) around the resonant frequency of the two cavities as functions of the probing frequency and flux bias δΦ in the main loop of Q_L and Q_R. The phenomena of vacuum Rabi splitting are observed. By fitting the curves of vacuum Rabi splitting, we can obtain the coupling strengths between cavities and the two qubits.